Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Athanassoulis, G. A.
and
Stefanakos, Ch. N.
1995.
A nonstationary stochastic model for long‐term time series of significant wave height.
Journal of Geophysical Research: Oceans,
Vol. 100,
Issue. C8,
p.
16149.
Pelinovsky, E.
Holloway, P. E.
and
Talipova, T.
1995.
A statistical analysis of extreme events in current variations due to internal waves from the Australian North West Shelf.
Journal of Geophysical Research: Oceans,
Vol. 100,
Issue. C12,
p.
24831.
Seleznjev, Oleg
1996.
Large deviations in the piecewise linear approximation of Gaussian processes with stationary increments.
Advances in Applied Probability,
Vol. 28,
Issue. 02,
p.
481.
Albin, J. M. P.
1998.
On extremal theory for self-similar processes.
The Annals of Probability,
Vol. 26,
Issue. 2,
Albin, J.M.P.
1999.
Extremes of totally skewed α-stable processes11Research supported by `Naturvetenskapliga Forskningsrådet Contract F-AA/MA 9207-307, and by Office of Naval Research Grant N00014-93-1-0043..
Stochastic Processes and their Applications,
Vol. 79,
Issue. 2,
p.
185.
Nadarajah, Saralees
2003.
Stochastic Processes: Modelling and Simulation.
Vol. 21,
Issue. ,
p.
607.
Serpedin, Erchin
Panduru, Flaviu
Sarı, Ilkay
and
Giannakis, Georgios B.
2005.
Bibliography on cyclostationarity.
Signal Processing,
Vol. 85,
Issue. 12,
p.
2233.
Gardner, William A.
Napolitano, Antonio
and
Paura, Luigi
2006.
Cyclostationarity: Half a century of research.
Signal Processing,
Vol. 86,
Issue. 4,
p.
639.
Giné, Evarist
and
Nickl, Richard
2010.
Confidence bands in density estimation.
The Annals of Statistics,
Vol. 38,
Issue. 2,
Gong, Zhiyun
Kiessler, Peter
and
Lund, Robert
2011.
A prediction‐residual approach for identifying rare events in periodic time series.
Journal of Time Series Analysis,
Vol. 32,
Issue. 4,
p.
407.
Falk, Michael
Hüsler, Jürg
and
Reiss, Rolf-Dieter
2011.
Laws of Small Numbers: Extremes and Rare Events.
p.
381.
Giné, E.
Güntürk, C. S.
and
Madych, W. R.
2011.
On the Periodized Square ofL2Cardinal Splines.
Experimental Mathematics,
Vol. 20,
Issue. 2,
p.
177.
Tan, Zhongquan
and
Hashorva, Enkelejd
2013.
Limit theorems for extremes of strongly dependent cyclo-stationary χ-processes.
Extremes,
Vol. 16,
Issue. 2,
p.
241.
Tan, Zhongquan
and
Wang, Kaiyong
2015.
On Piterbarg's max-discretisation theorem for homogeneous Gaussian random fields.
Journal of Mathematical Analysis and Applications,
Vol. 429,
Issue. 2,
p.
969.
Bai, Long
2018.
Extremes of Lp-norm of vector-valued Gaussian processes with trend.
Stochastics,
Vol. 90,
Issue. 8,
p.
1111.
Xiao, Jinghong
Wen, Yuechun
and
Tan, Zhongquan
2019.
The limit properties of point processes of upcrossings in nonstationary strongly dependent Gaussian models.
Statistics & Probability Letters,
Vol. 149,
Issue. ,
p.
38.
Napolitano, Antonio
2020.
Cyclostationary Processes and Time Series.
p.
3.
2020.
Cyclostationary Processes and Time Series.
p.
525.
Konakov, Valentin
Panov, Vladimir
and
Piterbarg, Vladimir
2021.
Extremes of a class of non-stationary Gaussian processes and maximal deviation of projection density estimates.
Extremes,
Vol. 24,
Issue. 3,
p.
617.
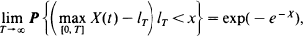 is established for
is established for 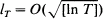 and all x > 0.
and all x > 0.

