Hostname: page-component-5c6d5d7d68-wp2c8 Total loading time: 0 Render date: 2024-08-20T16:32:30.688Z Has data issue: false hasContentIssue false
  • English
  • Français

On the integral of the workload process of the single server queue

Part of: Markov processes Special processes Stochastic processes

Published online by Cambridge University Press:  14 July 2016

A. A. Borovkov ,
O. J. Boxma  and
Z. Palmowski
A. A. Borovkov*
Affiliation:
Sobolev Institute of Mathematics, Novosibirsk
O. J. Boxma*
Affiliation:
EURANDOM and Eindhoven University of Technology
Z. Palmowski*
Affiliation:
EURANDOM and University of Wrocław
*
∗ Postal address: Sobolev Institute of Mathematics, Koptyug pr. 4, Novosibirsk 630090, Russia.
∗∗ Postal address: Eindhoven University of Technology, Department of Mathematics and Computer Science, PO Box 513, 5600 MB Eindhoven, The Netherlands.
∗∗∗ Postal address: Mathematical Institute, University of Wrocław, pl. Grunwaldzki 2/4, 50-384 Wrocław, Poland. Email address: palmowski@eurandom.tue.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is devoted to a study of the integral of the workload process of the single server queue, in particular during one busy period. Firstly, we find asymptotics of the area 𝒜 swept under the workload process W(t) during the busy period when the service time distribution has a regularly varying tail. We also investigate the case of a light-tailed service time distribution. Secondly, we consider the problem of obtaining an explicit expression for the distribution of 𝒜. In the general GI/G/1 case, we use a sequential approximation to find the Laplace—Stieltjes transform of 𝒜. In the M/M/1 case, this transform is obtained explicitly in terms of Whittaker functions. Thirdly, we consider moments of 𝒜 in the GI/G/1 queue. Finally, we show asymptotic normality of .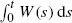

Keywords

Workload processarearegularly varying distributionsequential approximationcovariance function

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Secondary: 60J60: Diffusion processes 60J65: Brownian motion 60K25: Queueing theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 40 , Issue 1 , March 2003 , pp. 200 - 225
Copyright
Copyright © Applied Probability Trust 2003 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Work supported by KBN under grant 5 P03A 02120

References

[1] Abate, J., and Whitt, W. (1994). Transient behavior of the M/G/1 workload process. Operat. Res. 42, 750–764.Google Scholar
[2] Abramowitz, M., and Stegun, I. A. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. John Wiley, New York.Google Scholar
[3] Asmussen, S. (1982). Conditioned limit theorems relating a random walk to its associate, with applications to risk reserve processes and the GI/G/1 queue. Adv. Appl. Prob. 14, 143–170.Google Scholar
[4] Asmussen, S. (1987). Applied Probability and Queues. John Wiley, New York.Google Scholar
[5] Asmussen, S. (1997). Subexponential asymptotics for stochastic processes: extremal behaviour, stationary distributions and first passage times. Ann. Appl. Prob. 8, 354–374.Google Scholar
[6] Asmussen, S. and Möller, J. (1999). Tail asymptotics for M/G/1 type queueing processes with subexponential increments. Queueing Systems 33, 153–176.CrossRefGoogle Scholar
[7] Bartfai, P. (1970). Limes superior Sätze für die Wartemodelle. Studia Sci. Math. Hung. 5, 317–325.Google Scholar
[8] Beneŝ, V., (1957). On queues with Poisson arrivals. Ann. Math. Statist. 28, 670–677.Google Scholar
[9] Bingham, N. H., Goldie, C. M., and Teugels, J. L. (1987). Regular Variation. Cambridge University Press.CrossRefGoogle Scholar
[10] Borovkov, A. A. (1998). Ergodicity and Stability of Stochastic Processes. John Wiley, Chichester.Google Scholar
[11] Borovkov, A. A. (2001). On large deviations for the first crossing time. Preprint No 85, Sobolev Institute of Mathematics, Novosibirsk.Google Scholar
[12] Cohen, J. W. (1976). On Regenerative Processes in Queueing Theory (Lecture Notes Econom. Math. 121). Springer, Berlin.Google Scholar
[13] Cohen, J. W. (1978). Properties of the process of level crossings during a busy cycle of the M/G/1 queueing system. Math. Operat. Res. 3, 133–144.CrossRefGoogle Scholar
[14] Embrechts, P., and Schmidli, H. (1994). Ruin estimation for a general insurance risk model. Adv. Appl. Prob. 26, 404–422.Google Scholar
[15] Feller, W. (1971). An Introduction to Probability Theory and Its Applications, Vol. 2, 2nd edn. John Wiley, New York.Google Scholar
[16] Gerber, H. U. (1971). Der Einfluss von Zins auf die Ruinwahrscheinlichkeit. Schweiz. Verein. Versicherungsmath. Mitt. 71, 63–70.Google Scholar
[17] Greiner, M., Jobmann, M. and Klüppelberg, C. (1999). Telecommunication traffic, queueing models, and subexponential distributions. Queueing Systems 33, 125–152.Google Scholar
[18] Gut, A. (1988). Stopped Random Walks. Limit Theorems and Applications. Springer, New York.Google Scholar
[19] Gut, A. (1997). Stopped two-dimensional perturbed random walks and Lévy processes. Statist. Prob. Lett. 35, 317–325.Google Scholar
[20] Heath, D., Resnick, S., and Samorodnitsky, G. (1997). Patterns of buffer overflow in a class of queues with long memory in the input stream. Ann. Appl. Prob. 7, 1021–1057.Google Scholar
[21] Heath, D., Resnick, S., and Samorodnitsky, G. (1998). Heavy tails and long range dependence in ON/OFF processes and associated fluid models. Math. Operat. Res. 23, 145–165.Google Scholar
[22] Iglehart, D. L. (1971). Functional limit theorems for the queue GI/G/1 in light traffic. Adv. Appl. Prob. 3, 269–281.Google Scholar
[23] Iglehart, D. L. (1972). Extreme values in the GI/G/1 queue. Ann. Math. Statist. 43, 627–635.CrossRefGoogle Scholar
[24] Kelly, F. P. (1991). Effective bandwidths at multi-class queues. Queueing Systems 9, 5–16.Google Scholar
[25] Kingman, J. F. C. (1970). Inequalities in the theory of queues. J. R. Statist. Soc. B 32, 102–110.Google Scholar
[26] Miller, H. D. (1961). A convexity property in the theory of random variables defined on a finite Markov chain. Ann. Math. Statist. 32, 1260–1276.Google Scholar
[27] Ott, T. J. (1977). The covariance function of the virtual waiting time process in an M/G/1 queue. Adv. Appl. Prob. 9, 158–168.Google Scholar
[28] Palmowski, Z., and Rolski, T. (2002). A technique of exponential change of measure for Markov processes. Submitted. Bernoulli 8, 767–785.Google Scholar
[29] Pitman, E. J. G. (1980). Subexponential distribution functions. J. Austral. Math. Soc. A 29, 337–347.Google Scholar
[30] Ross, S. M. (1974). Bounds on the delay distribution in GI/G/1 queues. J. Appl. Prob. 11, 417–421.Google Scholar
[31] Takács, L. (1962). Introduction to The Theory of Queues. Oxford University Press.Google Scholar
[32] Zwart, A. P. (2001). Queueing Systems with Heavy Tails. Doctoral Thesis, Eindhoven University of Technology.Google Scholar