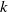1. Introduction
A k-out-of-n system with n components functions if at least k components work. Parallel and series systems are particular cases of such systems corresponding to
![]() $k=1$
and
$k=1$
and
![]() $k=n$
, respectively. These systems play an important role in reliability theory and life testing with several practical applications. The lifetime of such a system is described by the
$k=n$
, respectively. These systems play an important role in reliability theory and life testing with several practical applications. The lifetime of such a system is described by the
![]() $(n-k+1)$
th-order statistic in a sample of size n (or the corresponding ordered component lifetime). For many years, different properties of such systems have been studied assuming that the lifetimes of the components are independent and identically distributed (i.i.d.) and continuously distributed. For thorough details of these concepts, we refer the readers to [Reference Barlow and Proschan5], [Reference Lindqvist, Samaniego and Huseby17], [Reference Marshall and Olkin18], [Reference Navarro20], [Reference Shaked and Shanthikumar26] and the references therein.
$(n-k+1)$
th-order statistic in a sample of size n (or the corresponding ordered component lifetime). For many years, different properties of such systems have been studied assuming that the lifetimes of the components are independent and identically distributed (i.i.d.) and continuously distributed. For thorough details of these concepts, we refer the readers to [Reference Barlow and Proschan5], [Reference Lindqvist, Samaniego and Huseby17], [Reference Marshall and Olkin18], [Reference Navarro20], [Reference Shaked and Shanthikumar26] and the references therein.
It is well known that the monotonicity property for the failure (or hazard) rate function of a life distribution plays an important role in modeling failure time data since it describes the ageing process. Therefore the identification and properties of increasing failure rate (IFR) and decreasing failure rate (DFR) distributions have been extensively studied in the literature. In the continuous case, the IFR property is equivalent to possessing ordered residual lifetimes, in which the residual lifetime of a younger used unit is more reliable than the residual lifetime of any older one. Hence the preservation of this natural property in systems is to be expected. The preservation of the IFR ageing class under the formation of k-out-of-n systems with i.i.d. components with a common absolutely continuous distribution function can be traced back to the 1963 paper by Esary and Proschan [Reference Esary and Proschan9]. However, the DFR class is not preserved except in the case of series systems (see [Reference Navarro20, p. 122]).
The preservation of the IFR class in k-out-of-n systems with i.i.d. components cannot be extended to coherent systems with different structures. In the i.i.d. continuous case, this preservation will depend on the structure of the system. In this sense, a sufficient condition for that preservation based on the signature of the system was obtained by Samaniego [Reference Samaniego25]. More recently, a necessary and sufficient condition was obtained in [Reference Navarro, del Águila, Sordo and Suárez-Llorens21] (see also Theorem 4.1 of [Reference Navarro20]). Surprisingly, there exist coherent systems with i.i.d. components that do not preserve the IFR property (see e.g. Example 4.1 of [Reference Navarro20]). The condition provided in [Reference Navarro, del Águila, Sordo and Suárez-Llorens21] can also be applied to systems with dependent and identically distributed (i.d.) component lifetimes. In this case, the preservation will also depend on the copula that describes the dependence between the component lifetimes.
As the IFR property was not preserved in all the coherent systems with i.i.d. components, another ageing class was considered, the new better than used (NBU) property, which just assumes that new units are always more reliable than used units (of any age). In this sense Esary et al. [Reference Esary, Marshall and Proschan10] (see also [Reference Barlow and Proschan5, p. 85] or [Reference Navarro20, p. 131]) proved that the NBU ageing class is preserved in all the coherent systems with independent components. The same holds for the class of increasing failure rate average (IFRA) distributions. Also, Block and Savits [Reference Block and Savits6] proved that the IFRA class is closed under convolution. Another relevant ageing class is the decreasing mean residual life (DMRL) property. Abouammoh and El-Neweihi [Reference Abouammoh and El-Neweihi1] proved that this class is preserved under the formation of parallel systems with i.i.d. components. This result was extended in [Reference Navarro19] given sufficient conditions for the preservation of DMRL/IMRL classes in systems with i.d. components. Preservation properties for NBUE/NWUE classes can be seen in [Reference Li and Li15] and [Reference Lindqvist and Samaniego16]. Recent preservation results for systems under the exponential distribution were obtained in [Reference Rychlik and Szymkowiak24].
In another direction, discrete failure rates arise in several common situations in reliability theory where clock time is not the best scale to describe lifetimes. For example, in weapons reliability, the number of rounds fixed until failure is more important than the age at the time of failure. However, for the discrete case, the preservation of the IFR and DFR properties is not straightforward because of the complexity of the discrete failure rate. Some properties on ageing notions and order statistics in the discrete case can be found in [Reference Alimohammadi, Alamatsaz and Cramer2], [Reference Bracquemond, Gaudoin, Roy and Xie7], [Reference Dembińska8], [Reference Gupta, Gupta and Tripathi11] and [Reference Kemp14].
In the discrete case, Roy and Gupta [Reference Roy and Gupta23] proved that IFRA ageing class is preserved in coherent systems with independent components. This property also holds in the discrete case for the NBU ageing class (see Proposition 4.1 of [Reference Navarro20]). However, the IFR closure property has not yet been proved in the discrete case.
In this article we prove that the IFR class is preserved in k-out-of-n systems with i.i.d. components with a common discrete distribution. The proof is based on a characterization of log-concavity of the function
![]() $f({{\mathrm{e}}}^x)$
. This method motivated us to extend the result to general coherent systems having i.d. components with discrete distributions or with general distributions.
$f({{\mathrm{e}}}^x)$
. This method motivated us to extend the result to general coherent systems having i.d. components with discrete distributions or with general distributions.
The rest of the paper is organized as follows. In Section 2 we include definitions and some preliminary results. The proof for the discrete case is in Section 3. The extension for arbitrary distributions and systems is presented in Section 4.
2. Preliminaries
Throughout the paper, increasing and decreasing mean non-decreasing and non-increasing, respectively. Furthermore, ratios, derivatives, and conditional distributions are assumed to be well-defined whenever they are used.
In this section we review some notions related to our main results (see [Reference Barlow and Proschan5]). First we give the following definition extracted from [Reference An3].
Definition 1. Let
![]() $f\,:\, \mathbb{R} \longmapsto \mathbb{R}_+$
be a Lebesgue-measurable function. Suppose
$f\,:\, \mathbb{R} \longmapsto \mathbb{R}_+$
be a Lebesgue-measurable function. Suppose
The function f is said to be log-concave in (l, u) if
for all
![]() ${x},{y} \in (l,u)$
and
${x},{y} \in (l,u)$
and
![]() $\alpha \in (0,1)$
.
$\alpha \in (0,1)$
.
With this definition, f is log-concave if and only if
![]() $\log f$
is concave. Moreover, it is known (see e.g. [Reference An3]) that if the function f is continuous, then this definition is equivalent to
$\log f$
is concave. Moreover, it is known (see e.g. [Reference An3]) that if the function f is continuous, then this definition is equivalent to
for all
![]() $\delta \geq 0$
and all
$\delta \geq 0$
and all
![]() $l\leq x_1\leq x_2\leq x_2+\delta \leq u$
.
$l\leq x_1\leq x_2\leq x_2+\delta \leq u$
.
Definition 2. Let
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
be subsets of the real line
$\mathcal{Y}$
be subsets of the real line
![]() $\mathbb{R}$
. A function
$\mathbb{R}$
. A function
![]() $f\,:\, \mathcal{X}\times \mathcal{Y}\rightarrow \mathbb{R}$
is said to be totally positive of order 2
$f\,:\, \mathcal{X}\times \mathcal{Y}\rightarrow \mathbb{R}$
is said to be totally positive of order 2
![]() $({\mathrm{TP}}_2)$
if
$({\mathrm{TP}}_2)$
if
for all
![]() $x_1, x_2\in \mathcal{X}$
and all
$x_1, x_2\in \mathcal{X}$
and all
![]() $y_1,y_2\in\mathcal{Y}$
such that
$y_1,y_2\in\mathcal{Y}$
such that
![]() $x_1\leq x_2$
and
$x_1\leq x_2$
and
![]() $y_1\leq y_2$
.
$y_1\leq y_2$
.
In the next lemma we give a useful characterization for log-concavity of the function
![]() $f({{\mathrm{e}}}^x)$
.
$f({{\mathrm{e}}}^x)$
.
Lemma 1. Let
![]() $f\,:\, \mathbb{R}_+ \longmapsto \mathbb{R}_+$
be a Lebesgue-measurable function. Suppose
$f\,:\, \mathbb{R}_+ \longmapsto \mathbb{R}_+$
be a Lebesgue-measurable function. Suppose
Then
![]() $f({{\mathrm{e}}}^x)$
is log-concave in
$f({{\mathrm{e}}}^x)$
is log-concave in
![]() $(\!\log l,\log u)\subseteq \mathbb{R}$
if and only if
$(\!\log l,\log u)\subseteq \mathbb{R}$
if and only if
for all
![]() $\epsilon \geq 1$
and all
$\epsilon \geq 1$
and all
![]() $l\leq x \leq y \leq y \epsilon \leq u$
.
$l\leq x \leq y \leq y \epsilon \leq u$
.
Proof. (Necessity) In [Reference Hu, Nanda, Xie and Zhu12] it is pointed out that
![]() $f({{\mathrm{e}}}^x)$
is log-concave if and only if
$f({{\mathrm{e}}}^x)$
is log-concave if and only if
![]() $f(s/t)$
is
$f(s/t)$
is
![]() ${\mathrm{TP}}_2$
in
${\mathrm{TP}}_2$
in
![]() $(s,t)\in \mathbb{R}_+\times \mathbb{R}_+$
. So, from (2),
$(s,t)\in \mathbb{R}_+\times \mathbb{R}_+$
. So, from (2),
![]() $f({{\mathrm{e}}}^x)$
is log-concave in
$f({{\mathrm{e}}}^x)$
is log-concave in
![]() $(\!\log l,\log u)$
if and only if
$(\!\log l,\log u)$
if and only if
for any
![]() $0< s_1 \leq s_2$
and
$0< s_1 \leq s_2$
and
![]() $0< t_1 \leq t_2$
such that these values are inside the interval
$0< t_1 \leq t_2$
such that these values are inside the interval
![]() $(\!\log l,\log u)$
. Now, for any
$(\!\log l,\log u)$
. Now, for any
![]() $\epsilon \geq 1$
such that
$\epsilon \geq 1$
such that
![]() $l\leq x \leq y \leq y \epsilon \leq u$
, consider the following values:
$l\leq x \leq y \leq y \epsilon \leq u$
, consider the following values:
![]() $s_1=x$
,
$s_1=x$
,
![]() $s_2=\epsilon y$
,
$s_2=\epsilon y$
,
![]() $t_1=1$
, and
$t_1=1$
, and
![]() $t_2=\epsilon$
. Thus the desired result follows since
$t_2=\epsilon$
. Thus the desired result follows since
![]() $s_1=x\leq y \leq \epsilon y=s_2 $
and
$s_1=x\leq y \leq \epsilon y=s_2 $
and
![]() $t_1=1\leq \epsilon=t_2$
.
$t_1=1\leq \epsilon=t_2$
.
(Sufficiency) Let us assume now that (3) holds and let
![]() $g(x)=\log(f({{\mathrm{e}}}^x))$
. Since f is Lebesgue-measurable, hence so is g. Letting
$g(x)=\log(f({{\mathrm{e}}}^x))$
. Since f is Lebesgue-measurable, hence so is g. Letting
![]() $x=y$
in inequality (3), we have
$x=y$
in inequality (3), we have
for all
![]() $\epsilon \geq 1$
such that
$\epsilon \geq 1$
such that
![]() $l\leq y\leq y\epsilon \leq u$
. Taking
$l\leq y\leq y\epsilon \leq u$
. Taking
![]() $y={{\mathrm{e}}}^x$
and
$y={{\mathrm{e}}}^x$
and
![]() $\epsilon={{\mathrm{e}}}^c$
, we get
$\epsilon={{\mathrm{e}}}^c$
, we get
for all real numbers x and c such that
![]() $c>0$
and
$c>0$
and
![]() $\log l\leq x-c \leq x+c\leq \log u$
. Let
$\log l\leq x-c \leq x+c\leq \log u$
. Let
![]() $a=x-c$
and
$a=x-c$
and
![]() $b=x+c$
. Then
$b=x+c$
. Then
for all real numbers a and b. So, g is mid-concave (for the definition and properties of mid-concavity, we refer the readers to [Reference Roberts and Varberg22]). As g is mid-concave and Lebesgue-measurable, then it is continuous (see e.g. [Reference Roberts and Varberg22, p. 221]). Now, since mid-concavity with continuity implies concavity, g is concave and thus
![]() $f({{\mathrm{e}}}^x)$
is log-concave.
$f({{\mathrm{e}}}^x)$
is log-concave.
Let
![]() $X_1,\dots,X_n$
be a random sample of size n formed with i.i.d. random variables with a common cumulative distribution function (CDF)
$X_1,\dots,X_n$
be a random sample of size n formed with i.i.d. random variables with a common cumulative distribution function (CDF)
![]() $F(x)=\mathbb{P}(X\le x)$
and survival (or reliability) function (SF)
$F(x)=\mathbb{P}(X\le x)$
and survival (or reliability) function (SF)
![]() $\bar{F}(x)=\mathbb{P}(X>x)$
. We denote the SF of its order statistics
$\bar{F}(x)=\mathbb{P}(X>x)$
. We denote the SF of its order statistics
![]() $X_{1:n}\leq \dots \leq X_{n:n}$
by
$X_{1:n}\leq \dots \leq X_{n:n}$
by
![]() $\bar{F}_{k:n}$
for
$\bar{F}_{k:n}$
for
![]() $k=1,\ldots,n$
. From expression (2.2.15) in [Reference Arnold, Balakrishnan and Nagaraja4], the SF of the kth-order statistic can be written as
$k=1,\ldots,n$
. From expression (2.2.15) in [Reference Arnold, Balakrishnan and Nagaraja4], the SF of the kth-order statistic can be written as
![]() $\bar F_{k:n}(x)= G_{k:n}(\bar F(x))$
, where
$\bar F_{k:n}(x)= G_{k:n}(\bar F(x))$
, where
is the CDF of a beta distribution. To get the proof of our main result, we would also need the following technical lemma.
Lemma 2. If
![]() $G_{k:n}$
is defined as in (4), then
$G_{k:n}$
is defined as in (4), then
![]() $G_{k:n}({{\mathrm{e}}}^x)$
is log-concave in
$G_{k:n}({{\mathrm{e}}}^x)$
is log-concave in
![]() $({-}\infty,0)$
for
$({-}\infty,0)$
for
![]() $k=1,\dots, n$
.
$k=1,\dots, n$
.
Proof. The function
![]() $G_{k:n}({{\mathrm{e}}}^x)$
is log-concave in
$G_{k:n}({{\mathrm{e}}}^x)$
is log-concave in
![]() $({-}\infty,0)$
if and only if
$({-}\infty,0)$
if and only if
![]() $\psi(x)=\log G_{k:n}({{\mathrm{e}}}^x)$
is concave in
$\psi(x)=\log G_{k:n}({{\mathrm{e}}}^x)$
is concave in
![]() $({-}\infty,0)$
. This property holds if
$({-}\infty,0)$
. This property holds if
is decreasing in
![]() $({-}\infty,0)$
, where
$({-}\infty,0)$
, where
and
![]() $\alpha(u)=ug_{k:n}(u)/G_{k:n}(u)$
. A straightforward calculation shows that the function
$\alpha(u)=ug_{k:n}(u)/G_{k:n}(u)$
. A straightforward calculation shows that the function
![]() $\alpha$
is decreasing in (0,1) for
$\alpha$
is decreasing in (0,1) for
![]() $k=1,\dots, n$
.
$k=1,\dots, n$
.
Finally we include here the basic definitions and properties of systems needed for our results. For more properties we refer the reader to [Reference Barlow and Proschan5] and [Reference Navarro20]. A system with n components is a Boolean function
![]() $\phi\,:\, \{0,1\}^n\to\{0,1\}$
, where
$\phi\,:\, \{0,1\}^n\to\{0,1\}$
, where
![]() $x_i=1$
(resp. 0) indicates that the ith component works (does not work) and where the state of the system
$x_i=1$
(resp. 0) indicates that the ith component works (does not work) and where the state of the system
![]() $\phi(x_1,\dots,x_n)$
just depends on the state of these components. A system is semi-coherent if
$\phi(x_1,\dots,x_n)$
just depends on the state of these components. A system is semi-coherent if
![]() $\phi$
is increasing,
$\phi$
is increasing,
![]() $\phi(0,\dots,0)=0$
and
$\phi(0,\dots,0)=0$
and
![]() $\phi(1,\dots,1)=1$
. A system is coherent if
$\phi(1,\dots,1)=1$
. A system is coherent if
![]() $\phi$
is increasing and it is strictly increasing in each variable for at least one point (see [Reference Barlow and Proschan5]).
$\phi$
is increasing and it is strictly increasing in each variable for at least one point (see [Reference Barlow and Proschan5]).
Another well-known property is that the lifetime T of a system is also a function of the lifetimes
![]() $X_1,\dots,X_n$
of its components. Moreover, if these component lifetimes have a common SF function
$X_1,\dots,X_n$
of its components. Moreover, if these component lifetimes have a common SF function
![]() $\bar F(t)=\mathbb{P}(X_i>t)$
, then the system SF
$\bar F(t)=\mathbb{P}(X_i>t)$
, then the system SF
![]() $\bar F_T(t)=\mathbb{P}(T>t)$
can be written as (see e.g. Theorem 2.11 of [Reference Navarro20])
$\bar F_T(t)=\mathbb{P}(T>t)$
can be written as (see e.g. Theorem 2.11 of [Reference Navarro20])
for all t, where
![]() $\bar q\,:\, [0,1]\to[0,1]$
is a distortion function, that is, it is continuous, increasing, and satisfies
$\bar q\,:\, [0,1]\to[0,1]$
is a distortion function, that is, it is continuous, increasing, and satisfies
![]() $\bar q(0)=0$
and
$\bar q(0)=0$
and
![]() $\bar q(1)=1$
. This function
$\bar q(1)=1$
. This function
![]() $\bar q$
does not depend on
$\bar q$
does not depend on
![]() $\bar F$
. In Theorem 4.1 of [Reference Navarro20] it is proved that if
$\bar F$
. In Theorem 4.1 of [Reference Navarro20] it is proved that if
![]() $\bar F$
is absolutely continuous and
$\bar F$
is absolutely continuous and
![]() $\bar q$
is differentiable in (0,1), then the IFR (DFR) class is preserved if and only if the function
$\bar q$
is differentiable in (0,1), then the IFR (DFR) class is preserved if and only if the function
![]() $\alpha(u)=u\bar q^{\prime}(u)/\bar q(u)$
is decreasing (increasing) in (0,1). It can be proved that this alpha function is decreasing for
$\alpha(u)=u\bar q^{\prime}(u)/\bar q(u)$
is decreasing (increasing) in (0,1). It can be proved that this alpha function is decreasing for
![]() $T=X_{k:n}$
and i.i.d. components, that is, the IFR class is preserved under the formation of k-out-of-n in the i.i.d. continuous case. However, the DFR class is not preserved in these systems except in the case of series systems.
$T=X_{k:n}$
and i.i.d. components, that is, the IFR class is preserved under the formation of k-out-of-n in the i.i.d. continuous case. However, the DFR class is not preserved in these systems except in the case of series systems.
3. Preservation of the IFR class in the discrete case
Let us suppose in this section that X is a discrete random variable with ordered support
![]() $S_X=\{x_i\}_{i\in I}$
, with
$S_X=\{x_i\}_{i\in I}$
, with
![]() $x_i<x_{i+1}$
for all
$x_i<x_{i+1}$
for all
![]() $i,i+1\in I$
and probability mass function (PMF)
$i,i+1\in I$
and probability mass function (PMF)
![]() $p(x)=\mathbb{P}(X=x)$
. The failure rate of a discrete distribution is (see [Reference Johnson, Kemp and Kotz13, p. 45])
$p(x)=\mathbb{P}(X=x)$
. The failure rate of a discrete distribution is (see [Reference Johnson, Kemp and Kotz13, p. 45])
Then we say that X is IFR (DFR) if and only if
![]() $h(x_i)$
is increasing (decreasing) in i, which is equivalent to
$h(x_i)$
is increasing (decreasing) in i, which is equivalent to
![]() $\bar{F}(x_{i})/\bar{F}(x_{i-1})$
is decreasing (increasing) in i. This property holds if and only if
$\bar{F}(x_{i})/\bar{F}(x_{i-1})$
is decreasing (increasing) in i. This property holds if and only if
Let us now study the preservation of the IFR/DFR ageing classes in k-out-of-n systems. First we note that it is not difficult to see that the DFR class is not preserved under the formation of k-out-of-n systems in the discrete case by constructing a parallel system with two components having a common geometric distribution which are both DFR and IFR. Both IFR and DFR classes are closed under the formation of series systems with n i.i.d. components because their survival functions are
![]() $(\bar F(x))^n$
for
$(\bar F(x))^n$
for
![]() $n=1,2,\dots$
.
$n=1,2,\dots$
.
Now we focus on the preservation of the IFR property in the discrete case.
Theorem 1. Let X be a discrete random variable with ordered support
![]() $\{x_i\}_{i\in I}$
. Let
$\{x_i\}_{i\in I}$
. Let
![]() $X_1,\dots,X_n$
be independent random variables with the same distribution as X. If X is IFR, then
$X_1,\dots,X_n$
be independent random variables with the same distribution as X. If X is IFR, then
![]() $X_{k:n}$
is IFR for
$X_{k:n}$
is IFR for
![]() $k=1,\dots,n$
.
$k=1,\dots,n$
.
Proof. We first note that X is IFR if and only if
for all
![]() $i-1,i,i+1\in I$
. Analogously,
$i-1,i,i+1\in I$
. Analogously,
![]() $X_{k:n}$
is IFR if and only if
$X_{k:n}$
is IFR if and only if
for all
![]() $i-1,i,i+1\in I$
, where
$i-1,i,i+1\in I$
, where
![]() $G_{k:n}$
is the function defined in (4). Then, from Lemmas 1 and 2, we have that
$G_{k:n}$
is the function defined in (4). Then, from Lemmas 1 and 2, we have that
holds for any
![]() $\epsilon \geq 1$
and any
$\epsilon \geq 1$
and any
![]() $0< x \leq y\leq y \epsilon < 1$
. Hence, from (9) with
$0< x \leq y\leq y \epsilon < 1$
. Hence, from (9) with
![]() $x=y=\bar F(x_i)$
and
$x=y=\bar F(x_i)$
and
![]() $\epsilon= \bar F(x_i)/\bar F(x_{i+1})\geq 1$
, we get
$\epsilon= \bar F(x_i)/\bar F(x_{i+1})\geq 1$
, we get
Finally, by using (7) and the fact that
![]() $G_{k:n}$
is non-negative and increasing, we deduce that (8) holds, which concludes the proof.
$G_{k:n}$
is non-negative and increasing, we deduce that (8) holds, which concludes the proof.
The same technique could be applied to other system structures with i.i.d. components or to the case of dependent i.d. components when the common distribution is a discrete distribution
![]() $\bar F$
with ordered support
$\bar F$
with ordered support
![]() $\{x_i\}_{i\in I}$
by using (6). Thus it can be proved that the IFR class is preserved when the function
$\{x_i\}_{i\in I}$
by using (6). Thus it can be proved that the IFR class is preserved when the function
![]() $\alpha$
defined in the preceding section (by using the distortion function of the system) is decreasing. We include a general result in this sense and an example in the following section.
$\alpha$
defined in the preceding section (by using the distortion function of the system) is decreasing. We include a general result in this sense and an example in the following section.
4. General case
First we give a general definition for the IFR ageing class.
Definition 3. Let X be a random variable with SF
![]() $\bar F$
and left-hand end point of the support
$\bar F$
and left-hand end point of the support
![]() $\ell=\inf\{x\,:\, \bar F(x)<1\}$
. Then we say that X (or
$\ell=\inf\{x\,:\, \bar F(x)<1\}$
. Then we say that X (or
![]() $\bar F$
) is IFR if
$\bar F$
) is IFR if
Note that if
![]() $\bar F(t)>0$
, then the condition in (10) implies that
$\bar F(t)>0$
, then the condition in (10) implies that
![]() $X_s\geq_{\textrm{ST}}X_t$
for all
$X_s\geq_{\textrm{ST}}X_t$
for all
![]() $s\leq t$
, where
$s\leq t$
, where
![]() $\geq_{\textrm{ST}}$
denotes the usual stochastic order (see Chapter 1 of [Reference Shaked and Shanthikumar26]) and where
$\geq_{\textrm{ST}}$
denotes the usual stochastic order (see Chapter 1 of [Reference Shaked and Shanthikumar26]) and where
![]() $X_z=(X-z \mid X>z)$
represents the residual lifetime of X at age z. This is the property used in Theorem 1.A.30 of [Reference Shaked and Shanthikumar26] to characterize the IFR class in the continuous case. Thus the meaning of the IFR property is clear: the younger units are ST-better (more reliable) than the older ones. It also implies that if X has a discrete distribution, then its hazard rate function is increasing in the mass points (see Section 3). If X has an absolutely continuous distribution, then it implies that
$X_z=(X-z \mid X>z)$
represents the residual lifetime of X at age z. This is the property used in Theorem 1.A.30 of [Reference Shaked and Shanthikumar26] to characterize the IFR class in the continuous case. Thus the meaning of the IFR property is clear: the younger units are ST-better (more reliable) than the older ones. It also implies that if X has a discrete distribution, then its hazard rate function is increasing in the mass points (see Section 3). If X has an absolutely continuous distribution, then it implies that
![]() $\bar F$
is log-concave and that there exists a probability density function such that its hazard rate function is increasing. Note that the condition ‘
$\bar F$
is log-concave and that there exists a probability density function such that its hazard rate function is increasing. Note that the condition ‘
![]() $\bar F$
is log-concave’ stated in [Reference Shaked and Shanthikumar26, p. 1] cannot be used in discrete models. However, the general definition given in (10) could be applied to any kind of model (for example, in mixtures of discrete and continuous models). It may also be applied to random variables that can take negative values.
$\bar F$
is log-concave’ stated in [Reference Shaked and Shanthikumar26, p. 1] cannot be used in discrete models. However, the general definition given in (10) could be applied to any kind of model (for example, in mixtures of discrete and continuous models). It may also be applied to random variables that can take negative values.
However, we must note that the DFR ageing class cannot be extended to the general case by reversing the inequality in (10). The reason is that if X has a discrete distribution and
![]() $x_i$
and
$x_i$
and
![]() $x_{i+1}$
are two consecutive mass points, then
$x_{i+1}$
are two consecutive mass points, then
![]() $X_t$
is ST-strictly decreasing in t in the interval
$X_t$
is ST-strictly decreasing in t in the interval
![]() $(x_i,x_{i+1})$
. For example, the geometric distribution does not satisfy this reverse inequality. So the reverse inequality in (10) can only be used in the continuous case.
$(x_i,x_{i+1})$
. For example, the geometric distribution does not satisfy this reverse inequality. So the reverse inequality in (10) can only be used in the continuous case.
Recall from (6) that if T is the lifetime of a semi-coherent system with i.d. components, then the system SF function can be obtained as
![]() $\bar F_T(t)=\bar q(\bar F(t))$
, where
$\bar F_T(t)=\bar q(\bar F(t))$
, where
![]() $\bar q$
is a distortion function. If
$\bar q$
is a distortion function. If
![]() $\bar q$
is strictly increasing and differentiable, then we can state the following general result for the preservation of the IFR class in semi-coherent systems with i.d. components. Note that this result can also be applied to general distorted distributions and for random variables with negative values.
$\bar q$
is strictly increasing and differentiable, then we can state the following general result for the preservation of the IFR class in semi-coherent systems with i.d. components. Note that this result can also be applied to general distorted distributions and for random variables with negative values.
Theorem 2. Let T be the lifetime of a semi-coherent system with i.d. component lifetimes
![]() $X_1,\dots,X_n$
. Let us assume that its distortion function
$X_1,\dots,X_n$
. Let us assume that its distortion function
![]() $\bar q$
in (6) is differentiable in (0,1) and let
$\bar q$
in (6) is differentiable in (0,1) and let
![]() $\alpha(u)=u\bar q^{\prime}(u)/\bar q(u)$
for
$\alpha(u)=u\bar q^{\prime}(u)/\bar q(u)$
for
![]() $u\in (0,1)$
. Then the following conditions are equivalent.
$u\in (0,1)$
. Then the following conditions are equivalent.
-
(i) The IFR ageing property is preserved (that is, if
 $X_1$
is IFR, then T is IFR).
$X_1$
is IFR, then T is IFR). -
(ii) The function
 $\alpha$
is decreasing in (0,1).
$\alpha$
is decreasing in (0,1).
Proof. (i)
![]() $\Rightarrow$
(ii) If
$\Rightarrow$
(ii) If
![]() $X_1$
has a standard exponential model, then it is absolutely continuous and IFR and, from (i), so is T. Hence its hazard rate
$X_1$
has a standard exponential model, then it is absolutely continuous and IFR and, from (i), so is T. Hence its hazard rate
![]() $h_T$
is increasing. As the system SF function is
$h_T$
is increasing. As the system SF function is
![]() $\bar F_T(t)=\bar q(\bar F(t))=\bar q({{\mathrm{e}}}^{-t})$
for all
$\bar F_T(t)=\bar q(\bar F(t))=\bar q({{\mathrm{e}}}^{-t})$
for all
![]() $t\geq 0$
, then its probability density function can be obtained as
$t\geq 0$
, then its probability density function can be obtained as
for all
![]() $t\geq 0$
, where
$t\geq 0$
, where
![]() $f(t)=-\bar F^{\prime}(t)= {{\mathrm{e}}}^{-t}$
is the probability density function of the standard exponential. Hence the system hazard rate function is
$f(t)=-\bar F^{\prime}(t)= {{\mathrm{e}}}^{-t}$
is the probability density function of the standard exponential. Hence the system hazard rate function is
for all
![]() $t\geq 0$
. Then
$t\geq 0$
. Then
![]() $\alpha(u)=h_T({-}\log(u))$
for
$\alpha(u)=h_T({-}\log(u))$
for
![]() $u\in (0,1)$
. Therefore, as
$u\in (0,1)$
. Therefore, as
![]() $h_T$
is increasing in
$h_T$
is increasing in
![]() $(0,\infty)$
,
$(0,\infty)$
,
![]() $\alpha $
is decreasing in (0,1).
$\alpha $
is decreasing in (0,1).
(i)
![]() $\Leftarrow$
(ii) Now we assume that
$\Leftarrow$
(ii) Now we assume that
![]() $\alpha $
is decreasing. Then we consider the function
$\alpha $
is decreasing. Then we consider the function
![]() $\psi(x)=\log\bar q({{\mathrm{e}}}^x)$
for
$\psi(x)=\log\bar q({{\mathrm{e}}}^x)$
for
![]() $x\in({-}\infty,0)$
. Its derivative is
$x\in({-}\infty,0)$
. Its derivative is
Hence
![]() $\psi^{\prime}$
is decreasing in
$\psi^{\prime}$
is decreasing in
![]() $({-}\infty,0)$
. Therefore
$({-}\infty,0)$
. Therefore
![]() $\psi$
is concave and
$\psi$
is concave and
![]() $\bar q({{\mathrm{e}}}^x)$
is log-concave. So we can apply Lemma 2 to the function
$\bar q({{\mathrm{e}}}^x)$
is log-concave. So we can apply Lemma 2 to the function
![]() $\bar q$
in the interval (0,1), that is,
$\bar q$
in the interval (0,1), that is,
for any
![]() $\epsilon \geq 1$
such that
$\epsilon \geq 1$
such that
![]() $0< x \leq y \leq y\epsilon < 1$
. If X is IFR with left-hand end point of the support
$0< x \leq y \leq y\epsilon < 1$
. If X is IFR with left-hand end point of the support
![]() $\ell$
,
$\ell$
,
![]() $\ell\leq s\leq t$
and
$\ell\leq s\leq t$
and
![]() $z\geq 0$
, then
$z\geq 0$
, then
From (6), as
![]() $\bar q$
is strictly increasing, we find that the left-hand end point of the support of T satisfies
$\bar q$
is strictly increasing, we find that the left-hand end point of the support of T satisfies
![]() $\ell_T=\ell$
.
$\ell_T=\ell$
.
Then we have two options. If
![]() $t\geq z+s$
, then
$t\geq z+s$
, then
![]() $\bar F(t)\leq \bar F(z+s)$
. Hence we apply inequality (11) with
$\bar F(t)\leq \bar F(z+s)$
. Hence we apply inequality (11) with
![]() $x=\bar F(t)$
,
$x=\bar F(t)$
,
![]() $y=\bar F(z+s)$
, and
$y=\bar F(z+s)$
, and
![]() $\epsilon=\bar F(s)/\bar F(z+s)\geq 1$
, obtaining
$\epsilon=\bar F(s)/\bar F(z+s)\geq 1$
, obtaining
for s such that
![]() $\bar F(s)>0$
.
$\bar F(s)>0$
.
The other option is when
![]() $t< z+s$
, then
$t< z+s$
, then
![]() $\bar F(t)\geq \bar F(z+s)$
. Hence we apply (11) with
$\bar F(t)\geq \bar F(z+s)$
. Hence we apply (11) with
![]() $y=\bar F(t)$
,
$y=\bar F(t)$
,
![]() $x=\bar F(z+s)$
, and
$x=\bar F(z+s)$
, and
![]() $\epsilon=\bar F(s)/\bar F(t)\geq 1$
, obtaining
$\epsilon=\bar F(s)/\bar F(t)\geq 1$
, obtaining
for s such that
![]() $\bar F(s)>0$
.
$\bar F(s)>0$
.
Finally, by using the fact that X is IFR and
![]() $\bar q$
is increasing, in both options we get
$\bar q$
is increasing, in both options we get
for all
![]() $\ell\leq s\leq t$
and
$\ell\leq s\leq t$
and
![]() $z\geq 0$
. Note that this inequality also holds if
$z\geq 0$
. Note that this inequality also holds if
![]() $\bar F(s)=0$
, since it implies that
$\bar F(s)=0$
, since it implies that
![]() $\bar F(z+s)=0$
for all
$\bar F(z+s)=0$
for all
![]() $z\geq 0$
.
$z\geq 0$
.
Note that the preceding result can be applied to systems with dependent or independent components when they have a common distribution. This distribution can be continuous, discrete, or a mixture. In the preceding section we mentioned that the function
![]() $\alpha$
is always decreasing for k-out-of-n systems with i.i.d. components. Hence, from the preceding theorem, the IFR class is always preserved in k-out-of-n systems with i.i.d. components having a common general reliability function
$\alpha$
is always decreasing for k-out-of-n systems with i.i.d. components. Hence, from the preceding theorem, the IFR class is always preserved in k-out-of-n systems with i.i.d. components having a common general reliability function
![]() $\bar F$
.
$\bar F$
.
However, it should be noted that the IFR property is not preserved in k-out-of-n systems when the components are dependent and i.d. Thus Example 4.3 of [Reference Navarro20] proves that the IFR class is not preserved in
![]() $X_{1:2}$
when the components are dependent with a Clayton copula since
$X_{1:2}$
when the components are dependent with a Clayton copula since
![]() $\alpha$
is strictly increasing.
$\alpha$
is strictly increasing.
Example 4.2 of [Reference Navarro20] proves that the IFR class can be preserved in other systems (i.e. systems without a k-out-of-n structure). It also shows that there exist systems where neither the IFR nor the DFR classes are preserved.
To conclude, the following example shows how to apply Theorem 2 to a general SF
![]() $\bar F$
in a system that does not have a k-out-of-n structure.
$\bar F$
in a system that does not have a k-out-of-n structure.
Example 1. Let us consider the system with lifetime
and let us assume that the component lifetimes are i.i.d. with any IFR distribution. Then the distortion function in (6) is
![]() $\bar q(u)=2u^2-u^3$
and the associated alpha function
$\bar q(u)=2u^2-u^3$
and the associated alpha function
![]() $\alpha (u)=(4-3u)/(2-u)$
is decreasing in (0,1) (see [Reference Navarro20, p. 124]). Then the system is also IFR. This result holds for continuous distributions (Theorem 4.1 of [Reference Navarro20]), discrete distributions with ordered support (preceding section), or in the general case by using Definition 3 and Theorem 2. For example, we can consider the SF
$\alpha (u)=(4-3u)/(2-u)$
is decreasing in (0,1) (see [Reference Navarro20, p. 124]). Then the system is also IFR. This result holds for continuous distributions (Theorem 4.1 of [Reference Navarro20]), discrete distributions with ordered support (preceding section), or in the general case by using Definition 3 and Theorem 2. For example, we can consider the SF
 \begin{equation*}\bar F(t)=\begin{cases}1 & \text{for $ t<0$,}\\p {{\mathrm{e}}}^{-t}& \text{for $ t\geq 0$,}\end{cases}\end{equation*}
\begin{equation*}\bar F(t)=\begin{cases}1 & \text{for $ t<0$,}\\p {{\mathrm{e}}}^{-t}& \text{for $ t\geq 0$,}\end{cases}\end{equation*}
for
![]() $0<p<1$
. It is a mixture of a discrete distribution with mass
$0<p<1$
. It is a mixture of a discrete distribution with mass
![]() $1-p$
at time
$1-p$
at time
![]() $t=0$
and a continuous exponential distribution with mass p in
$t=0$
and a continuous exponential distribution with mass p in
![]() $(0,\infty)$
. A straightforward calculation shows that
$(0,\infty)$
. A straightforward calculation shows that
![]() $\bar F$
is IFR according to Definition 3. Hence so is the system SF
$\bar F$
is IFR according to Definition 3. Hence so is the system SF
![]() $\bar F_T$
.
$\bar F_T$
.
Acknowledgements
We express our sincere thanks to the anonymous reviewers and the Editor-in-Chief for their helpful comments on an earlier version of this manuscript, which led to this improved version. The authors also wish to thank Professor Bara Kim (Korea University) for some fruitful comments.
Funding information
JN thanks the partial support of Ministerio de Ciencia e Innovación of Spain under grant PID2019-103971GB-I00/AEI/10.13039/501100011033.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.