1. Introduction
We consider the problem of estimating a minuscule probability, denoted
![]() $p=\mathbb{P}(A)$
, for some rare event A, using data or Monte Carlo samples. This problem, known as rare-event estimation, is of wide interest to communities such as system reliability [Reference Heidelberger22, Reference Nicola, Nakayama, Heidelberger and Goyal27, Reference Nicola, Shahabuddin and Nakayama28, Reference Tuffin38], queueing systems [Reference Blanchet, Glynn and Lam9, Reference Blanchet and Lam11, Reference Dupuis, Leder and Wang16, Reference Kroese and Nicola25, Reference Ridder30, Reference Sadowsky32, Reference Szechtman and Glynn37], and finance and insurance [Reference Asmussen and Albrecher3, Reference Asmussen4, Reference Collamore14, Reference Glasserman18, Reference Glasserman, Kang and Shahabuddin20, Reference Glasserman and Li21, Reference McNeil, Frey and Embrechts26], where it is crucial to estimate the likelihood of events which, though unlikely, can cause catastrophic impacts.
$p=\mathbb{P}(A)$
, for some rare event A, using data or Monte Carlo samples. This problem, known as rare-event estimation, is of wide interest to communities such as system reliability [Reference Heidelberger22, Reference Nicola, Nakayama, Heidelberger and Goyal27, Reference Nicola, Shahabuddin and Nakayama28, Reference Tuffin38], queueing systems [Reference Blanchet, Glynn and Lam9, Reference Blanchet and Lam11, Reference Dupuis, Leder and Wang16, Reference Kroese and Nicola25, Reference Ridder30, Reference Sadowsky32, Reference Szechtman and Glynn37], and finance and insurance [Reference Asmussen and Albrecher3, Reference Asmussen4, Reference Collamore14, Reference Glasserman18, Reference Glasserman, Kang and Shahabuddin20, Reference Glasserman and Li21, Reference McNeil, Frey and Embrechts26], where it is crucial to estimate the likelihood of events which, though unlikely, can cause catastrophic impacts.
There are multiple prominent lines of work addressing this estimation problem, depending on how information is collected. In settings where real-world data are collected, methods based on extreme value theory [Reference Davison and Smith15, Reference Embrechts, Klüppelberg and Mikosch17, Reference McNeil, Frey and Embrechts26, Reference Smith, de Oliveira and Springer36] are often used to extrapolate distributional tails to assist such estimation. These methods are theoretically justified and widely applicable, but their performance could be affected by intricate hyperparameter choices that affect their accuracy and challenge the reliability in uncertainty quantification [Reference Embrechts, Klüppelberg and Mikosch17]. In settings where A is an event described by a simulable model, Monte Carlo methods can be used, and to speed up computation variance reduction tools such as importance sampling [Reference Juneja, Shahabuddin and Holland24, Reference Sadowsky and Bucklew33, Reference Siegmund35], conditional Monte Carlo [Reference Asmussen and Glynn5, Reference Rubinstein and Kroese31], and multi-level splitting [Reference Au and Beck6, Reference Glasserman, Heidelberger, Shahabuddin and Zajic19, Reference Villén-Altamirano and Villén-Altamirano39] are often harnessed. While variance reduction is greatly beneficial in reducing the number of Monte Carlo samples needed to estimate rare events [Reference Asmussen and Glynn5, Reference Bucklew12, Reference Rubinstein and Kroese31], it is also widely known that they rely heavily on model assumptions [Reference Blanchet and Lam10, Reference Juneja, Shahabuddin and Holland24]. That is, to guarantee the successful performance of these techniques, we typically need to analyze the underlying model dynamics carefully to design the Monte Carlo scheme. However, recent applications, such as autonomous vehicle safety evaluation [Reference Arief2, Reference Huang, Lam, LeBlanc and Zhao23, Reference O’Kelly29, Reference Zhao44, Reference Zhao45] and robustness evaluation of machine learning predictors [Reference Bai, Huang, Lam and Zhao7, Reference Webb, Rainforth, Teh and Kumar42, Reference Weng43], lead to rare-event estimation problems with extremely sophisticated structures that hinder the design of efficiency-guaranteed variance reduction schemes. On the other hand, with the remarkable recent surge in computational infrastructure, in some situations we can afford to run a gigantic number of simulation trials.
Motivated by the limitations of the above techniques and the potential to generate numerous samples, in this paper we focus on a more basic setting than some of the above literature, but in a sense fundamental. More precisely, we focus on the situation where all we have to estimate p is a set of independent and identically distributed (i.i.d.) Bernoulli observations I(A). A natural point estimate of p is the sample proportion
![]() $\hat p$
, i.e. given a set of Bernoulli data
$\hat p$
, i.e. given a set of Bernoulli data
![]() $I_1,\ldots,I_n$
of size n, we output
$I_1,\ldots,I_n$
of size n, we output
![]() $\hat p=(1/n)\sum_{i=1}^nI_i$
. We are interested in understanding the statistical error in using
$\hat p=(1/n)\sum_{i=1}^nI_i$
. We are interested in understanding the statistical error in using
![]() $\hat p$
in the situation where p could be very small, importantly with no lower bound on how small it could be. Unlike the estimates given by efficiency-guaranteed variance reduction techniques, as we will explain, it is not entirely straightforward whether using simple sample proportion can give meaningful guarantees to estimating rare-event probabilities, in relation to the sample size n and the (unknown) magnitude of p. Motivated by this, our main goal in this paper is to study the construction, coverage validity, and tightness of confidence intervals (CIs) for rare-event probabilities using only the simple sample proportion estimator. The main messages from our findings are as follows: The normality and Wilson intervals are not always valid, in the sense that their actual coverage probabilities can be less than the nominal confidence level, but they are shown to be close to our two newly developed valid intervals in terms of half-width. On the other hand, the exact interval is conservative, as its coverage probability is strictly larger than the nominal confidence level and hence it is not as tight as the aforementioned two intervals, but it safely guarantees the attainment of the nominal confidence level. Our new intervals are even more conservative than the exact interval and hence not recommended in practice, but they provide useful insights in understanding the tightness of the normality and Wilson intervals.
$\hat p$
in the situation where p could be very small, importantly with no lower bound on how small it could be. Unlike the estimates given by efficiency-guaranteed variance reduction techniques, as we will explain, it is not entirely straightforward whether using simple sample proportion can give meaningful guarantees to estimating rare-event probabilities, in relation to the sample size n and the (unknown) magnitude of p. Motivated by this, our main goal in this paper is to study the construction, coverage validity, and tightness of confidence intervals (CIs) for rare-event probabilities using only the simple sample proportion estimator. The main messages from our findings are as follows: The normality and Wilson intervals are not always valid, in the sense that their actual coverage probabilities can be less than the nominal confidence level, but they are shown to be close to our two newly developed valid intervals in terms of half-width. On the other hand, the exact interval is conservative, as its coverage probability is strictly larger than the nominal confidence level and hence it is not as tight as the aforementioned two intervals, but it safely guarantees the attainment of the nominal confidence level. Our new intervals are even more conservative than the exact interval and hence not recommended in practice, but they provide useful insights in understanding the tightness of the normality and Wilson intervals.
This paper is organized as follows. Section 2 describes the problem setting and the motivating challenges. Section 3 gives an overview of the existing and new CIs, and Section 4 summarizes our main results. Then, in Sections 5 and 6, we present the details of the derivation and analyses of these intervals. After that, Section 7 reports some numerical results to visualize our comparisons. Section 8 concludes the paper with our findings and recommendations. All missing proofs can be found in the appendix.
2. Problem setting and motivation
Suppose we would like to estimate a target probability p by using information from the Bernoulli data, or equivalently
![]() $\hat p$
. In particular, we would like to construct a CI for p that has justifiable statistical guarantees. In answering this, we would also quantify the error between the point estimate
$\hat p$
. In particular, we would like to construct a CI for p that has justifiable statistical guarantees. In answering this, we would also quantify the error between the point estimate
![]() $\hat p$
and p.
$\hat p$
and p.
First of all, we clarify what a good CI is supposed to be. To this end, we mainly consider the validity of the coverage and tightness. Throughout this paper, we say that
![]() $[\hat p_\mathrm{l}(\alpha),\hat p_\mathrm{u}(\alpha)]$
is a valid
$[\hat p_\mathrm{l}(\alpha),\hat p_\mathrm{u}(\alpha)]$
is a valid
![]() $(1-\alpha)$
-level CI if
$(1-\alpha)$
-level CI if
![]() $\mathbb{P}(\hat p_\mathrm{l}(\alpha)\leq p\leq \hat p_\mathrm{u}(\alpha))\geq 1-\alpha$
. This notion of validity can be defined similarly for one-sided confidence bounds. On the other hand, a good CI should not be too wide; for example, in the extreme case, the trivial CI [0, 1] is valid, but it does not provide any useful information. In this paper, we quantify tightness by the ‘half-width’, i.e.
$\mathbb{P}(\hat p_\mathrm{l}(\alpha)\leq p\leq \hat p_\mathrm{u}(\alpha))\geq 1-\alpha$
. This notion of validity can be defined similarly for one-sided confidence bounds. On the other hand, a good CI should not be too wide; for example, in the extreme case, the trivial CI [0, 1] is valid, but it does not provide any useful information. In this paper, we quantify tightness by the ‘half-width’, i.e.
![]() $\hat p_\mathrm{u}(\alpha)-\hat p$
or
$\hat p_\mathrm{u}(\alpha)-\hat p$
or
![]() $\hat p-\hat p_\mathrm{l}(\alpha)$
(some intervals we consider are symmetric so there is no difference between the ‘upper’ and ‘lower’ half-widths, but some intervals are not, in which case the context would make the meaning of half-width clear). Importantly, considering that p is tiny in the rare-event settings, the CI is meaningful only if the half-width is small relative to p and
$\hat p-\hat p_\mathrm{l}(\alpha)$
(some intervals we consider are symmetric so there is no difference between the ‘upper’ and ‘lower’ half-widths, but some intervals are not, in which case the context would make the meaning of half-width clear). Importantly, considering that p is tiny in the rare-event settings, the CI is meaningful only if the half-width is small relative to p and
![]() $\hat p$
.
$\hat p$
.
To understand the challenges, we first examine the use of a standard ‘textbook’ CI, and we focus on the upper confidence bound for now since the lower confidence bound can be argued analogously. More specifically, we use the following as the
![]() $(1-\alpha)$
-level upper confidence bound:
$(1-\alpha)$
-level upper confidence bound:
where
![]() $z_{1-\alpha}$
is the
$z_{1-\alpha}$
is the
![]() $(1-\alpha)$
-quantile of a standard normal variable. The typical way to justify (1) is a normal approximation using the central limit theorem (CLT), which entails that
$(1-\alpha)$
-quantile of a standard normal variable. The typical way to justify (1) is a normal approximation using the central limit theorem (CLT), which entails that
where we denote by
![]() $\bar\Phi$
(and
$\bar\Phi$
(and
![]() $\Phi$
) the tail (and cumulative) distribution function of the standard normal.
$\Phi$
) the tail (and cumulative) distribution function of the standard normal.
To delve a little further, note that the approximation error in the previous equation is controlled by the Berry–Esseen (BE) theorem. To simplify the discussion, suppose we are in a more idealized (but unrealistic) case where we know the precise value of the variance of the Bernoulli trial, i.e.
![]() $\sigma^2=p(1-p)$
, so that we use
$\sigma^2=p(1-p)$
, so that we use
![]() $\hat p+z_{1-\alpha}\sigma/\sqrt n$
. Then the BE theorem stipulates that
$\hat p+z_{1-\alpha}\sigma/\sqrt n$
. Then the BE theorem stipulates that
where
![]() $\rho=E|I_i-p|^3=p(1-p)(1-2p+2p^2)$
, and C is a universal constant (
$\rho=E|I_i-p|^3=p(1-p)(1-2p+2p^2)$
, and C is a universal constant (
![]() $\approx0.4748$
). Thus, the error in (2) is bounded by
$\approx0.4748$
). Thus, the error in (2) is bounded by
The issue is that when p is tiny, np can also be tiny unless n is sufficiently big, but a priori we would not know what n is ‘sufficient’. If we have used the confidence bound given by (1) where the variance
![]() $\sigma^2$
is unknown and estimated by
$\sigma^2$
is unknown and estimated by
![]() $\hat p(1-\hat p)$
, a similar BE bound would ultimately conclude the same issue as revealed by (3) [Reference Shao and Wang34]. A straightforward idea is to use the number of successes to infer whether n is sufficiently large. Suppose we have, say, 30 ‘success’ outcomes among n trials; then we may think that
$\hat p(1-\hat p)$
, a similar BE bound would ultimately conclude the same issue as revealed by (3) [Reference Shao and Wang34]. A straightforward idea is to use the number of successes to infer whether n is sufficiently large. Suppose we have, say, 30 ‘success’ outcomes among n trials; then we may think that
![]() $np\approx30$
, so that from the bound in (3) the error of
$np\approx30$
, so that from the bound in (3) the error of
![]() $\hat p^\mathrm{CLT}$
appears controlled. As another, more extreme, case, suppose we only have only one success; then we may be led to believe that
$\hat p^\mathrm{CLT}$
appears controlled. As another, more extreme, case, suppose we only have only one success; then we may be led to believe that
![]() $np\approx1$
, so that
$np\approx1$
, so that
![]() $\hat p^\mathrm{CLT}$
is well defined but its coverage is likely way off from
$\hat p^\mathrm{CLT}$
is well defined but its coverage is likely way off from
![]() $1-\alpha$
. However, we note that the guess that
$1-\alpha$
. However, we note that the guess that
![]() $np\approx30$
or
$np\approx30$
or
![]() $np\approx1$
is itself based on some central limit or concentration argument, which apparently leads to circular reasoning. This challenge motivates us to investigate more on the validity and tightness of different CIs in order to make a suitable choice.
$np\approx1$
is itself based on some central limit or concentration argument, which apparently leads to circular reasoning. This challenge motivates us to investigate more on the validity and tightness of different CIs in order to make a suitable choice.
It is well known that a quick and implementable approach to construct a CI that is always valid regardless of n, p, or
![]() $\hat p$
is to utilize the fact that
$\hat p$
is to utilize the fact that
![]() $n\hat p$
follows a binomial distribution and extract a finite-sample confidence region using this exact distribution. This is often called the Clopper–Pearson CI or the exact method [Reference Clopper and Pearson13]. Though this is computationally easy, we are interested in simpler mathematical forms that allow us to analytically study the relative half-width as well. In this regard, Wilson’s interval [Reference Agresti and Coull1] has been studied and shown to give superior empirical performance, even in the case that p is tiny, but we are not aware of any rigorous proof on its validity. In this paper, we propose two different ways of constructing CIs for p that are simultaneously valid and analytically tractable, one using Chernoff’s inequality, and the other one using the BE bound. Compared to the exact CI, these two CIs have explicit forms that allow us to investigate their half-widths, and thereby understand how far the CLT or Wilson CIs are from valid CIs.
$n\hat p$
follows a binomial distribution and extract a finite-sample confidence region using this exact distribution. This is often called the Clopper–Pearson CI or the exact method [Reference Clopper and Pearson13]. Though this is computationally easy, we are interested in simpler mathematical forms that allow us to analytically study the relative half-width as well. In this regard, Wilson’s interval [Reference Agresti and Coull1] has been studied and shown to give superior empirical performance, even in the case that p is tiny, but we are not aware of any rigorous proof on its validity. In this paper, we propose two different ways of constructing CIs for p that are simultaneously valid and analytically tractable, one using Chernoff’s inequality, and the other one using the BE bound. Compared to the exact CI, these two CIs have explicit forms that allow us to investigate their half-widths, and thereby understand how far the CLT or Wilson CIs are from valid CIs.
Finally, in simulation analysis and some real-data situations, it is natural to keep sampling until we observe enough successes (e.g. when the number of successes is 30) in the experiments. We also adapt the existing or newly developed CIs to this setup and investigate their performance.
3. Overview of confidence intervals
Here we briefly introduce the formulas of the CIs that we study in this paper. We consider two settings. The first one is called the ‘standard’ setting, where the sample size n is fixed. The other setting is when we fix the number of successes
![]() $\hat{s}=n\hat p$
, which we call the ‘targeted stopping’ setting. Under each setting, we discuss three existing CIs: the CLT CI, Wilson CI, and exact CI. We also introduce how to construct our new Chernoff CI and the BE CI via inverting Chernoff’s inequality and the BE theorem.
$\hat{s}=n\hat p$
, which we call the ‘targeted stopping’ setting. Under each setting, we discuss three existing CIs: the CLT CI, Wilson CI, and exact CI. We also introduce how to construct our new Chernoff CI and the BE CI via inverting Chernoff’s inequality and the BE theorem.
3.1. Confidence intervals under the standard setting
Under the standard setting, to construct valid CIs our starting point is the following set:
where
![]() $F(x)=\mathbb{P}(\hat p\leq x)$
and
$F(x)=\mathbb{P}(\hat p\leq x)$
and
![]() $F_-(x)=\mathbb{P}(\hat p<x)$
. Note that F and
$F_-(x)=\mathbb{P}(\hat p<x)$
. Note that F and
![]() $F_-$
depend on p. If F were continuous, we know that
$F_-$
depend on p. If F were continuous, we know that
![]() $\mathbb{P}(F(\hat p)\geq\alpha/2,\,F_-(\hat p)\leq 1-\alpha/2)=1-\alpha$
since in this case
$\mathbb{P}(F(\hat p)\geq\alpha/2,\,F_-(\hat p)\leq 1-\alpha/2)=1-\alpha$
since in this case
![]() $F(\hat p)=F_-(\hat p)\stackrel{\mathrm{d}}{=}\mathrm{Uniform}[0,1]$
. Now we argue that
$F(\hat p)=F_-(\hat p)\stackrel{\mathrm{d}}{=}\mathrm{Uniform}[0,1]$
. Now we argue that
![]() $\mathbb{P}(F(\hat p)\geq\alpha/2,\,F_-(\hat p)\leq 1-\alpha/2)>1-\alpha$
in this discrete case. Indeed, for any
$\mathbb{P}(F(\hat p)\geq\alpha/2,\,F_-(\hat p)\leq 1-\alpha/2)>1-\alpha$
in this discrete case. Indeed, for any
![]() $\alpha\in(0,1)$
, there exist
$\alpha\in(0,1)$
, there exist
![]() $0\leq k,l\leq n$
such that
$0\leq k,l\leq n$
such that
![]() $F((k-1)/n)<\alpha/2\leq F(k/n)$
and
$F((k-1)/n)<\alpha/2\leq F(k/n)$
and
![]() $F_-(l/n)\leq 1-\alpha/2<F_-((l+1)/n)$
. Then
$F_-(l/n)\leq 1-\alpha/2<F_-((l+1)/n)$
. Then
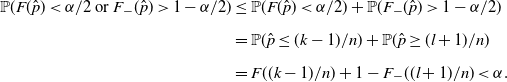 \begin{align*} \mathbb{P}(F(\hat p)<\alpha/2\text{ or }F_-(\hat p)>1-\alpha/2) & \leq \mathbb{P}(F(\hat p)<\alpha/2)+\mathbb{P}(F_-(\hat p)>1-\alpha/2) \\[5pt] & = \mathbb{P}(\hat p\leq (k-1)/n)+\mathbb{P}(\hat p\geq (l+1)/n) \\[5pt] & = F((k-1)/n)+1-F_-((l+1)/n)<\alpha.\end{align*}
\begin{align*} \mathbb{P}(F(\hat p)<\alpha/2\text{ or }F_-(\hat p)>1-\alpha/2) & \leq \mathbb{P}(F(\hat p)<\alpha/2)+\mathbb{P}(F_-(\hat p)>1-\alpha/2) \\[5pt] & = \mathbb{P}(\hat p\leq (k-1)/n)+\mathbb{P}(\hat p\geq (l+1)/n) \\[5pt] & = F((k-1)/n)+1-F_-((l+1)/n)<\alpha.\end{align*}
Therefore, the set (4) is a valid
![]() $(1-\alpha)$
-level confidence region. From this derivation, we find that, due to the discreteness, the probability that this confidence region covers the true value p is strictly larger than the nominal confidence level
$(1-\alpha)$
-level confidence region. From this derivation, we find that, due to the discreteness, the probability that this confidence region covers the true value p is strictly larger than the nominal confidence level
![]() $1-\alpha$
, and hence this confidence region is inevitably conservative.
$1-\alpha$
, and hence this confidence region is inevitably conservative.
The CLT and Wilson CIs can be obtained from (4) by estimating
![]() $F(\hat p)$
and
$F(\hat p)$
and
![]() $F_-(\hat p)$
via normal approximation. As a result, these two CIs are no longer guaranteed to be valid. More specifically, using the fact that
$F_-(\hat p)$
via normal approximation. As a result, these two CIs are no longer guaranteed to be valid. More specifically, using the fact that
![]() $({\hat p-p})/{\sqrt{\hat p(1-\hat p)/n}}\approx N(0,1)$
, we substitute
$({\hat p-p})/{\sqrt{\hat p(1-\hat p)/n}}\approx N(0,1)$
, we substitute
into (4) to obtain the CLT CI.
Definition 1. (CLT CI under the standard setting.) Suppose that we estimate the probability
![]() $p=\mathbb{P}(A)$
for the event A, and
$p=\mathbb{P}(A)$
for the event A, and
![]() $\hat p$
is the sample proportion of hitting A in n i.i.d. trials. Under this setting, the CLT CI is defined by:
$\hat p$
is the sample proportion of hitting A in n i.i.d. trials. Under this setting, the CLT CI is defined by:
Similarly, since
![]() $({\hat p-p})/{\sqrt{p(1-p)/n}}\approx N(0,1)$
and substituting
$({\hat p-p})/{\sqrt{p(1-p)/n}}\approx N(0,1)$
and substituting
we get the Wilson CI.
Definition 2. (Wilson CI under the standard setting.) Suppose that we estimate the probability
![]() $p=\mathbb{P}(A)$
for the event A, and
$p=\mathbb{P}(A)$
for the event A, and
![]() $\hat p$
is the sample proportion of hitting A in n i.i.d. trials. Under this setting, the Wilson CI is defined by:
$\hat p$
is the sample proportion of hitting A in n i.i.d. trials. Under this setting, the Wilson CI is defined by:
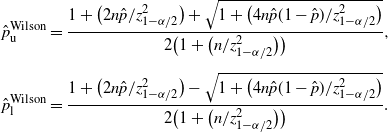 \begin{align*} \hat{p}_\mathrm{u}^\mathrm{Wilson} & = \frac{1+\big({2n\hat{p}}/{z_{1-\alpha/2}^2}\big)+\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{1-\alpha/2}^2}\big)}} {2\big(1+\big({n}/{z_{1-\alpha/2}^2}\big)\big)}, \\[5pt] \hat{p}_\mathrm{l}^\mathrm{Wilson} & = \frac{1+\big({2n\hat{p}}/{z_{1-\alpha/2}^2}\big)-\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{1-\alpha/2}^2}\big)}} {2\big(1+\big({n}/{z_{1-\alpha/2}^2}\big)\big)}. \end{align*}
\begin{align*} \hat{p}_\mathrm{u}^\mathrm{Wilson} & = \frac{1+\big({2n\hat{p}}/{z_{1-\alpha/2}^2}\big)+\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{1-\alpha/2}^2}\big)}} {2\big(1+\big({n}/{z_{1-\alpha/2}^2}\big)\big)}, \\[5pt] \hat{p}_\mathrm{l}^\mathrm{Wilson} & = \frac{1+\big({2n\hat{p}}/{z_{1-\alpha/2}^2}\big)-\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{1-\alpha/2}^2}\big)}} {2\big(1+\big({n}/{z_{1-\alpha/2}^2}\big)\big)}. \end{align*}
Instead of using normal approximation, the exact CI directly solves the valid confidence region (4). In fact, we know that
![]() $\hat{s}=n\hat p\sim \mathrm{Binomial}(n, p)$
, so the functions
$\hat{s}=n\hat p\sim \mathrm{Binomial}(n, p)$
, so the functions
![]() $F(\!\cdot\!)$
and
$F(\!\cdot\!)$
and
![]() $F_-(\!\cdot\!)$
have exact expressions. More specifically, we have the following definition.
$F_-(\!\cdot\!)$
have exact expressions. More specifically, we have the following definition.
Definition 3. (Exact CI under the standard setting.) Suppose that we estimate the probability
![]() $p=\mathbb{P}(A)$
for the event A, and
$p=\mathbb{P}(A)$
for the event A, and
![]() $\hat p$
is the sample proportion of hitting A in n i.i.d. trials. Under this setting, the exact CI is defined by
$\hat p$
is the sample proportion of hitting A in n i.i.d. trials. Under this setting, the exact CI is defined by
![]() $[\hat{p}^\mathrm{Exact}_\mathrm{l},\hat{p}^\mathrm{Exact}_\mathrm{u}]$
, where
$[\hat{p}^\mathrm{Exact}_\mathrm{l},\hat{p}^\mathrm{Exact}_\mathrm{u}]$
, where
![]() $\hat{p}^\mathrm{Exact}_\mathrm{u}$
and
$\hat{p}^\mathrm{Exact}_\mathrm{u}$
and
![]() $\hat{p}^\mathrm{Exact}_\mathrm{l}$
are the respective solutions to
$\hat{p}^\mathrm{Exact}_\mathrm{l}$
are the respective solutions to
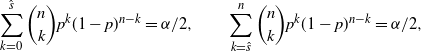 \begin{equation*} \sum_{k=0}^{\hat{s}}\binom{n}{k}p^k(1-p)^{n-k} = \alpha/2, \qquad \sum_{k=\hat{s}}^n\binom{n}{k}p^k(1-p)^{n-k} = \alpha/2, \end{equation*}
\begin{equation*} \sum_{k=0}^{\hat{s}}\binom{n}{k}p^k(1-p)^{n-k} = \alpha/2, \qquad \sum_{k=\hat{s}}^n\binom{n}{k}p^k(1-p)^{n-k} = \alpha/2, \end{equation*}
except that
![]() $\hat{p}^\mathrm{Exact}_\mathrm{u}=1$
if
$\hat{p}^\mathrm{Exact}_\mathrm{u}=1$
if
![]() $\hat{s}=n$
and
$\hat{s}=n$
and
![]() $\hat{p}^\mathrm{Exact}_\mathrm{l}=0$
if
$\hat{p}^\mathrm{Exact}_\mathrm{l}=0$
if
![]() $\hat{s}=0$
.
$\hat{s}=0$
.
When
![]() $0<\hat{s}<n$
, the bounds could be expressed explicitly via quantiles of the F distribution or Beta distribution, and hence are easy to compute numerically [Reference Agresti and Coull1]. However, it is hard to analyze the scale of this CI, which motivates us to further relax the confidence region (4) to get other valid CIs that are more conservative but easier to analyze.
$0<\hat{s}<n$
, the bounds could be expressed explicitly via quantiles of the F distribution or Beta distribution, and hence are easy to compute numerically [Reference Agresti and Coull1]. However, it is hard to analyze the scale of this CI, which motivates us to further relax the confidence region (4) to get other valid CIs that are more conservative but easier to analyze.
In order to relax (4), we respectively consider using two methods: Chernoff’s inequality and the BE theorem. We will only present the formulas for them here and leave the details of their development to Section 5.1.
Definition 4. (Chernoff CI under the standard setting.) Suppose that we estimate the probability
![]() $p=\mathbb{P}(A)$
for the event A, and
$p=\mathbb{P}(A)$
for the event A, and
![]() $\hat p$
is the sample proportion of hitting A in n i.i.d. trials. Under this setting, the Chernoff CI is defined by:
$\hat p$
is the sample proportion of hitting A in n i.i.d. trials. Under this setting, the Chernoff CI is defined by:
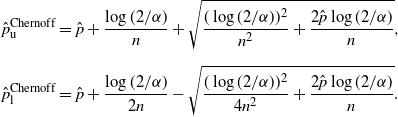 \begin{align*} \hat{p}^\mathrm{Chernoff}_\mathrm{u} & = \hat{p}+\frac{\log(2/\alpha)}{n}+\sqrt{\frac{(\log(2/\alpha))^2}{n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}},\\[5pt] \hat{p}^\mathrm{Chernoff}_\mathrm{l} & = \hat{p}+\frac{\log(2/\alpha)}{2n}-\sqrt{\frac{(\log(2/\alpha))^2}{4n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}}. \end{align*}
\begin{align*} \hat{p}^\mathrm{Chernoff}_\mathrm{u} & = \hat{p}+\frac{\log(2/\alpha)}{n}+\sqrt{\frac{(\log(2/\alpha))^2}{n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}},\\[5pt] \hat{p}^\mathrm{Chernoff}_\mathrm{l} & = \hat{p}+\frac{\log(2/\alpha)}{2n}-\sqrt{\frac{(\log(2/\alpha))^2}{4n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}}. \end{align*}
Definition 5. (BE CI under the standard setting.) Suppose that we estimate the probability
![]() $p=\mathbb{P}(A)$
for the event A, and
$p=\mathbb{P}(A)$
for the event A, and
![]() $\hat p$
is the sample proportion of hitting A in n i.i.d. trials. In addition, we assume that
$\hat p$
is the sample proportion of hitting A in n i.i.d. trials. In addition, we assume that
![]() $p<\frac12$
. Under this setting, the BE CI is solved from
$p<\frac12$
. Under this setting, the BE CI is solved from
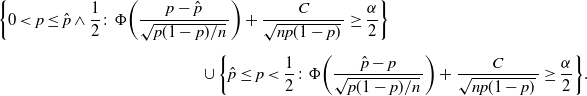 \begin{multline*} \bigg\{0<p\leq \hat p\wedge\frac12\colon \Phi\bigg(\frac{p-\hat{p}}{\sqrt{p(1-p)/n}\,}\bigg)+\frac{C}{\sqrt{np(1-p)}\,}\geq\frac{\alpha}{2}\bigg\} \\[5pt] \cup \bigg\{\hat p\leq p<\frac12\colon \Phi\bigg(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}\,}\bigg)+\frac{C}{\sqrt{np(1-p)}\,}\geq\frac{\alpha}{2}\bigg\}. \end{multline*}
\begin{multline*} \bigg\{0<p\leq \hat p\wedge\frac12\colon \Phi\bigg(\frac{p-\hat{p}}{\sqrt{p(1-p)/n}\,}\bigg)+\frac{C}{\sqrt{np(1-p)}\,}\geq\frac{\alpha}{2}\bigg\} \\[5pt] \cup \bigg\{\hat p\leq p<\frac12\colon \Phi\bigg(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}\,}\bigg)+\frac{C}{\sqrt{np(1-p)}\,}\geq\frac{\alpha}{2}\bigg\}. \end{multline*}
3.2. Confidence intervals under targeted stopping
Now we consider experiments where we keep sampling until we get
![]() $n_0$
successes. Under this setting, the sample size N is a random variable. More specifically,
$n_0$
successes. Under this setting, the sample size N is a random variable. More specifically,
![]() $N=N_1+\cdots+N_{n_0}$
, where
$N=N_1+\cdots+N_{n_0}$
, where
![]() $N_1,\ldots,N_{n_0}$
are i.i.d. Geometric(p) random variables, or, equivalently,
$N_1,\ldots,N_{n_0}$
are i.i.d. Geometric(p) random variables, or, equivalently,
![]() $N-n_0$
follows a negative binomial distribution
$N-n_0$
follows a negative binomial distribution
![]() $\mathrm{NB}(n_0,p)$
. Note that
$\mathrm{NB}(n_0,p)$
. Note that
![]() $N\ge n_0$
. We define
$N\ge n_0$
. We define
![]() $F_N(x)=\mathbb{P}(N\leq x)$
and
$F_N(x)=\mathbb{P}(N\leq x)$
and
![]() $F_{N-}(x)=\mathbb{P}(N<x)$
. Similar to Section 3.1, we argue that the following set is a valid
$F_{N-}(x)=\mathbb{P}(N<x)$
. Similar to Section 3.1, we argue that the following set is a valid
![]() $(1-\alpha)$
-level confidence region for p:
$(1-\alpha)$
-level confidence region for p:
Indeed, for any
![]() $\alpha\in(0,1)$
, there exist
$\alpha\in(0,1)$
, there exist
![]() $1\leq k,l<\infty$
such that
$1\leq k,l<\infty$
such that
![]() $F_N(k-1)<\alpha/2\leq F_N(k)$
and
$F_N(k-1)<\alpha/2\leq F_N(k)$
and
![]() $F_{N-}(l)\leq 1-\alpha/2<F_{N-}(l+1)$
. Then
$F_{N-}(l)\leq 1-\alpha/2<F_{N-}(l+1)$
. Then
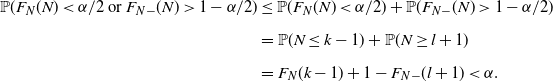 \begin{align*} \mathbb{P}(F_N(N)<\alpha/2\text{ or }F_{N-}(N)>1-\alpha/2) & \leq \mathbb{P}(F_N(N)<\alpha/2)+\mathbb{P}(F_{N-}(N)>1-\alpha/2) \\[5pt] & = \mathbb{P}(N\leq k-1)+\mathbb{P}(N\geq l+1) \\[5pt] & = F_N(k-1)+1-F_{N-}(l+1)<\alpha.\end{align*}
\begin{align*} \mathbb{P}(F_N(N)<\alpha/2\text{ or }F_{N-}(N)>1-\alpha/2) & \leq \mathbb{P}(F_N(N)<\alpha/2)+\mathbb{P}(F_{N-}(N)>1-\alpha/2) \\[5pt] & = \mathbb{P}(N\leq k-1)+\mathbb{P}(N\geq l+1) \\[5pt] & = F_N(k-1)+1-F_{N-}(l+1)<\alpha.\end{align*}
By definition, the set (5) is a valid
![]() $(1-\alpha)$
-level confidence region.
$(1-\alpha)$
-level confidence region.
We could still use the CLT and Wilson CIs with
![]() $\hat p=n_0/N$
. More specifically, we have the following definitions.
$\hat p=n_0/N$
. More specifically, we have the following definitions.
Definition 6. (CLT CI under targeted stopping.) Suppose that we estimate the probability
![]() $p=\mathbb{P}(A)$
for the event A. We keep sampling until we get
$p=\mathbb{P}(A)$
for the event A. We keep sampling until we get
![]() $n_0$
successes and the sample size is denoted by N. Under this setting, the CLT CI is defined by:
$n_0$
successes and the sample size is denoted by N. Under this setting, the CLT CI is defined by:
Definition 7. (Wilson CI under targeted stopping.) Suppose that we estimate the probability
![]() $p=\mathbb{P}(A)$
for the event A. We keep sampling until we get
$p=\mathbb{P}(A)$
for the event A. We keep sampling until we get
![]() $n_0$
successes and the sample size is denoted by N. Under this setting, the Wilson CI is defined by:
$n_0$
successes and the sample size is denoted by N. Under this setting, the Wilson CI is defined by:
 \begin{align*} \hat{p}_{\mathrm{u},n_0}^\mathrm{Wilson} & = \frac{1+\big({2n_0}/{z_{1-\alpha/2}^2}\big)+\sqrt{1+\big({4n_0(N-n_0)}/{z_{1-\alpha/2}^2N}\big)}} {2\big(1+\big({N}/{z_{1-\alpha/2}^2}\big)\big)}, \\[5pt] \hat{p}_{\mathrm{l},n_0}^\mathrm{Wilson} & = \frac{1+\big({2n_0}/{z_{1-\alpha/2}^2}\big)-\sqrt{1+\big({4n_0(N-n_0)}/{z_{1-\alpha/2}^2N}\big)}} {2\big(1+\big({N}/{z_{1-\alpha/2}^2}\big)\big)}. \end{align*}
\begin{align*} \hat{p}_{\mathrm{u},n_0}^\mathrm{Wilson} & = \frac{1+\big({2n_0}/{z_{1-\alpha/2}^2}\big)+\sqrt{1+\big({4n_0(N-n_0)}/{z_{1-\alpha/2}^2N}\big)}} {2\big(1+\big({N}/{z_{1-\alpha/2}^2}\big)\big)}, \\[5pt] \hat{p}_{\mathrm{l},n_0}^\mathrm{Wilson} & = \frac{1+\big({2n_0}/{z_{1-\alpha/2}^2}\big)-\sqrt{1+\big({4n_0(N-n_0)}/{z_{1-\alpha/2}^2N}\big)}} {2\big(1+\big({N}/{z_{1-\alpha/2}^2}\big)\big)}. \end{align*}
Similar to the standard setting, we can directly solve (5) using the exact distribution of N.
Definition 8. (Exact CI under targeted stopping.) Suppose that we estimate the probability
![]() $p=\mathbb{P}(A)$
for the event A. We keep sampling until we get
$p=\mathbb{P}(A)$
for the event A. We keep sampling until we get
![]() $n_0$
successes and the sample size is denoted by N. Under this setting, the exact CI is defined by
$n_0$
successes and the sample size is denoted by N. Under this setting, the exact CI is defined by
![]() $\big[\hat{p}_{\mathrm{l},n_0}^\mathrm{Exact},\hat{p}_{\mathrm{u},n_0}^\mathrm{Exact}\big]$
where
$\big[\hat{p}_{\mathrm{l},n_0}^\mathrm{Exact},\hat{p}_{\mathrm{u},n_0}^\mathrm{Exact}\big]$
where
![]() $\hat{p}_{\mathrm{u},n_0}^\mathrm{Exact}$
and
$\hat{p}_{\mathrm{u},n_0}^\mathrm{Exact}$
and
![]() $\hat{p}_{\mathrm{l},n_0}^\mathrm{Exact}$
are the respective solutions to
$\hat{p}_{\mathrm{l},n_0}^\mathrm{Exact}$
are the respective solutions to
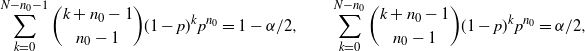 \begin{equation*} \sum_{k=0}^{N-n_0-1}\binom{k+n_0-1}{n_0-1}(1-p)^kp^{n_0} = 1-\alpha/2, \qquad \sum_{k=0}^{N-n_0}\binom{k+n_0-1}{n_0-1}(1-p)^kp^{n_0} = \alpha/2, \end{equation*}
\begin{equation*} \sum_{k=0}^{N-n_0-1}\binom{k+n_0-1}{n_0-1}(1-p)^kp^{n_0} = 1-\alpha/2, \qquad \sum_{k=0}^{N-n_0}\binom{k+n_0-1}{n_0-1}(1-p)^kp^{n_0} = \alpha/2, \end{equation*}
except that
![]() $\hat{p}_{\mathrm{u},n_0}^\mathrm{Exact}=1$
if
$\hat{p}_{\mathrm{u},n_0}^\mathrm{Exact}=1$
if
![]() $N=n_0$
.
$N=n_0$
.
While the interval is easy to compute numerically, it is not easy to analyze. Similar to the standard setting, we relax the confidence region (5) to construct valid CIs via respectively inverting Chernoff’s inequality and the BE theorem. We leave the details of developing these two new CIs to Section 6.1 and only present the formulas here.
Definition 9. (Chernoff CI under targeted stopping.) Suppose that we estimate the probability
![]() $p=\mathbb{P}(A)$
for the event A. We keep sampling until we get
$p=\mathbb{P}(A)$
for the event A. We keep sampling until we get
![]() $n_0$
successes and the sample size is denoted by N. Under this setting, the Chernoff CI is solved from
$n_0$
successes and the sample size is denoted by N. Under this setting, the Chernoff CI is solved from
Definition 10. (BE CI under targeted stopping.) Suppose that we estimate the probability
![]() $p=\mathbb{P}(A)$
for the event A. We keep sampling until we get
$p=\mathbb{P}(A)$
for the event A. We keep sampling until we get
![]() $n_0$
successes and the sample size is denoted by N. In addition, we assume that
$n_0$
successes and the sample size is denoted by N. In addition, we assume that
![]() $p<\frac12$
. Under this setting, the BE CI is defined by:
$p<\frac12$
. Under this setting, the BE CI is defined by:
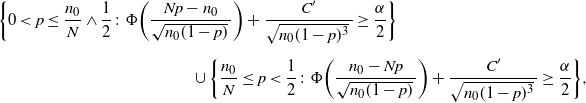 \begin{multline*} \bigg\{0< p\leq\frac{n_0}{N}\wedge\frac12\colon\Phi\bigg(\frac{Np-n_0}{\sqrt{n_0(1-p)}\,}\bigg) + \frac{C'}{\sqrt{n_0(1-p)^3}\,} \geq \frac{\alpha}{2}\bigg\} \\[5pt] \cup \bigg\{\frac{n_0}{N}\leq p<\frac{1}{2}\colon\Phi\bigg(\frac{n_0-Np}{\sqrt{n_0(1-p)}\,}\bigg) + \frac{C'}{\sqrt{n_0(1-p)^3}\,} \geq \frac{\alpha}{2}\bigg\}, \end{multline*}
\begin{multline*} \bigg\{0< p\leq\frac{n_0}{N}\wedge\frac12\colon\Phi\bigg(\frac{Np-n_0}{\sqrt{n_0(1-p)}\,}\bigg) + \frac{C'}{\sqrt{n_0(1-p)^3}\,} \geq \frac{\alpha}{2}\bigg\} \\[5pt] \cup \bigg\{\frac{n_0}{N}\leq p<\frac{1}{2}\colon\Phi\bigg(\frac{n_0-Np}{\sqrt{n_0(1-p)}\,}\bigg) + \frac{C'}{\sqrt{n_0(1-p)^3}\,} \geq \frac{\alpha}{2}\bigg\}, \end{multline*}
where
![]() $C'=16C$
is a universal constant.
$C'=16C$
is a universal constant.
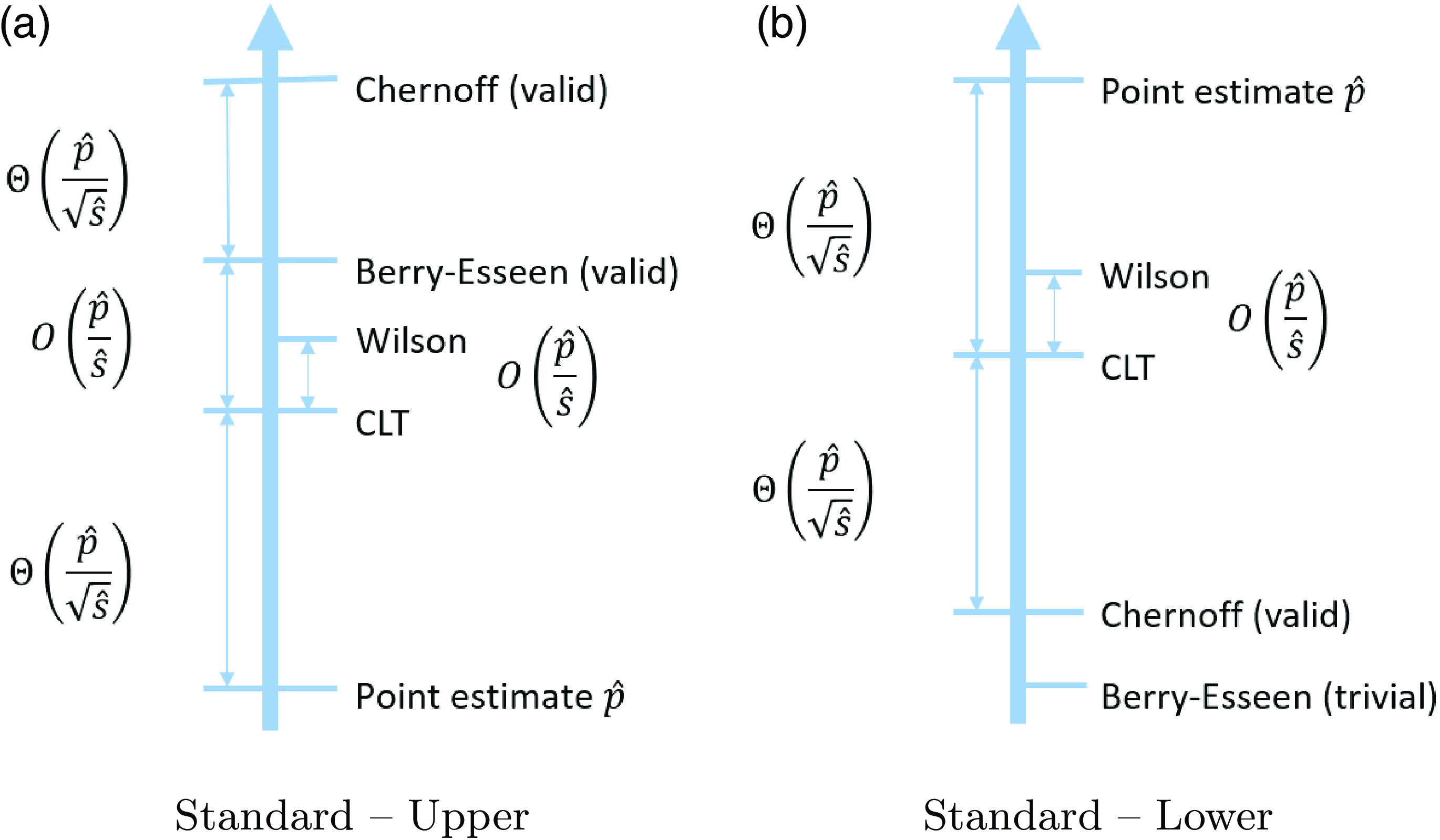
Figure 1. Comparisons of the positions of confidence upper and lower bounds under the standard setting. Here, ‘valid’ means that the CI has valid coverage in the sense that the actual coverage probability always reaches the nominal confidence level.
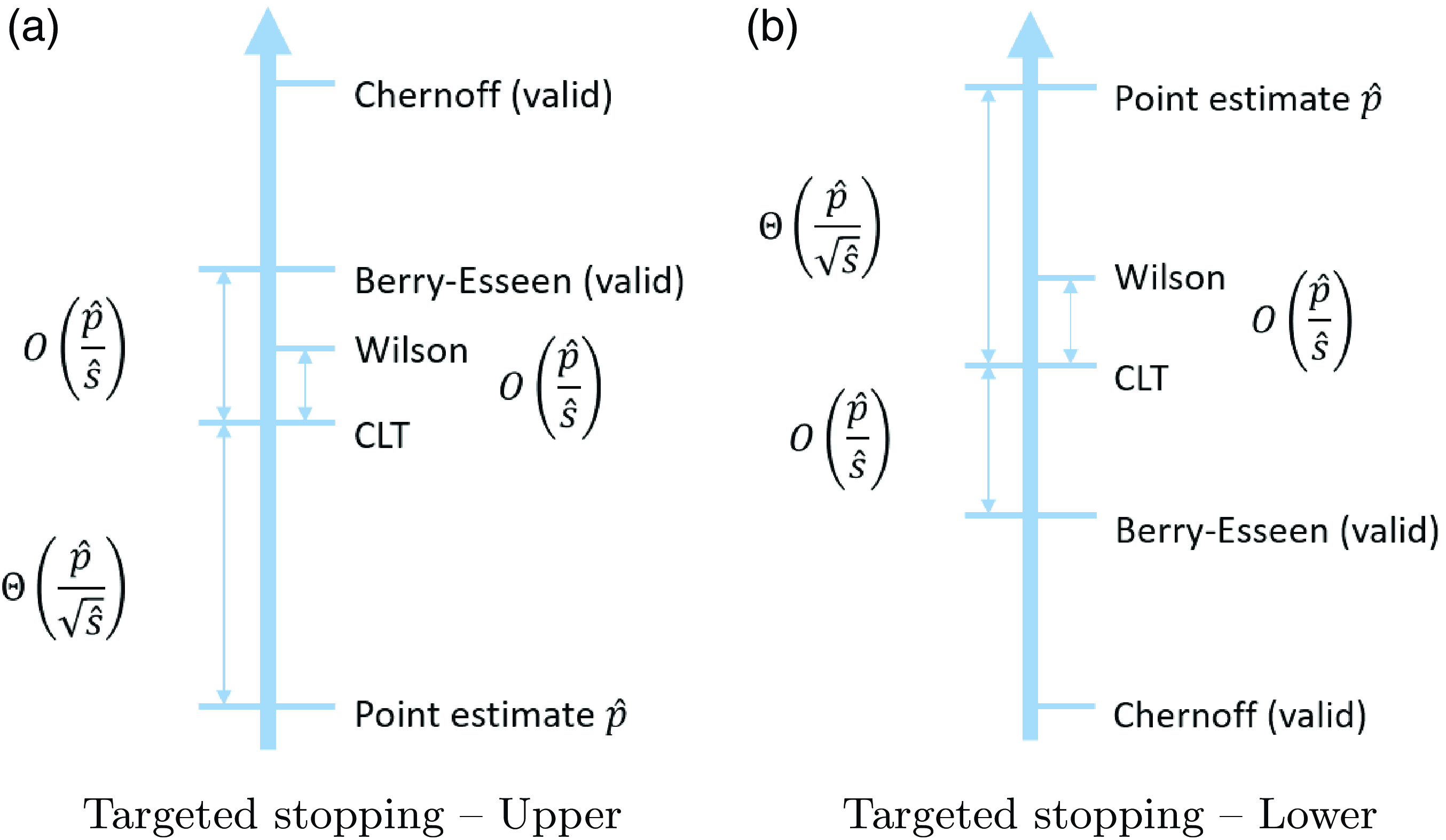
Figure 2. Comparisons of the positions of confidence upper and lower bounds under the targeted stopping setting. Here, ‘valid’ means that the CI has valid coverage in the sense that the actual coverage probability always reaches the nominal confidence level.
4. Summary of the main results
As explained in Section 2, when we compare different CIs we mainly consider the validity in terms of coverage probability, and tightness in terms of half-width. In terms of validity, the existing CLT and Wilson CIs do not possess guarantees, while the exact CI, and our new Chernoff CI and BE CI, are valid by construction. The half-widths of the CIs, which will be analyzed in detail in Sections 5.2 and 6.2, are summarized in Figures 1 and 2. In particular, these figures illustrate comparisons of these CIs in terms of upper and lower bound (the exact CI is not included since it is hard to analyze its magnitude). For instance, from (1), we clearly see that the half-width of the CLT CI scales at the same order as
![]() $\sqrt{\hat p/n}=\hat p/\sqrt{\hat{s}}$
, where
$\sqrt{\hat p/n}=\hat p/\sqrt{\hat{s}}$
, where
![]() $\hat{s}=n\hat p$
is the number of positive outcomes. By expressing
$\hat{s}=n\hat p$
is the number of positive outcomes. By expressing
![]() $\sqrt{\hat p/n}$
as
$\sqrt{\hat p/n}$
as
![]() $\hat p/\sqrt{\hat{s}}$
here, it is easier to see how the half-width scales relative to
$\hat p/\sqrt{\hat{s}}$
here, it is easier to see how the half-width scales relative to
![]() $\hat p$
. That is, the relative half-width is of order
$\hat p$
. That is, the relative half-width is of order
![]() $1/\sqrt{\hat{s}}$
. Note that in these figures, under the standard setting, for
$1/\sqrt{\hat{s}}$
. Note that in these figures, under the standard setting, for
![]() $f(n,\hat p),g(n,\hat p)\geq 0$
, we write
$f(n,\hat p),g(n,\hat p)\geq 0$
, we write
![]() $f=O(g)$
if there exist
$f=O(g)$
if there exist
![]() $N_0,p_0,M>0$
, which do not depend on p or
$N_0,p_0,M>0$
, which do not depend on p or
![]() $\hat p$
, such that, for any
$\hat p$
, such that, for any
![]() $n\hat p>N_0$
and
$n\hat p>N_0$
and
![]() $\hat p<p_0$
,
$\hat p<p_0$
,
![]() $f\leq Mg$
; we write
$f\leq Mg$
; we write
![]() $f=\Theta(g)$
if there exist
$f=\Theta(g)$
if there exist
![]() $N_0,p_0,M_1,M_2>0$
, which do not depend on p or
$N_0,p_0,M_1,M_2>0$
, which do not depend on p or
![]() $\hat p$
, such that, for any
$\hat p$
, such that, for any
![]() $n\hat p>N_0$
and
$n\hat p>N_0$
and
![]() $\hat p<p_0$
,
$\hat p<p_0$
,
![]() $M_1g\leq f\leq M_2g$
. Under the targeted stopping setting,
$M_1g\leq f\leq M_2g$
. Under the targeted stopping setting,
![]() $O(\!\cdot\!)$
and
$O(\!\cdot\!)$
and
![]() $\Theta(\!\cdot\!)$
are defined similarly by replacing
$\Theta(\!\cdot\!)$
are defined similarly by replacing
![]() $n\hat p$
with
$n\hat p$
with
![]() $n_0$
. The notations
$n_0$
. The notations
![]() $O(\!\cdot\!)$
and
$O(\!\cdot\!)$
and
![]() $\Theta(\!\cdot\!)$
will be used throughout the rest of this paper.
$\Theta(\!\cdot\!)$
will be used throughout the rest of this paper.
More concretely, Tables 1 and 2 summarize the formulas, scales, pros, and cons of each CI under the standard and targeted stopping settings respectively. The key findings can be summarized as follows:
-
The CLT CI is the ‘textbook’ normality interval and thus very intuitive, but its coverage probability can be far below the nominal level. However, in terms of the half-width, except for the lower bound in the standard setting, the difference between the CLT bound and the valid BE bound is of order
 $\hat p/\hat{s}$
, so the relative difference with respect to
$\hat p/\hat{s}$
, so the relative difference with respect to
 $\hat p$
is of order
$\hat p$
is of order
 $1/\hat{s}$
, which is of higher order in
$1/\hat{s}$
, which is of higher order in
 $\hat{s}$
than its relative half-width. This can be viewed as a relatively small price of validity paid to make the CLT bound correct. For the lower bound in the standard setting, the BE bound is trivial, so we cannot come to a similar conclusion. However, in this case the difference between the CLT bound and the valid Chernoff bound is of order
$\hat{s}$
than its relative half-width. This can be viewed as a relatively small price of validity paid to make the CLT bound correct. For the lower bound in the standard setting, the BE bound is trivial, so we cannot come to a similar conclusion. However, in this case the difference between the CLT bound and the valid Chernoff bound is of order
 $\hat p/\sqrt{\hat{s}}$
, the same order as the half-width, which shows that the CLT bound has roughly the correct magnitude.
$\hat p/\sqrt{\hat{s}}$
, the same order as the half-width, which shows that the CLT bound has roughly the correct magnitude. -
In practice, the Wilson CI has satisfactory performance, in the sense that it is relatively tight while the coverage probability is usually close to the nominal confidence level. The difference between the Wilson and CLT bounds is of order
 $\hat p/\hat{s}$
, which is of higher order in
$\hat p/\hat{s}$
, which is of higher order in
 $\hat{s}$
than the half-width. As a result, the conclusions for the CLT CI regarding the difference from the valid BE and Chernoff CIs still hold for the Wilson CI.
$\hat{s}$
than the half-width. As a result, the conclusions for the CLT CI regarding the difference from the valid BE and Chernoff CIs still hold for the Wilson CI. -
The exact CI is, as aforementioned, inevitably conservative, in the sense that its coverage probability is strictly higher than the nominal level. However, it is the tightest among the valid CIs, so it is recommended when we want the nominal confidence level to be guaranteed. The Chernoff and BE CIs are valid but extremely conservative. They are not recommended for use in practice, but their analytical forms help us gain useful insights on the CLT and Wilson CIs. That is, now we learn that the CLT and Wilson CIs, although not always valid, are relatively close to these two valid CIs as mentioned in the first bullet point.
5. Developments under the standard setting
We present in detail the construction of the new Chernoff and BE CIs that endows their validity (Section 5.1). Then we analyze the half-widths of all the CIs discussed here (Section 5.2).
5.1. Derivation of new confidence intervals
5.1.1. Chernoff’s CI
Now we present our first approach to construct a valid CI for p by relaxing (4). By Chernoff’s inequality, we have
Table 1. Summary of the CIs in the standard setting (
![]() $I_1,\dots,I_n \stackrel{\mathrm{i.i.d.}}{\sim}\mathrm{Bernoulli}(p)$
,
$I_1,\dots,I_n \stackrel{\mathrm{i.i.d.}}{\sim}\mathrm{Bernoulli}(p)$
,
![]() $\hat{p}=({1}/{n})\sum_{i=1}^n I_i$
,
$\hat{p}=({1}/{n})\sum_{i=1}^n I_i$
,
![]() $\hat{s}=n\hat p$
).
$\hat{s}=n\hat p$
).

Table 2. Summary of the CIs in the targeted stopping setting (
![]() $N_1,\dots,N_{n_0}\stackrel{\mathrm{i.i.d.}}{\sim}\mathrm{Geometric}(p)$
,
$N_1,\dots,N_{n_0}\stackrel{\mathrm{i.i.d.}}{\sim}\mathrm{Geometric}(p)$
,
![]() $N=\sum_{i=1}^{n_0}N_i$
,
$N=\sum_{i=1}^{n_0}N_i$
,
![]() $\hat p=n_0/N$
).
$\hat p=n_0/N$
).

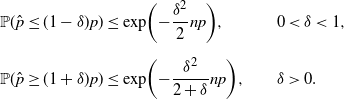 \begin{alignat*}{2} \mathbb{P}(\hat{p}\leq(1-\delta)p) & \leq \exp\!\bigg({-}\frac{\delta^2}{2}np\bigg), & & 0<\delta<1, \\[5pt] \mathbb{P}(\hat{p}\geq(1+\delta)p) & \leq \exp\!\bigg({-}\frac{\delta^2}{2+\delta}np\bigg), \qquad & & \delta>0.\end{alignat*}
\begin{alignat*}{2} \mathbb{P}(\hat{p}\leq(1-\delta)p) & \leq \exp\!\bigg({-}\frac{\delta^2}{2}np\bigg), & & 0<\delta<1, \\[5pt] \mathbb{P}(\hat{p}\geq(1+\delta)p) & \leq \exp\!\bigg({-}\frac{\delta^2}{2+\delta}np\bigg), \qquad & & \delta>0.\end{alignat*}
Replacing
![]() $(1-\delta)p$
or
$(1-\delta)p$
or
![]() $(1+\delta)p$
by x, we have
$(1+\delta)p$
by x, we have
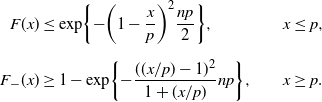 \begin{alignat*}{2} F(x) & \leq \exp\!\bigg\{{-}\bigg(1-\frac{x}{p}\bigg)^2\frac{np}{2}\bigg\}, & & x\leq p, \\[5pt] F_-(x) & \geq 1-\exp\!\bigg\{{-}\frac{(({x}/{p})-1)^2}{1+({x}/{p})}np\bigg\}, \qquad & & x\geq p.\end{alignat*}
\begin{alignat*}{2} F(x) & \leq \exp\!\bigg\{{-}\bigg(1-\frac{x}{p}\bigg)^2\frac{np}{2}\bigg\}, & & x\leq p, \\[5pt] F_-(x) & \geq 1-\exp\!\bigg\{{-}\frac{(({x}/{p})-1)^2}{1+({x}/{p})}np\bigg\}, \qquad & & x\geq p.\end{alignat*}
Hence,
![]() $F(\hat{p})\geq\alpha/2$
,
$F(\hat{p})\geq\alpha/2$
,
![]() $F_-(\hat{p})\leq1-\alpha/2$
implies that
$F_-(\hat{p})\leq1-\alpha/2$
implies that
Therefore,
is a confidence region for
![]() $\hat p$
with confidence level at least
$\hat p$
with confidence level at least
![]() $1-\alpha$
. Simplifying the above expression, we have
$1-\alpha$
. Simplifying the above expression, we have
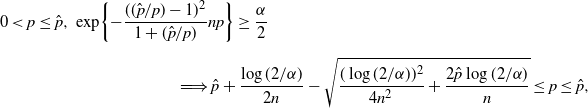 \begin{multline*} 0<p\leq\hat p,\ \exp\!\bigg\{{-}\frac{(({\hat p}/{p})-1)^2}{1+({\hat p}/{p})}np\bigg\} \geq \frac{\alpha}{2} \\[5pt] \Longrightarrow \hat{p}+\frac{\log(2/\alpha)}{2n}-\sqrt{\frac{(\log(2/\alpha))^2}{4n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}}\leq p\leq \hat p,\end{multline*}
\begin{multline*} 0<p\leq\hat p,\ \exp\!\bigg\{{-}\frac{(({\hat p}/{p})-1)^2}{1+({\hat p}/{p})}np\bigg\} \geq \frac{\alpha}{2} \\[5pt] \Longrightarrow \hat{p}+\frac{\log(2/\alpha)}{2n}-\sqrt{\frac{(\log(2/\alpha))^2}{4n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}}\leq p\leq \hat p,\end{multline*}
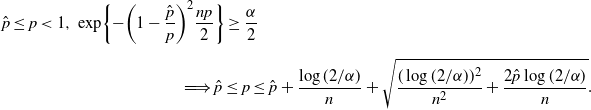 \begin{multline*} \hat{p}\leq p<1,\ \exp\!\bigg\{{-}\bigg(1-\frac{\hat p}{p}\bigg)^2\frac{np}{2}\bigg\} \geq \frac{\alpha}{2} \\[5pt] \Longrightarrow \hat p\leq p\leq\hat{p}+\frac{\log(2/\alpha)}{n} + \sqrt{\frac{(\log(2/\alpha))^2}{n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}}.\end{multline*}
\begin{multline*} \hat{p}\leq p<1,\ \exp\!\bigg\{{-}\bigg(1-\frac{\hat p}{p}\bigg)^2\frac{np}{2}\bigg\} \geq \frac{\alpha}{2} \\[5pt] \Longrightarrow \hat p\leq p\leq\hat{p}+\frac{\log(2/\alpha)}{n} + \sqrt{\frac{(\log(2/\alpha))^2}{n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}}.\end{multline*}
Hence, by taking the union, we get a valid
![]() $(1-\alpha)$
-level CI for p, for any finite sample n. This id summarized in the following theorem.
$(1-\alpha)$
-level CI for p, for any finite sample n. This id summarized in the following theorem.
Theorem 1. (Validity of Chernoff CI under the standard setting.) The interval given by
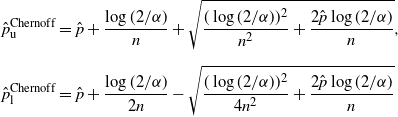 \begin{align*} \hat{p}^\mathrm{Chernoff}_\mathrm{u} & = \hat{p} + \frac{\log(2/\alpha)}{n} + \sqrt{\frac{(\log(2/\alpha))^2}{n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}}, \\[5pt] \hat{p}^\mathrm{Chernoff}_\mathrm{l} & = \hat{p} + \frac{\log(2/\alpha)}{2n} - \sqrt{\frac{(\log(2/\alpha))^2}{4n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}} \end{align*}
\begin{align*} \hat{p}^\mathrm{Chernoff}_\mathrm{u} & = \hat{p} + \frac{\log(2/\alpha)}{n} + \sqrt{\frac{(\log(2/\alpha))^2}{n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}}, \\[5pt] \hat{p}^\mathrm{Chernoff}_\mathrm{l} & = \hat{p} + \frac{\log(2/\alpha)}{2n} - \sqrt{\frac{(\log(2/\alpha))^2}{4n^2}+\frac{2\hat{p}\log(2/\alpha)}{n}} \end{align*}
is a valid
![]() $(1-\alpha)$
-level CI for p, for any finite sample n. That is, for any n,
$(1-\alpha)$
-level CI for p, for any finite sample n. That is, for any n,
5.1.2. BE CI
We develop another CI for p by inverting the BE theorem. Here, we assume that p is known to satisfy
![]() $p<\frac12$
a priori (which is reasonable if we consider rare events). In this paper, we use the standard version of the BE theorem, and a potential future investigation is to consider a BE bound for the studentized statistic [Reference Wang and Hall40, Reference Wang and Jing41].
$p<\frac12$
a priori (which is reasonable if we consider rare events). In this paper, we use the standard version of the BE theorem, and a potential future investigation is to consider a BE bound for the studentized statistic [Reference Wang and Hall40, Reference Wang and Jing41].
By the BE theorem,
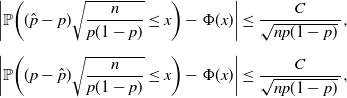 \begin{align*} \bigg|\mathbb{P}\bigg((\hat{p}-p)\sqrt{\frac{n}{p(1-p)}}\le x\bigg) - \Phi(x)\bigg| & \le \frac{C}{\sqrt{np(1-p)}\,}, \\[5pt] \bigg|\mathbb{P}\bigg((p-\hat p)\sqrt{\frac{n}{p(1-p)}}\le x\bigg) - \Phi(x)\bigg| & \le \frac{C}{\sqrt{np(1-p)}\,},\end{align*}
\begin{align*} \bigg|\mathbb{P}\bigg((\hat{p}-p)\sqrt{\frac{n}{p(1-p)}}\le x\bigg) - \Phi(x)\bigg| & \le \frac{C}{\sqrt{np(1-p)}\,}, \\[5pt] \bigg|\mathbb{P}\bigg((p-\hat p)\sqrt{\frac{n}{p(1-p)}}\le x\bigg) - \Phi(x)\bigg| & \le \frac{C}{\sqrt{np(1-p)}\,},\end{align*}
where C is a universal constant. We replace x by
![]() $({\hat{p}-p})/{\sqrt{p(1-p)/n}}$
in the first inequality and
$({\hat{p}-p})/{\sqrt{p(1-p)/n}}$
in the first inequality and
![]() $({p-\hat{p}})/{\sqrt{p(1-p)/n}}$
in the second one. Then,
$({p-\hat{p}})/{\sqrt{p(1-p)/n}}$
in the second one. Then,
 \begin{align*} \bigg|F(\hat{p})-\Phi\bigg(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}\,}\bigg)\bigg| & \leq \frac{C}{\sqrt{np(1-p)}\,}, \\[5pt] \bigg|1-F_-(\hat{p})-\Phi\bigg(\frac{p-\hat{p}}{\sqrt{p(1-p)/n}\,}\bigg)\bigg| & \leq \frac{C}{\sqrt{np(1-p)}\,}.\end{align*}
\begin{align*} \bigg|F(\hat{p})-\Phi\bigg(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}\,}\bigg)\bigg| & \leq \frac{C}{\sqrt{np(1-p)}\,}, \\[5pt] \bigg|1-F_-(\hat{p})-\Phi\bigg(\frac{p-\hat{p}}{\sqrt{p(1-p)/n}\,}\bigg)\bigg| & \leq \frac{C}{\sqrt{np(1-p)}\,}.\end{align*}
Hence,
![]() $F(\hat{p})\geq\alpha/2$
,
$F(\hat{p})\geq\alpha/2$
,
![]() $F_-(\hat{p})\leq1-\alpha/2$
implies that either
$F_-(\hat{p})\leq1-\alpha/2$
implies that either
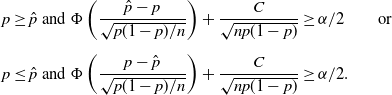 \begin{align*} p\geq\hat{p}\text{ and }\Phi\left(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}}\right)+\frac{C}{\sqrt{np(1-p)}} & \geq \alpha/2 \qquad \text{or } \\[5pt] p\leq\hat{p}\text{ and }\Phi\left(\frac{p-\hat{p}}{\sqrt{p(1-p)/n}}\right)+\frac{C}{\sqrt{np(1-p)}} & \geq \alpha/2.\end{align*}
\begin{align*} p\geq\hat{p}\text{ and }\Phi\left(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}}\right)+\frac{C}{\sqrt{np(1-p)}} & \geq \alpha/2 \qquad \text{or } \\[5pt] p\leq\hat{p}\text{ and }\Phi\left(\frac{p-\hat{p}}{\sqrt{p(1-p)/n}}\right)+\frac{C}{\sqrt{np(1-p)}} & \geq \alpha/2.\end{align*}
Thus,
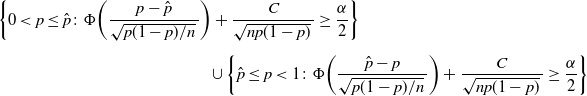 \begin{multline*} \bigg\{0<p\leq\hat p \colon \Phi\bigg(\frac{p-\hat{p}}{\sqrt{p(1-p)/n}\,}\bigg) + \frac{C}{\sqrt{np(1-p)}\,} \geq \frac{\alpha}{2}\bigg\} \\[5pt] \cup \bigg\{\hat p\leq p<1 \colon \Phi\bigg(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}\,}\bigg) + \frac{C}{\sqrt{np(1-p)}\,} \geq \frac{\alpha}{2}\bigg\}\end{multline*}
\begin{multline*} \bigg\{0<p\leq\hat p \colon \Phi\bigg(\frac{p-\hat{p}}{\sqrt{p(1-p)/n}\,}\bigg) + \frac{C}{\sqrt{np(1-p)}\,} \geq \frac{\alpha}{2}\bigg\} \\[5pt] \cup \bigg\{\hat p\leq p<1 \colon \Phi\bigg(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}\,}\bigg) + \frac{C}{\sqrt{np(1-p)}\,} \geq \frac{\alpha}{2}\bigg\}\end{multline*}
is a valid
![]() $(1-\alpha)$
-level confidence region for p. Since we have assumed that
$(1-\alpha)$
-level confidence region for p. Since we have assumed that
![]() $p<\frac12$
, the above confidence region can be shrunk further. To summarize, we have the following theorem.
$p<\frac12$
, the above confidence region can be shrunk further. To summarize, we have the following theorem.
Theorem 2. (Validity of BE CI under the standard setting.) Assume that
![]() $p<\frac12$
. Then the set
$p<\frac12$
. Then the set
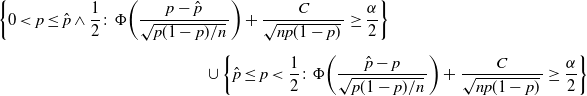 \begin{multline} \bigg\{0<p\leq\hat p\wedge\frac12\colon\Phi\bigg(\frac{p-\hat{p}}{\sqrt{p(1-p)/n}\,}\bigg) + \frac{C}{\sqrt{np(1-p)}\,} \geq \frac{\alpha}{2}\bigg\} \\[5pt] \cup \bigg\{\hat p\leq p<\frac12\colon\Phi\bigg(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}\,}\bigg) + \frac{C}{\sqrt{np(1-p)}\,} \geq \frac{\alpha}{2}\bigg\} \end{multline}
\begin{multline} \bigg\{0<p\leq\hat p\wedge\frac12\colon\Phi\bigg(\frac{p-\hat{p}}{\sqrt{p(1-p)/n}\,}\bigg) + \frac{C}{\sqrt{np(1-p)}\,} \geq \frac{\alpha}{2}\bigg\} \\[5pt] \cup \bigg\{\hat p\leq p<\frac12\colon\Phi\bigg(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}\,}\bigg) + \frac{C}{\sqrt{np(1-p)}\,} \geq \frac{\alpha}{2}\bigg\} \end{multline}
is a valid
![]() $(1-\alpha)$
-level confidence region for p, for any finite sample n.
$(1-\alpha)$
-level confidence region for p, for any finite sample n.
5.2. Analyses of half-widths
5.2.1. CLT CI
Clearly,
![]() $\hat{p}_\mathrm{u}^\mathrm{CLT}-\hat p=\Theta(\sqrt{\hat p/n})=\Theta(\hat p/\sqrt{\hat{s}})$
and
$\hat{p}_\mathrm{u}^\mathrm{CLT}-\hat p=\Theta(\sqrt{\hat p/n})=\Theta(\hat p/\sqrt{\hat{s}})$
and
![]() $\hat{p}-\hat{p}_\mathrm{l}^\mathrm{CLT}=\Theta(\hat p/\sqrt{\hat{s}})$
. As explained in Section 2, we express the half-width as
$\hat{p}-\hat{p}_\mathrm{l}^\mathrm{CLT}=\Theta(\hat p/\sqrt{\hat{s}})$
. As explained in Section 2, we express the half-width as
![]() $\Theta(\hat p/\sqrt{\hat{s}})$
instead of
$\Theta(\hat p/\sqrt{\hat{s}})$
instead of
![]() $\Theta(\sqrt{\hat p/n})$
in order to understand the magnitude of the relative half-width with respect to
$\Theta(\sqrt{\hat p/n})$
in order to understand the magnitude of the relative half-width with respect to
![]() $\hat p$
more clearly.
$\hat p$
more clearly.
5.2.2. Wilson CI
We derive the following theorem through some algebraic manipulations.
Theorem 3. (Half-width of the Wilson CI under the standard setting.)
Note that
![]() $1/n=\hat p/\hat{s}$
, so the difference between the Wilson and CLT CIs is of order
$1/n=\hat p/\hat{s}$
, so the difference between the Wilson and CLT CIs is of order
![]() $O(\hat p/\hat{s})$
, which is of higher order than
$O(\hat p/\hat{s})$
, which is of higher order than
![]() $\hat p/\sqrt{\hat{s}}$
in
$\hat p/\sqrt{\hat{s}}$
in
![]() $\hat{s}$
. In fact, as long as
$\hat{s}$
. In fact, as long as
![]() $\hat{s}\geq 1$
, i.e. we have at least one positive observation, then
$\hat{s}\geq 1$
, i.e. we have at least one positive observation, then
![]() $\hat p/\sqrt{\hat{s}}=\sqrt{\hat{p}/n}=\sqrt{\hat{s}}/n\geq 1/n$
. Since the half-width of the CLT CI is of order
$\hat p/\sqrt{\hat{s}}=\sqrt{\hat{p}/n}=\sqrt{\hat{s}}/n\geq 1/n$
. Since the half-width of the CLT CI is of order
![]() $\hat p/\sqrt{\hat{s}}$
, we get that the half-width of the Wilson CI is close to the CLT CI.
$\hat p/\sqrt{\hat{s}}$
, we get that the half-width of the Wilson CI is close to the CLT CI.
5.2.3. Chernoff CI
When
![]() $\hat p=0$
, the Chernoff CI reduces to
$\hat p=0$
, the Chernoff CI reduces to
![]() $[0, 2\log(1/\alpha)/n]$
(and in fact we can construct even tighter bounds by using the binomial distribution of
$[0, 2\log(1/\alpha)/n]$
(and in fact we can construct even tighter bounds by using the binomial distribution of
![]() $n\hat p$
directly in this case). On the other hand, when
$n\hat p$
directly in this case). On the other hand, when
![]() $\hat p>0$
, we can re-express using
$\hat p>0$
, we can re-express using
![]() $\hat{s}=n\hat p$
to get
$\hat{s}=n\hat p$
to get
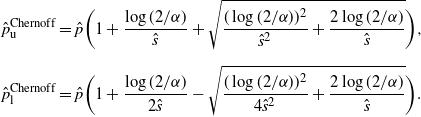 \begin{align*} \hat{p}^\mathrm{Chernoff}_\mathrm{u} & = \hat{p}\bigg(1+\frac{\log(2/\alpha)}{\hat{s}} + \sqrt{\frac{(\log(2/\alpha))^2}{\hat{s}^2}+\frac{2\log(2/\alpha)}{\hat{s}}}\bigg), \\[5pt] \hat{p}^\mathrm{Chernoff}_\mathrm{l} & = \hat{p}\bigg(1+\frac{\log(2/\alpha)}{2\hat{s}} - \sqrt{\frac{(\log(2/\alpha))^2}{4\hat{s}^2}+\frac{2\log(2/\alpha)}{\hat{s}}}\bigg).\end{align*}
\begin{align*} \hat{p}^\mathrm{Chernoff}_\mathrm{u} & = \hat{p}\bigg(1+\frac{\log(2/\alpha)}{\hat{s}} + \sqrt{\frac{(\log(2/\alpha))^2}{\hat{s}^2}+\frac{2\log(2/\alpha)}{\hat{s}}}\bigg), \\[5pt] \hat{p}^\mathrm{Chernoff}_\mathrm{l} & = \hat{p}\bigg(1+\frac{\log(2/\alpha)}{2\hat{s}} - \sqrt{\frac{(\log(2/\alpha))^2}{4\hat{s}^2}+\frac{2\log(2/\alpha)}{\hat{s}}}\bigg).\end{align*}
We highlight that in this case, the half-width of the Chernoff CI is of order
![]() $\Theta(\hat p/\sqrt{\hat{s}})$
, which scales in the same order as the CLT CI. If we check the difference between this interval and the CLT interval, we find that it is of the same order as the half-width of the CLT CI. The following theorem presents the details of this claim. We will shortly contrast this result with another one presented.
$\Theta(\hat p/\sqrt{\hat{s}})$
, which scales in the same order as the CLT CI. If we check the difference between this interval and the CLT interval, we find that it is of the same order as the half-width of the CLT CI. The following theorem presents the details of this claim. We will shortly contrast this result with another one presented.
Theorem 4. (Half-width of the Chernoff CI under the standard setting.)
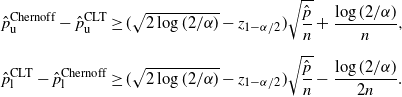 \begin{align*} \hat{p}_\mathrm{u}^\mathrm{Chernoff}-\hat{p}_\mathrm{u}^\mathrm{CLT} & \geq (\sqrt{2\log(2/\alpha)}-z_{1-\alpha/2})\sqrt{\frac{\hat{p}}{n}}+\frac{\log(2/\alpha)}{n}, \\[5pt] \hat{p}_\mathrm{l}^\mathrm{CLT}-\hat{p}_\mathrm{l}^\mathrm{Chernoff} & \geq (\sqrt{2\log(2/\alpha)}-z_{1-\alpha/2})\sqrt{\frac{\hat{p}}{n}}-\frac{\log(2/\alpha)}{2n}. \end{align*}
\begin{align*} \hat{p}_\mathrm{u}^\mathrm{Chernoff}-\hat{p}_\mathrm{u}^\mathrm{CLT} & \geq (\sqrt{2\log(2/\alpha)}-z_{1-\alpha/2})\sqrt{\frac{\hat{p}}{n}}+\frac{\log(2/\alpha)}{n}, \\[5pt] \hat{p}_\mathrm{l}^\mathrm{CLT}-\hat{p}_\mathrm{l}^\mathrm{Chernoff} & \geq (\sqrt{2\log(2/\alpha)}-z_{1-\alpha/2})\sqrt{\frac{\hat{p}}{n}}-\frac{\log(2/\alpha)}{2n}. \end{align*}
Note that
![]() $\sqrt{2\log(2/\alpha)}-z_{1-\alpha/2}>0$
for
$\sqrt{2\log(2/\alpha)}-z_{1-\alpha/2}>0$
for
![]() $0<\alpha<1$
.
$0<\alpha<1$
.
We recall that
![]() $1/n=\hat p/\hat{s}$
is of higher order than
$1/n=\hat p/\hat{s}$
is of higher order than
![]() $\sqrt{\hat p/\hat{s}}=\hat p/\sqrt{\hat{s}}$
. Provided that
$\sqrt{\hat p/\hat{s}}=\hat p/\sqrt{\hat{s}}$
. Provided that
![]() $\sqrt{2\log(2/\alpha)}-z_{1-\alpha/2}>0$
,
$\sqrt{2\log(2/\alpha)}-z_{1-\alpha/2}>0$
,
![]() $\hat{p}_\mathrm{u}^\mathrm{Chernoff}-\hat{p}_\mathrm{u}^\mathrm{CLT}$
(or
$\hat{p}_\mathrm{u}^\mathrm{Chernoff}-\hat{p}_\mathrm{u}^\mathrm{CLT}$
(or
![]() $\hat{p}_\mathrm{l}^\mathrm{Chernoff}-\hat{p}_\mathrm{l}^\mathrm{CLT}$
) is of no higher order than
$\hat{p}_\mathrm{l}^\mathrm{Chernoff}-\hat{p}_\mathrm{l}^\mathrm{CLT}$
) is of no higher order than
![]() $\hat{p}_\mathrm{u}^\mathrm{CLT}-\hat{p}$
(or
$\hat{p}_\mathrm{u}^\mathrm{CLT}-\hat{p}$
(or
![]() $\hat{p}_\mathrm{l}^\mathrm{CLT}-\hat{p}$
).
$\hat{p}_\mathrm{l}^\mathrm{CLT}-\hat{p}$
).
5.2.4. BE CI
We focus on the confidence upper bound as, unfortunately, we cannot derive a non-trivial confidence lower bound from (6) since any
![]() $0<p<\frac12$
such that
$0<p<\frac12$
such that
![]() $C/\sqrt{np(1-p)}\geq\alpha/2$
is contained in this confidence region. Now we further relax (6) to develop a more explicit upper bound. In particular, (6) could be relaxed to
$C/\sqrt{np(1-p)}\geq\alpha/2$
is contained in this confidence region. Now we further relax (6) to develop a more explicit upper bound. In particular, (6) could be relaxed to
In fact, for any
![]() $0\le\lambda\le1-({4C}/{\sqrt{n}\alpha})$
,
$0\le\lambda\le1-({4C}/{\sqrt{n}\alpha})$
,
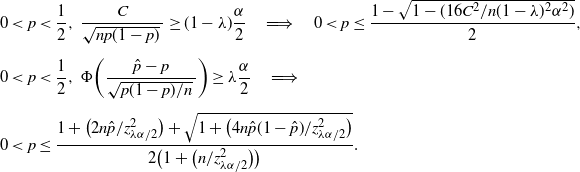 \begin{align*} & 0<p<\frac12,\ \frac{C}{\sqrt{np(1-p)}\,}\ge(1-\lambda)\frac{\alpha}{2} \quad \Longrightarrow \quad 0<p\le\frac{1-\sqrt{1-({16C^2}/{n(1-\lambda)^2\alpha^2})}}{2}, \\[5pt] &0<p<\frac12,\ \Phi\bigg(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}\,}\bigg)\ge\lambda\frac{\alpha}{2} \quad \Longrightarrow \\[5pt] & 0<p\le\frac{1+\big({2n\hat{p}}/{z_{\lambda\alpha/2}^2}\big) + \sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)}}{2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)}.\end{align*}
\begin{align*} & 0<p<\frac12,\ \frac{C}{\sqrt{np(1-p)}\,}\ge(1-\lambda)\frac{\alpha}{2} \quad \Longrightarrow \quad 0<p\le\frac{1-\sqrt{1-({16C^2}/{n(1-\lambda)^2\alpha^2})}}{2}, \\[5pt] &0<p<\frac12,\ \Phi\bigg(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}\,}\bigg)\ge\lambda\frac{\alpha}{2} \quad \Longrightarrow \\[5pt] & 0<p\le\frac{1+\big({2n\hat{p}}/{z_{\lambda\alpha/2}^2}\big) + \sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)}}{2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)}.\end{align*}
Therefore,
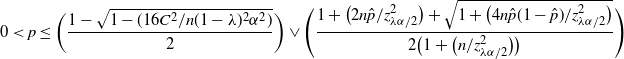 \begin{align*} 0<p\leq\bigg(\frac{1-\sqrt{1-({16C^2}/{n(1-\lambda)^2\alpha^2})}}{2}\bigg) \lor\Bigg(\frac{1+\big({2n\hat{p}}/{z_{\lambda\alpha/2}^2}\big) + \sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)}}{2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)}\Bigg)\end{align*}
\begin{align*} 0<p\leq\bigg(\frac{1-\sqrt{1-({16C^2}/{n(1-\lambda)^2\alpha^2})}}{2}\bigg) \lor\Bigg(\frac{1+\big({2n\hat{p}}/{z_{\lambda\alpha/2}^2}\big) + \sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)}}{2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)}\Bigg)\end{align*}
is a
![]() $(1-\alpha)$
-level CI. For simplicity, we denote the two parts as
$(1-\alpha)$
-level CI. For simplicity, we denote the two parts as
![]() $U_1$
and
$U_1$
and
![]() $U_2$
. Note that
$U_2$
. Note that
![]() $\lambda$
is not necessarily deterministic. Instead, it can be dependent on the data as long as it stays within the interval
$\lambda$
is not necessarily deterministic. Instead, it can be dependent on the data as long as it stays within the interval
![]() $[0,1-({4C}/{\sqrt{n}\alpha})]$
. In fact, we may choose
$[0,1-({4C}/{\sqrt{n}\alpha})]$
. In fact, we may choose
![]() $\lambda$
carefully such that
$\lambda$
carefully such that
![]() $U_1\leq U_2$
is guaranteed for sufficiently large n. Specifically, the following theorem proposes another valid CI.
$U_1\leq U_2$
is guaranteed for sufficiently large n. Specifically, the following theorem proposes another valid CI.
Theorem 5. (Relaxed BE CI under the standard setting.) Assume that
![]() $p<\frac12$
. Let
$p<\frac12$
. Let
![]() $\lambda = 1-({2\tilde{C}}/{\sqrt{n}\alpha})$
, where
$\lambda = 1-({2\tilde{C}}/{\sqrt{n}\alpha})$
, where
Here,
![]() $u<1$
is any constant such that
$u<1$
is any constant such that
![]() ${4C^2}/{u^2\alpha^2}<z_{(1-u)\alpha/2}^2$
. In the case that
${4C^2}/{u^2\alpha^2}<z_{(1-u)\alpha/2}^2$
. In the case that
![]() $\hat{p}=0$
or 1, naturally we set
$\hat{p}=0$
or 1, naturally we set
![]() $\tilde{C}=u\sqrt{n}\alpha/2$
. Then there exists
$\tilde{C}=u\sqrt{n}\alpha/2$
. Then there exists
![]() $N_0$
, which does not depend on p and
$N_0$
, which does not depend on p and
![]() $\hat{p}$
, such that, for any
$\hat{p}$
, such that, for any
![]() $n>N_0$
,
$n>N_0$
,
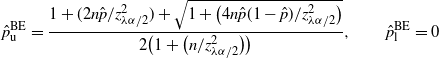 $$ \hat{p}_\mathrm{u}^\mathrm{BE} = \frac{1+({2n\hat{p}}/{z_{\lambda\alpha/2}^2})+\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)}} {2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)}, \qquad \hat{p}_\mathrm{l}^\mathrm{BE}=0 $$
$$ \hat{p}_\mathrm{u}^\mathrm{BE} = \frac{1+({2n\hat{p}}/{z_{\lambda\alpha/2}^2})+\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)}} {2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)}, \qquad \hat{p}_\mathrm{l}^\mathrm{BE}=0 $$
is a valid
![]() $(1-\alpha)$
-level CI for p. In particular,
$(1-\alpha)$
-level CI for p. In particular,
![]() $N_0$
can be chosen as
$N_0$
can be chosen as
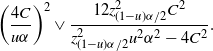 $$ \bigg(\frac{4C}{u\alpha}\bigg)^2 \lor \frac{12z_{(1-u)\alpha/2}^2C^2}{z_{(1-u)\alpha/2}^2u^2\alpha^2-4C^2}. $$
$$ \bigg(\frac{4C}{u\alpha}\bigg)^2 \lor \frac{12z_{(1-u)\alpha/2}^2C^2}{z_{(1-u)\alpha/2}^2u^2\alpha^2-4C^2}. $$
Actually,
![]() $\hat{p}_\mathrm{u}^\mathrm{BE}$
itself is a valid
$\hat{p}_\mathrm{u}^\mathrm{BE}$
itself is a valid
![]() $(1-\alpha/2)$
-level confidence upper bound for p, which is higher than the nominal level
$(1-\alpha/2)$
-level confidence upper bound for p, which is higher than the nominal level
![]() $1-\alpha$
. The series of relaxations makes this CI more and more conservative, but we will show that the upper bound still has a similar scale to
$1-\alpha$
. The series of relaxations makes this CI more and more conservative, but we will show that the upper bound still has a similar scale to
![]() $\hat{p}_\mathrm{u}^\mathrm{CLT}$
and
$\hat{p}_\mathrm{u}^\mathrm{CLT}$
and
![]() $\hat{p}_\mathrm{u}^\mathrm{Wilson}$
. Namely, we can derive that
$\hat{p}_\mathrm{u}^\mathrm{Wilson}$
. Namely, we can derive that
![]() $|\hat{p}_\mathrm{u}^\mathrm{BE}-\hat{p}_\mathrm{u}^\mathrm{CLT}|$
is bounded by order
$|\hat{p}_\mathrm{u}^\mathrm{BE}-\hat{p}_\mathrm{u}^\mathrm{CLT}|$
is bounded by order
![]() $1/n$
. In other words, though
$1/n$
. In other words, though
![]() $\hat{p}_\mathrm{u}^\mathrm{CLT}$
has undesirable coverage probability in the rare-event setting, it is not ‘too far’ from a valid upper bound. The following theorem states this result.
$\hat{p}_\mathrm{u}^\mathrm{CLT}$
has undesirable coverage probability in the rare-event setting, it is not ‘too far’ from a valid upper bound. The following theorem states this result.
Theorem 6. (Half-width of the BE CI under the standard setting.) Assume that
![]() $p<\frac12$
, abd
$p<\frac12$
, abd
![]() $\hat{p}_\mathrm{u}^\mathrm{BE}$
is as defined in Theorem 5. Then there is a constant
$\hat{p}_\mathrm{u}^\mathrm{BE}$
is as defined in Theorem 5. Then there is a constant
![]() $C_0$
, which does not depend on p and
$C_0$
, which does not depend on p and
![]() $\hat p$
, such that
$\hat p$
, such that
![]() $\big|\hat{p}_\mathrm{u}^\mathrm{BE}-\hat{p}_\mathrm{u}^\mathrm{CLT}\big| \leq C_0/n$
.
$\big|\hat{p}_\mathrm{u}^\mathrm{BE}-\hat{p}_\mathrm{u}^\mathrm{CLT}\big| \leq C_0/n$
.
Note that the bound in Theorem 6 can be rephrased as
![]() $\big|\hat{p}_\mathrm{u}^\mathrm{BE}-\hat{p}_\mathrm{u}^\mathrm{CLT}\big|\leq C_0\hat p/\hat{s}$
. In other words,
$\big|\hat{p}_\mathrm{u}^\mathrm{BE}-\hat{p}_\mathrm{u}^\mathrm{CLT}\big|\leq C_0\hat p/\hat{s}$
. In other words,
![]() $\hat p_\mathrm{u}^\mathrm{BE}$
differs from
$\hat p_\mathrm{u}^\mathrm{BE}$
differs from
![]() $\hat p_\mathrm{u}^\mathrm{CLT}$
by a higher order than the half-width of the CLT CI in terms of
$\hat p_\mathrm{u}^\mathrm{CLT}$
by a higher order than the half-width of the CLT CI in terms of
![]() $\hat{s}$
, while all quantities scale with
$\hat{s}$
, while all quantities scale with
![]() $\hat p$
in a similar manner. Compared to Theorem 4, we see in Theorem 6 that
$\hat p$
in a similar manner. Compared to Theorem 4, we see in Theorem 6 that
![]() $\hat p_\mathrm{u}^\mathrm{BE}$
is substantially tighter than
$\hat p_\mathrm{u}^\mathrm{BE}$
is substantially tighter than
![]() $\hat p_\mathrm{u}^\mathrm{Chernoff}$
when
$\hat p_\mathrm{u}^\mathrm{Chernoff}$
when
![]() $\hat{s}$
increases, although due to the implicit constant
$\hat{s}$
increases, although due to the implicit constant
![]() $C_0$
it may not be the case for small
$C_0$
it may not be the case for small
![]() $\hat{s}$
.
$\hat{s}$
.
6. Developments under targeted stopping
We now present our results for the targeted stopping setting, following the roadmap for the standard setting presented earlier. Namely, we first present the construction of the Chernoff and BE CIs (Section 6.1), followed by analyses of half-widths for all CIs (Section 6.2).
6.1. Derivation of new confidence intervals
To construct the new CIs under the targeted stopping setting, we again relax the confidence region (5) via Chernoff’s inequality and the BE theorem. Nevertheless, now we need to deal with the distribution of N instead of
![]() $\hat p$
as in (4). Hence, as we show below, the specific derivations of applying Chernoff’s inequality and the BE theorem differ from the standard setting.
$\hat p$
as in (4). Hence, as we show below, the specific derivations of applying Chernoff’s inequality and the BE theorem differ from the standard setting.
6.1.1. Chernoff CI
First, we propose a Chernoff CI similar to the one in the standard setting. By Markov’s inequality,
Then, for
![]() $x>n_0/p$
,
$x>n_0/p$
,
Similarly,
and thus, for
![]() $0<x<n_0/p$
,
$0<x<n_0/p$
,
Therefore,
![]() $F_N(N)\geq\alpha/2$
,
$F_N(N)\geq\alpha/2$
,
![]() $F_{N-}(N)\leq1-\alpha/2$
implies that
$F_{N-}(N)\leq1-\alpha/2$
implies that
Finally, we get that
is a valid
![]() $(1-\alpha)$
-level confidence region for p under the targeted stopping setting. After simplification, we summarize our result in the following theorem.
$(1-\alpha)$
-level confidence region for p under the targeted stopping setting. After simplification, we summarize our result in the following theorem.
Theorem 7. (Validity of the Chernoff CI under targeted stopping.) Suppose that we keep sampling from
![]() $\mathrm{Bernoulli}(p)$
until we get
$\mathrm{Bernoulli}(p)$
until we get
![]() $n_0$
successes, and the sample size is denoted by N. Then
$n_0$
successes, and the sample size is denoted by N. Then
is a valid
![]() $(1-\alpha)$
-level confidence region for p.
$(1-\alpha)$
-level confidence region for p.
It is easy to verify that
![]() $f(p)=p^{n_0}(1-p)^{N-n_0}-({\alpha}/{2})(n_0/N)^{n_0}(1-n_0/N)^{N-n_0}$
is increasing in
$f(p)=p^{n_0}(1-p)^{N-n_0}-({\alpha}/{2})(n_0/N)^{n_0}(1-n_0/N)^{N-n_0}$
is increasing in
![]() $[0,n_0/N]$
and decreasing in
$[0,n_0/N]$
and decreasing in
![]() $[n_0/N,1]$
. Moreover, we observe that
$[n_0/N,1]$
. Moreover, we observe that
![]() $f(0)=f(1)<0$
and
$f(0)=f(1)<0$
and
![]() $f(n_0/N)>0$
. Thus, (7) is actually an interval, and we could use the bisection method to numerically compute the bounds. Nevertheless, this CI is not as easy to study analytically as under the standard setting, so we will not include its half-width result in the following section.
$f(n_0/N)>0$
. Thus, (7) is actually an interval, and we could use the bisection method to numerically compute the bounds. Nevertheless, this CI is not as easy to study analytically as under the standard setting, so we will not include its half-width result in the following section.
6.1.2. BE CI
Now we apply the BE theorem again. We still assume that
![]() $p<\frac12$
is known a priori. By the theorem, we get
$p<\frac12$
is known a priori. By the theorem, we get
where
![]() $\sigma_N^2=\mathbb{E}(N_i-1/p)^2=(1-p)/p^2$
and
$\sigma_N^2=\mathbb{E}(N_i-1/p)^2=(1-p)/p^2$
and
![]() $\rho_N=E|N_i-1/p|^3$
.
$\rho_N=E|N_i-1/p|^3$
.
We need to deal with
![]() $\rho_N$
first. In fact, we know that
$\rho_N$
first. In fact, we know that
Since
![]() $N_i\sim \mathrm{Geometric}(p)$
, we know that
$N_i\sim \mathrm{Geometric}(p)$
, we know that
and thus
![]() $p^3\rho_N\le p^2-6p+6+3(2-p)+3+1=p^2-12p+16\le 16$
. Hence,
$p^3\rho_N\le p^2-6p+6+3(2-p)+3+1=p^2-12p+16\le 16$
. Hence,
where
![]() $C'=16C$
is an absolute constant.
$C'=16C$
is an absolute constant.
By setting
![]() $x=\sqrt{({p^2}/{n_0(1-p)})}(N-({n_0}/{p}))$
in (8) and
$x=\sqrt{({p^2}/{n_0(1-p)})}(N-({n_0}/{p}))$
in (8) and
![]() $x=\sqrt{({p^2}/{n_0(1-p)})}(({n_0}/{p})-N)$
in (9), we get
$x=\sqrt{({p^2}/{n_0(1-p)})}(({n_0}/{p})-N)$
in (9), we get
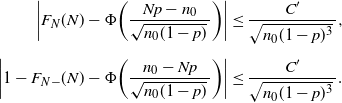 \begin{align*} \bigg|F_N(N)-\Phi\bigg(\frac{Np-n_0}{\sqrt{n_0(1-p)}\,}\bigg)\bigg| & \leq \frac{C'}{\sqrt{n_0(1-p)^3}\,}, \\[5pt] \bigg|1-F_{N-}(N)-\Phi\bigg(\frac{n_0-Np}{\sqrt{n_0(1-p)}\,}\bigg)\bigg| & \leq \frac{C'}{\sqrt{n_0(1-p)^3}\,}.\end{align*}
\begin{align*} \bigg|F_N(N)-\Phi\bigg(\frac{Np-n_0}{\sqrt{n_0(1-p)}\,}\bigg)\bigg| & \leq \frac{C'}{\sqrt{n_0(1-p)^3}\,}, \\[5pt] \bigg|1-F_{N-}(N)-\Phi\bigg(\frac{n_0-Np}{\sqrt{n_0(1-p)}\,}\bigg)\bigg| & \leq \frac{C'}{\sqrt{n_0(1-p)^3}\,}.\end{align*}
Hence,
![]() $F_N(N)\geq\alpha/2$
,
$F_N(N)\geq\alpha/2$
,
![]() $F_{N-}(N)\leq 1-\alpha/2$
implies that
$F_{N-}(N)\leq 1-\alpha/2$
implies that
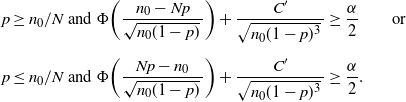 \begin{align*} p\geq n_0/N\text{ and }\Phi\bigg(\frac{n_0-Np}{\sqrt{n_0(1-p)}\,}\bigg)+\frac{C'}{\sqrt{n_0(1-p)^3}\,} & \geq \frac{\alpha}{2} \qquad \text{or} \\[5pt] p\leq n_0/N\text{ and }\Phi\bigg(\frac{Np-n_0}{\sqrt{n_0(1-p)}\,}\bigg)+\frac{C'}{\sqrt{n_0(1-p)^3}\,} & \geq \frac{\alpha}{2}.\end{align*}
\begin{align*} p\geq n_0/N\text{ and }\Phi\bigg(\frac{n_0-Np}{\sqrt{n_0(1-p)}\,}\bigg)+\frac{C'}{\sqrt{n_0(1-p)^3}\,} & \geq \frac{\alpha}{2} \qquad \text{or} \\[5pt] p\leq n_0/N\text{ and }\Phi\bigg(\frac{Np-n_0}{\sqrt{n_0(1-p)}\,}\bigg)+\frac{C'}{\sqrt{n_0(1-p)^3}\,} & \geq \frac{\alpha}{2}.\end{align*}
Thus, we have developed a valid confidence region under this particular setting that is similar to the one in Section 5.
Theorem 8. (Validity of the BE CI under targeted stopping.) Suppose that we keep sampling from
![]() $\mathrm{Bernoulli}(p)$
until we get
$\mathrm{Bernoulli}(p)$
until we get
![]() $n_0$
successes, and the sample size is denoted by N. Assume that
$n_0$
successes, and the sample size is denoted by N. Assume that
![]() $p<\frac12$
. Then
$p<\frac12$
. Then
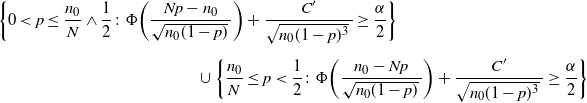 \begin{multline} \bigg\{0<p\leq\frac{n_0}{N}\wedge\frac12\colon \Phi\bigg(\frac{Np-n_0}{\sqrt{n_0(1-p)}\,}\bigg) + \frac{C'}{\sqrt{n_0(1-p)^3}\,} \geq \frac{\alpha}{2}\bigg\} \\[5pt] \cup \bigg\{\frac{n_0}{N}\leq p<\frac{1}{2} \colon \Phi\bigg(\frac{n_0-Np}{\sqrt{n_0(1-p)}\,}\bigg) + \frac{C'}{\sqrt{n_0(1-p)^3}\,} \geq \frac{\alpha}{2}\bigg\} \end{multline}
\begin{multline} \bigg\{0<p\leq\frac{n_0}{N}\wedge\frac12\colon \Phi\bigg(\frac{Np-n_0}{\sqrt{n_0(1-p)}\,}\bigg) + \frac{C'}{\sqrt{n_0(1-p)^3}\,} \geq \frac{\alpha}{2}\bigg\} \\[5pt] \cup \bigg\{\frac{n_0}{N}\leq p<\frac{1}{2} \colon \Phi\bigg(\frac{n_0-Np}{\sqrt{n_0(1-p)}\,}\bigg) + \frac{C'}{\sqrt{n_0(1-p)^3}\,} \geq \frac{\alpha}{2}\bigg\} \end{multline}
is a valid
![]() $(1-\alpha)$
-level confidence region for p. Here, C′ is a universal constant. In particular, we can pick
$(1-\alpha)$
-level confidence region for p. Here, C′ is a universal constant. In particular, we can pick
![]() $C'=16C$
, where C is the constant in the BE theorem.
$C'=16C$
, where C is the constant in the BE theorem.
Note that when
![]() $n_0$
is not large enough, we have
$n_0$
is not large enough, we have
![]() $C'/\sqrt{n_0(1-p)^3}\geq\alpha/2$
anyway. That is to say, this confidence region is not really practical. However, it could still provide an insight into how close the CLT or Wilson intervals are to a valid one.
$C'/\sqrt{n_0(1-p)^3}\geq\alpha/2$
anyway. That is to say, this confidence region is not really practical. However, it could still provide an insight into how close the CLT or Wilson intervals are to a valid one.
6.2. Analyses of half-widths
As mentioned before, under the targeted stopping setting, the Chernoff CI is no longer easy to analyze. Thus, in this subsection we only cover the analyses for the CLT, Wilson, and BE CIs. For the first two, as the formulas of the CIs are the same as the standard setting, we simply present the results here. For the BE CI, the main idea of the derivations is similar to the standard setting, but there are differences in the technical details. In particular, we are now able to get a non-trivial lower bound.
6.2.1. CLT and Wilson CIs
Under the targeted stopping setting, the formulas of the CLT and Wilson CIs are the same as under the standard setting with
![]() $\hat p=n_0/N$
. Thus, clearly we still have that
$\hat p=n_0/N$
. Thus, clearly we still have that
![]() $\hat{p}_{\mathrm{u},n_0}^\mathrm{CLT}-\hat{p}=\hat{p}-\hat{p}_{\mathrm{l},n_0}^\mathrm{CLT}=\Theta(\hat{p}/\sqrt{n_0})=\Theta(\sqrt{n_0}/N)$
, and that
$\hat{p}_{\mathrm{u},n_0}^\mathrm{CLT}-\hat{p}=\hat{p}-\hat{p}_{\mathrm{l},n_0}^\mathrm{CLT}=\Theta(\hat{p}/\sqrt{n_0})=\Theta(\sqrt{n_0}/N)$
, and that
![]() $\big|\hat{p}_{\mathrm{u},n_0}^\mathrm{Wilson}-\hat{p}_{\mathrm{u},n_0}^\mathrm{CLT}\big|=O(1/N)=O(\hat p/n_0)$
,
$\big|\hat{p}_{\mathrm{u},n_0}^\mathrm{Wilson}-\hat{p}_{\mathrm{u},n_0}^\mathrm{CLT}\big|=O(1/N)=O(\hat p/n_0)$
,
![]() $\big|\hat{p}_{\mathrm{l},n_0}^\mathrm{Wilson}-\hat{p}_{\mathrm{l},n_0}^\mathrm{CLT}\big|=O(1/N)=O(\hat p/n_0)$
.
$\big|\hat{p}_{\mathrm{l},n_0}^\mathrm{Wilson}-\hat{p}_{\mathrm{l},n_0}^\mathrm{CLT}\big|=O(1/N)=O(\hat p/n_0)$
.
6.2.2. BE CI
Similar to Section 5, the confidence region (10) could be further relaxed. However, unlike in the standard setting, now the error term
![]() $C'/\sqrt{n_0(1-p)^3}$
could be well controlled for tiny p and as a result we are able to get a non-trivial lower bound in this case. More concretely, for any
$C'/\sqrt{n_0(1-p)^3}$
could be well controlled for tiny p and as a result we are able to get a non-trivial lower bound in this case. More concretely, for any
![]() $0<\lambda<1$
,
$0<\lambda<1$
,
If we could find
![]() $0<\lambda<1$
such that
$0<\lambda<1$
such that
![]() $({4C'^2}/{n_0(1-\lambda)^2\alpha^2})^{1/3}=\frac12$
then, for any
$({4C'^2}/{n_0(1-\lambda)^2\alpha^2})^{1/3}=\frac12$
then, for any
![]() $0<p<\frac12$
,
$0<p<\frac12$
,
As a result, any p in (10) must satisfy
After simplification, we get
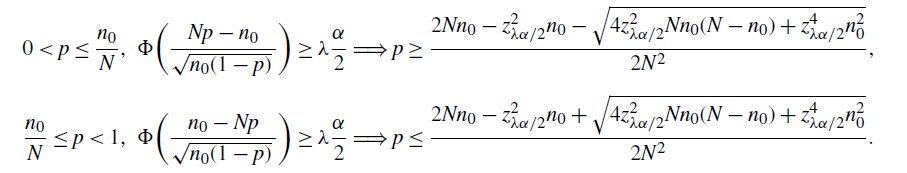 \begin{align*} 0<p\leq\frac{n_0}{N},\ \Phi\bigg(\frac{Np-n_0}{\sqrt{n_0(1-p)}\,}\bigg)\geq\lambda\frac{\alpha}{2} & \Longrightarrow p\geq\frac{2Nn_0-z_{\lambda\alpha/2}^2n_0-\sqrt{4z_{\lambda\alpha/2}^2Nn_0(N-n_0)+z_{\lambda\alpha/2}^4n_0^2}}{2N^2}, \\[5pt] \frac{n_0}{N}\leq p<1,\ \Phi\bigg(\frac{n_0-Np}{\sqrt{n_0(1-p)}\,}\bigg)\geq\lambda\frac{\alpha}{2} & \Longrightarrow p\leq\frac{2Nn_0-z_{\lambda\alpha/2}^2n_0+\sqrt{4z_{\lambda\alpha/2}^2Nn_0(N-n_0)+z_{\lambda\alpha/2}^4n_0^2}}{2N^2}.\end{align*}
\begin{align*} 0<p\leq\frac{n_0}{N},\ \Phi\bigg(\frac{Np-n_0}{\sqrt{n_0(1-p)}\,}\bigg)\geq\lambda\frac{\alpha}{2} & \Longrightarrow p\geq\frac{2Nn_0-z_{\lambda\alpha/2}^2n_0-\sqrt{4z_{\lambda\alpha/2}^2Nn_0(N-n_0)+z_{\lambda\alpha/2}^4n_0^2}}{2N^2}, \\[5pt] \frac{n_0}{N}\leq p<1,\ \Phi\bigg(\frac{n_0-Np}{\sqrt{n_0(1-p)}\,}\bigg)\geq\lambda\frac{\alpha}{2} & \Longrightarrow p\leq\frac{2Nn_0-z_{\lambda\alpha/2}^2n_0+\sqrt{4z_{\lambda\alpha/2}^2Nn_0(N-n_0)+z_{\lambda\alpha/2}^4n_0^2}}{2N^2}.\end{align*}
Thus, (10) could be relaxed into a valid
![]() $(1-\alpha)$
-level CI, which is defined more rigorously in the following theorem.
$(1-\alpha)$
-level CI, which is defined more rigorously in the following theorem.
Theorem 9. (Relaxed BE CI under targeted stopping.) Suppose that we keep sampling from
![]() $\mathrm{Bernoulli}(p)$
until we get
$\mathrm{Bernoulli}(p)$
until we get
![]() $n_0$
successes, and the sample size is denoted by N. Assume that
$n_0$
successes, and the sample size is denoted by N. Assume that
![]() $p<\frac12$
. Let
$p<\frac12$
. Let
![]() $\lambda=1-({4\sqrt{2}C'}/{\sqrt{n_0}\alpha})$
. Then, for any
$\lambda=1-({4\sqrt{2}C'}/{\sqrt{n_0}\alpha})$
. Then, for any
![]() $n_0>32C'^2/\alpha^2$
,
$n_0>32C'^2/\alpha^2$
,
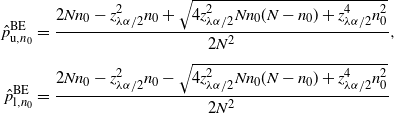 \begin{align*} \hat{p}_{\mathrm{u},n_0}^\mathrm{BE} & = \frac{2Nn_0-z_{\lambda\alpha/2}^2n_0+\sqrt{4z_{\lambda\alpha/2}^2Nn_0(N-n_0)+z_{\lambda\alpha/2}^4n_0^2}}{2N^2}, \\[5pt] \hat{p}_{\mathrm{l},n_0}^\mathrm{BE} & = \frac{2Nn_0-z_{\lambda\alpha/2}^2n_0-\sqrt{4z_{\lambda\alpha/2}^2Nn_0(N-n_0)+z_{\lambda\alpha/2}^4n_0^2}}{2N^2} \end{align*}
\begin{align*} \hat{p}_{\mathrm{u},n_0}^\mathrm{BE} & = \frac{2Nn_0-z_{\lambda\alpha/2}^2n_0+\sqrt{4z_{\lambda\alpha/2}^2Nn_0(N-n_0)+z_{\lambda\alpha/2}^4n_0^2}}{2N^2}, \\[5pt] \hat{p}_{\mathrm{l},n_0}^\mathrm{BE} & = \frac{2Nn_0-z_{\lambda\alpha/2}^2n_0-\sqrt{4z_{\lambda\alpha/2}^2Nn_0(N-n_0)+z_{\lambda\alpha/2}^4n_0^2}}{2N^2} \end{align*}
is a valid
![]() $(1-\alpha)$
-level CI for p. Here, C′ is the same as in Theorem 8.
$(1-\alpha)$
-level CI for p. Here, C′ is the same as in Theorem 8.
Finally, like in the standard setting, we will compare the difference between the BE and CLT CIs.
Theorem 10. (Half-width of the BE CI under targeted stopping.) Assume that
![]() $p<\frac12$
, and that
$p<\frac12$
, and that
![]() $\hat{p}_{\mathrm{u},n_0}^\mathrm{BE}$
and
$\hat{p}_{\mathrm{u},n_0}^\mathrm{BE}$
and
![]() $\hat{p}_{\mathrm{l},n_0}^\mathrm{BE}$
are as defined in Theorem 9. Then there is a constant
$\hat{p}_{\mathrm{l},n_0}^\mathrm{BE}$
are as defined in Theorem 9. Then there is a constant
![]() $C'_{\!\!0}$
, which does not depend on p and N, such that
$C'_{\!\!0}$
, which does not depend on p and N, such that
![]() $\hat{p}_{\mathrm{u},n_0}^\mathrm{BE}-\hat{p}_{\mathrm{u},n_0}^\mathrm{CLT} \leq C'_{\!\!0}/N$
and
$\hat{p}_{\mathrm{u},n_0}^\mathrm{BE}-\hat{p}_{\mathrm{u},n_0}^\mathrm{CLT} \leq C'_{\!\!0}/N$
and
![]() $\hat{p}_{\mathrm{l},n_0}^\mathrm{CLT}-\hat{p}_{\mathrm{l},n_0}^\mathrm{BE} \leq C'_{\!\!0}/N$
.
$\hat{p}_{\mathrm{l},n_0}^\mathrm{CLT}-\hat{p}_{\mathrm{l},n_0}^\mathrm{BE} \leq C'_{\!\!0}/N$
.
Therefore, under the targeted stopping setting, we could justify that the CLT CI is not too far from a valid one in terms of both upper and lower bounds.
7. Numerical experiments
To close the paper, we perform some numerical experiments to visualize the differences among the CIs.
7.1. Experiments under the standard setting
The true value is chosen as
![]() $p=10^{-6}$
. For each of the settings
$p=10^{-6}$
. For each of the settings
![]() $n=5/p$
,
$n=5/p$
,
![]() $10/p$
,
$10/p$
,
![]() $30/p$
,
$30/p$
,
![]() $50/p$
, and
$50/p$
, and
![]() $100/p$
we conduct 100 000 experimental repetitions and calculate the CIs with
$100/p$
we conduct 100 000 experimental repetitions and calculate the CIs with
![]() $\alpha=0.05$
. Figure 3 and Table 3 respectively present the average values of the confidence upper and lower bounds from the 100 000 repetitions and the coverage probabilities of the five CIs covered in this paper.
$\alpha=0.05$
. Figure 3 and Table 3 respectively present the average values of the confidence upper and lower bounds from the 100 000 repetitions and the coverage probabilities of the five CIs covered in this paper.

Figure 3. Average values of the confidence upper and lower bounds under the standard setting.
As analyzed in Section 5.2, when np is large the CIs scale similarly, except that BE fails to give a non-zero lower bound. While the CLT interval is closest to the truth in terms of the mean value of the upper bound, it is not reliable, especially when np is small. For instance, when
![]() $np=5$
, its coverage probability is only
$np=5$
, its coverage probability is only
![]() $0.858$
, which is much lower than the nominal confidence level of
$0.858$
, which is much lower than the nominal confidence level of
![]() $0.95$
. The Wilson and exact CIs are quite similar, especially for the upper bound. However, we notice that the Wilson bound sometimes fails to achieve the nominal confidence level, but the error in the coverage probability is acceptable to some extent. The Chernoff and BE CIs are conservative, as expected, since they further relax the conservative confidence region (4). We would like to point out that though the BE upper bound seems to be much larger than the Chernoff, it decays much faster as np increases, which coincides with Theorems 4 and 6.
$0.95$
. The Wilson and exact CIs are quite similar, especially for the upper bound. However, we notice that the Wilson bound sometimes fails to achieve the nominal confidence level, but the error in the coverage probability is acceptable to some extent. The Chernoff and BE CIs are conservative, as expected, since they further relax the conservative confidence region (4). We would like to point out that though the BE upper bound seems to be much larger than the Chernoff, it decays much faster as np increases, which coincides with Theorems 4 and 6.
7.2. Experiments under targeted stopping
Now we consider the targeted stopping setting. We again set
![]() $p=10^{-6}$
. For each of the settings
$p=10^{-6}$
. For each of the settings
![]() $n_0=5,10,30,50,100$
we conduct 100 000 experimental repetitions and calculate the CIs with
$n_0=5,10,30,50,100$
we conduct 100 000 experimental repetitions and calculate the CIs with
![]() $\alpha=0.05$
. Figure 4 and Table 4 respectively present the average values of the confidence upper and lower bounds from the 100 000 repetitions and the coverage probabilities of the CIs. Note that we do not include the BE CI since it is trivial due to the small
$\alpha=0.05$
. Figure 4 and Table 4 respectively present the average values of the confidence upper and lower bounds from the 100 000 repetitions and the coverage probabilities of the CIs. Note that we do not include the BE CI since it is trivial due to the small
![]() $n_0$
, as aforementioned.
$n_0$
, as aforementioned.
Table 3. Coverage probabilities of the CIs under the standard setting.
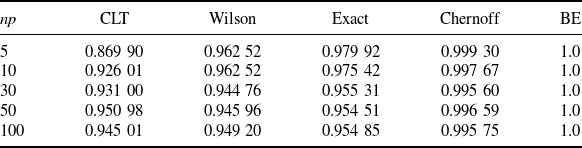
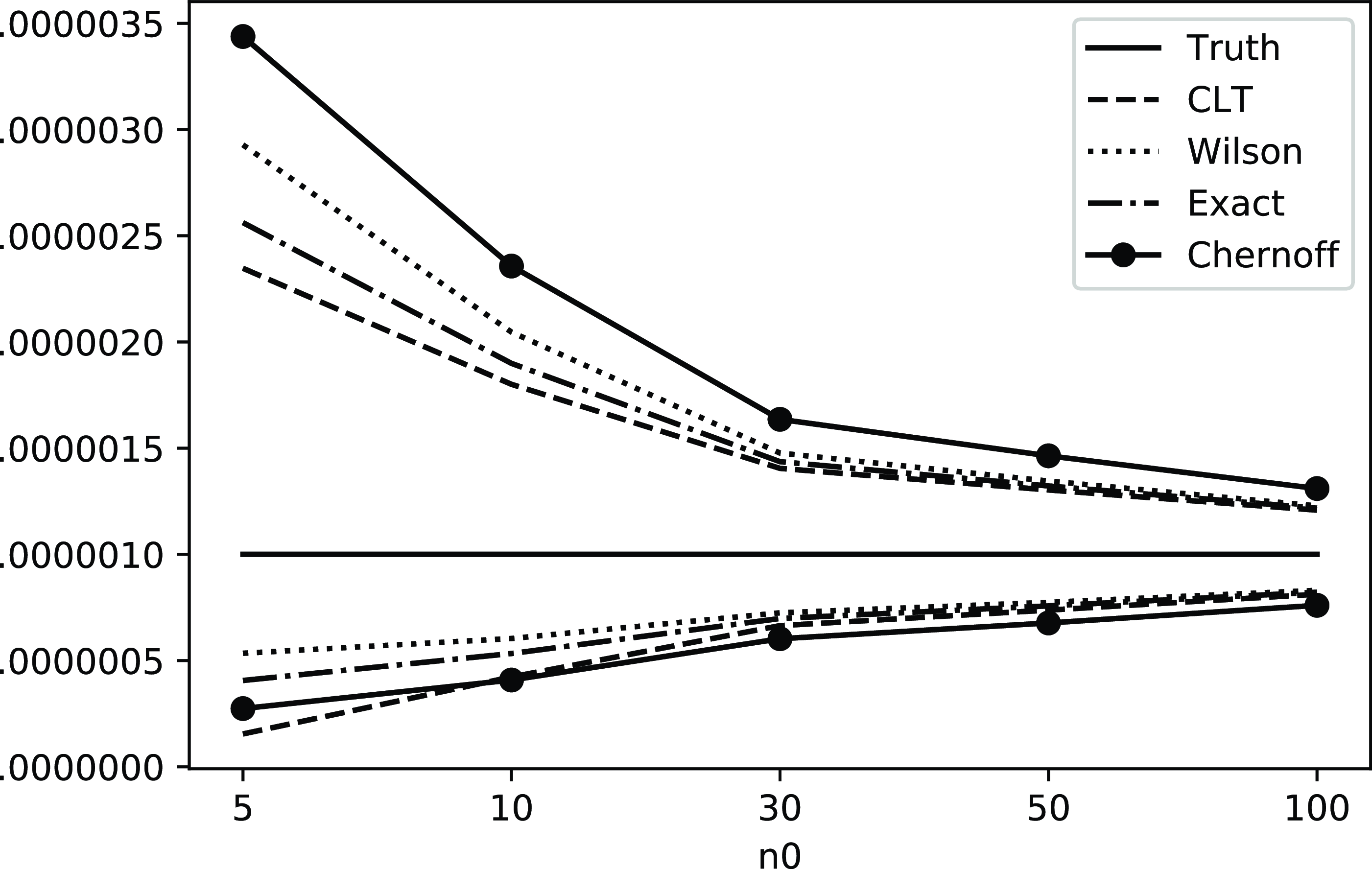
Figure 4. Average values of the confidence upper and lower bounds under the targeted stopping setting.
The Chernoff CI is still conservative, as expected, since it further relaxes the conservative confidence region (5). We focus on comparing the other three CIs. From Figure 4 we see that, for the upper bound, the CLT bound is the closest to the truth and the Wilson bound is the farthest. For the lower bound, the Wilson bound is the closest and the CLT bound is the farthest. The exact bound falls in between. On the other hand, they all have a similar magnitude, and when
![]() $n_0$
is large they are all close to each other. In terms of coverage probability (Table 4), the three CIs also have similar performance when
$n_0$
is large they are all close to each other. In terms of coverage probability (Table 4), the three CIs also have similar performance when
![]() $n_0$
is large. In particular, in relation to the motivation in Section 2, if we can sample until we observe enough (say 30) successes, then the CLT CI is indeed reliable to use, although it is not guaranteed to be valid.
$n_0$
is large. In particular, in relation to the motivation in Section 2, if we can sample until we observe enough (say 30) successes, then the CLT CI is indeed reliable to use, although it is not guaranteed to be valid.
8. Conclusion
In this paper we have studied the uncertainty quantification, more precisely the construction, validity, and tightness of CIs, for rare-event probability using naive sample proportion estimators from Bernoulli data. We focused on two settings, the standard setting where the sample size is fixed, and the targeted stopping setting where the number of successes is fixed. Under each setting, we first reviewed the existing CLT, Wilson, and exact CIs. It is known that the CLT and Wilson CIs are not necessarily valid in the sense that the coverage probability can be lower than the nominal confidence level, and the exact CI is valid yet its tightness is hard to analyze. These motivated us to derive other valid CIs with more explicit expressions. More specifically, we relaxed the exact confidence region via inverting Chernoff’s inequality and the BE theorem to obtain Chernoff and BE CIs, respectively. Tables 1 and 2 in Section 4 provide a comprehensive summary of our findings, and we briefly summarized our key findings in Section 4.
Table 4. Coverage probabilities of the CIs under the targeted stopping setting.
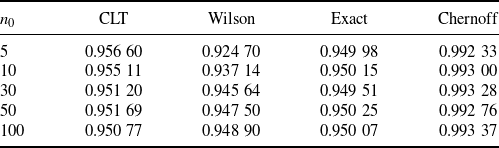
Overall, we recommend the exact CI when we want to ensure a guarantee of the nominal confidence level, otherwise we suggest using the Wilson CI, given its excellent empirical performance. Moreover, in either the standard setting or the targeted stopping setting, we have justified that the CLT CI is not far from the valid Chernoff and BE CIs, so it also exhibits reasonable tightness in terms of half-width. However, its coverage probability can deviate significantly from the nominal level when np is small. The latter two intervals are conservative and hence not recommended for use in practice, but they provide useful insights in understanding that the CLT and Wilson CIs are relatively close to these two valid CIs.
Appendix A. Proofs
Proof of Theorem
3. We get directly from the formula for
![]() $\hat{p}_\mathrm{u}^\mathrm{Wilson}$
that
$\hat{p}_\mathrm{u}^\mathrm{Wilson}$
that
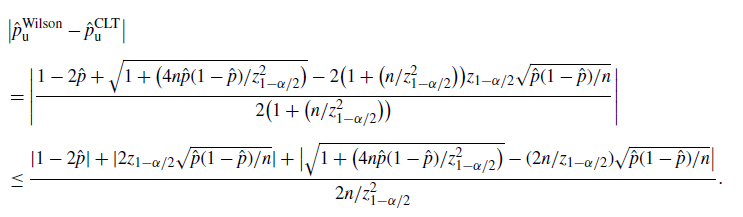 \begin{align*} & \big|\hat{p}_\mathrm{u}^\mathrm{Wilson}-\hat{p}_\mathrm{u}^\mathrm{CLT}\big| \\[5pt] & = \Bigg|\frac{1-2\hat{p}+\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{1-\alpha/2}^2}\big)} - 2\big(1+\big({n}/{z_{1-\alpha/2}^2}\big)\big)z_{1-\alpha/2}\sqrt{{\hat{p}(1-\hat{p})}/{n}}} {2\big(1+\big({n}/{z_{1-\alpha/2}^2}\big)\big)}\Bigg| \\[5pt] & \leq \frac{|1-2\hat{p}| + |2z_{1-\alpha/2}\sqrt{{\hat{p}(1-\hat{p})}/{n}}| + \big|\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{1-\alpha/2}^2}\big)} - ({2n}/{z_{1-\alpha/2}})\sqrt{{\hat{p}(1-\hat{p})}/{n}}\big|}{2n/z_{1-\alpha/2}^2}. \end{align*}
\begin{align*} & \big|\hat{p}_\mathrm{u}^\mathrm{Wilson}-\hat{p}_\mathrm{u}^\mathrm{CLT}\big| \\[5pt] & = \Bigg|\frac{1-2\hat{p}+\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{1-\alpha/2}^2}\big)} - 2\big(1+\big({n}/{z_{1-\alpha/2}^2}\big)\big)z_{1-\alpha/2}\sqrt{{\hat{p}(1-\hat{p})}/{n}}} {2\big(1+\big({n}/{z_{1-\alpha/2}^2}\big)\big)}\Bigg| \\[5pt] & \leq \frac{|1-2\hat{p}| + |2z_{1-\alpha/2}\sqrt{{\hat{p}(1-\hat{p})}/{n}}| + \big|\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{1-\alpha/2}^2}\big)} - ({2n}/{z_{1-\alpha/2}})\sqrt{{\hat{p}(1-\hat{p})}/{n}}\big|}{2n/z_{1-\alpha/2}^2}. \end{align*}
We have that
![]() $|1-2\hat{p}|\leq 1$
,
$|1-2\hat{p}|\leq 1$
,
![]() $|2z_{1-\alpha/2}\sqrt{\hat{p}(1-\hat{p})/n}|\leq z_{1-\alpha/2}/\sqrt{n}$
, and
$|2z_{1-\alpha/2}\sqrt{\hat{p}(1-\hat{p})/n}|\leq z_{1-\alpha/2}/\sqrt{n}$
, and
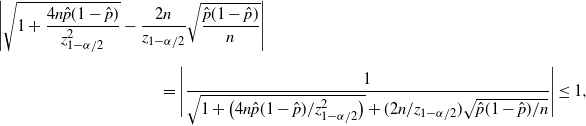 \begin{multline*} \Bigg|\sqrt{1+\frac{4n\hat{p}(1-\hat{p})}{z_{1-\alpha/2}^2}} - \frac{2n}{z_{1-\alpha/2}}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\Bigg| \\[5pt] = \Bigg|\frac{1}{\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{1-\alpha/2}^2}\big)} + ({2n}/{z_{1-\alpha/2}})\sqrt{{\hat{p}(1-\hat{p})}/{n}}}\Bigg| \leq 1, \end{multline*}
\begin{multline*} \Bigg|\sqrt{1+\frac{4n\hat{p}(1-\hat{p})}{z_{1-\alpha/2}^2}} - \frac{2n}{z_{1-\alpha/2}}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\Bigg| \\[5pt] = \Bigg|\frac{1}{\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{1-\alpha/2}^2}\big)} + ({2n}/{z_{1-\alpha/2}})\sqrt{{\hat{p}(1-\hat{p})}/{n}}}\Bigg| \leq 1, \end{multline*}
which concludes the proof for the upper bounds. The proof for the lower bound is almost the same.
Proof of Theorem 4. We have
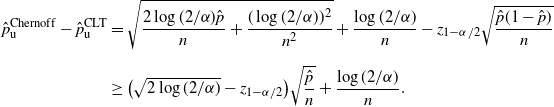 \begin{align*} \hat{p}_\mathrm{u}^\mathrm{Chernoff}-\hat{p}_\mathrm{u}^\mathrm{CLT} & = \sqrt{\frac{2\log(2/\alpha)\hat{p}}{n}+\frac{(\log(2/\alpha))^2}{n^2}} + \frac{\log(2/\alpha)}{n} - z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \\[5pt] & \geq \big(\sqrt{2\log(2/\alpha)}-z_{1-\alpha/2}\big)\sqrt{\frac{\hat{p}}{n}} + \frac{\log(2/\alpha)}{n}. \end{align*}
\begin{align*} \hat{p}_\mathrm{u}^\mathrm{Chernoff}-\hat{p}_\mathrm{u}^\mathrm{CLT} & = \sqrt{\frac{2\log(2/\alpha)\hat{p}}{n}+\frac{(\log(2/\alpha))^2}{n^2}} + \frac{\log(2/\alpha)}{n} - z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \\[5pt] & \geq \big(\sqrt{2\log(2/\alpha)}-z_{1-\alpha/2}\big)\sqrt{\frac{\hat{p}}{n}} + \frac{\log(2/\alpha)}{n}. \end{align*}
Similarly, we could prove the inequality for the lower bounds.
Proof of Theorem
5. Following our derivations, it suffices to show that, for the given
![]() $N_0$
and any
$N_0$
and any
![]() $n>N_0$
,
$n>N_0$
,
![]() $0\leq\lambda\leq 1-({4C}/{\sqrt{n}\alpha})$
and
$0\leq\lambda\leq 1-({4C}/{\sqrt{n}\alpha})$
and
![]() $U_1\leq U_2$
. Obviously,
$U_1\leq U_2$
. Obviously,
![]() ${2\tilde{C}}/{\sqrt{n}\alpha}\leq u<1$
, so
${2\tilde{C}}/{\sqrt{n}\alpha}\leq u<1$
, so
![]() $\lambda>0$
. On the other side,
$\lambda>0$
. On the other side,
![]() $\lambda\leq 1-({4C}/{\sqrt{n}\alpha})$
holds since
$\lambda\leq 1-({4C}/{\sqrt{n}\alpha})$
holds since
![]() $n\geq({4C}/{u\alpha})^2$
.
$n\geq({4C}/{u\alpha})^2$
.
Now we prove that
![]() $U_1\leq U_2$
for
$U_1\leq U_2$
for
![]() $n>N_0$
. Indeed, if
$n>N_0$
. Indeed, if
![]() $\tilde{C}=C/\sqrt{\hat{p}(1-\hat{p})}$
, then
$\tilde{C}=C/\sqrt{\hat{p}(1-\hat{p})}$
, then
![]() $U_1=\hat{p}\land(1-\hat{p})\le \hat{p}$
and we know that
$U_1=\hat{p}\land(1-\hat{p})\le \hat{p}$
and we know that
![]() $U_2\ge\hat{p}$
, so
$U_2\ge\hat{p}$
, so
![]() $U_1\le U_2$
. In the other case that
$U_1\le U_2$
. In the other case that
![]() $\tilde{C}=u\sqrt{n}\alpha/2$
, we have
$\tilde{C}=u\sqrt{n}\alpha/2$
, we have
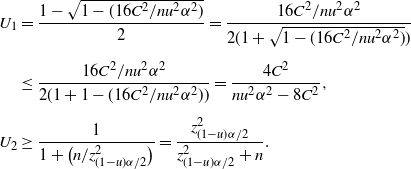 \begin{align*} U_1 & = \frac{1-\sqrt{1-({16C^2}/{nu^2\alpha^2})}}{2} = \frac{{16C^2}/{nu^2\alpha^2}}{2(1+\sqrt{1-({16C^2}/{nu^2\alpha^2})})} \\[5pt] & \leq \frac{{16C^2}/{nu^2\alpha^2}}{2(1+1-({16C^2}/{nu^2\alpha^2}))} = \frac{4C^2}{nu^2\alpha^2-8C^2}, \\[5pt] U_2 & \ge \frac{1}{1+\big({n}/{z_{(1-u)\alpha/2}^2}\big)} = \frac{z_{(1-u)\alpha/2}^2}{z_{(1-u)\alpha/2}^2+n}. \end{align*}
\begin{align*} U_1 & = \frac{1-\sqrt{1-({16C^2}/{nu^2\alpha^2})}}{2} = \frac{{16C^2}/{nu^2\alpha^2}}{2(1+\sqrt{1-({16C^2}/{nu^2\alpha^2})})} \\[5pt] & \leq \frac{{16C^2}/{nu^2\alpha^2}}{2(1+1-({16C^2}/{nu^2\alpha^2}))} = \frac{4C^2}{nu^2\alpha^2-8C^2}, \\[5pt] U_2 & \ge \frac{1}{1+\big({n}/{z_{(1-u)\alpha/2}^2}\big)} = \frac{z_{(1-u)\alpha/2}^2}{z_{(1-u)\alpha/2}^2+n}. \end{align*}
Since u is chosen such that
![]() ${4C^2}/{u^2\alpha^2}<z_{(1-u)\alpha/2}^2$
and
${4C^2}/{u^2\alpha^2}<z_{(1-u)\alpha/2}^2$
and
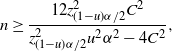 $$ n\geq \frac{12z_{(1-u)\alpha/2}^2C^2}{z_{(1-u)\alpha/2}^2u^2\alpha^2-4C^2}, $$
$$ n\geq \frac{12z_{(1-u)\alpha/2}^2C^2}{z_{(1-u)\alpha/2}^2u^2\alpha^2-4C^2}, $$
we get
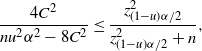 $$ \frac{4C^2}{nu^2\alpha^2-8C^2}\leq \frac{z_{(1-u)\alpha/2}^2}{z_{(1-u)\alpha/2}^2+n}, $$
$$ \frac{4C^2}{nu^2\alpha^2-8C^2}\leq \frac{z_{(1-u)\alpha/2}^2}{z_{(1-u)\alpha/2}^2+n}, $$
and hence
![]() $U_1\leq U_2$
. Note that as
$U_1\leq U_2$
. Note that as
![]() $u\uparrow 1$
,
$u\uparrow 1$
,
![]() ${4C^2}/{u^2\alpha^2}\rightarrow{4C^2}/{\alpha^2}$
while
${4C^2}/{u^2\alpha^2}\rightarrow{4C^2}/{\alpha^2}$
while
![]() $z_{(1-u)\alpha/2}^2\rightarrow\infty$
, and thus such a u exists.
$z_{(1-u)\alpha/2}^2\rightarrow\infty$
, and thus such a u exists.
Proof of Theorem 6. We have
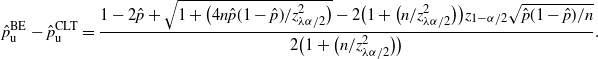 $$ \hat{p}_\mathrm{u}^\mathrm{BE}-\hat{p}_\mathrm{u}^\mathrm{CLT} = \frac{1-2\hat{p}+\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)} - 2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)z_{1-\alpha/2}\sqrt{{\hat{p}(1-\hat{p})}/{n}}} {2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)}. $$
$$ \hat{p}_\mathrm{u}^\mathrm{BE}-\hat{p}_\mathrm{u}^\mathrm{CLT} = \frac{1-2\hat{p}+\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)} - 2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)z_{1-\alpha/2}\sqrt{{\hat{p}(1-\hat{p})}/{n}}} {2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)}. $$
We first deal with
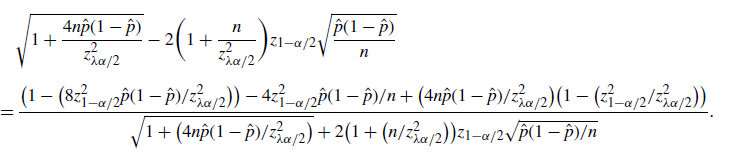 \begin{multline*} \sqrt{1+\frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}} - 2\bigg(1+\frac{n}{z_{\lambda\alpha/2}^2}\bigg)z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \\[5pt] = \frac{\big(1-\big({8z_{1-\alpha/2}^2\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)\big) - {4z_{1-\alpha/2}^2\hat{p}(1-\hat{p})}/{n} + \big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big) \big(1-\big({z_{1-\alpha/2}^2}/{z_{\lambda\alpha/2}^2}\big)\big)} {\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)} + 2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)z_{1-\alpha/2}\sqrt{{\hat{p}(1-\hat{p})}/{n}}}. \end{multline*}
\begin{multline*} \sqrt{1+\frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}} - 2\bigg(1+\frac{n}{z_{\lambda\alpha/2}^2}\bigg)z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \\[5pt] = \frac{\big(1-\big({8z_{1-\alpha/2}^2\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)\big) - {4z_{1-\alpha/2}^2\hat{p}(1-\hat{p})}/{n} + \big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big) \big(1-\big({z_{1-\alpha/2}^2}/{z_{\lambda\alpha/2}^2}\big)\big)} {\sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha/2}^2}\big)} + 2\big(1+\big({n}/{z_{\lambda\alpha/2}^2}\big)\big)z_{1-\alpha/2}\sqrt{{\hat{p}(1-\hat{p})}/{n}}}. \end{multline*}
The denominator satisfies
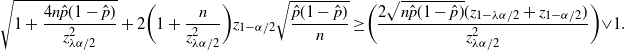 $$ \sqrt{1+\frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}} + 2\bigg(1+\frac{n}{z_{\lambda\alpha/2}^2}\bigg)z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \ge \! \bigg(\frac{2\sqrt{n\hat{p}(1-\hat{p})}(z_{1-\lambda\alpha/2}+z_{1-\alpha/2})}{z_{\lambda\alpha/2}^2}\bigg) \!\lor\! 1.$$
$$ \sqrt{1+\frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}} + 2\bigg(1+\frac{n}{z_{\lambda\alpha/2}^2}\bigg)z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \ge \! \bigg(\frac{2\sqrt{n\hat{p}(1-\hat{p})}(z_{1-\lambda\alpha/2}+z_{1-\alpha/2})}{z_{\lambda\alpha/2}^2}\bigg) \!\lor\! 1.$$
Note that
![]() $(z_{1-\lambda\alpha/2}+z_{1-\alpha/2})/z_{\lambda\alpha/2}^2$
increases with the value of
$(z_{1-\lambda\alpha/2}+z_{1-\alpha/2})/z_{\lambda\alpha/2}^2$
increases with the value of
![]() $\lambda$
. Since
$\lambda$
. Since
![]() $\lambda\ge 1-u>0$
, we can find a constant
$\lambda\ge 1-u>0$
, we can find a constant
![]() $C_1$
such that
$C_1$
such that
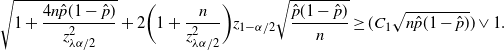 $$ \sqrt{1+\frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}} + 2\bigg(1+\frac{n}{z_{\lambda\alpha/2}^2}\bigg)z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \ge (C_1\sqrt{n\hat{p}(1-\hat{p})}) \lor 1. $$
$$ \sqrt{1+\frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}} + 2\bigg(1+\frac{n}{z_{\lambda\alpha/2}^2}\bigg)z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \ge (C_1\sqrt{n\hat{p}(1-\hat{p})}) \lor 1. $$
Then we deal with the numerator. We know that
![]() $z_{\alpha/2}=\Phi^{-1}(\alpha/2)$
and
$z_{\alpha/2}=\Phi^{-1}(\alpha/2)$
and
![]() $z_{\lambda\alpha/2}=\Phi^{-1}(\lambda\alpha/2)$
. By Taylor expansion, we have
$z_{\lambda\alpha/2}=\Phi^{-1}(\lambda\alpha/2)$
. By Taylor expansion, we have
Here,
![]() $r(\lambda)$
is continuous in
$r(\lambda)$
is continuous in
![]() $\lambda$
and
$\lambda$
and
![]() $r(\lambda)/(1-\lambda)\to 0$
as
$r(\lambda)/(1-\lambda)\to 0$
as
![]() $\lambda\uparrow 1$
. We also know that
$\lambda\uparrow 1$
. We also know that
![]() $1-\lambda\le u$
, and thus
$1-\lambda\le u$
, and thus
![]() $|r(\lambda)/(1-\lambda)|=|(\sqrt{n}\alpha r(\lambda))/(2\tilde{C})|$
is bounded by a constant. Hence,
$|r(\lambda)/(1-\lambda)|=|(\sqrt{n}\alpha r(\lambda))/(2\tilde{C})|$
is bounded by a constant. Hence,
![]() $|\sqrt{n\hat{p}(1-\hat{p})}r(\lambda)|$
is bounded by a constant. We have
$|\sqrt{n\hat{p}(1-\hat{p})}r(\lambda)|$
is bounded by a constant. We have
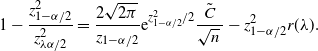 $$ 1-\frac{z_{1-\alpha/2}^2}{z_{\lambda\alpha/2}^2} = \frac{2\sqrt{2\pi}}{z_{1-\alpha/2}} {\mathrm{e}}^{{z_{1-\alpha/2}^2}/{2}}\frac{\tilde{C}}{\sqrt{n}\,}-z_{1-\alpha/2}^2r(\lambda). $$
$$ 1-\frac{z_{1-\alpha/2}^2}{z_{\lambda\alpha/2}^2} = \frac{2\sqrt{2\pi}}{z_{1-\alpha/2}} {\mathrm{e}}^{{z_{1-\alpha/2}^2}/{2}}\frac{\tilde{C}}{\sqrt{n}\,}-z_{1-\alpha/2}^2r(\lambda). $$
Thus, the numerator satisfies
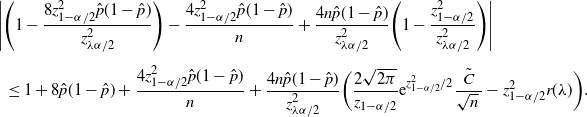 \begin{multline*} \Bigg|\Bigg(1-\frac{8z_{1-\alpha/2}^2\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}\Bigg) - \frac{4z_{1-\alpha/2}^2\hat{p}(1-\hat{p})}{n} + \frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}\Bigg(1-\frac{z_{1-\alpha/2}^2}{z_{\lambda\alpha/2}^2}\Bigg)\Bigg| \\[5pt] \le 1 + 8\hat{p}(1-\hat{p}) + \frac{4z_{1-\alpha/2}^2\hat{p}(1-\hat{p})}{n} + \frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2} \bigg(\frac{2\sqrt{2\pi}}{z_{1-\alpha/2}}{\mathrm{e}}^{{z_{1-\alpha/2}^2}/{2}}\frac{\tilde{C}}{\sqrt{n}\,} - z_{1-\alpha/2}^2r(\lambda)\bigg). \end{multline*}
\begin{multline*} \Bigg|\Bigg(1-\frac{8z_{1-\alpha/2}^2\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}\Bigg) - \frac{4z_{1-\alpha/2}^2\hat{p}(1-\hat{p})}{n} + \frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}\Bigg(1-\frac{z_{1-\alpha/2}^2}{z_{\lambda\alpha/2}^2}\Bigg)\Bigg| \\[5pt] \le 1 + 8\hat{p}(1-\hat{p}) + \frac{4z_{1-\alpha/2}^2\hat{p}(1-\hat{p})}{n} + \frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2} \bigg(\frac{2\sqrt{2\pi}}{z_{1-\alpha/2}}{\mathrm{e}}^{{z_{1-\alpha/2}^2}/{2}}\frac{\tilde{C}}{\sqrt{n}\,} - z_{1-\alpha/2}^2r(\lambda)\bigg). \end{multline*}
Clearly, the first three terms divided by the denominator are bounded by some constants. Now we consider the fourth term. Since
![]() $|\sqrt{n\hat{p}(1-\hat{p})}r(\lambda)|$
is bounded, we can also get that the fourth term divided by the denominator is bounded by some universal constant.
$|\sqrt{n\hat{p}(1-\hat{p})}r(\lambda)|$
is bounded, we can also get that the fourth term divided by the denominator is bounded by some universal constant.
Therefore, combining the above results, we know that
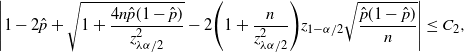 $$ \Bigg|1 - 2\hat{p} + \sqrt{1+\frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}} - 2\Bigg(1+\frac{n}{z_{\lambda\alpha/2}^2}\Bigg)z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\Bigg| \le C_2, $$
$$ \Bigg|1 - 2\hat{p} + \sqrt{1+\frac{4n\hat{p}(1-\hat{p})}{z_{\lambda\alpha/2}^2}} - 2\Bigg(1+\frac{n}{z_{\lambda\alpha/2}^2}\Bigg)z_{1-\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\Bigg| \le C_2, $$
where
![]() $C_2$
is a positive constant. We also have
$C_2$
is a positive constant. We also have
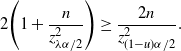 $$ 2\Bigg(1+\frac{n}{z_{\lambda\alpha/2}^2}\Bigg)\ge \frac{2n}{z_{(1-u)\alpha/2}^2}. $$
$$ 2\Bigg(1+\frac{n}{z_{\lambda\alpha/2}^2}\Bigg)\ge \frac{2n}{z_{(1-u)\alpha/2}^2}. $$
Hence, the error term satisfies
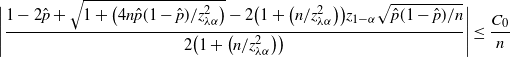 $$ \Bigg|\frac{1 - 2\hat{p} + \sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha}^2}\big)} - 2\big(1+\big({n}/{z_{\lambda\alpha}^2}\big)\big)z_{1-\alpha}\sqrt{{\hat{p}(1-\hat{p})}/{n}}} {2\big(1+\big({n}/{z_{\lambda\alpha}^2}\big)\big)}\Bigg| \le \frac{C_0}{n} $$
$$ \Bigg|\frac{1 - 2\hat{p} + \sqrt{1+\big({4n\hat{p}(1-\hat{p})}/{z_{\lambda\alpha}^2}\big)} - 2\big(1+\big({n}/{z_{\lambda\alpha}^2}\big)\big)z_{1-\alpha}\sqrt{{\hat{p}(1-\hat{p})}/{n}}} {2\big(1+\big({n}/{z_{\lambda\alpha}^2}\big)\big)}\Bigg| \le \frac{C_0}{n} $$
for some constant
![]() $C_0$
. From the above derivations, we find that
$C_0$
. From the above derivations, we find that
![]() $C_0$
only depends on
$C_0$
only depends on
![]() $\alpha$
and the choice of u.
$\alpha$
and the choice of u.
Proof of Theorem
9. If
![]() $n_0>32C'^2/\alpha^2$
, then
$n_0>32C'^2/\alpha^2$
, then
![]() $0<\lambda<1$
. The validness of the CI is justified by the derivations above the theorem.
$0<\lambda<1$
. The validness of the CI is justified by the derivations above the theorem.
Proof of Theorem 10. We have
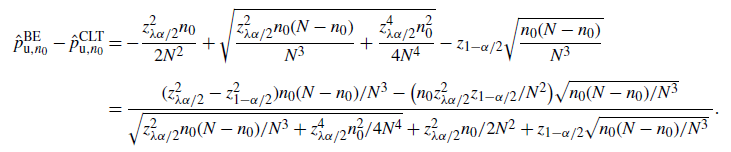 \begin{align*} \hat{p}_{\mathrm{u},n_0}^\mathrm{BE} - \hat{p}_{\mathrm{u},n_0}^\mathrm{CLT} & = -\frac{z_{\lambda\alpha/2}^2n_0}{2N^2} + \sqrt{\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3}+\frac{z_{\lambda\alpha/2}^4n_0^2}{4N^4}} - z_{1-\alpha/2}\sqrt{\frac{n_0(N-n_0)}{N^3}} \\[5pt] & = \frac{{(z_{\lambda\alpha/2}^2-z_{1-\alpha/2}^2)n_0(N-n_0)}/{N^3} - \big({n_0z_{\lambda\alpha/2}^2z_{1-\alpha/2}}/{N^2}\big)\sqrt{{n_0(N-n_0)}/{N^3}}} {\sqrt{{z_{\lambda\alpha/2}^2n_0(N-n_0)}/{N^3} + {z_{\lambda\alpha/2}^4n_0^2}/{4N^4}} + {z_{\lambda\alpha/2}^2n_0}/{2N^2} + z_{1-\alpha/2}\sqrt{{n_0(N-n_0)}/{N^3}}\,}. \end{align*}
\begin{align*} \hat{p}_{\mathrm{u},n_0}^\mathrm{BE} - \hat{p}_{\mathrm{u},n_0}^\mathrm{CLT} & = -\frac{z_{\lambda\alpha/2}^2n_0}{2N^2} + \sqrt{\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3}+\frac{z_{\lambda\alpha/2}^4n_0^2}{4N^4}} - z_{1-\alpha/2}\sqrt{\frac{n_0(N-n_0)}{N^3}} \\[5pt] & = \frac{{(z_{\lambda\alpha/2}^2-z_{1-\alpha/2}^2)n_0(N-n_0)}/{N^3} - \big({n_0z_{\lambda\alpha/2}^2z_{1-\alpha/2}}/{N^2}\big)\sqrt{{n_0(N-n_0)}/{N^3}}} {\sqrt{{z_{\lambda\alpha/2}^2n_0(N-n_0)}/{N^3} + {z_{\lambda\alpha/2}^4n_0^2}/{4N^4}} + {z_{\lambda\alpha/2}^2n_0}/{2N^2} + z_{1-\alpha/2}\sqrt{{n_0(N-n_0)}/{N^3}}\,}. \end{align*}
First, for the denominator:
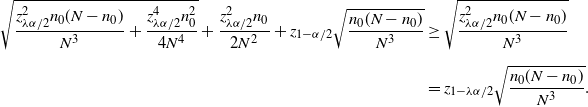 \begin{align*} \sqrt{\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3} + \frac{z_{\lambda\alpha/2}^4n_0^2}{4N^4}} + \frac{z_{\lambda\alpha/2}^2n_0}{2N^2} + z_{1-\alpha/2}\sqrt{\frac{n_0(N-n_0)}{N^3}} & \geq \sqrt{\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3}} \\[5pt] & = z_{1-\lambda\alpha/2}\sqrt{\frac{n_0(N-n_0)}{N^3}}. \end{align*}
\begin{align*} \sqrt{\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3} + \frac{z_{\lambda\alpha/2}^4n_0^2}{4N^4}} + \frac{z_{\lambda\alpha/2}^2n_0}{2N^2} + z_{1-\alpha/2}\sqrt{\frac{n_0(N-n_0)}{N^3}} & \geq \sqrt{\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3}} \\[5pt] & = z_{1-\lambda\alpha/2}\sqrt{\frac{n_0(N-n_0)}{N^3}}. \end{align*}
Next, for the numerator:
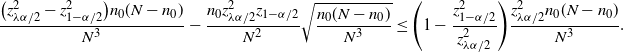 \begin{equation*} \frac{\big(z_{\lambda\alpha/2}^2-z_{1-\alpha/2}^2\big)n_0(N-n_0)}{N^3} - \frac{n_0z_{\lambda\alpha/2}^2z_{1-\alpha/2}}{N^2}\sqrt{\frac{n_0(N-n_0)}{N^3}} \leq \Bigg(1-\frac{z_{1-\alpha/2}^2}{z_{\lambda\alpha/2}^2}\Bigg)\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3}. \end{equation*}
\begin{equation*} \frac{\big(z_{\lambda\alpha/2}^2-z_{1-\alpha/2}^2\big)n_0(N-n_0)}{N^3} - \frac{n_0z_{\lambda\alpha/2}^2z_{1-\alpha/2}}{N^2}\sqrt{\frac{n_0(N-n_0)}{N^3}} \leq \Bigg(1-\frac{z_{1-\alpha/2}^2}{z_{\lambda\alpha/2}^2}\Bigg)\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3}. \end{equation*}
As mentioned in the proof of Theorem 6, we have
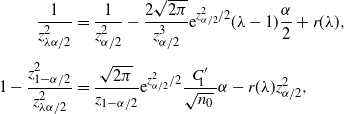 \begin{align*} \frac{1}{z_{\lambda\alpha/2}^2} & = \frac{1}{z_{\alpha/2}^2} - \frac{2\sqrt{2\pi}}{z_{\alpha/2}^3}{\mathrm{e}}^{{z_{\alpha/2}^2}/{2}} (\lambda-1)\frac{\alpha}{2} + r(\lambda), \\[5pt] 1 - \frac{z_{1-\alpha/2}^2}{z_{\lambda\alpha/2}^2} & = \frac{\sqrt{2\pi}}{z_{1-\alpha/2}}{\mathrm{e}}^{{z_{\alpha/2}^2}/{2}}\frac{C'_{\!\!1}}{\sqrt{n_0}\,}\alpha - r(\lambda)z_{\alpha/2}^2, \end{align*}
\begin{align*} \frac{1}{z_{\lambda\alpha/2}^2} & = \frac{1}{z_{\alpha/2}^2} - \frac{2\sqrt{2\pi}}{z_{\alpha/2}^3}{\mathrm{e}}^{{z_{\alpha/2}^2}/{2}} (\lambda-1)\frac{\alpha}{2} + r(\lambda), \\[5pt] 1 - \frac{z_{1-\alpha/2}^2}{z_{\lambda\alpha/2}^2} & = \frac{\sqrt{2\pi}}{z_{1-\alpha/2}}{\mathrm{e}}^{{z_{\alpha/2}^2}/{2}}\frac{C'_{\!\!1}}{\sqrt{n_0}\,}\alpha - r(\lambda)z_{\alpha/2}^2, \end{align*}
where
![]() $r(\lambda)$
is continuous in
$r(\lambda)$
is continuous in
![]() $\lambda$
and
$\lambda$
and
![]() $r(\lambda)/(1-\lambda)\to 0$
as
$r(\lambda)/(1-\lambda)\to 0$
as
![]() $\lambda\uparrow 1$
. We know that
$\lambda\uparrow 1$
. We know that
![]() $1-\lambda=C'_{\!\!1}/\sqrt{n_0}$
for some constant
$1-\lambda=C'_{\!\!1}/\sqrt{n_0}$
for some constant
![]() $C'_{\!\!1}>0$
from the choice of
$C'_{\!\!1}>0$
from the choice of
![]() $\lambda$
. For
$\lambda$
. For
![]() $n_0>32C'^2/\alpha^2$
,
$n_0>32C'^2/\alpha^2$
,
![]() $\lambda$
is bounded away from 0, and hence
$\lambda$
is bounded away from 0, and hence
![]() $|r(\lambda)/(1-\lambda)|=|\sqrt{n_0}r(\lambda)/C'_{\!\!1}|$
has a constant upper bound. Hence, there exists a constant
$|r(\lambda)/(1-\lambda)|=|\sqrt{n_0}r(\lambda)/C'_{\!\!1}|$
has a constant upper bound. Hence, there exists a constant
![]() $C'_{\!\!2}>0$
such that
$C'_{\!\!2}>0$
such that
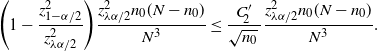 \begin{equation*} \Bigg(1-\frac{z_{1-\alpha/2}^2}{z_{\lambda\alpha/2}^2}\Bigg)\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3} \leq \frac{C'_{\!\!2}}{\sqrt{n_0}\,}\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3}. \end{equation*}
\begin{equation*} \Bigg(1-\frac{z_{1-\alpha/2}^2}{z_{\lambda\alpha/2}^2}\Bigg)\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3} \leq \frac{C'_{\!\!2}}{\sqrt{n_0}\,}\frac{z_{\lambda\alpha/2}^2n_0(N-n_0)}{N^3}. \end{equation*}
Combining the results, we get
where
![]() $C'_{\!\!3}>0$
is a constant and we get the last inequality since
$C'_{\!\!3}>0$
is a constant and we get the last inequality since
![]() $\lambda$
has a non-zero lower bound.
$\lambda$
has a non-zero lower bound.
Now notice that
![]() $\hat{p}_{\mathrm{l},n_0}^\mathrm{CLT} - \hat{p}_{\mathrm{l},n_0}^\mathrm{BE} = \hat{p}_{\mathrm{u},n_0}^\mathrm{BE} - \hat{p}_{\mathrm{u},n_0}^\mathrm{CLT} + {z_{\lambda\alpha/2}^2n_0}/{N^2}$
and
$\hat{p}_{\mathrm{l},n_0}^\mathrm{CLT} - \hat{p}_{\mathrm{l},n_0}^\mathrm{BE} = \hat{p}_{\mathrm{u},n_0}^\mathrm{BE} - \hat{p}_{\mathrm{u},n_0}^\mathrm{CLT} + {z_{\lambda\alpha/2}^2n_0}/{N^2}$
and
![]() ${z_{\lambda\alpha/2}^2n_0}/{N^2} \leq {z_{\lambda\alpha/2}^2}/{N} = O(1/N)$
. Therefore, we could find a constant
${z_{\lambda\alpha/2}^2n_0}/{N^2} \leq {z_{\lambda\alpha/2}^2}/{N} = O(1/N)$
. Therefore, we could find a constant
![]() $C'_{\!\!0}$
such that the theorem holds.
$C'_{\!\!0}$
such that the theorem holds.
Acknowledgements
We thank the associate editor and referees for their helpful suggestions that have greatly improved this paper. A preliminary conference version of this work has appeared in [Reference Bai and Lam8].
Funding information
We gratefully acknowledge support from the National Science Foundation under grants CAREER CMMI-1834710 and IIS-1849280.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
















