Hostname: page-component-5c6d5d7d68-vt8vv Total loading time: 0.001 Render date: 2024-08-16T14:37:26.288Z Has data issue: false hasContentIssue false
  • English
  • Français

An unambiguous definition of the Froude number for lee waves in the deep ocean

Published online by Cambridge University Press:  20 October 2017

F. T. Mayer Open the ORCID record for F. T. Mayer [Opens in a new window]  and
O. B. Fringer
F. T. Mayer*
Affiliation:
The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
O. B. Fringer
Affiliation:
The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: fmayer@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

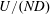There is a long-standing debate in the literature of stratified flows over topography concerning the correct dimensionless number to refer to as a Froude number. Common definitions using external quantities of the flow include $U/(ND)$, 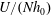$U/(Nh_{0})$, and 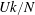$Uk/N$, where 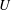$U$ and 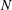$N$ are, respectively, scales for the background velocity and buoyancy frequency, 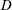$D$ is the depth, and 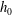$h_{0}$ and 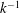$k^{-1}$ are, respectively, height and width scales of the topography. It is also possible to define an internal Froude number 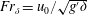$Fr_{\unicode[STIX]{x1D6FF}}=u_{0}/\sqrt{g^{\prime }\unicode[STIX]{x1D6FF}}$, where 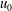$u_{0}$, 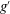$g^{\prime }$, and 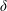$\unicode[STIX]{x1D6FF}$ are, respectively, the characteristic velocity, reduced gravity, and vertical length scale of the perturbation above the topography. For the case of hydrostatic lee waves in a deep ocean, both 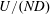$U/(ND)$ and 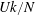$Uk/N$ are insignificantly small, rendering the dimensionless number 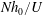$Nh_{0}/U$ the only relevant dynamical parameter. However, although it appears to be an inverse Froude number, such an interpretation is incorrect. By non-dimensionalizing the stratified Euler equations describing the flow of an infinitely deep fluid over topography, we show that 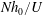$Nh_{0}/U$ is in fact the square of the internal Froude number because it can identically be written in terms of the inner variables, 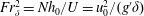$Fr_{\unicode[STIX]{x1D6FF}}^{2}=Nh_{0}/U=u_{0}^{2}/(g^{\prime }\unicode[STIX]{x1D6FF})$. Our scaling also identifies 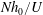$Nh_{0}/U$ as the ratio of the vertical velocity scale within the lee wave to the group velocity of the lee wave, which we term the vertical Froude number, $Fr_{vert}=Nh_{0}/U=w_{0}/c_{g}$. To encapsulate such behaviour, we suggest referring to 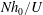$Nh_{0}/U$ as the lee-wave Froude number, 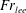$Fr_{lee}$.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Topographic effects
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , R3
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afanasyev, Y. D. & Peltier, W. R. 1998 The three-dimensionalization of stratified flow over two-dimensional topography. J. Atmos. Sci. 55 (1), 19–39.2.0.CO;2>CrossRefGoogle Scholar
Aguilar, D. A. & Sutherland, B. R. 2006 Internal wave generation from rough topography. Phys. Fluids 18 (6), 1–9.CrossRefGoogle Scholar
Armi, L. 1986 The hydraulics of two flowing layers with different densities. J. Fluid Mech. 163, 27–58.CrossRefGoogle Scholar
Baines, P. G. 1995 Topographic Effects in Stratified Flows. Cambridge University Press.Google Scholar
Clark, T. L. & Peltier, W. R. 1984 Critical level reflection and the resonant growth of nonlinear mountain waves. J. Atmos. Sci. 41 (21), 3122–3134.2.0.CO;2>CrossRefGoogle Scholar
Crook, N. A., Clark, T. L. & Moncrieff, M. W. 1990 The Denver cyclone. Part I: generation in low Froude number flow. J. Atmos. Sci. 47 (23), 2725–2742.2.0.CO;2>CrossRefGoogle Scholar
Drazin, P. G. 1961 On the steady flow of a fluid of variable density past an obstacle. Tellus 13 (2), 239–251.CrossRefGoogle Scholar
Durran, D. R. 1986 Another look at downslope windstorms. Part I: the development of analogs to supercritical flow in an infinitely deep, continuously stratified fluid. J. Atmos. Sci. 43 (21), 2527–2543.2.0.CO;2>CrossRefGoogle Scholar
Eckermann, S. D., Lindeman, J., Broutman, D., Ma, J. & Boybeyi, Z. 2010 Momentum fluxes of gravity waves generated by variable Froude number flow over three-dimensional obstacles. J. Atmos. Sci. 67 (7), 2260–2278.CrossRefGoogle Scholar
Farmer, D. M. & Armi, L. 1986 Maximal two-layer exchange over a sill and through the combination of a sill and contraction with barotropic flow. J. Fluid Mech. 164, 53–76.CrossRefGoogle Scholar
Farmer, D. M. & Smith, J. D. 1980 Tidal interaction of stratified flow with a sill in Knight Inlet. Deep-Sea Res. 27, 239–254.CrossRefGoogle Scholar
Garrett, C. & Kunze, E. 2007 Internal tide generation in the deep ocean. Annu. Rev. Fluid Mech. 39, 57–87.CrossRefGoogle Scholar
Gill, A. E. 1982 Atmosphere-Ocean Dynamics. Academic Press.Google Scholar
Kimura, F. & Manins, P. 1988 Blocking in periodic valleys. Boundary-Layer Meteorol. 44 (1), 137–169.CrossRefGoogle Scholar
Kitabayashi, K. 1977 Wind tunnel and field studies of stagnant flow upstream of a ridge. J. Met. Soc. Japan 55 (2), 193–204.Google Scholar
Klymak, J. M., Legg, S. M. & Pinkel, R. 2010 High-mode stationary waves in stratified flow over large obstacles. J. Fluid Mech. 644, 321–336.CrossRefGoogle Scholar
Laprise, R. & Peltier, W. R. 1989a The linear stability of nonlinear mountain waves: implications for the understanding of severe downslope windstorms. J. Atmos. Sci. 46 (4), 545–564.Google Scholar
Laprise, R. & Peltier, W. R. 1989b On the structural characteristics of steady finite-amplitude mountain waves over bell-shaped topography. J. Atmos. Sci. 46 (4), 586–595.2.0.CO;2>CrossRefGoogle Scholar
Laprise, R. & Peltier, W. R. 1989c The structure and energetics of transient eddies in a numerical simulation of breaking mountain waves. J. Atmos. Sci. 46 (4), 565–585.Google Scholar
Legg, S. & Klymak, J. 2008 Internal hydraulic jumps and overturning generated by tidal flow over a tall steep ridge. J. Phys. Oceanogr. 38, 1949–1964.CrossRefGoogle Scholar
Long, R. R. 1953 Some aspects of the flow of stratified fluids I. A theoretical investigation. Tellus V, 42–58.CrossRefGoogle Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10 (04), 496–508.CrossRefGoogle Scholar
Miles, J. W. 1969 Waves and wave drag in stratified flows. In Applied Mechanics. International Union of Theoretical and Applied Mechanics (ed. Vincenti, W. G. & Hetnyi, M.), pp. 50–75. Springer.Google Scholar
Nikurashin, M. & Ferrari, R. 2010 Radiation and dissipation of internal waves generated by geostrophic motions impinging on small-scale topography: theory. J. Phys. Oceanogr. 40 (5), 1055–1074.CrossRefGoogle Scholar
Peltier, W. R. & Clark, T. L. 1983 Nonlinear mountain waves in two and three spatial dimensions. Q. J. R. Meteorol. Soc. 109 (461), 527–548.CrossRefGoogle Scholar
Scinocca, J. F. & Peltier, W. R. 1994 Finite-amplitude wave-activity diagnostics for Long’s stationary solution. J. Atmos. Sci. 51 (4), 613–622.2.0.CO;2>CrossRefGoogle Scholar
Smith, R. B. 1989 Mountain-induced stagnation points in hydrostatic flow. Tellus A 41 (3), 270–274.CrossRefGoogle Scholar
Smolarkiewicz, P. K. & Rotunno, R. 1989 Low Froude number flow past three-dimensional obstacles. Part I: baroclinically generated Lee vortices. J. Atmos. Sci. 46 (8), 1154–1164.2.0.CO;2>CrossRefGoogle Scholar
Welch, W. T., Smolarkiewicz, P., Rotunno, R. & Boville, B. A. 2001 The large-scale effects of flow over periodic mesoscale topography. J. Atmos. Sci. 58 (12), 1477–1492.2.0.CO;2>CrossRefGoogle Scholar
Winters, K. B. & Armi, L. 2012 Hydraulic control of continuously stratified flow over an obstacle. J. Fluid Mech. 700, 502–513.CrossRefGoogle Scholar