Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-18T18:20:05.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Application of the compressible 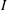$I$-dependent rheology to chute and shear flow instabilities

Published online by Cambridge University Press:  14 February 2019

J. S. Fannon Open the ORCID record for J. S. Fannon [Opens in a new window] ,
I. R. Moyles  and
A. C. Fowler
J. S. Fannon*
Affiliation:
MACSI, University of Limerick, Limerick, V94 T9PX, Ireland
I. R. Moyles
Affiliation:
MACSI, University of Limerick, Limerick, V94 T9PX, Ireland Department of Mathematics and Statistics, York University, Toronto, ON M3J 1P3, Canada
A. C. Fowler
Affiliation:
MACSI, University of Limerick, Limerick, V94 T9PX, Ireland OCIAM, University of Oxford, Oxford, OX2 6GG, UK
*
†Email address for correspondence: james.fannon@ul.ie
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the instability properties of dense granular flow in inclined plane and plane shear geometries as tests for the compressible inertial-dependent rheology. The model, which is a recent generalisation of the incompressible 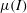$\unicode[STIX]{x1D707}(I)$ rheology, constitutes a hydrodynamical description of dense granular flow which allows for variability in the solids volume fraction. We perform a full linear stability analysis of the model and compare its predictions to existing experimental data for glass beads on an inclined plane and discrete element simulations of plane shear in the absence of gravity. In the case of the former, we demonstrate that the compressible model can quantitatively predict the instability properties observed experimentally, and, in particular, we find that it performs better than its incompressible counterpart. For the latter, the qualitative behaviour of the plane shear instability is also well captured by the compressible model.

JFM classification

Granular media: Granular media Waves/Free-surface Flows: Surface gravity waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 1026 - 1057
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M., Arakeri, V. H., Nott, P. R., Goddard, J. D. & Herrmann, H. J. 2005 Instability-induced ordering, universal unfolding and the role of gravity in granular Couette flow. J. Fluid Mech. 523, 277–306.Google Scholar
Alam, M. & Nott, P. R. 1997 The influence of friction on the stability of unbounded granular shear flow. J. Fluid Mech. 343, 267–301.Google Scholar
Alam, M. & Nott, P. R. 1998 Stability of plane Couette flow of a granular material. J. Fluid Mech. 377, 99–136.Google Scholar
Ancey, C. 2001 Dry granular flows down an inclined channel: experimental investigations on the frictional-collisional regime. Phys. Rev. E 65 (1), 011304.Google Scholar
Baker, J. L., Barker, T. & Gray, J. M. N. T. 2016a A two-dimensional depth-averaged rheology for dense granular avalanches. J. Fluid Mech. 787, 367–395.Google Scholar
Baker, J. L., Johnson, C. G. & Gray, J. M. N. T. 2016b Segregation-induced finger formation in granular free-surface flows. J. Fluid Mech. 809, 168–212.Google Scholar
Barker, T. & Gray, J. M. N. T. 2017 Partial regularisation of the incompressible 𝜇(I)-rheology for granular flow. J. Fluid Mech. 828, 5–32.Google Scholar
Barker, T., Schaeffer, D. G., Bohorquez, P. & Gray, J. M. N. T. 2015 Well-posed and ill-posed behaviour of the 𝜇(I) rheology for granular flow. J. Fluid Mech. 779, 794–818.Google Scholar
Barker, T., Schaeffer, D. G., Shearer, M. & Gray, J. M. N. T. 2017 Well-posed continuum equations for granular flow with compressibility and 𝜇(I)-rheology. Proc. R. Soc. Lond. A 473 (2201), 20160846.Google Scholar
Berzi, D. & Jenkins, J. T. 2015 Steady shearing flows of deformable, inelastic spheres. Soft Matt. 11, 4799–4808.Google Scholar
Bouzid, M., Trulsson, M., Claudin, P., Clément, E. & Andreotti, B. 2013 Nonlocal rheology of granular flows across yield conditions. Phys. Rev. Lett. 111, 238301.Google Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods. Dover Publications.Google Scholar
Brodu, N., Delannay, R., Valance, A. & Richard, P. 2015 New patterns in high-speed granular flows. J. Fluid Mech. 769, 218–228.Google Scholar
Chandrasekhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Dover Publications.Google Scholar
Da Cruz, F., Emam, S., Prochnow, M., Roux, J.-N. & Chevoir, F. 2005 Rheophysics of dense granular materials: discrete simulation of plane shear flows. Phys. Rev. E 72 (2), 021309.Google Scholar
Daerr, A. 2001 Dynamical equilibrium of avalanches on a rough plane. Phys. Fluids 13 (7), 2115–2124.Google Scholar
Delannay, R., Valance, A., Mangeney, A., Roche, O. & Richard, P. 2017 Granular and particle-laden flows: from laboratory experiments to field observations. J. Phys. D: Appl. Phys. 50 (5), 053001.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Edwards, A. N. & Gray, J. M. N. T. 2015 Erosion–deposition waves in shallow granular free-surface flows. J. Fluid Mech. 762, 35–67.Google Scholar
Fenistein, D. & van Hecke, M. 2003 Kinematics: wide shear zones in granular bulk flow. Nature 425 (6955), 256.Google Scholar
Forterre, Y. 2006 Kapiza waves as a test for three-dimensional granular flow rheology. J. Fluid Mech. 563, 123–132.Google Scholar
Forterre, Y. & Pouliquen, O. 2002 Stability analysis of rapid granular chute flows: formation of longitudinal vortices. J. Fluid Mech. 467, 361–387.Google Scholar
Forterre, Y. & Pouliquen, O. 2003 Long-surface-wave instability in dense granular flows. J. Fluid Mech. 486, 21–50.Google Scholar
Forterre, Y. & Pouliquen, O. 2008 Flows of dense granular media. Annu. Rev. Fluid Mech. 40, 1–24.Google Scholar
Fowler, A. 2011 Mathematical Geoscience. Springer Science & Business Media.Google Scholar
Fowler, A. C. 1997 Mathematical Models in the Applied Sciences. Cambridge University Press.Google Scholar
Goddard, J. D. & Lee, J. 2017 On the stability of the 𝜇(I) rheology for granular flow. J. Fluid Mech. 833, 302–331.Google Scholar
Goddard, J. D. & Lee, J. 2018 Regularization by compressibility of the 𝜇(I) model of dense granular flow. Phys. Fluids 30 (7), 073302.Google Scholar
Gray, J. M. N. T. 2001 Granular flow in partially filled slowly rotating drums. J. Fluid Mech. 441, 1–29.Google Scholar
Gray, J. M. N. T. & Edwards, A. N. 2014 A depth-averaged rheology for shallow granular free-surface flows. J. Fluid Mech. 755, 503–534.Google Scholar
Gray, J. M. N. T., Gajjar, P. & Kokelaar, P. 2015 Particle-size segregation in dense granular avalanches. C. R. Phys. 16 (1), 73–85.Google Scholar
Gray, J. M. N. T., Tai, Y.-C. & Noelle, S. 2003 Shock waves, dead zones and particle-free regions in rapid granular free-surface flows. J. Fluid Mech. 491, 161–181.Google Scholar
Henann, D. L. & Kamrin, K. 2013 A predictive, size-dependent continuum model for dense granular flows. Proc. Natl Acad. Sci. USA 110 (17), 6730–6735.Google Scholar
Henann, D. L. & Kamrin, K. 2016 A finite element implementation of the nonlocal granular rheology. Intl J. Numer. Meth. Engng 108 (4), 273–302.Google Scholar
Heyman, J., Delannay, R., Tabuteau, H. & Valance, A. 2017 Compressibility regularizes the 𝜇(I)-rheology for dense granular flows. J. Fluid Mech. 830, 553–568.Google Scholar
Higham, N. J.(Ed.) 2015 The Princeton Companion to Applied Mathematics. Princeton University Press.Google Scholar
Jackson, R. 1983 Some mathematical and physical aspects of continuum models for the motion of granular materials. In Theory of Dispersed Multiphase Flow (ed. Meyer, R. E.), pp. 291–337. Academic Press.Google Scholar
Jaeger, H. M., Nagel, S. R. & Behringer, R. P. 1996 Granular solids, liquids, and gases. Rev. Mod. Phys. 68 (4), 1259–1273.Google Scholar
Jenkins, J. T. & Savage, S. B. 1983 A theory for the rapid flow of identical, smooth, nearly elastic, spherical particles. J. Fluid Mech. 130, 187–202.Google Scholar
Jop, P. 2015 Rheological properties of dense granular flows. C. R. Phys. 16 (1), 62–72.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2005 Crucial role of sidewalls in granular surface flows: consequences for the rheology. J. Fluid Mech. 541, 167–192.Google Scholar
Jop, P., Forterre, Y. & Pouliquen, O. 2006 A constitutive law for dense granular flows. Nature 441 (7094), 727–730.Google Scholar
Kamrin, K. & Henann, D. L. 2015 Nonlocal modeling of granular flows down inclines. Soft Matt. 11 (1), 179–185.Google Scholar
Kamrin, K. & Koval, G. 2012 Nonlocal constitutive relation for steady granular flow. Phys. Rev. Lett. 108 (17), 178301.Google Scholar
Koval, G., Roux, J.-N., Corfdir, A. & Chevoir, F. 2009 Annular shear of cohesionless granular materials: from the inertial to quasistatic regime. Phys. Rev. E 79 (2), 021306.Google Scholar
Kumaran, V. & Maheshwari, S. 2012 Transition due to base roughness in a dense granular flow down an inclined plane. Phys. Fluids 24 (5), 053302.Google Scholar
Malik, M., Alam, M. & Dey, J. 2006 Nonmodal energy growth and optimal perturbations in compressible plane Couette flow. Phys. Fluids 18 (3), 034103.Google Scholar
Malik, M. R. 1990 Numerical methods for hypersonic boundary layer stability. J. Comput. Phys. 86 (2), 376–413.Google Scholar
Mandal, S. & Khakhar, D. V. 2016 A study of the rheology of planar granular flow of dumbbells using discrete element method simulations. Phys. Fluids 28 (10), 103301.Google Scholar
Midi, G. D. R. 2004 On dense granular flows. Eur. Phys. J. E 14 (4), 341–365.Google Scholar
Moyles, I. & Wetton, B. 2015 Fingering phenomena in immiscible displacement in porous media flow. J. Engng Maths 90 (1), 83–104.Google Scholar
Mueth, D. M., Debregeas, G. F., Karczmar, G. S., Eng, P. J., Nagel, S. R. & Jaeger, H. M. 2000 Signatures of granular microstructure in dense shear flows. Nature 406 (6794), 385–389.Google Scholar
Müller, S. B. & Kleiser, L. 2008 Viscous and inviscid spatial stability analysis of compressible swirling mixing layers. Phys. Fluids 20 (11), 114103.Google Scholar
Pihler-Puzović, D. & Mullin, T. 2013 The timescales of granular segregation in horizontally shaken monolayers. Proc. R. Soc. Lond. A 469 (2157), 20130203.Google Scholar
Pouliquen, O. 1999 Scaling laws in granular flows down rough inclined planes. Phys. Fluids 11 (3), 542–548.Google Scholar
Pouliquen, O., Cassar, C., Jop, P., Forterre, Y. & Nicolas, M. 2006 Flow of dense granular material: towards simple constitutive laws. J. Stat. Mech.-Theory E 2006 (07), P07020.Google Scholar
Pouliquen, O. & Forterre, Y. 2002 Friction law for dense granular flows: application to the motion of a mass down a rough inclined plane. J. Fluid Mech. 453, 133–151.Google Scholar
Pouliquen, O. & Forterre, Y. 2009 A non-local rheology for dense granular flows. Phil. Trans. R. Soc. Lond. A 367 (1909), 5091–5107.Google Scholar
Rao, K. K., Nott, P. R. & Sundaresan, S. 2008 An Introduction to Granular Flow. Cambridge University Press.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schofield, A. & Wroth, P. 1968 Critical State Soil Mechanics. McGraw-Hill.Google Scholar
Sun, J. & Sundaresan, S. 2011 A constitutive model with microstructure evolution for flow of rate-independent granular materials. J. Fluid Mech. 682, 590–616.Google Scholar
Tejchman, J. & Gudehus, G. 2001 Shearing of a narrow granular layer with polar quantities. Intl J. Numer. Anal. Meth. Geomech. 25 (1), 1–28.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. SIAM.Google Scholar
Trulsson, M., Andreotti, B. & Claudin, P. 2012 Transition from the viscous to inertial regime in dense suspensions. Phys. Rev. Lett. 109, 118305.Google Scholar
Trulsson, M., Bouzid, M., Claudin, P. & Andreotti, B. 2013 Dynamic compressibility of dense granular shear flows. Eur. Phys. Lett. 103 (3), 38002.Google Scholar
Varsakelis, C. & Papalexandris, M. V. 2016 Stability of wall bounded, shear flows of dense granular materials: the role of the Couette gap, the wall velocity and the initial concentration. J. Fluid Mech. 791, 384–413.Google Scholar
Viroulet, S., Baker, J. L., Rocha, F. M., Johnson, C. G., Kokelaar, B. P. & Gray, J. M. N. T. 2018 The kinematics of bidisperse granular roll waves. J. Fluid Mech. 848, 836–875.Google Scholar
Wang, C.-H., Jackson, R. & Sundaresan, S. 1996 Stability of bounded rapid shear flows of a granular material. J. Fluid Mech. 308, 31–62.Google Scholar
Woodhouse, M. J., Thornton, A. R., Johnson, C. G., Kokelaar, B. P. & Gray, J. M. N. T. 2012 Segregation-induced fingering instabilities in granular free-surface flows. J. Fluid Mech. 709, 543–580.Google Scholar
Supplementary material: File

Fannon et al. supplementary material

Fannon et al. supplementary material 1

Download Fannon et al. supplementary material(File)
File 157.4 KB