Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T12:28:45.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Drop impact on a solid surface: short-time self-similarity

Published online by Cambridge University Press:  13 April 2016

Julien Philippi ,
Pierre-Yves Lagrée  and
Arnaud Antkowiak
Julien Philippi
Affiliation:
Sorbonne Universités, UPMC Univ Paris 06, CNRS, UMR 7190 Institut Jean Le Rond d’Alembert, F-75005 Paris, France
Pierre-Yves Lagrée
Affiliation:
Sorbonne Universités, UPMC Univ Paris 06, CNRS, UMR 7190 Institut Jean Le Rond d’Alembert, F-75005 Paris, France
Arnaud Antkowiak*
Affiliation:
Sorbonne Universités, UPMC Univ Paris 06, CNRS, UMR 7190 Institut Jean Le Rond d’Alembert, F-75005 Paris, France
*
†Email address for correspondence: arnaud.antkowiak@upmc.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The early stages of drop impact onto a solid surface are considered. Detailed numerical simulations and detailed asymptotic analysis of the process reveal a self-similar structure both for the velocity field and the pressure field. The latter is shown to exhibit a maximum not near the impact point, but rather at the contact line. The motion of the contact line is furthermore shown to exhibit a ‘tank-treading’ motion. These observations are apprehended with the help of a variant of Wagner theory for liquid impact. This framework offers a simple analogy where the fluid motion within the impacting drop may be viewed as the flow induced by a flat rising expanding disk. The theoretical predictions are found to be in very close agreement both qualitatively and quantitatively with the numerical observations for approximately three decades in time. 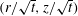Interestingly, the inviscid self-similar impact pressure and velocities are shown to depend solely on the self-similar variables $(r/\sqrt{t},z/\sqrt{t})$. The structure of the boundary layer developing along the wet substrate is investigated as well. It is found to be in first approximation analogous to the boundary layer growing in the trail of a shockwave. Interestingly, the corresponding boundary layer structure only depends on the impact self-similar variables. This allows us to construct a seamless uniform analytical approximation encompassing both impact and viscous effects. The depiction of the different dynamical fields enables to quantitatively predict observables of interest, such as the evolution of the integral viscous shearing force and of the net normal force.

JFM classification

Boundary Layers: Boundary layer structure Drops and Bubbles: Drops
Type
Papers
Information
Journal of Fluid Mechanics , Volume 795 , 25 May 2016 , pp. 96 - 135
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antkowiak, A., Audoly, B., Josserand, C., Neukirch, S. & Rivetti, M. 2011 Instant fabrication and selection of folded structures using drop impact. Proc. Natl Acad. Sci. USA 108 (26), 10400–10404.Google Scholar
Blake, T. D., Bracke, M. & Shikhmurzaev, Y. D. 1999 Experimental evidence of nonlocal hydrodynamic influence on the dynamic contact angle. Phys. Fluids 11 (8), 1995–2007.Google Scholar
Brown, D. L., Cortez, R. & Minion, M. L. 2001 Accurate projection methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 168 (2), 464–499.Google Scholar
Chen, Q., Ramé, E. & Garoff, S. 1997 The velocity field near moving contact lines. J. Fluid Mech. 337, 49–66.Google Scholar
Cointe, R. 1989 Two-dimensional water-solid impact. J. Offshore Mech. Arctic Engng 111 (2), 109–114.CrossRefGoogle Scholar
Cointe, R. & Armand, J. L. 1987 Hydrodynamic impact analysis of a cylinder. J. Offshore Mech. Arctic Engng 109 (3), 237–243.CrossRefGoogle Scholar
Darrozès, J.-S. & François, C. 1982 Mécanique Des Fluides Incompressibles, Lecture Notes in Physics. Springer-Verlag.Google Scholar
Duchemin, L. & Josserand, C. 2011 Curvature singularity and film-skating during drop impact. Phys. Fluids 23 (9), 091701.Google Scholar
Dussan, V., Elizabeth, B. & Davis, S. H. 1974 On the motion of a fluid–fluid interface along a solid surface. J. Fluid Mech. 65, 71–95.Google Scholar
Eggers, J., Fontelos, M. A., Josserand, C. & Zaleski, S. 2010 Drop dynamics after impact on a solid wall: Theory and simulations. Phys. Fluids 22 (6), 062101.Google Scholar
Elliott, J. W. & Smith, F. T. 2015 Ice formation on a smooth or rough cold surface due to the impact of a supercooled water droplet. J. Engng Maths 1–30.Google Scholar
Ellison, W. D. 1945 Some effects of raindrops and surface-flow on soil erosion and infiltration. EOS Trans. AGU 26 (3), 415–429.Google Scholar
Engel, O. G. 1955 Waterdrop collisions with solid surfaces. J. Res. Natl Bur. Stand. 54 (5), 281–298.Google Scholar
Howison, S. D., Ockendon, J. R., Oliver, J. M., Purvis, R. & Smith, F. T. 2005 Droplet impact on a thin fluid layer. J. Fluid Mech. 542 (-1), 1–23.Google Scholar
Howison, S. D., Ockendon, J. R. & Wilson, S. K. 1991 Incompressible water-entry problems at small deadrise angles. J. Fluid Mech. 222, 215–230.Google Scholar
Josserand, C., Ray, P. & Zaleski, S.2015 Droplet impact on a thin liquid film: anatomy of the splash. (in preparation).Google Scholar
Josserand, C. & Thoroddsen, S. T. 2016 Drop impact on a solid surface. Annu. Rev. Fluid Mech. 48 (1).Google Scholar
Josserand, C. & Zaleski, S. 2003 Droplet splashing on a thin liquid film. Phys. Fluids 15 (6), 1650–1657.Google Scholar
Korobkin, A. A. 2007 Second-order wagner theory of wave impact. J. Engng Maths 58 (1–4), 121–139.CrossRefGoogle Scholar
Lagrée, P.-Y. 2003 A triple deck model of ripple formation and evolution. Phys. Fluids 15 (8), 2355–2368.Google Scholar
Lagrée, P.-Y. 2010 Interactive boundary layers. In Asymptotic Methods in Fluid Mechanics: Survey and Recent Advances, CISM International Centre for Mechanical Sciences. Springer.Google Scholar
Lagrée, P.-Y., Staron, L. & Popinet, S. 2011 The granular column collapse as a continuum: validity of a two-dimensional Navier–Stokes model with a 𝜇(i)-rheology. J. Fluid Mech. 686, 378–408.Google Scholar
Lagubeau, G., Fontelos, M. A., Josserand, C., Maurel, A., Pagneux, V. & Petitjeans, P. 2012 Spreading dynamics of drop impacts. J. Fluid Mech. 713, 50–60.CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Lee, J. S., Weon, B. M., Je, J. H. & Fezzaa, K. 2012 How does an air film evolve into a bubble during drop impact? Phys. Rev. Lett. 109, 204501.Google Scholar
Leguédois, S., Planchon, O., Legout, C. & Le Bissonnais, Y. 2005 Splash projection distance for aggregated soils. Soil Sci. Soc. Am. J. 30–37.Google Scholar
Mangili, S., Antonini, C., Marengo, M. & Amirfazli, A. 2012 Understanding the drop impact phenomenon on soft pdms substrates. Soft Matt. 8, 10045–10054.Google Scholar
Mani, M., Mandre, S. & Brenner, M. P. 2010 Events before droplet splashing on a solid surface. J. Fluid Mech. 647 (-1), 163–185.Google Scholar
Mirels, H. 1955 laminar boundary layer behind shock advancing into stationary fluid. NACA TN 3401, 25.Google Scholar
Nethercote, W. C. E., Mackay, M. & Menon, B. C. 1986 Some Warship Slamming Investigations. Defence Research Establishment Atlantic.Google Scholar
Oliver, J. M.2002 Water entry and related problems. PhD thesis, University of Oxford.Google Scholar
Oliver, J. M. 2007 Second-order wagner theory for two-dimensional water-entry problems at small deadrise angles. J. Fluid Mech. 572, 59–86.Google Scholar
Pasandideh-Fard, M., Qiao, Y. M., Chandra, S. & Mostaghimi, J. 1996 Capillary effects during droplet impact on a solid surface. Phys. Fluids 8 (3), 650–659.Google Scholar
Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible euler equations in complex geometries. J. Comput. Phys. 190 (2), 572–600.Google Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228 (16), 5838–5866.Google Scholar
Pruppacher, H. R. & Beard, K. V. 1970 A wind tunnel investigation of the internal circulation and shape of water drops falling at terminal velocity in air. Q. J. R. Meteorol. Soc. 96 (408), 247–256.Google Scholar
Rein, M. 1993 Phenomena of liquid drop impact on solid and liquid surfaces. Fluid Dyn. Res. 12 (2), 61–93.Google Scholar
Renardy, Y., Popinet, S., Duchemin, L., Renardy, M., Zaleski, S., Josserand, C., Drumright-Clarke, M. A., Richard, D. & Quéré, D. 2003 Pyramidal and toroidal water drops after impact on a solid surface. J. Fluid Mech. 484, 69–83.Google Scholar
Reznik, S. N. & Yarin, A. L. 2002 Spreading of a viscous drop due to gravity and capillarity on a horizontal or an inclined dry wall. Phys. Fluids 14 (1), 118–132.Google Scholar
Riboux, G. & Gordillo, J. M. 2014 Experiments of drops impacting a smooth solid surface: A model of the critical impact speed for drop splashing. Phys. Rev. Lett. 113, 024507.Google Scholar
Richard, D. & Quéré, D. 2000 Bouncing water drops. Eur. Phys. Lett. 50 (6), 769–775.CrossRefGoogle Scholar
Rioboo, R., Marengo, M. & Tropea, C. 2002 Time evolution of liquid drop impact onto solid, dry surfaces. Exp. Fluids 33 (1), 112–124.Google Scholar
Schlichting, H. 1968 Boundary-layer Theory. McGraw-Hill.Google Scholar
Schmieden, C. 1953 Der Aufschlag von Rotationskörpern auf eine Wasseroberfläche. Richard v. Mises zum 70. Geburtstag gewidmet. Z. Angew. Math. Mech. 33 (4), 147–151.Google Scholar
Šikalo, Š., Wilhelm, H.-D., Roisman, I. V., Jakirlić, S. & Tropea, C. 2005 Dynamic contact angle of spreading droplets: Experiments and simulations. Phys. Fluids 17 (6).Google Scholar
Smith, F. T., Li, L. & Wu, G. X. 2003 Air cushioning with a lubrication/inviscid balance. J. Fluid Mech. 482, 291–318.Google Scholar
Sneddon, I. N. 1960 The elementary solution of dual integral equations. Glasgow Math. J. 4, 108–110.Google Scholar
Sneddon, I. N. 1995 Fourier Transforms. Dover.Google Scholar
Staron, L., Lagrée, P.-Y., Ray, P. & Popinet, S. 2013 Scaling laws for the slumping of a bingham plastic fluid. J. Rheol. 57 (4).Google Scholar
Stebnovskii, S. V. 1979 Characteristics in the initial stage of the spreading of a drop on a solid surface. J. Appl. Mech. Tech. Phys. 20 (1), 66–69.Google Scholar
Stewartson, K. 1964 The Theory of Laminar Boundary Layers in Compressible Fluids, Oxford Mathematical Monographs. Clarendon.CrossRefGoogle Scholar
Stow, C. D. & Hadfield, M. G. 1981 An experimental investigation of fluid flow resulting from the impact of a water drop with an unyielding dry surface. Proc. R. Soc. Lond. A 373 (1755), 419–441.Google Scholar
Stow, C. D. & Stainer, R. D. 1977 The physical products of a splashing water drop. J. Met. Soc. Japan. II 55 (5), 518–532.CrossRefGoogle Scholar
Thoroddsen, S. T., Etoh, T. G., Takehara, K., Ootsuka, N. & Hatsuki, Y. 2005 The air bubble entrapped under a drop impacting on a solid surface. J. Fluid Mech. 545, 203–212.Google Scholar
Van Dyke, M. D. 1975 Perturbation Methods in Fluid Dynamics. Parabolic Press.Google Scholar
Villermaux, E. & Bossa, B. 2011 Drop fragmentation on impact. J. Fluid Mech. 668, 412–435.Google Scholar
Wagner, H. 1932 Über stoß- und gleitvorgänge an der oberfläche von flüssigkeiten. Z. Angew. Math. Mech. 12 (4), 193–215.Google Scholar
Weiss, D. A. & Yarin, A. L. 1999 Single drop impact onto liquid films: neck distortion, jetting, tiny bubble entrainment, and crown formation. J. Fluid Mech. 385, 229–254.Google Scholar
Xu, L., Zhang, W. W. & Nagel, S. R. 2005 Drop splashing on a dry smooth surface. Phys. Rev. Lett. 94 (18), 184505–4.Google Scholar
Yarin, A. L. & Weiss, D. A. 1995 Impact of drops on solid surfaces: self-similar capillary waves, and splashing as a new type of kinematic discontinuity. J. Fluid Mech. 283, 141–173.Google Scholar