Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-16T04:09:49.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Formation of drops and rings in double-diffusive sedimentation

Published online by Cambridge University Press:  17 December 2019

Yi-Ju Chou Open the ORCID record for Yi-Ju Chou [Opens in a new window] ,
Chen-Yen Hung  and
Chien-Fu Chen Open the ORCID record for Chien-Fu Chen [Opens in a new window]
Yi-Ju Chou*
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei106, Taiwan Center for Advanced Study in Theoretical Sciences, National Taiwan University, Taipei106, Taiwan
Chen-Yen Hung
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei106, Taiwan
Chien-Fu Chen
Affiliation:
Institute of Applied Mechanics, National Taiwan University, Taipei106, Taiwan
*
†Email address for correspondence: yjchou@iam.ntu.edu.tw
Get access Rights & Permissions [Opens in a new window]

Abstract

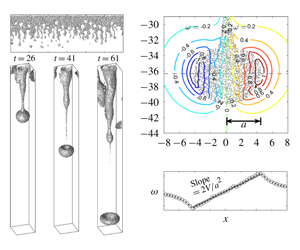
We conduct numerical simulations to investigate the formation and evolution of drops and vortex rings of particle-laden fingers in double-diffusive convection in stably stratified environments. We show that the temporal evolution can be divided into double diffusion, acceleration and deceleration phases. The acceleration phase is a result of the vanishing temperature perturbation in the drop during the descent in the layer of uniform temperature. The drop decelerates because it transforms into a vortex ring. A theoretical drag model is presented to predict the speed of the spherical drop with the low drop Reynolds number. By formulating the boundary condition based on the vorticity, our drag model gives a more general form of the drag coefficient for small spherical drops and shows good agreement in predicting the drag coefficient. Drops with five particle sizes are compared, and it is found that although the greater vertical settling enhances vertical transport, the final state differs little among the various sizes. Comparison of our drag model with the simulation results under various bulk conditions and previous experimental results shows good model predictability. Finally, a comparison with the salt-finger case shows that the diffusive nature of the dissolved scalar field, along with the wake effect, can result in an apparent loss of mass from the drop and a permanent presence of the connection between the drop and its parent finger. This makes the observed detachment of the particle-laden drop much less likely in the salt-finger case.

JFM classification

Convection: Double diffusive convection Geophysical and Geological Flows: Sediment transport Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A35
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alldredge, A. & Cohen, Y. 1987 Can microscale chemical patches persist in the sea? Microelectrode study of marine snow, fecal pellets. Science 235, 689–691.CrossRefGoogle ScholarPubMed
Arthur, R. S. & Fringer, O. B. 2014 The dynamics of breaking internal solitary waves on slopes. J. Fluid Mech. 761, 360–398.CrossRefGoogle Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.CrossRefGoogle Scholar
Boussinesq, J. 1913 Existence of a superficial viscosity in the thin transition layer separating one liquid from another contiguous fluid. C. R. Acad. Sci. USA 156, 983–989.Google Scholar
Burns, P. & Meiburg, E. 2012 Sediment-laden fresh water above salt water: linear stability analysis. J. Fluid Mech. 691, 279–314.CrossRefGoogle Scholar
Burns, P. & Meiburg, E. 2015 Sediment-laden fresh water above salt water: nonlinear simulations. J. Fluid Mech. 762, 156–195.CrossRefGoogle Scholar
Bush, J. W., Thurber, B. A. & Blanchette, F. 2003 Particle clouds in homogeneous and stratified environments. J. Fluid Mech. 489, 29–54.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon Press.Google Scholar
Chang, Y.-C., Chiu, T.-Y., Hung, Y.-C. & Chou, Y.-J. 2019 Three-dimensional Eulerian–Lagrangian simulation of particle settling in inclined water columns. Powder Technol. 348, 80–92.CrossRefGoogle Scholar
Chen, C. F. 1997 Particle flux through sediment fingers. Deep-Sea Res. I 44 (9–10), 1645–1654.CrossRefGoogle Scholar
Chester, W., Breach, D. R. & Proudman, I. 1969 On the flow past a sphere at low Reynolds number. J. Fluid Mech. 37, 751–760.CrossRefGoogle Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Math. Comput. 22, 133–147.CrossRefGoogle Scholar
Chou, Y.-J., Cheng, C.-J., Chen, R.-L. & Hung, C.-Y. 2019 Instabilities of particle-laden layers in the stably stratified environment. Phys. Fluids doi:10.1063/1.5123317.Google Scholar
Chou, Y. J. & Fringer, O. B. 2008 Modeling dilute sediment suspension using large-eddy simulation with a dynamic mixed model. Phys. Fluids 20, 11503.CrossRefGoogle Scholar
Chou, Y. J. & Fringer, O. B. 2010 A model for the simulation of coupled flow-bedform evolution in turbulent flows. J. Geophys. Res. 115, C10041.CrossRefGoogle Scholar
Chou, Y.-J., Gu, S.-H. & Shao, Y.-C. 2015 An Euler–Lagrange model for simulating fine particle suspension in liquid flows. J. Comput. Phys. 299, 955–973.CrossRefGoogle Scholar
Chou, Y.-J. & Shao, Y.-C. 2016 Numerical study of particle-induced Rayleigh–Taylor instability: effect of particle settling and entrainment. Phys. Fluids 28, 043302.CrossRefGoogle Scholar
Chou, Y.-J., Wu, F.-C. & Shih, W.-R. 2014a Toward numerical modeling of fine particle suspension using a two-way coupled Euler–Euler model. Part 1. Theoretical formulation and implications. Intl J. Multiphase Flow 64, 35–43.CrossRefGoogle Scholar
Chou, Y.-J., Wu, F.-C. & Shih, W.-R. 2014b Toward numerical modeling of fine particle suspension using a two-way coupled Euler–Euler model. Part 2. Simulation of particle-induced Rayleigh–Taylor instability. Intl J. Multiphase Flow 64, 44–54.CrossRefGoogle Scholar
Cui, A. & Street, R. L. 2004 Large-eddy simulation of coastal upwelling flow. Environ. Fluid Mech. 4, 197–223.CrossRefGoogle Scholar
Cundall, R. & Strack, O. 1979 A discrete numerical model for granular assemblies. Geotechnique 29, 47–65.CrossRefGoogle Scholar
Elghobashi, S. & Truesdell, G. C. 1993 On the two-way interaction between homogeneous turbulence and dispersed solid particles. I. Turbulence modification. Phys. Fluids 5 (7), 1790.CrossRefGoogle Scholar
Ferry, J. & Balachandar, S. 2001 A fast Eulerian method for disperse two-phase flow. Intl J. Multiphase Flow 27, 1199–1226.CrossRefGoogle Scholar
Fringer, O. B. & Street, R. L. 2003 The dynamics of breaking progressive interfacial waves. J. Fluid Mech. 494, 319–353.CrossRefGoogle Scholar
Green, T. 1987 The importance of double diffusion to the settling of suspended material. Sedimentology 34, 319–331.CrossRefGoogle Scholar
Green, T. & Schettle, J. W. 1986 Vortex rings associated with strong double-diffusive fingering. Phys. Fluids 29 (7), 2109–2112.CrossRefGoogle Scholar
Hadamard, J. 1911 Slow permanent movement of a viscous liquid sphere in a viscous liquid. C. R. Acad. Sci. 152, 1735–1738.Google Scholar
Hamdhan, I. N. & Clarke, B. G. 2010 Determination of thermal conductivity of coarse and fine sand soils. In Proceedings World Geothermal Congress, Bali, Indonesia, pp. 1–7. International Geothermal Association.Google Scholar
Hill, M. J. M. 1894 On a spherical vortex. Phil. Trans. R. Soc. Lond. A 185, 213–245.CrossRefGoogle Scholar
Hizzett, J. L., Hughes Clarke, J. E., Sumner, E. J., Cartigny, M. J. B., Talling, P. J. & Clare, M. A. 2018 Which triggers produce the most erosive, frequent, and longest runout turbidity currents on deltas? Geophys. Res. Lett. 45, 855–863.CrossRefGoogle Scholar
Houk, D. & Green, T. 1973 Descent rates of suspension fingers. Deep-Sea Res. 20, 757–761.Google Scholar
Hoyal, D. C., Bursik, M. I. & Atkinson, J. F. 1999 The influence of diffusive convection on sedimentation from buoyant plumes. Mar. Geol. 159, 205–220.CrossRefGoogle Scholar
Huppert, H. E. & Turner, J. S. 1981 Double-diffusive convection. J. Fluid Mech. 106, 299–329.CrossRefGoogle Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Leonard, B. P. 1979 A stable and accurate convective modelling procedure based on quadratic upstream interpolation. Comput. Meth. Appl. Mech. Engng 19, 59–98.CrossRefGoogle Scholar
Linden, P. F. 1973 On the structure of salt fingers. Deep-Sea Res. 20, 325–340.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion of a small sphere in linear shear flows. Phys. Fluids 26, 883–889.CrossRefGoogle Scholar
Moffatt, H. K. & Moore, D. W. 1978 The response of Hill’s spherical vortex to a small axisymmetric disturbance. J. Fluid Mech. 87 (4), 749–760.CrossRefGoogle Scholar
Parsons, J. D., Bush, J. W. M. & Syvitski, J. P. M. 2001 Hyperpycnal plume formation from riverine outflows with small sediment concentrations. Sedimentology 48, 465–478.CrossRefGoogle Scholar
Parsons, J. D. & Garcia, M. H. 2000 Enhanced sediment scavenging due to double-diffusive convection. J. Sedim. Res. 70, 47–52.CrossRefGoogle Scholar
Perng, C. Y. & Street, R. L. 1989 Three-dimensional unsteady flow simulations: alternative strategies for a volume-average calculation. Intl J. Numer. Fluids 9 (3), 341–362.CrossRefGoogle Scholar
Pozrikidis, C. 1986 The nonlinear instability of Hill’s vortex. J. Fluid Mech. 168, 337–367.CrossRefGoogle Scholar
Proudman, I. & Pearson, J. R. A. 1957 Expansion at small Reynolds numbers for the flow past a sphere and a circular cylinder. J. Fluid Mech. 2, 237–262.CrossRefGoogle Scholar
Radko, T. 2013 Double-Diffusive Convection. Cambridge University Press.CrossRefGoogle Scholar
Reali, J. F., Garaud, P., Alsinan, A. & Meiburg, E. 2018 Layer formation in sedimentary fingering convection. J. Fluid Mech. 816, 268–305.CrossRefGoogle Scholar
Rybczynski, W. 1911 On the translatory motion of a fluid sphere in a viscous medium. Bull. Acad. Sci. Cracow Ser. A 2, 40.Google Scholar
Schiller, L. & Nauman, A. 1935 A drag coefficient correlation. VDI Zeitung 77, 318–320.Google Scholar
Schmitt, R. W. 1979 Flux measurements on salt fingers at in interface. J. Mar. Res. 37, 419–436.Google Scholar
Schmitt, R. W. 1994 Double-diffusion in oceanography. Annu. Rev. Fluid Mech. 26, 255–285.CrossRefGoogle Scholar
Schmitt, R. W. & Evane, D. L. 1978 An estimate of the vertical mixing due to salt fingers based on observations in the North Atlantic central water. J. Geophys. Res. 83, 2913–2919.CrossRefGoogle Scholar
Schmitt, R. W., Ledwell, J. R., Montgomery, E. T., Polzin, K. L. & Toole, J. M. 2005 Enhanced diapycnal mixing by salt fingers in the thermocline of the tropical atlantic. Science 308, 685–688.CrossRefGoogle ScholarPubMed
Segre, P. N., Liu, F., Umbanhowar, P. & Weitz, D. A. 2001 An effective gravitational temperature for sedimentation. Nature 409, 594–597.CrossRefGoogle ScholarPubMed
Shao, Y.-C., Hung, C.-Y. & Chou, Y.-J. 2017 Numerical study of convective sedimentation through a sharp density interface. J. Fluid Mech. 824, 513–549.CrossRefGoogle Scholar
Taylor, J. R. & Bucens, P. 1989 Laboratory experiments on the structure of salt fingers. Deep-Sea Res. A 36, 1675–1704.CrossRefGoogle Scholar
Turner, J. S. 1957 Buoyant vortex rings. Proc. R. Soc. Lond. A 239, 61–75.Google Scholar
Turner, J. S. 1967 Salt fingers across a density interface. Deep-Sea Res. 14, 599–611.Google Scholar
Venayagamoorthy, S. K. & Fringer, O. B. 2007 On the formation and propagation of nonlinear internal boluses across a shelf break. J. Fluid Mech. 577, 137–159.CrossRefGoogle Scholar
Wang, R.-Q., Law, A. W.-K., Adams, E. E. & Fringer, O. B. 2009 Buoyant formation number of a starting buoyant jet. Phys. Fluids 21 (12), 125104.CrossRefGoogle Scholar
Yu, X., Hsu, T.-J. & Balachandar, S. 2013 Convective instability in sedimentation: linear stability analysis. J. Geophys. Res. 118, 256–272.CrossRefGoogle Scholar
Yu, X., Hsu, T.-J. & Balachandar, S. 2014 Convective instability in sedimentation: 3-D numerical study. J. Geophys. Res. 119, 8141–8161.CrossRefGoogle Scholar
Zang, Y. & Street, R. L. 1995 Numerical simulation of coastal upwelling and interfacial instability of a rotational and stratified fluid. J. Fluid Mech. 305, 47–75.CrossRefGoogle Scholar
Zang, Y., Street, R. L. & Koseff, J. R. 1994 A non-staggered grid, fractional step method for time-dependent incompressible Navier–Stokes equations in curvilinear coordinates. J. Comput. Phys. 114, 18–33.CrossRefGoogle Scholar
Zedler, E. A. & Street, R. L. 2001 Large-eddy simulation of sediment transport: current over ripples. J. Hydraul. Engng. 127 (6), 444–452.CrossRefGoogle Scholar
Zedler, E. A. & Street, R. L. 2006 Sediment transport over ripples in oscillatory flow. J. Hydraul. Engng. 132 (2), 180–193.CrossRefGoogle Scholar
Zhao, W., Frankel, S. F. & Mongeau, L. G. 2000 Effects of trailing jet instability on vortex ring formation. Phys. Fluids 12 (3), 589–596.CrossRefGoogle Scholar