Published online by Cambridge University Press: 10 March 2014
We study geostrophic adjustment in rotating barotropic fluid when the angular speed of rotation  $\boldsymbol{\Omega}$ does not coincide in direction with the acceleration due to gravity; the traditional and hydrostatic approximations are not used. Linear adjustment results in a tendency of any localized initial state towards a geostrophically balanced steady columnar motion with columns parallel to
$\boldsymbol{\Omega}$ does not coincide in direction with the acceleration due to gravity; the traditional and hydrostatic approximations are not used. Linear adjustment results in a tendency of any localized initial state towards a geostrophically balanced steady columnar motion with columns parallel to 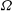 $\boldsymbol{\Omega}$. Nonlinear adjustment is examined for small Rossby numbers Ro and aspect ratio
$\boldsymbol{\Omega}$. Nonlinear adjustment is examined for small Rossby numbers Ro and aspect ratio 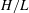 $H/L$ (
$H/L$ (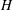 $H$ and
$H$ and 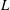 $L$ are the layer depth and the horizontal scale of motion), using multiple-time-scale perturbation theory. It is shown that an arbitrary perturbation is split in a unique way into slow and fast components evolving with characteristic time scales
$L$ are the layer depth and the horizontal scale of motion), using multiple-time-scale perturbation theory. It is shown that an arbitrary perturbation is split in a unique way into slow and fast components evolving with characteristic time scales 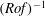 $(\mathit{Ro}f)^{-1}$ and
$(\mathit{Ro}f)^{-1}$ and 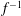 $f^{-1}$, respectively, where
$f^{-1}$, respectively, where 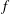 $f $ is the Coriolis parameter. The slow component does not depend on depth and is close to geostrophic balance. On times
$f $ is the Coriolis parameter. The slow component does not depend on depth and is close to geostrophic balance. On times 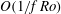 $O(1/f\, \mathit{Ro})$ the slow component is not influenced by the fast one and is described by the two-dimensional fluid dynamics equation for the geostrophic streamfunction. The fast component consists of long gyroscopic waves and is a packet of inertial oscillations modulated by an amplitude depending on coordinates and slow time. On times
$O(1/f\, \mathit{Ro})$ the slow component is not influenced by the fast one and is described by the two-dimensional fluid dynamics equation for the geostrophic streamfunction. The fast component consists of long gyroscopic waves and is a packet of inertial oscillations modulated by an amplitude depending on coordinates and slow time. On times 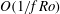 $O(1/f\, \mathit{Ro})$ the fast component conserves its energy, but it is coupled to the slow component: its amplitude obeys an equation with coefficients depending on the geostrophic streamfunction. Under the traditional approximation, the inertial oscillations are trapped by the quasi-geostrophic component; ‘non-traditional’ terms in the amplitude equation provide a meridional dispersion of the packet on times
$O(1/f\, \mathit{Ro})$ the fast component conserves its energy, but it is coupled to the slow component: its amplitude obeys an equation with coefficients depending on the geostrophic streamfunction. Under the traditional approximation, the inertial oscillations are trapped by the quasi-geostrophic component; ‘non-traditional’ terms in the amplitude equation provide a meridional dispersion of the packet on times 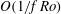 $O(1/f\, \mathit{Ro})$, and, therefore, an effective radiation of energy from the initial perturbation domain. Another important effect of the non-traditional terms is that on longer times
$O(1/f\, \mathit{Ro})$, and, therefore, an effective radiation of energy from the initial perturbation domain. Another important effect of the non-traditional terms is that on longer times 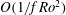 $O(1/f\, \mathit{Ro}^{2})$ a transfer of energy between the fast and the slow components becomes possible.
$O(1/f\, \mathit{Ro}^{2})$ a transfer of energy between the fast and the slow components becomes possible.