Hostname: page-component-77c89778f8-7drxs Total loading time: 0 Render date: 2024-07-18T09:38:15.074Z Has data issue: false hasContentIssue false
  • English
  • Français

Group scattering of point vortices on an unbounded plane

Published online by Cambridge University Press:  26 January 2021

V.G. Makarov Open the ORCID record for V.G. Makarov [Opens in a new window]
V.G. Makarov*
Affiliation:
Instituto Politécnico Nacional, Centro Interdisciplinario de Ciencias Marinas, La Paz, Baja California Sur23096, Mexico
*
†Email address for correspondence: smakarov@ipn.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

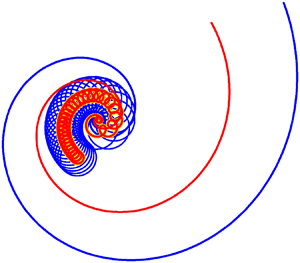
Group scattering of an initially compact two-dimensional configuration of N point vortices with strengths of different signs in an unbounded ideal fluid is investigated. This phenomenon manifests itself in a permanent increase of the vortex cloud, accompanied by mixing, clustering and emission of vortices. Possible mechanisms for such an evolution are considered, and the necessary condition is formulated. An invariant function of relative motion, F, is introduced, which is a combination of the first integrals of the system and can be expressed through 2(N−2) independent phase variables. We use this function to construct vortex equilibria and to investigate their nonlinear stability. Cases of N = 3 and N = 5 (for vortex configurations which possess central symmetry), when F depends on two variables only, are examined in detail. In addition to the familiar self-similar scattering (or collapse), we found a regime of asymptotically self-similar scattering (but not collapse) which occurs from any trajectory inside a certain finite domain in the phase space. A similar domain exists also for the case of dipole emission. A periodic absolute motion consisting of alternating stages of expansion and convergence of vortices is discussed. These mechanisms also work during group scattering. Simple examples of this phenomenon are given for the case of five vortices. Finally, group scattering is demonstrated for an initially compact cloud of 1009 vortices with strengths randomly distributed in the range (−1, 1). The area of the main part of the vortex cloud grows with time according to an almost linear law characteristic of self-similar motion.

JFM classification

Instability: Nonlinear instability Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 911 , 25 March 2021 , A24
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aref, H. 1979 Motion of three vortices. Phys. Fluids 22 (3), 393–400.CrossRefGoogle Scholar
Aref, H. 2007 Point vortex dynamics: a classical mathematics playground. J. Maths Phys. 48, 065401.CrossRefGoogle Scholar
Aref, H. 2009 Stability of relative equilibria of three vortices. Phys. Fluids 21, 094101.CrossRefGoogle Scholar
Aref, H. 2010 Self-similar motion of three point vortices. Phys. Fluids 22, 057104.CrossRefGoogle Scholar
Aref, H., Kadtke, J.B., Zawadzki, I., Campbell, L.J. & Eckhardt, B. 1988 Point vortex dynamics: recent results and open problems. Fluid Dyn. Res. 3, 63–74.CrossRefGoogle Scholar
Aref, H., Newton, P.K., Stremler, M.A., Tokieda, T. & Vainchtein, D.L. 2003 Vortex crystals. Adv. Appl. Mech. 39, 1–79.CrossRefGoogle Scholar
Aref, H., Rott, N. & Thomann, H. 1992 Gröbli's solution of the three-vortex problem. Annu. Rev. Fluid Mech. 24, 1–20.CrossRefGoogle Scholar
Aref, H. & Stremler, M.A. 1999 Four-vortex motion with zero total circulation and impulse. Phys. Fluids 11 (12), 3704–3715.CrossRefGoogle Scholar
Aref, H. & Vainchtein, D.L. 1998 Asymmetric equilibrium patterns of point vortices. Nature 392, 769–770.CrossRefGoogle Scholar
Bell, E.T. 1938 The iterated exponential integers. Ann. Maths 39 (3), 539–557.CrossRefGoogle Scholar
Borisov, A.V. & Lebedev, V.G. 1998 Dynamics of three vortices on a plane and a sphere – III. Noncompact case. Problems of collapse and scattering. Regular Chaotic Dyn. 3 (4), 74–86.CrossRefGoogle Scholar
Borisov, A.V. & Mamaev, I.S. 2005 Mathematical Methods in the Dynamics of Vortex Structures. R&C Dynamics, Institute of Computer Science (in Russian).Google Scholar
Chen, Y., Kolokolnikov, T. & Zhirov, D. 2013 Collective behavior of large number of vortices in the plane. Proc. R. Soc. A 469, 20130085.CrossRefGoogle Scholar
Demina, M.V. & Kudryashov, N.A. 2014 Rotation, collapse, and scattering of point vortices. Theor. Comput. Fluid Dyn. 28, 357–368.CrossRefGoogle Scholar
Eckhardt, B. 1988 Integrable four vortex motion. Phys. Fluids 31 (10), 2796–2801.CrossRefGoogle Scholar
Gröbli, W. 1877 Speziele Probleme über die Bewegung geradliniger paralleler Wirbelfäden. Vierteljahrschr. Naturforsch. Ges. Zürich 22, 37–81; 129–165.Google Scholar
Hampton, M., Roberts, G.E. & Santoprete, M. 2014 Relative equilibria in the four-vortex problem with two pairs of equal vorticities. J. Nonlinear Sci. 24, 39–92.CrossRefGoogle Scholar
Kimura, Y. 1990 Parametric motion of complex-time singularity toward real collapse. Physica D 46, 439–448.CrossRefGoogle Scholar
Kizner, Z. 2006 Stability and transitions of hetonic quartets and baroclinic modons. Phys. Fluids 18, 056601.CrossRefGoogle Scholar
Kizner, Z. 2011 Stability of point-vortex multipoles revisited. Phys. Fluids 23, 064104.CrossRefGoogle Scholar
Kizner, Z. 2014 On the stability of two-layer geostrophic point-vortex multipoles. Phys. Fluids 26, 046602.CrossRefGoogle Scholar
Kizner, Z., Khvoles, R. & Kessler, D.A. 2010 Viscous selection of an elliptical dipole. J. Fluid Mech. 658, 492–508.CrossRefGoogle Scholar
Kizner, Z., Shteinbuch-Fridman, B., Makarov, V. & Rabinovich, M. 2017 Cycloidal meandering of a mesoscale anticyclonic eddy. Phys. Fluids 29, 086601.CrossRefGoogle Scholar
Kravtsov, S. & Reznik, G. 2019 Numerical solutions of the singular vortex problem. Phys. Fluids 31, 066602.CrossRefGoogle Scholar
Kudela, H. 2014 Collapse of n-point vortices in self-similar motion. Fluid Dyn. Res. 46, 031414.CrossRefGoogle Scholar
Kurakin, L.G., Ostrovskaya, I.V. & Sokolovskiy, M.A. 2016 On the stability of discete tripole, quadropole, Thomson’ vortex triangle and square in a two-layer/homogeneous rotating fluid. Regular Chaotic Dyn. 21 (3), 291–334.CrossRefGoogle Scholar
Leoncini, X., Kuznetsov, L. & Zaslavsky, G.M. 2000 Motion of three vortices near collapse. Phys. Fluids 12 (8), 1911–1927.CrossRefGoogle Scholar
Leoncini, X., Kuznetsov, L. & Zaslavsky, G.M. 2001 Chaotic advection near a three-vortex collapse. Phys. Rev. E 63, 036224.CrossRefGoogle Scholar
Newton, P.K. 2001 The N-Vortex Problem: Analytical Techniques. Springer-Verlag.CrossRefGoogle Scholar
Newton, P.K. 2014 Point vortex dynamics in the post-Aref era. Fluid Dyn. Res. 46, 031401.CrossRefGoogle Scholar
Novikov, E.A. 1975 Dynamics and statistics of a system of vortices. Sov. Phys.-JETP 41 (5), 937–943.Google Scholar
Novikov, E.A. & Sedov, Y.B. 1979 Vortex collapse. Sov. Phys.-JETP 50 (2), 297–30l.Google Scholar
Press, W.H., Teukolsky, S.A., Vetterling, W.T. & Flannery, B.P. 1996 Numerical Recipes in Fortran 77: The Art of Scientific Computing, 2nd edn. Cambridge University Press.Google Scholar
Reznik, G.M. 1992 Dynamics of singular vortices on a β-plane. J. Fluid Mech. 240, 405–432.CrossRefGoogle Scholar
Reznik, G. & Kizner, Z. 2007 a Two-layer quasigeostrophic singular vortices embedded in a regular flow. Part I: invariants of motion and stability of vortex pairs. J. Fluid Mech. 584, 185–202.CrossRefGoogle Scholar
Reznik, G. & Kizner, Z. 2007 b Two-layer quasigeostrophic singular vortices embedded in a regular flow. Part II: Steady and unsteady drift of individual vortices on a beta-plane. J. Fluid Mech. 584, 203–223.CrossRefGoogle Scholar
Reznik, G. & Kizner, Z. 2010 Singular vortices in regular flows. Theor. Comput. Fluid Dyn. 24, 65–75.CrossRefGoogle Scholar
Roberts, G.E. 2013 Stability of relative equilibria in the planar n-vortex problem. SIAM J. Appl. Dyn. Syst. 12 (2), 1114–1134.CrossRefGoogle Scholar
Rott, N. 1990 Constrained three- and four-vortex problems. Phys. Fluids A 2 (8), 1477–1480.CrossRefGoogle Scholar
Sokolovskiy, M.A. & Verron, J. 2014 Dynamics of Vortex Structures in a Stratified Rotating Fluid. Series Atmospheric and Oceanographic Sciences Library, vol. 47. Springer.CrossRefGoogle Scholar
Synge, J.L. 1949 On the motion of three vortices. Can. J. Maths 1, 257–270.CrossRefGoogle Scholar
Tavantzis, J. & Ting, L. 1988 The dynamics of three vortices revisited. Phys. Fluids 31, 1392–1409.CrossRefGoogle Scholar
Trieling, R.R., van Heijst, G.J.F. & Kizner, Z. 2010 Laboratory experiments on multipolar vortices in a rotating fluid. Phys. Fluids 22, 094104.CrossRefGoogle Scholar