Hostname: page-component-84b7d79bbc-dwq4g Total loading time: 0 Render date: 2024-07-26T06:07:58.805Z Has data issue: false hasContentIssue false
  • English
  • Français

The high-Reynolds-number asymptotic development of nonlinear equilibrium states in plane Couette flow

Published online by Cambridge University Press:  30 May 2014

Kengo Deguchi  and
Philip Hall
Kengo Deguchi
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
Philip Hall*
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
*
†Email address for correspondence: philhall@ic.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

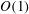The relationship between nonlinear equilibrium solutions of the full Navier–Stokes equations and the high-Reynolds-number asymptotic vortex–wave interaction (VWI) theory developed for general shear flows by Hall & Smith (J. Fluid Mech., vol. 227, 1991, pp. 641–666) is investigated. Using plane Couette flow as a prototype shear flow, we show that all solutions having $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}O(1)$ wavenumbers converge to VWI states with increasing Reynolds number. The converged results here uncover an upper branch of VWI solutions missing from the calculations of Hall & Sherwin (J. Fluid Mech., vol. 661, 2010, pp. 178–205). For small values of the streamwise wavenumber, the converged lower-branch solutions take on the long-wavelength state of Deguchi, Hall & Walton (J. Fluid Mech., vol. 721, 2013, pp. 58–85) while the upper-branch solutions are found to be quite distinct, with new states associated with instabilities of jet-like structures playing the dominant role. Between these long-wavelength states, a complex ‘snaking’ behaviour of solution branches is observed. The snaking behaviour leads to complex ‘entangled’ states involving the long-wavelength states and the VWI states. The entangled states exhibit different-scale fluid motions typical of those found in shear flows.

JFM classification

Mathematical Foundations: General fluid mechanics Mathematical Foundations: Mathematical Foundations Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 750 , 10 July 2014 , pp. 99 - 112
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, M., Mellibovsky, F., Roland, N. & Hof, B. 2013 Streamwise-localized solutions at the onset of turbulence in pipe flow. Phys. Rev. Lett. 110, 224502.Google Scholar
Blackburn, H. M., Hall, P. & Sherwin, S. J. 2013 Lower branch equilibria in Couette flow: the emergence of canonical states for arbitrary shear flows. J. Fluid Mech. 721, 58–85.Google Scholar
Deguchi, K., Hall, P. & Walton, A. G. 2013 The emergence of localized vortex–wave interaction states in plane Couette flow. J. Fluid Mech. 721, 58–85.Google Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2009 Localized edge states in plane Couette flow. Phys. Fluids 21, 111701.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hall, P. & Smith, F. T. 1989 Nonlinear Tollmien–Schlichting/vortex interaction in boundary layers. Eur. J. Mech. (B/Fluids) 8 (3), 179–205.Google Scholar
Hall, P. & Smith, F. T. 1990 Near-planar TS waves and longitudinal vortices in channel flow: nonlinear interaction and focussing. In Instability and Transition, pp. 5–39. Springer.Google Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.Google Scholar
Isoni, A.2014 Vortex wave interaction theory to understand self-sustaining processes in transitional flows. PhD thesis, Department of Aeronautics, Imperial College London, UK.Google Scholar
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. Japan 70, 703–716.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Kreilos, T. & Eckhardt, B. 2012 Periodic orbits near onset of chaos in plane Couette flow. Chaos 22, 047505.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.CrossRefGoogle Scholar
Schneider, T. M., Gibson, J. F. & Burke, J. 2010 Snakes and ladders: localized solutions of plane Couette flow. Phys. Rev. Lett. 104, 104501.Google Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96, 174101.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517–1534.Google Scholar
Wang, J., Gibson, J. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98, 204501.Google Scholar