Hostname: page-component-7479d7b7d-rvbq7 Total loading time: 0 Render date: 2024-07-13T00:21:49.991Z Has data issue: false hasContentIssue false
  • English
  • Français

The initial transient and approach to self-similarity of a very viscous buoyant thermal

Published online by Cambridge University Press:  12 March 2014

Gunnar G. Peng  and
John R. Lister
Gunnar G. Peng*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
John R. Lister
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: G.G.Peng@damtp.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

An isolated buoyant thermal in very viscous fluid has been shown to attain a self-similar form at large times which grows as 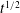$t^{1/2}$ (Whittaker & Lister J. Fluid Mech., vol. 606, 2008, pp. 295–324). For large values of the Rayleigh number 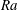$\mathit{Ra}$ (based on the conserved total buoyancy), the similarity solution is slender with a roughly spherical head at the top and a long tail that contains most of the buoyancy and extends down to the origin. We investigate the time-dependent behaviour of the thermal numerically; both the long-time behaviour in terms of perturbations to the similarity solution and the short-time evolution from a spherical initial condition. Using a spectral method, we find the growth rates of the linear perturbations and their spatial structure in similarity space. All eigenmodes decay monotonically for 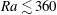$\mathit{Ra}\lesssim 360$, while for larger $\mathit{Ra}$ the dominant (slowest decaying or fastest growing) eigenmodes are oscillatory with waves propagating up the tail. Above a critical value 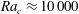$\mathit{Ra}_c \approx 10\, 000$, the steady solution becomes unstable to a limit cycle. A one-dimensional reduction to horizontally integrated quantities hints at a theoretical explanation for the oscillatory behaviour, but does not reproduce the loss of stability. Investigation of the initial transient at large $\mathit{Ra}$ reveals that an initially spherical thermal can rise 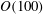$O(100)$ times its initial diameter before approaching its final self-similar shape. The presence of a rigid horizontal floor below the thermal makes a quantitative difference of around 10 % to the rate of rise at large 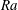$\mathit{Ra}$.

JFM classification

Convection: Convection Low-Reynolds-number flows: Low-Reynolds-number flows Convection: Plumes/thermals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 744 , 10 April 2014 , pp. 352 - 375
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blake, J. R. 1971 A note on the image system for a Stokeslet in a no-slip boundary. Proc. Camb. Phil. Soc. 70, 303–310.Google Scholar
Griffiths, R. W. 1986 Thermals in extremely viscous fluids, including the effects of temperature-dependent viscosity. J. Fluid Mech. 166, 115–138.CrossRefGoogle Scholar
Griffiths, R. W. 1991 Entrainment and stirring in viscous plumes. Phys. Fluids A 3, 1233–1242.Google Scholar
Lee, S. H. & Leal, L. G. 1982 The motion of a sphere in the presence of a deformable interface. II. A numerical study of the translation of a sphere normal to an interface. J. Colloid Interface Sci. 87, 81–106.Google Scholar
Lehoucq, R. B. & Sorensen, D. C. 1996 Deflation techniques for an implicitly restarted Arnoldi iteration. SIAM J. Matrix Anal. Appl. 17, 789–821.Google Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.Google Scholar
Leppinen, D. & Lister, J. R. 2003 Capillary pinch-off in inviscid fluids. Phys. Fluids 15, 568–578.Google Scholar
Morton, B. R. 1960 Weak thermal vortex rings. J. Fluid Mech. 9, 107–118.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Ribe, N. M., Davaille, A. & Christensen, U. R. 2007 Fluid dynamics of mantle plumes. In Mantle Plumes: A Multidisciplinary Approach (ed. Ritter, J. R. R & Christensen, U. R), pp. 1–48. Springer.Google Scholar
Roberts, G. O. 1977 Fast viscous convection. Geophys. Astrophys. Fluid Dyn 8, 197–233.Google Scholar
Schubert, G., Turcotte, D. L. & Olson, P. 2001 Mantle Convection in the Earth and Planets. Cambridge University Press.Google Scholar
Sierou, A. & Lister, J. R. 2003 Self-similar solutions for viscous capillary pinch-off. J. Fluid Mech. 497, 381–403.Google Scholar
Turner, J. S. 1969 Buoyant plumes and thermals. Annu. Rev. Fluid Mech. 1, 29–44.Google Scholar
Whittaker, R. J. & Lister, J. R. 2006a Steady axisymmetric creeping plumes above a planar boundary. Part 1. A point source. J. Fluid Mech. 567, 361–378.CrossRefGoogle Scholar
Whittaker, R. J. & Lister, J. R. 2006b Steady axisymmetric creeping plumes above a planar boundary. Part 2. A distributed source. J. Fluid Mech. 567, 379–397.CrossRefGoogle Scholar
Whittaker, R. J. & Lister, J. R. 2008 The self-similar rise of a buoyant thermal in very viscous flow. J. Fluid Mech. 606, 295–324.Google Scholar
Witelski, T. P. & Bernoff, A. J. 1999 Stability of self-similar solutions for van der Waals driven thin film rupture. Phys. Fluids 11, 2443–2445.CrossRefGoogle Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42, 391–412.Google Scholar
Worster, M. G. 1986 The axisymmetric laminar plume: asymptotic solution for large Prandtl number. Stud. Appl. Math. 75, 139–152.Google Scholar