Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-07-04T14:27:22.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Investigation of the pressure–strain-rate correlation and pressure fluctuations in convective and near neutral atmospheric surface layers

Published online by Cambridge University Press:  31 August 2018

Mengjie Ding ,
Khuong X. Nguyen ,
Shuaishuai Liu ,
Martin J. Otte  and
Chenning Tong Open the ORCID record for Chenning Tong [Opens in a new window]
Mengjie Ding
Affiliation:
Department of Mechanical Engineering, Clemson University, Clemson, SC 29634, USA
Khuong X. Nguyen
Affiliation:
Department of Mechanical Engineering, Clemson University, Clemson, SC 29634, USA
Shuaishuai Liu
Affiliation:
Department of Mechanical Engineering, Clemson University, Clemson, SC 29634, USA
Martin J. Otte
Affiliation:
Computer Science Corporation, Raleigh, NC 27603, USA
Chenning Tong*
Affiliation:
Department of Mechanical Engineering, Clemson University, Clemson, SC 29634, USA
*
†Email address for correspondence: ctong@clemson.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The pressure–strain-rate correlation and pressure fluctuations in convective and near neutral atmospheric surface layers are investigated. Their scaling properties, spectral characteristics, the contributions from the different source terms in the pressure Poisson equation and the effects of the wall are investigated using high-resolution (up to 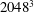$2048^{3}$) large-eddy simulation fields and through spectral predictions. The pressure–strain-rate correlation was found to have the mixed-layer and surface-layer scaling in the strongly convective and near neutral atmospheric surface layers, respectively. Its apparent surface-layer scaling in the moderately convective surface layer is due to the slow variations of the mixed-layer contribution, and is an inherent problem for single-point statistics in a multi-scale surface layer. In the strongly convective surface layer the pressure spectrum has an approximate 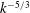$k^{-5/3}$ scaling range for small wavenumbers (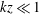$kz\ll 1$) due to the turbulent–turbulent contribution, and does not follow the surface-layer scaling, where 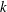$k$ and $z$ are the horizontal wavenumber and the distance from the surface respectively. The pressure–strain-rate cospectrum components have a 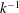$k^{-1}$ scaling range, consistent with our prediction using the surface layer parameters. It is dominated by the buoyancy contribution. Thus the anisotropy in the surface layer is due to the energy redistribution caused by the density fluctuations of the large eddies, rather than the turbulent–turbulent (inertial) effects. In the near neutral surface layer, the turbulent–turbulent and rapid contributions are primarily responsible for redistribution of energy from the streamwise velocity component to the vertical and spanwise components, respectively. The pressure–strain-rate cospectra peak near 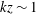$kz\sim 1$, and have some similarities to those in the strongly convective surface layer for 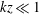$kz\ll 1$. For the moderately convective surface layer, the pressure–strain-rate cospectra change signs at scales of the order of the Obukhov length, thereby imposing it as a horizontal length scale in the surface layer. This result provides strong support to the multipoint Monin–Obukhov similarity recently proposed by Tong & Nguyen (J. Atmos. Sci., vol. 72, 2015, pp. 4337–4348). We further decompose the pressure into the free-space (infinite domain), the wall reflection and the harmonic contributions. In the strongly convective surface layer, the free-space contribution to the pressure–strain-rate correlation is dominated by the buoyancy part, and is the main cause of the surface-layer anisotropy. The wall reflection enhances the anisotropy for most of the surface layer, suggesting that the pressure source has a large coherence length. In the near neutral surface layer, the wall reflection is small, suggesting a much smaller source coherence length. The present study also clarifies the understanding of the role of the turbulent–turbulent pressure, and has implications for understanding the dynamics and structure as well as modelling the atmospheric surface layer.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence modelling
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 854 , 10 November 2018 , pp. 88 - 120
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balls, G. T. & Colella, P. 2002 A finite difference domain decomposition method using local corrections for the solution of Poisson’s equation. J. Comput. Phys. 180, 25–53.Google Scholar
Bradshaw, P. 1967 ‘Inactive’ motion and pressure fluctuations in turbulent boundary layers. J. Fluid Mech. 30, 241–258.Google Scholar
Brasseur, J. G. & Wei, T. 2010 Designing large-eddy simulation of the turbulent boundary layer to capture law-of-the-wall scaling. Phys. Fluids 22, 021303.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1988 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Crow, S. C. 1968 Viscoelastic properties of fine-grained incompressible turbulence. J. Fluid Mech. 33, 1–20.Google Scholar
Gibson, M. M. & Launder, B. E. 1978 Ground effects on pressure fluctuations in the atmospheric boundary layer. J. Fluid Mech. 86, 491–511.Google Scholar
Heinze, R., Dipankar, A., Henken, C. C., Moseley, C., Sourdeval, O., Trömel, S., Xie, X., Adamidis, P., Ament, F., Baars, H. et al. 2017 Large-eddy simulations over Germany using ICON: a comprehensive evaluation. Q. J. R. Meteorol. Soc. 143, 69–100.Google Scholar
James, R. A. 1977 The solution of Poisson’s equation for isolated source distributions. J. Comput. Phys. 25, 71–93.Google Scholar
Klemp, J. B. & Durran, D. R. 1983 An upper boundary condition permitting internal gravity wave radiation in numerical mesoscale models. Mon. Weath. Rev. 111, 430–444.Google Scholar
Kosović, B. 1997 Subgrid-scale modelling for the large-eddy simulation of high-Reynolds-number boundary layer. J. Fluid Mech. 336, 151–182.Google Scholar
Launder, B. E., Reece, G. J. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68, 537–566.Google Scholar
Lilly, D. K. 1967 The representation of small-scale turbulence in numerical simulation experiments. In Proc. IBM Scientific Computing Symp. on Environ. Sci. (ed. Goldstine, H. H.), pp. 195–210. IBM.Google Scholar
Lumley, J. L. & Newman, G. R. 1977 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 82, 161–178.Google Scholar
Miles, N. L., Wyngaard, J. C. & Otte, M. J. 2004 Turbulent pressure statistics in the atmospheric boundary layer from large-eddy simulation. Bound.-Layer Meteorol. 113, 161–185.Google Scholar
Mironov, D. V. 2001 Pressure-potential-temperature covariance in convection with rotation. Q. J. R. Meteorol. Soc. 127, 89–110.Google Scholar
Moeng, C. H. 1984 A large-eddy simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 41, 2052–2062.Google Scholar
Moeng, C. H. & Wyngaard, J. C. 1986 An analysis of closures for pressure-scalar covariances in the convective boundary layer. J. Atmos. Sci. 43, 2499–2513.Google Scholar
Moeng, C. H. & Wyngaard, J. C. 1988 Spectral analysis of large-eddy simulations of the convective boundary layer. J. Atmos. Sci. 45, 3573–3587.Google Scholar
Nguyen, K. X.2015 On subgrid-scale physics in the convective atmospheric surface layer. PhD dissertation, Department of Mechanical Engineering, Clemson University.Google Scholar
Nguyen, K. X., Horst, T. W., Oncley, S. P. & Tong, C. 2013 Measurements of the budgets of the subgrid-scale stress and temperature flux in a convective atmospheric surface layer. J. Fluid Mech. 729, 388–422.Google Scholar
Nguyen, K. X. & Tong, C. 2015 Investigation of subgrid-scale physics in the convective atmospheric surface layer using the budgets of the conditional mean subgrid-scale stress and temperature flux. J. Fluid Mech. 772, 295–329.Google Scholar
Otte, M. J. & Wyngaard, J. C. 2001 Stably stratified interfacial-layer turbulence from large-eddy simulation. J. Atmos. Sci. 58, 3424–3442.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rotta, J. C. 1951 Statistische theorie nichthomogener Turbulenz. Z. Phys. 129, 547–572.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. Part I. The basic equations. Mon. Weath. Rev. 91, 99–164.Google Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96, 297–324.Google Scholar
Stevens, R. J. A. M., Wilczek, M. & Meneveau, C. 2014 Large-eddy simulation study of the logarithmic law for second- and higher-order moments in turbulent wall-bounded flow. J. Fluid Mech. 757, 888–907.Google Scholar
Sullivan, P. P., McWilliams, J. C. & Moeng, C. H. 1994 A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorol. 71, 247–276.Google Scholar
Sullivan, P. P., McWilliams, J. C. & Moeng, C. H. 1996 A grid nesting method for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorol. 80, 167–202.Google Scholar
Sullivan, P. P. & Patton, E. G. 2011 The effect of mesh resolution on convective boundary layer statistics and structures generated by large-eddy simulation. J. Atmos. Sci. 68, 2395–2415.Google Scholar
Tong, C. & Nguyen, K. X. 2015 Multipoint Monin–Obukhov similarity and its application to turbulence spectra in the convective atmospheric surface layer. J. Atmos. Sci. 72, 4337–4348.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flows. Cambridge University Press.Google Scholar
Wyngaard, J. C. 1992 Atmosperic turbulence. Annu. Rev. Fluid Mech. 24, 205–233.Google Scholar
Wyngaard, J. C. & Coté, O. R. 1971 The budgets of turbulent kinetic energy and temperature variance in the atmospheric surface layer. J. Atmos. Sci. 28, 190–201.Google Scholar
Wyngaard, J. C., Coté, O. R. & Izumi, Y. 1971 Local free convection, similarity, and the budgets of shear stress and heat flux. J. Atmos. Sci. 28, 1171–1182.Google Scholar