Hostname: page-component-68945f75b7-qf55q Total loading time: 0 Render date: 2024-08-06T09:12:15.531Z Has data issue: false hasContentIssue false
  • English
  • Français

The lid-driven right-angled isosceles triangular cavity flow

Published online by Cambridge University Press:  22 July 2019

B. An ,
J. M. Bergada  and
F. Mellibovsky Open the ORCID record for F. Mellibovsky [Opens in a new window]
B. An
Affiliation:
Department of Fluid Mechanics, Universitat Politècnica de Catalunya, 08034, Barcelona, Spain
J. M. Bergada
Affiliation:
Department of Fluid Mechanics, Universitat Politècnica de Catalunya, 08034, Barcelona, Spain
F. Mellibovsky*
Affiliation:
Department of Physics, Aerospace Engineering Division, Universitat Politècnica de Catalunya, 08034, Barcelona, Spain
*
†Email address for correspondence: fernando.mellibovsky@upc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

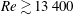We employ lattice Boltzmann simulation to numerically investigate the two-dimensional incompressible flow inside a right-angled isosceles triangular enclosure driven by the tangential motion of its hypotenuse. While the base flow, directly evolved from creeping flow at vanishing Reynolds number, remains stationary and stable for flow regimes beyond $Re\gtrsim 13\,400$, chaotic motion is nevertheless observed from as low as 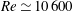$Re\simeq 10\,600$. Chaotic dynamics is shown to arise from the destabilisation, following a variant of the classic Ruelle–Takens route, of a secondary solution branch that emerges at a relatively low 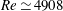$Re\simeq 4908$ and appears to bear no connection to the base state. We analyse the bifurcation sequence that takes the flow from steady to periodic and then quasi-periodic and show that the invariant torus is finally destroyed in a period-doubling cascade of a phase-locked limit cycle. As a result, a strange attractor arises that induces chaotic dynamics.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Nonlinear Dynamical Systems: Chaos
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 875 , 25 September 2019 , pp. 476 - 519
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abouhamza, A. & Pierre, R. 2003 A neutral stability curve for incompressible flows in a rectangular driven cavity. Math. Comput. Model. 38 (1–2), 141–157.Google Scholar
Afraimovich, V. S. & Shilnikov, L. P. 1983 On invariant two-dimensional tori, their breakdown and stochasticity. In Methods of Qualitative Theory of Differential Equations, pp. 3–26. Gorki University Press.Google Scholar
Ahmed, M. & Kuhlmann, H. C. 2012 Flow instability in triangular lid-driven cavities with wall motion away from a rectangular corner. Fluid Dyn. Res. 44 (2), 025501.Google Scholar
Aidun, C. K., Triantafillopoulos, N. G. & Benson, J. D. 1991 Global stability of a lid-driven cavity with throughflow – flow visualization studies. Phys. Fluids A 3 (9), 2081–2091.Google Scholar
Albensoeder, S., Kuhlmann, H. C. & Rath, H. J. 2001 Three-dimensional centrifugal-flow instabilities in the lid-driven-cavity problem. Phys. Fluids 13 (1), 121–135.Google Scholar
Anischenko, V. S., Safonova, M. A. & Chua, L. O. 1993 Confirmation of the Afraimovich-Shilnikov torus-breakdown theorem via a torus circuit. IEEE Trans. Cir. Sys. 40 (11), 792–800.Google Scholar
Auteri, F., Parolini, N. & Quartapelle, L. 2002 Numerical investigation on the stability of singular driven cavity flow. J. Comput. Phys. 183 (1), 1–25.Google Scholar
Auteri, F., Quartapelle, L. & Vigevano, L. 2002 Accurate omega-psi spectral solution of the singular driven cavity problem. J. Comput. Phys. 180 (2), 597–615.Google Scholar
Batchelor, G. K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1 (2), 177–190.Google Scholar
Batoul, A., Khallouf, H. & Labrosse, G. 1994 A direct spectral solver of the 2D/3D unsteady Stokes problem – application to the 2D square driven cavity. C. R. Acad. Sci. II 319 (12, 1), 1455–1461.Google Scholar
Benson, J. D. & Aidun, C. K. 1992 Transition to unsteady nonperiodic state in a through-flow lid-driven cavity. Phys. Fluids A 4 (10), 2316–2319.Google Scholar
Bhatnagar, P. L., Gross, E. P. & Krook, M. 1954 A model for collision processes in gases. 1. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94 (3), 511–525.Google Scholar
Boffetta, G. & Ecke, R. E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44, 427–451.Google Scholar
Boppana, V. B. L. & Gajjar, J. S. B. 2010 Global flow instability in a lid-driven cavity. Intl J. Numer. Meth. Fluids 62 (8), 827–853.Google Scholar
Botella, O. 1997 On the solution of the Navier–Stokes equations using Chebyshev projection schemes with third-order accuracy in time. Comput. Fluids 26 (2), 107–116.Google Scholar
Botella, O. & Peyret, R. 1998 Benchmark spectral results on the lid-driven cavity flow. Comput. Fluids 27 (4), 421–433.Google Scholar
Botella, O. & Peyret, R. 2001 Computing singular solutions of the Navier–Stokes equations with the Chebyshev-collocation method. Intl J. Numer. Meth. Fluids 36 (2), 125–163.Google Scholar
Bruneau, C. H. & Saad, M. 2006 The 2D lid-driven cavity problem revisited. Comput. Fluids 35 (3), 326–348.Google Scholar
Burggraf, O. R. 1966 Analytical and numerical studies of structure of steady separated flows. J. Fluid Mech. 24 (1), 113–151.Google Scholar
Cazemier, W., Verstappen, R. W. C. P. & Veldman, A. E. P. 1998 Proper orthogonal decomposition and low-dimensional models for driven cavity flows. Phys. Fluids 10 (7), 1685–1699.Google Scholar
Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30, 329–364.Google Scholar
Cheng, M. & Hung, K. C. 2006 Vortex structure of steady flow in a rectangular cavity. Comput. Fluids 35 (10), 1046–1062.Google Scholar
Cornubert, R., d’Humières, D. & Levermore, D. 1991 A Knudsen layer theory for lattice gases. Physica D 47 (1-2), 241–259.Google Scholar
d’Humières, D. 1992 Generalized lattice-Boltzmann equations. In Rarefied Gas Dynamics: Theory and Simulations (ed. Weaver, D. P. & Shizgal, B. D.), Progress in Astronautics and Aeronautics, vol. 159, pp. 450–458. American Institute of Aeronautics and Astronautics.Google Scholar
Ding, Y. & Kawahara, M. 1999 Three-dimensional linear stability analysis of incompressible viscous flows using the finite element method. Intl J. Numer. Meth. Fluids 31 (2), 451–479.Google Scholar
Du, R., Shi, B. & Chen, X. 2006 Multi-relaxation-time lattice Boltzmann model for incompressible flow. Phys. Lett. A 359 (6), 564–572.Google Scholar
Erturk, E. & Gokcol, C. 2006 Fourth-order compact formulation of Navier–Stokes equations and driven cavity flow at high Reynolds numbers. Intl J. Numer. Meth. Fluids 50 (4), 421–436.Google Scholar
Erturk, E. & Gokcol, O. 2007 Fine grid numerical solutions of triangular cavity flow. Eur. Phys. J. 38 (1), 97–105.Google Scholar
Fortin, A., Jardak, M., Gervais, J. J. & Pierre, R. 1997 Localization of Hopf bifurcations in fluid flow problems. Intl J. Numer. Meth. Fluids 24 (11), 1185–1210.Google Scholar
Gaskell, P. H., Thompson, H. M. & Savage, M. D. 1999 A finite element analysis of steady viscous flow in triangular cavities. Proc. Inst. Mech. Engrs 213 (3), 263–276.Google Scholar
Ghia, U., Ghia, K. N. & Shin, C. T. 1982 High-Re solutions for incompressible-flow using the Navier–Stokes equations and a multigrid method. J. Comput. Phys. 48 (3), 387–411.Google Scholar
Gonzalez, L. M., Ahmed, M., Kuehnen, J., Kuhlmann, H. C. & Theofilis, V. 2011 Three-dimensional flow instability in a lid-driven isosceles triangular cavity. J. Fluid Mech. 675, 369–396.Google Scholar
Goodrich, J. W., Gustafson, K. & Halasi, K. 1990 Hopf-bifurcation in the driven cavity. J. Comput. Phys. 90 (1), 219–261.Google Scholar
Gresho, P. M. & Chan, S. T. 1990 On the theory of semi-implicit projection methods for viscous incompressible-flow and its implementation via a finite-element method that also introduces a nearly consistent mass matrix. 2. Implementation. Intl J. Numer. Meth. Fluids 11 (5), 621–659.Google Scholar
Guo, Z. L., Shi, B. C. & Wang, N. C. 2000 Lattice BGK model for incompressible Navier–Stokes equation. J. Comput. Phys. 165 (1), 288–306.Google Scholar
Guo, Z. L., Zheng, C. G. & Shi, B. C. 2002 An extrapolation method for boundary conditions in lattice Boltzmann method. Phys. Fluids 14 (6), 2007–2010.Google Scholar
Guo, Z. L., Zheng, C. G. & Shi, B. C. 2002 Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method. Chin. Phys. 11 (4), 366–374.Google Scholar
Gupta, M. M. & Kalita, J. C. 2005 A new paradigm for solving Navier–Stokes equations: streamfunction-velocity formulation. J. Comput. Phys. 207 (1), 52–68.Google Scholar
Gupta, M. M., Manohar, R. P. & Noble, B. 1981 Nature of viscous flows near sharp corners. Comput. Fluids 9 (4), 379–388.Google Scholar
Hof, B., van Doorne, C. W. H., Westerweel, J., Nieuwstadt, F. T. M., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 305 (5690), 1594–1598.Google Scholar
Hou, S. L., Zou, Q., Chen, S. Y., Doolen, G. & Cogley, A. C. 1995 Simulation of cavity flow by the lattice Boltzmann method. J. Comput. Phys. 118 (2), 329–347.Google Scholar
Jagannathan, A., Mohan, R. & Dhanak, M. 2014 A spectral method for the triangular cavity flow. Comput. Fluids 95, 40–48.Google Scholar
Jimenez, J. 1990 Transition to turbulence in 2-dimensional Poiseuille flow. J. Fluid Mech. 218, 265–297.Google Scholar
Jyotsna, R. & Vanka, S. P. 1995 Multigrid calculation of steady, viscous-flow in a triangular cavity. J. Comput. Phys. 122 (1), 107–117.Google Scholar
Kalita, J. C. & Gogoi, B. B. 2016 A biharmonic approach for the global stability analysis of 2D incompressible viscous flows. Appl. Math. Model. 40 (15–16), 6831–6849.Google Scholar
Kawaguti, M. 1961 Numerical solution of Navier–Stokes equations for flow in a 2-dimensional cavity. J. Phys. Soc. Japan 16 (11), 2307.Google Scholar
Khorasanizade, S. & Sousa, J. M. M. 2014 A detailed study of lid-driven cavity flow at moderate Reynolds numbers using incompressible SPH. Intl J. Numer. Meth. Fluids 76 (10), 653–668.Google Scholar
Kohno, H. & Bathe, K. J. 2006 A flow-condition-based interpolation finite element procedure for triangular grids. Intl J. Numer. Meth. Fluids 51 (6), 673–699.Google Scholar
Koseff, J. R. & Street, R. L. 1984 The lid-driven cavity flow – a synthesis of qualitative and quantitative observations. Trans. ASME J. Fluids Engng 106 (4), 390–398.Google Scholar
Krupa, M. 1990 Bifurcations of relative equilibria. SIAM J. Math. Anal. 21 (6), 1453–1486.Google Scholar
Kuhlmann, H.C. & Romanò, F. 2019 The lid-driven cavity. In Computational modelling of bifurcations and instabilities in fluid dynamics (ed. Gelfgat, A.), chap. 8, pp. 233–309. Springer.Google Scholar
Lallemand, P. & Luo, L. S. 2000 Theory of the lattice Boltzmann method: dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 61 (6, A), 6546–6562.Google Scholar
Li, M. & Tang, T. 1996 Steady viscous flow in a triangular cavity by efficient numerical techniques. Comput. Maths Applics. 31 (10), 55–65.Google Scholar
Lin, L. S., Chang, H. W. & Lin, C. A. 2013 Multi relaxation time lattice Boltzmann simulations of transition in deep 2D lid driven cavity using GPU. Comput. Fluids 80 (SI), 381–387.Google Scholar
Lopez, J. M., Welfert, B. D., Wu, K. & Yalim, J. 2017 Transition to complex dynamics in the cubic lid-driven cavity. Phys. Rev. Fluids 2 (7), 074401.Google Scholar
de Lozar, A., Mellibovsky, F., Avila, M. & Hof, B. 2012 Edge state in pipe flow experiments. Phys. Rev. Lett. 108 (21), 214502.Google Scholar
Marchi, C. H., Suero, R. & Araki, L. K. 2009 The lid-driven square cavity flow: numerical solution with a 1024 × 1024 grid. J. Braz. Soc. Mech. Sci. Engng 31 (3), 186–198.Google Scholar
McQuain, W. D., Ribbens, C. J., Wang, C. Y. & Watson, L. T. 1994 Steady viscous-flow in a trapezoidal cavity. Comput. Fluids 23 (4), 613–626.Google Scholar
Mellibovsky, F. & Meseguer, A. 2015 A mechanism for streamwise localisation of nonlinear waves in shear flows. J. Fluid Mech. 779, R1.Google Scholar
Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18 (1), 1–18.Google Scholar
Molenaar, D., Clercx, H. J. H. & van Heijst, G. J. F. 2005 Transition to chaos in a confined two-dimensional fluid flow. Phys. Rev. Lett. 95 (10), 104503.Google Scholar
Murdock, J. R., Ickes, J. C. & Yang, S. L. 2017 Transition flow with an incompressible lattice Boltzmann method. Adv. Appl. Maths Mech. 9 (5), 1271–1288.Google Scholar
Newhouse, S., Ruelle, D. & Takens, F. 1978 Occurrence of strange Axiom A attractors near quasi periodic flows on T m , m ≧ 3. Commun. Math. Phys. 64 (1), 35–40.Google Scholar
Non, E., Pierre, R. & Gervais, J. J. 2006 Linear stability of the three-dimensional lid-driven cavity. Phys. Fluids 18 (8), 084103.Google Scholar
Nuriev, A. N., Egorov, A. G. & Zaitseva, O. N. 2016 Bifurcation analysis of steady-state flows in the lid-driven cavity. Fluid Dynam. Res. 48 (6), 6th International Symposium on Instability and Bifurcations in Fluid Dynamics (BIFD), ESPCI, Paris, France, Jul 15–17, 2015.Google Scholar
Ozalp, C., Pinarbasi, A. & Sahin, B. 2010 Experimental measurement of flow past cavities of different shapes. Exp. Therm. Fluid Sci. 34 (5), 505–515.Google Scholar
Pan, F. & Acrivos, A. 1967 Steady flows in rectangular cavities. J. Fluid Mech. 28 (4), 643.Google Scholar
Paramane, S. B. & Sharma, A. 2008 Consistent implementation and comparison of FOU, CD, SOU, and QUICK convection schemes on square, skew, trapezoidal, and triangular lid-driven cavity flow. Numer. Heat Transfer 54 (1), 84–102.Google Scholar
Pasquim, B. M. & Mariani, V. C. 2008 Solutions for incompressible viscous flow in a triangular cavity using cartesian grid method. Comput. Model. Engng Sci. 35 (2), 113–132.Google Scholar
Peng, Y. F., Shiau, Y. H. & Hwang, R. R. 2003 Transition in a 2-D lid-driven cavity flow. Comput. Fluids 32 (3), 337–352.Google Scholar
Poliashenko, M. & Aidun, C. K. 1995 A direct method for computation of simple bifurcations. J. Comput. Phys. 121 (2), 246–260.Google Scholar
Prandtl, L. 1904 über Flüssigkeitsbewegung bei sehr kleiner Reibung. In Verhandl III, Intern. Math. Kongr. Heidelberg, Auch: Gesammelte Abhandlungen, pp. 484–491.Google Scholar
Procaccia, I. 1988 Universal properties of dynamically complex-systems – the organization of chaos. Nature 333 (6174), 618–623.Google Scholar
Qian, Y. H., D’Humières, D. & Lallemand, P. 1992 Lattice BGK models for Navier–Stokes equation. Eur. Phys. Lett. 17 (6BIS), 479–484.Google Scholar
Ribbens, C. J., Watson, L. T. & Wang, C. Y. 1994 Steady viscous-flow in a triangular cavity. J. Comput. Phys. 112 (1), 173–181.Google Scholar
Romanò, F. & Kuhlmann, H. C. 2017 Smoothed-profile method for momentum and heat transfer in particulate flows. Intl J. Numer. Meth. Fluids 83 (6), 485–512.Google Scholar
Ruelle, D. & Takens, F. 1971 On the nature of turbulence. Commun. Math. Phys. 20 (3), 167–192.Google Scholar
Sahin, M. & Owens, R. G. 2003 A novel fully implicit finite volume method applied to the lid-driven cavity problem. Part I. High Reynolds number flow calculations. Intl J. Numer. Meth. Fluids 42 (1), 57–77.Google Scholar
Sahin, M. & Owens, R. G. 2003 A novel fully-implicit finite volume method applied to the lid-driven cavity problem. Part II. Linear stability analysis. Intl J. Numer. Meth. Fluids 42 (1), 79–88.Google Scholar
Schreiber, R. & Keller, H. B. 1983 Driven cavity flows by efficient numerical techniques. J. Comput. Phys. 49 (2), 310–333.Google Scholar
Shankar, P. N. & Deshpande, M. D. 2000 Fluid mechanics in the driven cavity. Annu. Rev. Fluid Mech. 32, 93–136.Google Scholar
Shen, J. 1991 Hopf-bifurcation of the unsteady regularized driven cavity flow. J. Comput. Phys. 95 (1), 228–245.Google Scholar
Sidik, N. A. C. & Munir, F. A. 2012 Mesoscale numerical prediction of fluid flow in a shear driven cavity. Arab. J. Sci. Engng 37 (6), 1723–1735.Google Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96 (17), 174101.Google Scholar
Smith, J. A. & Largier, J. L. 1995 Observations of nearshore circulation – rip currents. J. Geophys. Res.-Oceans 100 (C6), 10967–10975.Google Scholar
Theofilis, V., Duck, P. W. & Owen, J. 2004 Viscous linear stability analysis of rectangular duct and cavity flows. J. Fluid Mech. 505, 249–286.Google Scholar
Tiesinga, G., Wubs, F. W. & Veldman, A. E. P. 2002 Bifurcation analysis of incompressible flow in a driven cavity by the Newton–Picard method. J. Comput. Appl. Maths 140 (1–2 SI), 751–772; 9th International Congress on Computational and Applied Mathematics, Univ. Leuven, Leuven, Belgium, Jul 17–21, 2000.Google Scholar
Vanka, S. P. 1986 Block-implicit multigrid solution of Navier–Stokes equations in primitive variables. J. Comput. Phys. 65 (1), 138–158.Google Scholar
Wells, M. G. & van Heijst, G. J. F. 2003 A model of tidal flushing of an estuary by dipole formation. Dyn. Atmos. Oceans 37 (3), 223–244.Google Scholar
Yu, D. Z., Mei, R. W., Luo, L. S. & Shyy, W. 2003 Viscous flow computations with the method of lattice Boltzmann equation. Prog. Aerosp. Sci. 39 (5), 329–367.Google Scholar
Zhang, T., Shi, B. & Chai, Z. 2010 Lattice Boltzmann simulation of lid-driven flow in trapezoidal cavities. Comput. Fluids 39 (10), 1977–1989.Google Scholar
Zhuo, C., Zhong, C. & Cao, J. 2013 Filter-matrix lattice Boltzmann simulation of lid-driven deep-cavity flows. Part II. Flow bifurcation. Comput. Maths Applics. 65 (12), 1883–1893.Google Scholar
Ziegler, D. P. 1993 Boundary-conditions for lattice Boltzmann simulations. J. Stat. Phys. 71 (5–6), 1171–1177.Google Scholar
Zou, Q. S. & He, X. Y. 1997 On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 9 (6), 1591–1598.Google Scholar

An et al. supplementary movie 1

Re=8500. B-type periodic solution

Download An et al. supplementary movie 1(Video)
Video 81.2 KB

An et al. supplementary movie 2

Re=14000. A-type periodic solution

Download An et al. supplementary movie 2(Video)
Video 13.5 KB

An et al. supplementary movie 3

Re=9000. B-type quasiperiodic solution

Download An et al. supplementary movie 3(Video)
Video 787.7 KB

An et al. supplementary movie 4

Re=10500. B-type phase-locked quasiperiodic solution

Download An et al. supplementary movie 4(Video)
Video 1.9 MB

An et al. supplementary movie 5

Re=11000. B-type chaotic solution

Download An et al. supplementary movie 5(Video)
Video 1.3 MB

An et al. supplementary movie 6

Re=12000. Chaotic solution

Download An et al. supplementary movie 6(Video)
Video 2.9 MB