Hostname: page-component-68945f75b7-9klrw Total loading time: 0 Render date: 2024-08-05T12:20:28.620Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean dynamics of transitional boundary-layer flow

Published online by Cambridge University Press:  19 July 2011

J. KLEWICKI ,
R. EBNER  and
X. WU
J. KLEWICKI*
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
R. EBNER
Affiliation:
Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
X. WU
Affiliation:
Department of Mechanical Engineering, Royal Military College of Canada, Kingston, Ontario, CanadaK7K 7B4
*
†Email address for correspondence: joe.klewicki@unh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamical mechanisms underlying the redistribution of mean momentum and vorticity are explored for transitional two-dimensional boundary-layer flow at nominally zero pressure gradient. The analyses primarily employ the direct numerical simulation database of Wu & Moin (J. Fluid Mech., vol. 630, 2009, p. 5), but are supplemented with verifications utilizing subsequent similar simulations. The transitional regime is taken to include both an instability stage, which effectively generates a finite Reynolds stress profile, −ρuv(y), and a nonlinear development stage, which progresses until the terms in the mean momentum equation attain the magnitude ordering of the four-layer structure revealed by Wei et al. (J. Fluid Mech., vol. 522, 2005, p. 303). Self-consistently applied criteria reveal that the third layer of this structure forms first, followed by layers IV and then II and I. For the present flows, the four-layer structure is estimated to be first realized at a momentum thickness Reynolds number Rθ = U∞ θ/ν ≃ 780. The first-principles-based theory of Fife et al. (J. Disc. Cont. Dyn. Syst. A, vol. 24, 2009, p. 781) is used to describe the mean dynamics in the laminar, transitional and four-layer regimes. As in channel flow, the transitional regime is marked by a non-negligible influence of all three terms in the mean momentum equation at essentially all positions in the boundary layer. During the transitional regime, the action of the Reynolds stress gradient rearranges the mean viscous force and mean advection profiles. This culminates with the segregation of forces characteristic of the four-layer regime. Empirical and theoretical evidence suggests that the formation of the four-layer structure also underlies the emergence of the mean dynamical properties characteristic of the high-Reynolds-number flow. These pertain to why and where the mean velocity profile increasingly exhibits logarithmic behaviour, and how and why the Reynolds stress distribution develops such that the inner normalized position of its peak value, ym+, exhibits a Reynolds number dependence according to .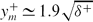

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent transition
Type
Papers
Information
Journal of Fluid Mechanics , Volume 682 , 10 September 2011 , pp. 617 - 651
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adrian, R. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
Afzal, N. 1982 Fully developed turbulent flow in a pipe: an intermediate layer. Ing.-Arch. 52, 355–377.CrossRefGoogle Scholar
Antonia, R., Teitel, M., Kim, J. & Browne, L. 1992 Low-Reynolds-number effects in a fully developed turbulent channel flow. J. Fluid Mech. 236, 579–605.CrossRefGoogle Scholar
Bailey, S., Hultmark, M., Smits, A. & Schultz, M. 2008 Azimuthal structure of turbulence in high Reynolds number pipe flow. J. Fluid Mech. 615, 121–138.CrossRefGoogle Scholar
Balakumar, B. & Adrian, R. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google ScholarPubMed
Buschmann, M., Indinger, T. & Gad-el-Hak, M. 2009 Near-wall behavior of turbulent wall-bounded flows. Intl J. Heat Fluid Flow 30, 993–1006.CrossRefGoogle Scholar
Ching, C. Y., Djendi, L. & Antonia, R. A. 1995 Low Reynolds-number effects in a turbulent boundary layer. Exp. Fluids 19, 61–68.CrossRefGoogle Scholar
Criminale, W., Jackson, T. & Joslin, R. 2003 Theory and Computation in Hydrodynamic Stability. Cambridge University Press.CrossRefGoogle Scholar
Dean, R. 1978 Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. J. Fluids Engng 100, 215–223.CrossRefGoogle Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.CrossRefGoogle Scholar
Elsnab, J., Klewicki, J., Maynes, D. & Ameel, T. 2011 Mean dynamics of transitional channel flow. J. Fluid Mech. 678, 451–481.CrossRefGoogle Scholar
Elsnab, J., Maynes, D., Klewicki, J. & Ameel, T. 2010 Mean flow structure in high aspect ratio microchannel flows. Exp. Therm. Fluid Sci. 34, 1077–1088.CrossRefGoogle Scholar
Eyink, G. 2008 Turbulent flow in pipes and channels as cross-stream ‘inverse cascades’ of vorticity. Phys. Fluids 20, 125101.CrossRefGoogle Scholar
Fife, P., Klewicki, J., McMurtry, P. & Wei, T. 2005 a Multiscaling in the presence of indeterminacy: wall-induced turbulence. Multiscale Model. Simul. 4, 936–959.CrossRefGoogle Scholar
Fife, P., Klewicki, J. & Wei, T. 2009 Time averaging in turbulence settings may reveal an infinite hierarchy of length scales. J. Discrete Continuous Dyn. Syst. 24, 781–807.CrossRefGoogle Scholar
Fife, P., Wei, T., Klewicki, J. & McMurtry, P. 2005 b Stress gradient balance layers and scale hierarchies in wall bounded turbulent flows. J. Fluid Mech. 532, 165–189.CrossRefGoogle Scholar
Ganapathisubramani, B. 2008 Statistical structure of momentum sources and sinks in the outer region of a turbulent boundary layer. J. Fluid Mech. 606, 225–237.CrossRefGoogle Scholar
Guala, M., Hommema, S. & Adrian, R. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Hoyas, S. & Jimenez, J. 2006 Scaling the velocity fluctuations in turbulent channels up to Re τ = 2003. Phys. Fluids 18, 011702.CrossRefGoogle Scholar
Jordinson, R. 1970 The flat plate boundary layer. Part 1. Numerical integration of the Orr–Sommerfeld equation. J. Fluid Mech. 43, 801–811.CrossRefGoogle Scholar
Klewicki, J. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. J. Fluids Engng 132, 094001.CrossRefGoogle Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.CrossRefGoogle Scholar
Klewicki, J., Fife, P., Wei, T. & McMurtry, P. 2007 A physical model of the turbulent boundary layer consonant with mean momentum balance structure. Phil. Trans. R. Soc. Lond. A 365, 823–839.Google ScholarPubMed
Kuroda, A., Kasagi, N. & Hirata, M. 1989 A direct numerical simulation of the fully developed turbulent channel flow. In Proc. Intl Symp. on Computational Fluid Dynamics, Nagoya, Japan, pp. 1174–1179.Google Scholar
Laadhari, F. 2002 On the evolution of maximum turbulent kinetic energy production in a channel flow. Phys. Fluids 14, L65–L68.CrossRefGoogle Scholar
Long, R. & Chen, T.-C. 1981 Experimental evidence for the existence of the mesolayer in turbulent systems. J. Fluid Mech. 105, 19–59.CrossRefGoogle Scholar
Marusic, I. 2009 Unraveling turbulence near walls. J. Fluid Mech. 630, 1–4.CrossRefGoogle Scholar
Metzger, M., Adams, P. & Fife, P. 2008 Mean momentum balance in moderately favourable pressure gradient turbulent boundary layers. J. Fluid Mech. 617, 107–140.CrossRefGoogle Scholar
Monkewitz, P., Chauhan, K. & Nagib, H. 2008 Comparison of mean flow similarity laws in zero-pressure-gradient turbulent boundary layers. Phys. Fluids 20, 105102.CrossRefGoogle Scholar
Monty, J., Stewart, J., Williams, R. & Chong, M. 1981 Large scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.CrossRefGoogle Scholar
Nagib, H. & Chauhan, K. 2008 Variation of von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.CrossRefGoogle Scholar
Nagib, H., Chauhan, K. & Mokewitz, P. 2007 Approach to an asymptotic state for zero pressure gradient turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 365, 755–770.Google Scholar
Osterlund, J., Johansson, A., Nagib, H. & Hites, M. 2000 A note on the overlap region in turbulent boundary layers. Phys. Fluids 12, 1–4.CrossRefGoogle Scholar
Perry, A. & Chong, M. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Schlatter, P. & Orlu, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2000 Boundary Layer Theory. Springer.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
Sherman, F. 1990 Viscous Flows. McGraw-Hill.Google Scholar
Smits, A., McKeon, B. & Marusic, I. 2011 High Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 253–375.CrossRefGoogle Scholar
Sreenivasan, K. 1989 The turbulent boundary layer. In Frontiers in Experimental Fluid Mechanics (ed. Gad-el-Hak, M.), pp. 159–209. Springer.CrossRefGoogle Scholar
Sreenivasan, K. & Bershadskii, A. 2006 Finite-Reynolds-number effects in turbulence using logarithmic expansions. J. Fluid Mech. 554, 477–498.CrossRefGoogle Scholar
Sreenivasan, K. & Sahay, A. 1997 The persistence of viscous effects in the overlap region and the mean velocity in turbulent pipe and channel flows. In Self-Sustaining Mechanisms of Wall Turbulence (ed. Panton, R.), pp. 253–272. Computational Mechanics Publications.Google Scholar
Tomkins, C. & Adrian, R. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Townsend, A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 7, 883–900.CrossRefGoogle Scholar
Wei, T., Fife, P. & Klewicki, J. 2007 On scaling the mean momentum balance and its solutions in turbulent Couette–Poiseuille flow. J. Fluid Mech. 573, 371–398.CrossRefGoogle Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 a Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar
Wei, T., McMurtry, P., Klewicki, J. & Fife, P. 2005 b Mesoscaling of the Reynolds shear stress in turbulent channel and pipe flows. AIAA J. 43, 2350–2353.CrossRefGoogle Scholar
Wu, X. 2010 Establishing the generality of three phenomena using a boundary layer with free-stream passing wakes. J. Fluid Mech. 664, 193–219.CrossRefGoogle Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.CrossRefGoogle Scholar
Wu, X. & Moin, P. 2010 Transitional and turbulent boundary layer with heat transfer. Phys. Fluids 22, 085105.CrossRefGoogle Scholar