Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-25T00:29:16.490Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal energy thresholds for sustained turbulent bands in channel flow

Published online by Cambridge University Press:  18 May 2022

E. Parente Open the ORCID record for E. Parente [Opens in a new window] ,
J.-Ch. Robinet Open the ORCID record for J.-Ch. Robinet [Opens in a new window] ,
P. De Palma Open the ORCID record for P. De Palma [Opens in a new window]  and
S. Cherubini Open the ORCID record for S. Cherubini [Opens in a new window]
E. Parente*
Affiliation:
DynFluid - Arts et Métiers Paris, 151 Bd de l'Hôpital, 75013 Paris, France Dipartimento di Meccanica, Matematica e Management (DMMM), Politecnico di Bari, Via Re David 200, 70126 Bari, Italy
J.-Ch. Robinet
Affiliation:
DynFluid - Arts et Métiers Paris, 151 Bd de l'Hôpital, 75013 Paris, France
P. De Palma
Affiliation:
Dipartimento di Meccanica, Matematica e Management (DMMM), Politecnico di Bari, Via Re David 200, 70126 Bari, Italy
S. Cherubini
Affiliation:
Dipartimento di Meccanica, Matematica e Management (DMMM), Politecnico di Bari, Via Re David 200, 70126 Bari, Italy
*
†Email address for correspondence: enzaparente@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

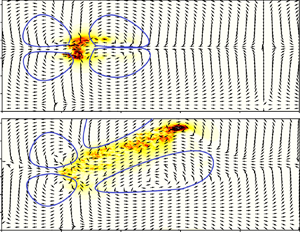
In this work, nonlinear variational optimization is used for obtaining minimal seeds for the formation of turbulent bands in channel flow. Using nonlinear optimization together with energy bisection, we have found that the minimal energy threshold for obtaining spatially patterned turbulence scales with $Re^{-8.5}$ for $Re>1000$. The minimal seed, which is different to that found in a much smaller domain, is characterized by a spot-like structure surrounded by a low-amplitude large-scale quadrupolar flow filling the whole domain. This minimal-energy perturbation of the laminar flow has dominant wavelengths close to $4$ in the streamwise direction and $1$ in the spanwise direction, and is characterized by a spatial localization increasing with the Reynolds number. At $Re \lesssim 1200$, the minimal seed evolves in time, creating an isolated oblique band, whereas for $Re\gtrsim 1200$, a quasi-spanwise-symmetric evolution is observed, giving rise to two distinct bands. A similar evolution is found also at low $Re$ for non-minimal optimal perturbations. This highlights two different mechanisms of formation of turbulent bands in channel flow, depending on the Reynolds number and initial energy of the perturbation. The selection of one of these two mechanisms appears to be dependent on the probability of decay of the newly created stripe, which increases with time, but decreases with the Reynolds number.

JFM classification

Instability: Nonlinear instability Instability: Shear-flow instability Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 942 , 10 July 2022 , A18
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aida, H., Tsukahara, T. & Kawaguchi, Y. 2010 DNS of turbulent spot developing into turbulent stripe in plane Poiseuille flow. In Fluids Engineering Division Summer Meeting, pp. 2125–2130. ASME Digital Collection.CrossRefGoogle Scholar
Aida, H., Tsukahara, T. & Kawaguchi, Y. 2011 Development of a turbulent spot into a stripe pattern in plane Poiseuille flow. arxiv:1410.0098.Google Scholar
Alavyoon, F., Henningson, D.S. & Alfredsson, P.H. 1986 Turbulent spots in plane Poiseuille flow visualization. Phys. Fluids 29 (4), 1328–1331.CrossRefGoogle Scholar
Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333 (6039), 192–196.CrossRefGoogle ScholarPubMed
Barkley, D. & Tuckerman, L.S. 2005 Computational study of turbulent laminar patterns in Couette flow. Phys. Rev. Lett. 94 (1), 014502.CrossRefGoogle ScholarPubMed
Brand, E. & Gibson, J.F. 2014 A doubly localized equilibrium solution of plane Couette flow. J. Fluid Mech. 750, R3.CrossRefGoogle Scholar
Bullister, E.T. & Orszag, S.A. 1987 Numerical simulation of turbulent spots in channel and boundary layer flows. J. Sci. Comput. 2, 263–281.CrossRefGoogle Scholar
Carlson, D.R., Widnall, S.E. & Peeters, M.F. 1982 A flow-visualization study of transition in plane Poiseuille flow. J. Fluid Mech. 121, 487–505.CrossRefGoogle Scholar
Chantry, M., Tuckerman, L.S. & Barkley, D. 2016 Turbulent–laminar patterns in shear flows without walls. J. Fluid. Mech. 791, R8.CrossRefGoogle Scholar
Cherubini, S., De Palma, P. & Robinet, J.-C. 2015 Nonlinear optimals in the asymptotic suction boundary layer: transition thresholds and symmetry breaking. Phys. Fluids 27 (3), 034108.CrossRefGoogle Scholar
Cherubini, S., De Palma, P., Robinet, J.-C.. & Bottaro, A. 2010 a Rapid path to transition via nonlinear localized optimal perturbations in a boundary-layer flow. Phys. Rev. E 82 (6), 066302.CrossRefGoogle Scholar
Cherubini, S., De Palma, P., Robinet, J.-C. & Bottaro, A. 2011 The minimal seed of turbulent transition in the boundary layer. J. Fluid Mech. 689, 221–253.CrossRefGoogle Scholar
Cherubini, S., Robinet, J.-C., Bottaro, A. & De Palma, P. 2010 b Optimal wave packets in a boundary layer and initial phases of a turbulent spot. J. Fluid Mech. 656, 231–259.CrossRefGoogle Scholar
Couliou, M. & Monchaux, R. 2015 Large-scale flows in transitional plane Couette flow: a key ingredient of the spot growth mechanism. Phys. Fluids 27 (3), 034101.CrossRefGoogle Scholar
Duguet, Y., Monokrousos, A., Brandt, L. & Henningson, D.S. 2013 Minimal transition thresholds in plane Couette flow. Phys. Fluids 25 (8), 084103.CrossRefGoogle Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar–turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110, 034502.CrossRefGoogle ScholarPubMed
Duguet, Y., Schlatter, P. & Henningson, D.S. 2010 Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 650, 119–129.CrossRefGoogle Scholar
Eckhardt, B., Schneider, T.M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.CrossRefGoogle Scholar
Emmons, H.W. 1951 The laminar–turbulent transition in a boundary layer – Part I. J. Aeronaut. Sci. 18 (7), 490–498.CrossRefGoogle Scholar
Farano, M., Cherubini, S., Robinet, J.-C. & De Palma, P. 2015 Hairpin-like optimal perturbations in plane Poiseuille flow. J. Fluid Mech. 775, R2.CrossRefGoogle Scholar
Farano, M., Cherubini, S., Robinet, J.-C. & De Palma, P. 2016 Subcritical transition scenarios via linear and nonlinear localized optimal perturbations in plane Poiseuille flow. Fluid Dyn. Res. 48 (6), 061409.CrossRefGoogle Scholar
Farano, M., Cherubini, S., Robinet, J.-C. & De Palma, P. 2017 Optimal bursts in turbulent channel flow. J. Fluid Mech. 817, 35–60.CrossRefGoogle Scholar
Foures, D.P.G., Caulfield, C.P. & Schmid, P.J. 2013 Localization of flow structures using $\infty$-norm optimization. J. Fluid Mech. 729, 672–701.CrossRefGoogle Scholar
Gibson, J.F., et al. 2021 Channelflow 2.0. channelflow.ch.Google Scholar
Gomé, S., Tuckerman, L.S. & Barkley, D. 2020 Statistical transition to turbulence in plane channel flow. Phys. Rev. Fluids 5, 083905.CrossRefGoogle Scholar
Griewank, A. & Walther, A. 2000 Algorithm 799: revolve: an implementation of checkpointing for the reverse or adjoint mode of computational differentiation. ACM Trans. Math. Softw. 26 (1), 19–45.CrossRefGoogle Scholar
Henningson, D.S. & Kim, J. 1991 On turbulent spots in plane Poiseuille flow. J. Fluid Mech. 228, 183–205.Google Scholar
Hinze, M., Walther, A. & Sternberg, J. 2006 An optimal memory-reduced procedure for calculating adjoints of the instationary Navier–Stokes equations. Opt. Control Applics. Meth. 27 (1), 19–40.CrossRefGoogle Scholar
Jiménez, J. 2013 How linear is wall-bounded turbulence? Phys. Fluids 25 (11), 110814.CrossRefGoogle Scholar
Kashyap, P.V., Duguet, Y. & Dauchot, O. 2020 Flow statistics in the transitional regime of plane channel flow. Entropy 22 (9), 1001.CrossRefGoogle ScholarPubMed
Kerswell, R.R. 2018 Nonlinear nonmodal stability theory. Annu. Rev. Fluid Mech. 50 (1), 319–345.CrossRefGoogle Scholar
Kerswell, R.R., Pringle, C.C.T. & Willis, A.P. 2014 An optimisation approach for analysing nonlinear stability with transition to turbulence in fluids as an exemplar . Rep. Prog. Phys. 77, 085901.CrossRefGoogle Scholar
Klingmann, B.G.B. 1992 On transition due to three-dimensional disturbances in plane Poiseuille flow. J. Fluid Mech. 240, 167–195.CrossRefGoogle Scholar
Klotz, L., Pavlenko, A.M. & Wesfreid, J.E. 2021 Experimental measurements in plane Couette–Poiseuille flow: dynamics of the large- and small-scale flow. J. Fluid Mech. 912, A24.CrossRefGoogle Scholar
Lagha, M. & Manneville, P. 2007 Modeling of plane Couette flow. I. Large scale flow around turbulent spots. Phys. Fluids 19 (9), 094105.CrossRefGoogle Scholar
Lemoult, G., Aider, J.-L. & Wesfreid, J.E. 2013 Turbulent spots in a channel: large-scale flow and self-sustainability. J. Fluid Mech. 731, R1.CrossRefGoogle Scholar
Lemoult, G., Gumowski, K., Aider, J.-L. & Wesfreid, J.E. 2014 Turbulent spots in channel flow: an experimental study. Eur. Phys. J. E 37 (4), 1–11.CrossRefGoogle ScholarPubMed
Lundbladh, A. & Johansson, A.V. 1991 Direct simulation of turbulent spots in plane Couette flow. J. Fluid Mech. 229, 499–516.CrossRefGoogle Scholar
Marensi, E., Willis, A.P. & Kerswell, R.R. 2019 Stabilisation and drag reduction of pipe flows by flattening the base profile. J. Fluid Mech. 863, 850–875.CrossRefGoogle Scholar
Marxen, O. & Zaki, T.A. 2019 Turbulence in intermittent transitional boundary layers and in turbulence spots. J. Fluid Mech. 860, 350–383.CrossRefGoogle Scholar
Monokrousos, A., Bottaro, A., Brandt, L., Di Vita, A. & Henningson, D.S. 2011 Nonequilibrium thermodynamics and the optimal path to turbulence in shear flows. Phys. Rev. Lett. 106 (13), 134502.CrossRefGoogle ScholarPubMed
Orr, W.M'F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part II: a viscous liquid. In Proceedings of the Royal Irish Academy. Section A: Mathematical and Physical Sciences, pp. 69–138. JSTOR.Google Scholar
Paranjape, C. 2019 Onset of turbulence in plane Poiseuille flow. PhD thesis, IST Austria.Google Scholar
Parente, E., Robinet, J.-C., De Palma, P. & Cherubini, S. 2021 Linear and nonlinear optimal growth mechanisms for generating turbulent bands. J. Fluid Mech. 938, A25.CrossRefGoogle Scholar
Prigent, A., Grégoire, G., Chaté, H., Dauchot, O. & van Saarloos, W. 2002 Large-scale finite-wavelength modulation within turbulent shear flows. Phys. Rev. Lett. 89 (1), 014501.CrossRefGoogle ScholarPubMed
Pringle, C.C.T. & Kerswell, R.R. 2010 Using nonlinear transient growth to construct the minimal seed for shear flow turbulence. Phys. Rev. Lett. 105 (15), 154502.CrossRefGoogle ScholarPubMed
Pringle, C.C.T., Willis, A.P. & Kerswell, R.R. 2012 Minimal seeds for shear flow turbulence: using nonlinear transient growth to touch the edge of chaos. J. Fluid Mech. 702, 415–443.CrossRefGoogle Scholar
Pringle, C.C.T., Willis, A.P. & Kerswell, R.R. 2015 Fully localised nonlinear energy growth optimals in pipe flow. Phys. Fluids 27 (6), 064102.CrossRefGoogle Scholar
Rabin, S.M.E., Caulfield, C.P. & Kerswell, R.R. 2012 Triggering turbulence efficiently in plane Couette flow. J. Fluid Mech. 712, 244–272.CrossRefGoogle Scholar
Rabin, S.M.E., Caulfield, C.P. & Kerswell, R.R. 2014 Designing a more nonlinearly stable laminar flow via boundary manipulation. J. Fluid Mech. 738, R1.CrossRefGoogle Scholar
Reynolds, O. 1883 III. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Proc. R. Soc. Lond. 35 (224–226), 84–99.Google Scholar
Schumacher, J. & Eckhardt, B. 2001 Evolution of turbulent spots in a parallel shear flow. Phys. Rev. E 63 (4), 046307.CrossRefGoogle Scholar
Shimizu, M. & Manneville, P. 2019 Bifurcations to turbulence in transitional channel flow. Phys. Rev. Fluids 4 (11), 113903.CrossRefGoogle Scholar
Song, B. & Xiao, X. 2020 Trigger turbulent bands directly at low Reynolds numbers in channel flow using a moving-force technique. J. Fluid Mech. 903, A43.CrossRefGoogle Scholar
Tao, J.J., Eckhardt, B. & Xiong, X.M. 2018 Extended localized structures and the onset of turbulence in channel flow. Phys. Rev. Fluids 3 (1), 011902.CrossRefGoogle Scholar
Tao, J. & Xiong, X. 2013 The unified transition stages in linearly stable shear flows. In Fourteenth Asia Congress of Fluid Mechanics, Hanoi and Halong, 15–19 October.Google Scholar
Tao, J. & Xiong, X. 2017 The unified transition stages in linearly stable shear flows. arXiv:1710.02258.Google Scholar
Tsukahara, T., Kawaguchi, Y. & Kawamura, H. 2014 An experimental study on turbulent-stripe structure in transitional channel flow. In Proceedings of the Sixth International Symposium on turbulence heat and mass transfer. Begell House.Google Scholar
Tsukahara, T., Seki, Y., Kawamura, H. & Tochio, D. 2005 DNS of turbulent channel flow at very low Reynolds numbers. In Fourth International Symposium on Turbulence and Shear Flow Phenomena. Begel House Inc.Google Scholar
Tuckerman, L.S. & Barkley, D. 2011 Patterns and dynamics in transitional plane Couette flow. Phys. Fluids 23 (4), 041301.CrossRefGoogle Scholar
Tuckerman, L.S., Chantry, M. & Barkley, D. 2020 Patterns in wall-bounded shear flows. Annu. Rev. Fluid Mech. 52, 343–367.CrossRefGoogle Scholar
Tuckerman, L.S., Kreilos, T., Schrobsdorff, H., Schneider, T.M. & Gibson, J.F. 2014 Turbulent–laminar patterns in plane Poiseuille flow. Phys. Fluids 26 (11), 114103.CrossRefGoogle Scholar
Vavaliaris, C., Beneitez, M. & Henningson, D.S. 2020 Optimal perturbations and transition energy thresholds in boundary layer shear flows. Phys. Rev. Fluids 5 (6), 062401.CrossRefGoogle Scholar
Wang, Z., Guet, C., Monchaux, R., Duguet, Y. & Eckhardt, B. 2020 Quadrupolar flows around spots in internal shear flows. J. Fluid Mech. 892, A27.CrossRefGoogle Scholar
Xiao, X. & Song, B. 2020 The growth mechanism of turbulent bands in channel flow at low Reynolds numbers. J. Fluid Mech. 883, R1.CrossRefGoogle Scholar
Xiong, X., Tao, J., Chen, S. & Brandt, L. 2015 Turbulent bands in plane-Poiseuille flow at moderate Reynolds numbers. Phys. Fluids 27 (4), 041702.CrossRefGoogle Scholar
Zuccher, S., Luchini, P. & Bottaro, A. 2004 Algebraic growth in a Blasius boundary layer: optimal and robust control by mean suction in the nonlinear regime. J. Fluid Mech. 513, 135–160.CrossRefGoogle Scholar