Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T14:29:57.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical simulations of Rayleigh–Bénard convection for Prandtl numbers between 10−1 and 104 and Rayleigh numbers between 105 and 109

Published online by Cambridge University Press:  14 September 2010

G. SILANO ,
K. R. SREENIVASAN  and
R. VERZICCO
G. SILANO
Affiliation:
Università degli Studi di Trieste, DMI, 34127 Trieste, Italy International Centre for Theoretical Physics, 34014 Trieste, Italy
K. R. SREENIVASAN
Affiliation:
International Centre for Theoretical Physics, 34014 Trieste, Italy Courant Institute of Mathematical Sciences and Department of Physics, New York University, NY 10012, USA
R. VERZICCO*
Affiliation:
Università di Roma ‘Tor Vergata’, DIM, 00133 Rome, Italy University of Twente, PoF, 7500 AE, Enschede, The Netherlands
*
†Email address for correspondence: verzicco@uniroma2.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We summarize the results of an extensive campaign of direct numerical simulations of Rayleigh–Bénard convection at moderate and high Prandtl numbers (10−1 ≤ Pr ≤ 104) and moderate Rayleigh numbers (105 ≤ Ra ≤ 109). The computational domain is a cylindrical cell of aspect ratio Γ = 1/2, with the no-slip condition imposed on all boundaries. By scaling the numerical results, we find that the free-fall velocity should be multiplied by 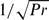in order to obtain a more appropriate representation of the large-scale velocity at high Pr. We investigate the Nusselt and the Reynolds number dependences on Ra and Pr, comparing the outcome with previous numerical and experimental results. Depending on Pr, we obtain different power laws of the Nusselt number with respect to Ra, ranging from Ra2/7 for Pr = 1 up to Ra0.31 for Pr = 103. The Nusselt number is independent of Pr. The Reynolds number scales as 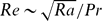, neglecting logarithmic corrections. We analyse the global and local features of viscous and thermal boundary layers and their scaling behaviours with respect to Ra and Pr, and with respect to the Reynolds and Péclet numbers. We find that the flow approaches a saturation state when Reynolds number decreases below the critical value, Res ≃ 40. The thermal-boundary-layer thickness increases slightly (instead of decreasing) when the Péclet number increases, because of the moderating influence of the viscous boundary layer. The simulated ranges of Ra and Pr contain steady, periodic and turbulent solutions. A rough estimate of the transition from the steady to the unsteady state is obtained by monitoring the time evolution of the system until it reaches stationary solutions. We find multiple solutions as long-term phenomena at Ra = 108 and Pr = 103, which, however, do not result in significantly different Nusselt numbers. One of these multiple solutions, even if stable over a long time interval, shows a break in the mid-plane symmetry of the temperature profile. We analyse the flow structures through the transitional phases by direct visualizations of the temperature and velocity fields. A wide variety of large-scale circulation and plume structures has been found. The single-roll circulation is characteristic only of the steady and periodic solutions. For other regimes at lower Pr, the mean flow generally consists of two opposite toroidal structures; at higher Pr, the flow is organized in the form of multi-jet structures, extending mostly in the vertical direction. At high Pr, plumes mainly detach from sheet-like structures. The signatures of different large-scale structures are generally well reflected in the data trends with respect to Ra, less in those with respect to Pr.

JFM classification

Turbulent Flows: Turbulent convection Boundary Layers: Boundary layer structure
Type
Papers
Information
Journal of Fluid Mechanics , Volume 662 , 10 November 2010 , pp. 409 - 446
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Ahlers, G. & Xu, X. 2001 Prandtl-number dependence of heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 86, 3320–3323.Google Scholar
Ashkenazi, S. & Steinberg, V. 1999 High Rayleigh number turbulent convection in a gas near the gas–liquid critical point. Phys. Rev. Lett. 83, 3641–3644.CrossRefGoogle Scholar
Batchelor, G. K. 1959 Small scale variation of convected quantities like temperature in turbulent fluid. J. Fluid Mech. 5, 113–133.CrossRefGoogle Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1993 Boundary layer length scales in thermal turbulence. Phys. Rev. Lett. 70, 4067.CrossRefGoogle ScholarPubMed
Bénard, H. 1900 Les tourbillons cellulaires dans une nappe liquide. Revue Gen. Sci. Pures Appl. 11, 1261–1271.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.CrossRefGoogle Scholar
Boronska, K. & Tuckerman, L. S. 2006 Standing and travelling waves in cylindrical Rayleigh–Bénard convection. J. Fluid Mech. 559, 279–298.CrossRefGoogle Scholar
Boronska, K. & Tuckerman, L. S. 2010 Extreme multiplicity in cylindrical Rayleigh–Bénard convection: I. time-dependence and oscillations. Phys. Rev. E 81, 036321.Google Scholar
Breuer, M., Wessling, S., Schmalzl, J. & Hansen, U. 2004 Effect of inertia in Rayleigh–Bénard convection. Phys. Rev. E 69, 026302.Google Scholar
Brown, E. & Ahlers, G. 2009 The origin of oscillations of the large-scale circulation of turbulent Rayleigh–Bénard convection. J. Fluid Mech. 638, 383–400.Google Scholar
Brown, E., Funfschilling, D. & Ahlers, G. 2007 Anomalous Reynolds-number scaling in turbulent Rayleigh–Bénard convection. J. Stat. Mech. P10005.Google Scholar
Calzavarini, E., Lohse, D., Toschi, F. & Tripiccione, R. 2005 Rayleigh and Prandtl number scaling in the bulk of Rayleigh–Bénard turbulence. Phys. Fluids 17, 055107.Google Scholar
Castaing, B., Guranatne, G., Heslot, F., Kadanoff, L., Libchaber, A. & Thomae, S. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.CrossRefGoogle Scholar
Chandrasekar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford Univ. Press.Google Scholar
Charlson, G. S. & Sani, R. L. 1970 Thermoconvective instability in a bounded cylindrical fluid layer. Intl J. Heat Mass Transfer 13, 1479–1496.CrossRefGoogle Scholar
Chavanne, X., Chilla, F., Castaing, B. & Hebral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300–1320.CrossRefGoogle Scholar
Clever, R. & Busse, F. 1974 Transition to time-dependent convection. J. Fluid Mech. 65, 625–645.Google Scholar
Croquette, V., Le Gal, P. & Pocheau, A. 1986 Spatial features of the transition to chaos in an extended system. Phys. Scripta T 13, 135.CrossRefGoogle Scholar
Daya, Z. A. & Ecke, R. E. 2001 Does turbulent convection feel the shape of the container? Phys. Rev. Lett. 87 (18), 184501.Google Scholar
Donzis, D. A., Sreenivasan, K. R. & Yeung, P. K. 2010 The Batchelor spectrum for mixing of passive scalars in isotropic turbulence. Flow, Turb. Combust. (in press).CrossRefGoogle Scholar
Emran, M. S. & Schumacher, J. 2008 Fine-scale statistics of temperature and its derivatives in convective turbulence. J. Fluid Mech. 611, 13–34.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle ScholarPubMed
Hardin, G. R. & Sani, R. L. 1993 Weakly non-linear solutions. Intl J. Numer. Meth. Fluids 17, 755.Google Scholar
Heslot, F., Castaing, B. & Libchaber, A. 1987 Transitions to turbulence in helium gas. Phys. Rev. A 36, 5870–5873.CrossRefGoogle ScholarPubMed
Hof, B., Lucas, G. J. & Mullin, T. 1999 Flow state multiplicity in convection. Phys. Fluids 11, 2815–2817.Google Scholar
Kerr, R. M. & Herring, J. R. 2000 Prandtl number dependence of Nusselt number in direct numerical simulations. J. Fluid Mech. 419, 325–344.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for a very large Reynolds numbers. Proc. R. Soc. Lond. A 434, 9–13.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5, 1374–1389.Google Scholar
Krishnamurti, R. & Howard, L. N. 1981 Large-scale flow generation in turbulent convection. Proc. Natl Acad. Sci. 78 (4), 1981–1985.Google Scholar
Lam, S., Shang, X., Zhou, S. & Xia, K. 2002 Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh–Bénard convection. Phys. Rev. Lett. E 65, 066306.CrossRefGoogle ScholarPubMed
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.CrossRefGoogle ScholarPubMed
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2001 The wind in confined thermal convection. J. Fluid Mech. 449, 169–178.CrossRefGoogle Scholar
Niemela, J. J. & Sreenivasan, K. R. 2003 Confined turbulent convection. J. Fluid Mech. 481, 355–384.CrossRefGoogle Scholar
Oresta, P., Stringano, G. & Verzicco, R. 2007 Transitional regimes and rotation effects in Rayleigh–Bénard convection in a slender cylindrical cell. Eur. J. Mech. B/Fluids 26 (1), 1–14.Google Scholar
Peltier, W. R. 1989 Mantle Convection: Plate Tectonics and Global Dynamics. Gordon and Breach.Google Scholar
Prandtl, L. 1952 Essentials of Fluid Mechanics, Chapter V. Hafner.Google Scholar
Rayleigh, Lord 1916 On convective currents in horizontal layer of fluid when the higher temperature is on the under side. Phil. Mag. 32, 529–546.CrossRefGoogle Scholar
Roche, P. E., Castaing, B., Chabaud, B. & Hébral, B. 2002 Prandtl and Rayleigh numbers dependencies in Rayleigh–Bénard convection. Europhys. Lett. 58, 693–698.Google Scholar
Rudiger, S. & Feudel, F. 2000 Patter formation in Rayleigh–Bénard convection in a cylindrical container. Phys. Rev. E 62, 4927–4931.CrossRefGoogle Scholar
Schmalzl, J., Breuer, M. & Hansen, U. 2002 The influence of the Prandtl number on the style of vigorous thermal convection. Goephys. Astrophys. Fluid Dyn. 96, 381–403.CrossRefGoogle Scholar
Schumacher, J., Sreenivasan, K. R. & Yeung, P. K. 2005 Very fine structures in scalar mixing. J. Fluid Mech. 531, 113–122.Google Scholar
Shishkina, O. & Thess, A. 2009 Mean temperature profiles in turbulent Rayleigh–Bénard convection of water. J. Fluid Mech. 633, 449–460.CrossRefGoogle Scholar
Shishkina, O. & Wagner, C. 2008 Analysis of sheet-like thermal plumes in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 599, 383–404.CrossRefGoogle Scholar
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh number convection. Phys. Rev. A 42, 3650–3653.CrossRefGoogle ScholarPubMed
Silano, G. 2009 Numerical simulations of thermal convection at high Prandtl numbers. PhD thesis, University of Trieste, http://hdl.handle.net/10077/3211.Google Scholar
Spalart, P. R. & Moser, R. D. 1991 Spectral methods for the Navier-Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96, 297–324.Google Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.CrossRefGoogle Scholar
Threlfall, D. C. 1975 Free convection in low-temperature gaseous helium. J. Fluid Mech. 67, 17–28.Google Scholar
Tritton, D. J. 1988 Physical Fluid Dynamics, 2nd edn. Clarendon Press.Google Scholar
Umemura, A. & Busse, F. H. 1989 Axisymmetric convection at large Rayleigh number and infinite Prandtl number. J. Fluid Mech. 208, 459–478.Google Scholar
Verzicco, R. 2003 Turbulent thermal convection in a closed domain: viscous boundary layer and mean flow effects. Eur. Phys. J. B 35, 133–141.CrossRefGoogle Scholar
Verzicco, R. & Camussi, R. 1997 Transitional regimes of low-Prandtl thermal convection in a cylindrical cell. Phys. Fluids 9, 1287–1295.CrossRefGoogle Scholar
Verzicco, R. & Camussi, R. 1999 Prandtl number effects in convective turbulence. J. Fluid Mech. 383, 55–73.Google Scholar
Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.CrossRefGoogle Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123, 402–414.Google Scholar
Xia, K., Liam, S. & Zhou, S. 2002 Heat-flux measurement in high-Prantdl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.Google Scholar
Zhou, Q. & Xia, K. Q. 2008 Comparative experimental study of local mixing of active and passive scalar in turbulent thermal convection. Phys. Rev. E 77, 056312.Google Scholar