Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-17T19:45:44.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillatory spontaneous dimpling in evaporating curved thin films

Published online by Cambridge University Press:  24 February 2020

Xingyi Shi Open the ORCID record for Xingyi Shi [Opens in a new window] ,
Gerald G. Fuller  and
Eric S. G. Shaqfeh
Xingyi Shi
Affiliation:
Department of Chemical Engineering, Stanford University, Stanford, CA94305, USA
Gerald G. Fuller
Affiliation:
Department of Chemical Engineering, Stanford University, Stanford, CA94305, USA
Eric S. G. Shaqfeh*
Affiliation:
Department of Chemical Engineering, Stanford University, Stanford, CA94305, USA Department of Mechanical Engineering, Stanford University, Stanford, CA94305, USA
*
†Email address for correspondence: esgs@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

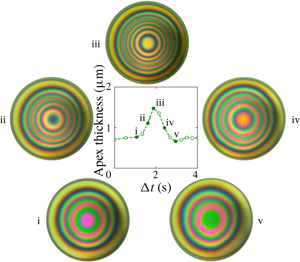
We examine the dynamics of a thin film composed of a non-evaporative silicone oil (high surface tension) with trace amounts of an evaporative silicone oil (low surface tension) over an air bubble. An evaporating thin liquid film is formed atop a capillary-pinned air bubble by squeezing then holding the bubble against the air–silicone oil interface. Despite the simplicity of the system, complex oscillatory dynamical behaviour has been observed. Through interferometric experiments and numerical simulations, we show that as the bubble is moved towards the opposite interface, a dimple forms and during the subsequent holding period the dimple spontaneously oscillates. The evaporation-driven solutal–thermal Marangoni flow thickens the film and capillarity subsequently discharges the dimple. Solutal and thermal Marangoni flows both contribute to film thickening and as the local concentration of the non-evaporative species increases, the strength of the Marangoni flows increases. The oscillation frequency and waveform depend on initial composition and the maximum dimple volume. We suggest that these oscillatory solutions and the associated mechanism are a partial explanation for the film stabilization in multicomponent oils, reported experimentally in a recent publication (Chandran Suja et al., Proc. Natl Acad. Sci., vol. 115, 2018, pp. 7919–7924).

JFM classification

Convection: Marangoni convection Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 889 , 25 April 2020 , A25
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allan, R. S., Charles, G. E. & Mason, S. G. 1961 The approach of gas bubbles to a gas/liquid interface. J. Colloid Sci. 16 (2), 150–165.Google Scholar
Bron, A. J., Tiffany, J. M., Gouveia, S. M., Yokoi, N. & Voon, L. W. 2004 Functional aspects of the tear film lipid layer. Exp. Eye Res. 78 (3), 347–360.Google ScholarPubMed
Cascao Pereira, L. G., Johansson, C., Blanch, H. W. & Radke, C. J. 2001 A bike-wheel microcell for measurement of thin-film forces. Colloids Surf. A 186 (1-2), 103–111.CrossRefGoogle Scholar
Chan, D. Y. C., Klaseboer, E. & Manica, R. 2011 Film drainage and coalescence between deformable drops and bubbles. Soft Matt. 7 (6), 2235–2264.CrossRefGoogle Scholar
Chandran Suja, V., Kar, A., Cates, W., Remmert, S. M., Savage, P. D. & Fuller, G. G. 2018 Evaporation-induced foam stabilization in lubricating oils. Proc. Natl Acad. Sci. 115 (31), 7919–7924.CrossRefGoogle ScholarPubMed
Chen, Y. J., Sadakane, K., Sakuta, H., Yao, C. & Yoshikawa, K. 2017 Spontaneous oscillations and synchronization of active droplets on a water surface via Marangoni convection. Langmuir 33 (43), 12362–12368.CrossRefGoogle ScholarPubMed
Chickos, J. S. & Acree, W. E. Jr. 2003 Enthalpies of vaporization of organic and organometallic compounds, 1880–2002. J. Phys. Chem. Ref. Data 32 (2), 519–878.CrossRefGoogle Scholar
Danov, K. D., Gurkov, T. D., Dimitrova, T., Ivanov, I. B. & Smith, D. 1997 Hydrodynamic theory for spontaneously growing dimple in emulsion films with surfactant mass transfer. J. Colloid Interface Sci. 188 (2), 313–324.CrossRefGoogle Scholar
Debrégeas, G. D., De Gennes, P.-G. & Brochard-Wyart, F. 1998 The life and death of ‘bare’ viscous bubbles. Science 279 (5357), 1704–1707.Google Scholar
Fournier, J. B. & Cazabat, A. M. 1992 Tears of wine. Europhys. Lett. 20 (6), 517–522.CrossRefGoogle Scholar
Frostad, J. M., Tammaro, D., Santollani, L., Bochner de Araujo, S. & Fuller, G. G. 2016 Dynamic fluid-film interferometry as a predictor of bulk foam properties. Soft Matt. 12 (46), 9266–9279.CrossRefGoogle ScholarPubMed
Guennebaud, G., Jacob, B. & Nuentsa-Wakam, D.2010 Eigen v3. Available at: http://eigen.tuxfamily.org.Google Scholar
Howell, P. D. 1999 The draining of a two-dimensional bubble. J. Engng Maths 35 (3), 251–272.CrossRefGoogle Scholar
Joye, J. L., Hirasaki, G. J. & Miller, C. A. 1992 Dimple formation and behavior during axisymmetrical foam film drainage. Langmuir 8 (12), 3083–3092.CrossRefGoogle Scholar
Klaseboer, E., Chevaillier, J. P., Gourdon, C. & Masbernat, O. 2000 Film drainage between colliding drops at constant approach velocity: experiments and modeling. J. Colloid Interface Sci. 229 (1), 274–285.CrossRefGoogle ScholarPubMed
Kočárková, H., Rouyer, F. & Pigeonneau, F. 2013 Film drainage of viscous liquid on top of bare bubble: influence of the bond number. Phys. Fluids 25 (2), 022105.CrossRefGoogle Scholar
Kovalchuk, N. M. & Vollhardt, D. 2002 Autooscillations of surface tension in water–alcohol systems. J. Phys. Chem. B 104 (33), 7987–7992.CrossRefGoogle Scholar
Kovalchuk, N. M. & Vollhardt, D. 2008 Oscillation of interfacial tension produced by transfer of nonionic surfactant through the liquid/liquid interface. J. Phys. Chem. C 112 (24), 9016–9022.CrossRefGoogle Scholar
Kovalchuk, V. I., Kamusewitz, H., Vollhardt, D. & Kovalchuk, N. M. 1999 Auto-oscillation of surface tension. Phys. Rev. E 60 (2), 2029–2036.CrossRefGoogle ScholarPubMed
Lechner, M. D., Wohlfarth, C. & Wohlfarth, B. 2015 Surface Tension of Pure Liquids and Binary Liquid Mixtures. Springer.Google Scholar
Overdiep, W. S. 1986 The levelling of paints. Prog. Org. Coat. 14, 159–175.CrossRefGoogle Scholar
Rodríguez-Hakim, M., Barakat, J. M., Shi, X., Shaqfeh, E. S. G. & Fuller, G. G. 2019 Evaporation-driven solutocapillary flow of thin liquid films over curved substrates. Phys. Rev. Fluids 4 (3), 1–22.CrossRefGoogle Scholar
Schwarzenberger, K., Aland, S., Domnick, H., Odenbach, S. & Eckert, K. 2015 Relaxation oscillations of solutal Marangoni convection at curved interfaces. Colloids Surf. A 481, 633–643.CrossRefGoogle Scholar
Stocker, R. & Bush, J. W. 2007 Spontaneous oscillations of a sessile lens. J. Fluid Mech. 583, 465–475.CrossRefGoogle Scholar
Velev, O. D., Gurkov, T. D. & Borwankar, R. P. 1993 Spontaneous cyclic dimpling in emulsion films due to surfactant mass transfer between the phases. J. Colloid Interface Sci. 159 (2), 497–501.CrossRefGoogle Scholar
Venerus, D. C. & Simavilla, D. N. 2015 Tears of wine: new insights on an old phenomenon. Sci. Rep. 5, 1–10.Google ScholarPubMed
Walls, D. J., Meiburg, E. & Fuller, G. G. 2018 The shape evolution of liquid droplets in miscible environments. J. Fluid Mech. 852, 422–452.CrossRefGoogle Scholar
Yañez-Soto, B., Mannis, M. J., Schwab, I. R., Li, J. Y., Leonard, B. C., Abbott, N. L. & Murphy, C. J. 2014 Interfacial phenomena and the ocular surface. Ocular Surf. 12 (3), 178–201.CrossRefGoogle ScholarPubMed
Yiantsios, S. G. & Davis, R. H. 1990 On the buoyancy-driven motion of a drop towards a rigid surface or a deformable interface. J. Fluid Mech. 217 (1990), 547–573.CrossRefGoogle Scholar
Yiantsios, S. G., Serpetsi, S. K., Doumenc, F. & Guerrier, B. 2015 Surface deformation and film corrugation during drying of polymer solutions induced by Marangoni phenomena. Intl J. Heat Mass Transfer 89, 1083–1094.CrossRefGoogle Scholar