Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mathai, Varghese
Zhu, Xiaojue
Sun, Chao
and
Lohse, Detlef
2018.
Flutter to tumble transition of buoyant spheres triggered by rotational inertia changes.
Nature Communications,
Vol. 9,
Issue. 1,
Castagna, Marco
Mazellier, Nicolas
and
Kourta, Azeddine
2018.
Wake of super-hydrophobic falling spheres: influence of the air layer deformation.
Journal of Fluid Mechanics,
Vol. 850,
Issue. ,
p.
646.
Zhang, Jie
Mercier, Matthieu J.
and
Magnaudet, Jacques
2019.
Core mechanisms of drag enhancement on bodies settling in a stratified fluid.
Journal of Fluid Mechanics,
Vol. 875,
Issue. ,
p.
622.
Toupoint, Clément
Ern, Patricia
and
Roig, Véronique
2019.
Kinematics and wake of freely falling cylinders at moderate Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 866,
Issue. ,
p.
82.
Rivero-Rodriguez, Javier
and
Scheid, Benoit
2019.
Mass transfer around bubbles flowing in cylindrical microchannels.
Journal of Fluid Mechanics,
Vol. 869,
Issue. ,
p.
110.
Seyed-Ahmadi, Arman
and
Wachs, Anthony
2019.
Dynamics and wakes of freely settling and rising cubes.
Physical Review Fluids,
Vol. 4,
Issue. 7,
Bintein, Pierre-Brice
Bense, Hadrien
Clanet, Christophe
and
Quéré, David
2019.
Self-propelling droplets on fibres subject to a crosswind.
Nature Physics,
Vol. 15,
Issue. 10,
p.
1027.
Mathai, Varghese
Lohse, Detlef
and
Sun, Chao
2020.
Bubbly and Buoyant Particle–Laden Turbulent Flows.
Annual Review of Condensed Matter Physics,
Vol. 11,
Issue. 1,
p.
529.
Mandel, Tracy L.
Zhou, De Zhen
Waldrop, Lindsay
Theillard, Maxime
Kleckner, Dustin
and
Khatri, Shilpa
2020.
Retention of rising droplets in density stratification.
Physical Review Fluids,
Vol. 5,
Issue. 12,
Ershkov, Sergey V.
Christianto, Victor
Shamin, Roman V.
and
Giniyatullin, Ayrat R.
2020.
About analytical ansatz to the solving procedure for Kelvin–Kirchhoff equations.
European Journal of Mechanics - B/Fluids,
Vol. 79,
Issue. ,
p.
87.
Shi, Pengyu
Rzehak, Roland
Lucas, Dirk
and
Magnaudet, Jacques
2020.
Hydrodynamic forces on a clean spherical bubble translating in a wall-bounded linear shear flow.
Physical Review Fluids,
Vol. 5,
Issue. 7,
Ershkov, Sergey V.
Leshchenko, Dmytro
and
Giniyatullin, Ayrat R.
2020.
Solving procedure for the Kelvin–Kirchhoff equations in case of buoyant (or the falling) ellipsoid of rotation.
European Journal of Mechanics - B/Fluids,
Vol. 81,
Issue. ,
p.
23.
Kramer, Onno J. I.
de Moel, Peter J.
Raaghav, Shravan K. R.
Baars, Eric T.
van Vugt, Wim H.
Breugem, Wim-Paul
Padding, Johan T.
and
van der Hoek, Jan Peter
2021.
Can terminal settling velocity and drag of natural particles in water ever be predicted accurately?.
Drinking Water Engineering and Science,
Vol. 14,
Issue. 1,
p.
53.
Werner, Lukas
Rettinger, Christoph
and
Rüde, Ulrich
2021.
Coupling fully resolved light particles with the lattice Boltzmann method on adaptively refined grids.
International Journal for Numerical Methods in Fluids,
Vol. 93,
Issue. 11,
p.
3280.
Hu, Shi-Yuan
Wang, Kai-Zhe
Jia, Lai-Bing
Zhong, Jin-Qiang
and
Zhang, Jun
2021.
Enhanced heat transport in thermal convection with suspensions of rod-like expandable particles.
Journal of Fluid Mechanics,
Vol. 928,
Issue. ,
Kharrouba, Mohammed
Pierson, Jean-Lou
and
Magnaudet, Jacques
2021.
Flow structure and loads over inclined cylindrical rodlike particles and fibers.
Physical Review Fluids,
Vol. 6,
Issue. 4,
Will, Jelle B.
and
Krug, Dominik
2021.
Dynamics of freely rising spheres: the effect of moment of inertia.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Romanus, Rodrigo S.
Lugarini, Alan
and
Franco, Admilson T.
2021.
An immersed boundary-lattice Boltzmann framework for fully resolved simulations of non-spherical particle settling in unbounded domain.
Computers & Mathematics with Applications,
Vol. 102,
Issue. ,
p.
206.
Raaghav, Shravan K.R.
Poelma, Christian
and
Breugem, Wim-Paul
2021.
Path Instabilities of a Freely Rising or Falling Sphere.
SSRN Electronic Journal ,
Will, Jelle B.
Mathai, Varghese
Huisman, Sander G.
Lohse, Detlef
Sun, Chao
and
Krug, Dominik
2021.
Kinematics and dynamics of freely rising spheroids at high Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 912,
Issue. ,
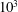 $10^{3}$
is set up by varying independently the body-to-fluid density ratio and the relative magnitude of inertial and viscous effects in approximately 250 distinct combinations. These computations confirm or reveal the presence of several distinct periodic regions on the route to chaos, most of which only exist within a finite range of the sphere relative density and Reynolds number. The wake structure is analysed in these various regimes, evidencing the existence of markedly different shedding modes according to the style of path. The variation of the drag force with the flow parameters is also examined, revealing that only one of the styles of path specific to very light spheres yields a non-standard drag behaviour, with drag coefficients significantly larger than those measured on a fixed sphere under equivalent conditions. The outcomes of this investigation are compared with available experimental and numerical results, evidencing points of consensus and disagreement.
$10^{3}$
is set up by varying independently the body-to-fluid density ratio and the relative magnitude of inertial and viscous effects in approximately 250 distinct combinations. These computations confirm or reveal the presence of several distinct periodic regions on the route to chaos, most of which only exist within a finite range of the sphere relative density and Reynolds number. The wake structure is analysed in these various regimes, evidencing the existence of markedly different shedding modes according to the style of path. The variation of the drag force with the flow parameters is also examined, revealing that only one of the styles of path specific to very light spheres yields a non-standard drag behaviour, with drag coefficients significantly larger than those measured on a fixed sphere under equivalent conditions. The outcomes of this investigation are compared with available experimental and numerical results, evidencing points of consensus and disagreement.



