Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-30T20:24:30.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Propagating and evanescent internal waves in a deep ocean model

Published online by Cambridge University Press:  13 July 2012

M. S. Paoletti  and
Harry L. Swinney
M. S. Paoletti*
Affiliation:
Department of Physics and Center for Nonlinear Dynamics, University of Texas at Austin, Austin, TX 78712, USA
Harry L. Swinney
Affiliation:
Department of Physics and Center for Nonlinear Dynamics, University of Texas at Austin, Austin, TX 78712, USA
*
†Email address for correspondence: mpaoletti@chaos.utexas.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

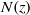We present experimental and computational studies of the propagation of internal waves in a stratified fluid with an exponential density profile that models the deep ocean. The buoyancy frequency profile (proportional to the square root of the density gradient) varies smoothly by more than an order of magnitude over the fluid depth, as is common in the deep ocean. The non-uniform stratification is characterized by a turning depth 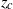, where 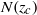is equal to the wave frequency 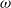and . 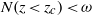Internal waves reflect from the turning depth and become evanescent below the turning depth. The energy flux below the turning depth is shown to decay exponentially with a decay constant given by 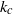, which is the horizontal wavenumber at the turning depth. The viscous decay of the vertical velocity amplitude of the incoming and reflected waves above the turning depth agree within a few per cent with a previously untested theory for a fluid of arbitrary stratification (Kistovich and Chashechkin, J. Appl. Mech. Tech. Phys., vol. 39, 1998, pp. 729–737).

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Ocean processes Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 571 - 583
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Fincham, A. & Delerce, G. 2000 Advanced optimization of correlation imaging velocimetry algorithms. Exp. Fluids 29, 13–22.Google Scholar
2. Gostiaux, L., Dauxois, T., Didelle, H., Sommeria, J. & Viboud, S. 2006 Quantitative laboratory observations of internal wave reflection on ascending slopes. Phys. Fluids 18, 056602.CrossRefGoogle Scholar
3. Gostiaux, L., Didelle, H., Mercier, S. & Dauxois, T. 2007 A novel internal waves generator. Exp. Fluids 42, 123–130.CrossRefGoogle Scholar
4. Gregory, K. D. & Sutherland, B. R. 2010 Transmission and reflection of internal wave beams. Phys. Fluids 22, 106601.Google Scholar
5. Ham, F. & Iaccarino, G. 2004 Energy conservation in collocated discretization schemes on unstructured meshes. In Annual Research Briefs, pp. 3–14. Center for Turbulence Research.Google Scholar
6. Ham, F., Mattsson, K. & Iaccarino, G. 2006 Accurate and stable finite volume operators for unstructured flow solvers. In Annual Research Briefs, pp. 243–261. Center for Turbulence Research.Google Scholar
7. Hill, D. F. 2002 General density gradients in general domains: the two-tank method revisited. Exp. Fluids 32, 434–440.CrossRefGoogle Scholar
8. Javam, A., Imberger, J. & Armfield, S. W. 1999 Numerical study of internal wave reflection from sloping boundaries. J. Fluid Mech. 396, 183–201.CrossRefGoogle Scholar
9. King, B., Stone, M., Zhang, H. P., Gerkema, T., Marder, M., Scott, R. B. & Swinney, H. L. 2012 Buoyancy frequency profiles and internal semidiurnal tide turning depths in the oceans. J. Geophys. Res. (Oceans) 117, 4008.CrossRefGoogle Scholar
10. Kistovich, Y. V. & Chashechkin, Y. D. 1998 Linear theory of the propagation of internal wave beams in an arbitrarily stratified liquid. J. Appl. Mech. Tech. Phys. 39, 729–737.CrossRefGoogle Scholar
11. Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197, 215–240.CrossRefGoogle Scholar
12. Mathur, M. & Peacock, T. 2009 Internal wave beam propagation in non-uniform stratifications. J. Fluid Mech. 639, 133–152.CrossRefGoogle Scholar
13. Mathur, M. & Peacock, T. 2010 Internal wave interferometry. Phys. Rev. Lett. 104, 118501.CrossRefGoogle ScholarPubMed
14. Munk, W. & Wunsch, C. 1998 Abyssal recipes. Part 1. Energetics of tidal and wind mixing. Deep-Sea Res. I 45, 1977–2010.CrossRefGoogle Scholar
15. Nault, J. T. & Sutherland, B. R. 2007 Internal wave transmission in non-uniform flows. Phys. Fluids 19 (1), 016601.CrossRefGoogle Scholar
16. Pingree, R. D. & New, A. L. 1991 Abyssal penetration and bottom reflection of internal tidal energy in the Bay of Biscay. J. Phys. Oceanogr. 21, 28–39.Google Scholar
17. Rodenborn, B., Kiefer, D., Zhang, H. P. & Swinney, H. L. 2011 Harmonic generation by reflecting internal waves. Phys. Fluids 23, 026601.CrossRefGoogle Scholar
18. Slinn, D. N. & Riley, J. J. 1998 A model for the simulation of turbulent boundary layers in an incompressible stratified flow. J. Comput. Phys. 144, 550–602.Google Scholar
19. Sutherland, B. R. & Yewchuk, K. 2004 Internal wave tunnelling. J. Fluid Mech. 511, 125–134.Google Scholar
20. Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36, 281–314.Google Scholar
Supplementary material: PDF

Paoletti and Swinney supplementary material

Supplementary tables

Download Paoletti and Swinney supplementary material(PDF)
PDF 145.5 KB