Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T17:08:20.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-similar spectra of point-source scalar plumes in a turbulent boundary layer

Published online by Cambridge University Press:  14 May 2019

K. M. Talluru Open the ORCID record for K. M. Talluru [Opens in a new window] ,
Jimmy Philip  and
K. A. Chauhan
K. M. Talluru*
Affiliation:
School of Civil Engineering, The University of Sydney, New South Wales 2006, Australia
Jimmy Philip
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
K. A. Chauhan
Affiliation:
School of Civil Engineering, The University of Sydney, New South Wales 2006, Australia
*
†Email address for correspondence: murali.talluru@sydney.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Measurements of concentration fluctuations in a passive scalar plume released within a turbulent boundary layer are utilised to ascertain the scaling of concentration spectra. It is observed that the concentration spectra in a narrow meandering plume has a self-similar behaviour in both transverse (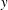$y$) and vertical ($z$, i.e. wall-normal) directions. Experimental data reveal self-similarity when the magnitude of concentration spectra is scaled by the local concentration variance whereas frequency is suitably scaled utilising the integral length scale of the streamwise velocity or the boundary layer thickness and the source velocity as length and velocity scales, respectively. Furthermore, our data show that at each frequency, the concentration energy is distributed across the 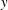$y$ and $z$ directions that is proportional to concentration variance at that location. These results are consistent with our non-dimensional analysis. Based on these observations, if the mean plume statistics are known, a model is proposed with which concentration spectrum at any position within the plume can be calculated using the spectrum at any another location as the input. The model is tested extensively for point-source plumes released at various heights and streamwise distances in a turbulent boundary layer, and is found to predict spectra at different $y$ and $z$ locations in close agreement with measurements.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , pp. 698 - 717
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J. P. & Marusic, I. 2017 Distance-from-the-wall scaling of turbulent motions in wall-bounded flows. Phys. Fluids 29 (2), 020712.Google Scholar
Becker, H. A., Hottel, H. C. & Williams, G. C. 1967 The nozzle-fluid concentration field of the round, turbulent, free jet. J. Fluid Mech. 30 (2), 285–303.Google Scholar
Birch, A. D., Brown, D. R., Dodson, M. G. & Thomas, J. R. 1978 The turbulent concentration field of a methane jet. J. Fluid Mech. 88 (3), 431–449.Google Scholar
Cassiani, M., Franzese, P. & Giostra, U. 2005 A PDF micromixing model of dispersion for atmospheric flow. Part II. Application to convective boundary layer. Atmos. Environ. 39 (8), 1471–1479.Google Scholar
Chatwin, P. C. & Sullivan, P. J. 1990 A simple and unifying physical interpretation of scalar fluctuation measurements from many turbulent shear flows. J. Fluid Mech. 212, 533–556.Google Scholar
Chauhan, K. A., Nagib, H. M. & Monkewitz, P. A. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.Google Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22 (4), 469–473.Google Scholar
Djenidi, L. & Antonia, R. A. 2012 A spectral chart method for estimating the mean turbulent kinetic energy dissipation rate. Exp. Fluids 53 (4), 1005–1013.Google Scholar
Fackrell, J. E. 1980 A flame ionisation detector for measuring fluctuating concentration. J. Phys. E: Sci. Instrum. 13 (8), 888–893.Google Scholar
Fackrell, J. E. & Robins, A. G. 1982a Concentration fluctuations and fluxes in plumes from point sources in a turbulent boundary layer. J. Fluid Mech. 117, 1–26.Google Scholar
Fackrell, J. E. & Robins, A. G. 1982b The effects of source size on concentration fluctuations in plumes. Boundary-Layer Meteorol. 22 (3), 335–350.Google Scholar
Gifford, F. 1959 Statistical properties of a fluctuating plume dispersion model. Adv. Geophys. 6, 117–137.Google Scholar
Hanna, S. R. 1986 Spectra of concentration fluctuations: the two time scales of a meandering plume. Atmos. Environ. 20 (6), 1131–1137.Google Scholar
Hanna, S. R. & Insley, E. M. 1989 Time series analyses of concentration and wind fluctuations. Boundary-Layer Meteorol. 47 (1–4), 131–147.Google Scholar
Hinze, J. O. 1975 Turbulence. McGraw-Hill.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Marro, M., Salizzoni, P., Soulhac, L. & Cassiani, M. 2018 Dispersion of a passive scalar fluctuating plume in a turbulent boundary layer. Part III. Stochastic modelling. Boundary-Layer Meteorol. 167 (3), 349–369.Google Scholar
Morrill, W. C., Philip, J. & Klewicki, J. 2017 An invariant representation of mean inertia: theoretical basis for a log law in turbulent boundary layers. J. Fluid Mech. 813, 594–617.Google Scholar
Mylne, K. R., Davidson, M. J. & Thomson, D. J. 1996 Concentration fluctuation measurements in tracer plumes using high and low frequency response detectors. Boundary-Layer Meteorol. 79 (3), 225–242.Google Scholar
Nironi, C., Salizzoni, P., Marro, M., Mejean, P., Grosjean, N. & Soulhac, L. 2015 Dispersion of a passive scalar fluctuating plume in a turbulent boundary layer. Part I. Velocity and concentration measurements. Boundary-Layer Meteorol. 156 (3), 415–446.Google Scholar
Obukhov, A. M. 1949 The local structure of atmospheric turbulence. In Dokl. Akad. Nauk. SSSR, vol. 67, pp. 643–646.Google Scholar
Panofsky, H. A. & Dutton, J. A. 1984 Atmospheric Turbulence: Models and Methods for Engineering Applications. John Wiley.Google Scholar
Pitts, W. M. & Kashiwagi, T. 1984 The application of laser-induced Rayleigh light scattering to the study of turbulent mixing. J. Fluid Mech. 141, 391–429.Google Scholar
Pope, S. B. 2001 Turbulent Flows. Cambridge University Press.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
Sawford, B. L., Frost, C. C. & Allan, T. C. 1985 Atmospheric boundary-layer measurements of concentration statistics from isolated and multiple sources. Boundary-Layer Meteorol. 31 (3), 249–268.Google Scholar
Sawford, B. L. & Sullivan, P. J. 1995 A simple representation of a developing contaminant concentration field. J. Fluid Mech. 289, 141–157.Google Scholar
Schlichting, H. 1979 Boundary-Layer Theory. McGraw-Hill.Google Scholar
Shraiman, B. I. & Siggia, E. D. 2000 Scalar turbulence. Nature 405 (6787), 639.Google Scholar
Sreenivasan, K. R. 1996 The passive scalar spectrum and the obukhov–corrsin constant. Phys. Fluids 8 (1), 189–196.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.Google Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.Google Scholar
Talluru, K. M., Hernandez-Silva, C. & Chauhan, K. A. 2019 A robust calibration technique for concentration measurements using ionisation detectors. Meas. Sci. Tech., https://doi.org/10.1088/1361-6501/ab0c5b.Google Scholar
Talluru, K. M., Hernandez-Silva, C., Philip, J. & Chauhan, K. A. 2017a Measurements of scalar released from point sources in a turbulent boundary layer. Meas. Sci. Tech. 28 (5), 055801.Google Scholar
Talluru, K. M., Hernandez-Silva, C., Philip, J. & Chauhan, K. A.2017b Measurements of velocity and concentration in a high Reynolds number turbulent boundary layer. In 10th International Symposium on Turbulence and Shear Flow Phenomena, Chicago, USA, Begel House Inc.Google Scholar
Talluru, K. M., Philip, J. & Chauhan, K. A. 2018 Local transport of passive scalar released from a point source in a turbulent boundary layer. J. Fluid Mech. 846, 292–317.Google Scholar
Taylor, G. I. 1922 Diffusion by continuous movements. Proc. Lond. Math. Soc. 2 (1), 196–212.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Vanderwel, C. & Tavoularis, S. 2014 Measurements of turbulent diffusion in uniformly sheared flow. J. Fluid Mech. 754, 488–514.Google Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32 (1), 203–240.Google Scholar
Weil, J. C. 2012 Atmospheric dispersion. In Handbook of Environmental Fluid Dynamics, Volume Two: Systems, Pollution Modeling and Measurements (ed. Fernando, H. J.), pp. 163–174. CRC Press.Google Scholar
Yee, E., Wang, B. C. & Lien, F. S. 2009 Probabilistic model for concentration fluctuations in compact-source plumes in an urban environment. Boundary-Layer Meteorol. 130 (2), 169–208.Google Scholar