Hostname: page-component-5db58dd55d-htx7c Total loading time: 0 Render date: 2026-06-14T08:34:05.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-similarity of the large-scale motions in turbulent pipe flow

Published online by Cambridge University Press:  02 March 2016

Leo H. O. Hellström ,
Ivan Marusic  and
Alexander J. Smits
Leo H. O. Hellström*
Affiliation:
Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Ivan Marusic
Affiliation:
Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
Alexander J. Smits
Affiliation:
Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: lhellstr@Princeton.EDU
Get access Rights & Permissions [Opens in a new window]

Abstract

Townsend’s attached eddy hypothesis assumes the existence of a set of energetic and geometrically self-similar eddies in the logarithmic layer in wall-bounded turbulent flows, which can be scaled with their distance to the wall. To examine the possible self-similarity of the energetic eddies in fully developed turbulent pipe flow, we performed stereo particle image velocimetry measurements together with a proper orthogonal decomposition analysis. 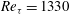For two Reynolds numbers, $Re_{{\it\tau}}=1330$ and 2460, the resulting modes/eddies were shown to exhibit self-similar behaviour for eddies with wall-normal length scales spanning a decade. This single length scale provides a complete description of the cross-sectional shape of the self-similar eddies.

JFM classification

Boundary Layers: Boundary layer structure Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulence modelling

Information

Type
Rapids
Information
Journal of Fluid Mechanics , Volume 792 , 10 April 2016 , R1
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Bailey, S. C. C. & Smits, A. J. 2010 Experimental investigation of the structure of large- and very large-scale motions in turbulent pipe flow. J. Fluid Mech. 651, 339–356.CrossRefGoogle Scholar
Baltzer, J. R., Adrian, R. J. & Wu, X. 2013 Structural organization of large and very large scales in turbulent pipe flow simulation. J. Fluid Mech. 720, 236–279.Google Scholar
Chung, D., Marusic, I., Monty, J. P., Vallikivi, M. & Smits, A. J. 2015 On the universality of inertial energy in the log layer of turbulent boundary layer and pipe flows. Exp. Fluids 56 (7), 1–10.CrossRefGoogle Scholar
Glauser, M. N. & George, W. K. 1987 Orthogonal decomposition of the axisymmetric jet mixing layer including azimuthal dependence. In Advances in Turbulence, pp. 357–366. Springer.CrossRefGoogle Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Hellström, L. H. O., Ganapathisubramani, B. & Smits, A. J. 2015 The evolution of large-scale motions in turbulent pipe flow. J. Fluid Mech. 779, 701–715.CrossRefGoogle Scholar
Hellström, L. H. O., Sinha, A. & Smits, A. J. 2011 Visualizing the very-large-scale motions in turbulent pipe flow. Phys. Fluids 23, 011703.CrossRefGoogle Scholar
Hellström, L. H. O. & Smits, A. J. 2014 The energetic motions in turbulent pipe flow. Phys. Fluids 26 (12), 125102.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 094501.CrossRefGoogle ScholarPubMed
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.Google Scholar
Jimenez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (04), 741–773.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to $Re_{{\it\tau}}=5200$ . J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation, pp. 166–178. Nauka.Google Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13 (3), 735–743.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Woodcock, J. D. & Marusic, I. 2015 The statistical behaviour of attached eddies. Phys. Fluids 27 (1), 015104.Google Scholar