Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-19T01:13:27.247Z Has data issue: false hasContentIssue false
  • English
  • Français

Shear reversal in dense suspensions: the challenge to fabric evolution models from simulation data

Published online by Cambridge University Press:  29 May 2018

Rahul N. Chacko Open the ORCID record for Rahul N. Chacko [Opens in a new window] ,
Romain Mari ,
Suzanne M. Fielding  and
Michael E. Cates Open the ORCID record for Michael E. Cates [Opens in a new window]
Rahul N. Chacko*
Affiliation:
Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
Romain Mari
Affiliation:
DAMTP, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Suzanne M. Fielding
Affiliation:
Department of Physics, Durham University, South Road, Durham DH1 3LE, UK
Michael E. Cates
Affiliation:
DAMTP, Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: r.n.chacko@durham.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Dense suspensions of hard particles are important as industrial or environmental materials (e.g. fresh concrete, food, paint or mud). To date, most constitutive models developed to describe them are, explicitly or effectively, ‘fabric evolution models’ based on: (i) a stress rule connecting the macroscopic stress to a second-rank microstructural fabric tensor 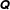$\unicode[STIX]{x1D64C}$; and (ii) a closed time-evolution equation for 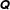$\unicode[STIX]{x1D64C}$. In dense suspensions, most of the stress comes from short-ranged pairwise steric or lubrication interactions at near-contacts (suitably defined), so a natural choice for $\unicode[STIX]{x1D64C}$ is the deviatoric second moment of the distribution 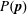$P(\boldsymbol{p})$ of the near-contact orientations 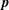$\boldsymbol{p}$. Here we test directly whether a closed time-evolution equation for such a 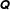$\unicode[STIX]{x1D64C}$ can exist, for the case of inertialess non-Brownian hard spheres in a Newtonian solvent. We perform extensive numerical simulations accessing high levels of detail for the evolution of 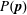$P(\boldsymbol{p})$ under shear reversal, providing a stringent test for fabric evolution models. We consider a generic class of these models as defined by Hand (J. Fluid Mech., vol. 13, 1962, pp. 33–46) that assumes little as to the micromechanical behaviour of the suspension and is only constrained by frame indifference. Motivated by the smallness of microstructural anisotropies in the dense regime, we start with linear models in this class and successively consider those increasingly nonlinear in 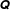$\unicode[STIX]{x1D64C}$. Based on these results, we suggest that no closed fabric evolution model properly describes the dynamics of the fabric tensor under reversal. We attribute this to the fact that, while a second-rank tensor captures reasonably well the microstructure in steady flows, it gives a poor description during significant parts of the microstructural evolution following shear reversal. Specifically, the truncation of 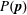$P(\boldsymbol{p})$ at second spherical harmonic (or second-rank tensor) level describes ellipsoidal distributions of near-contact orientations, whereas on reversal we observe distributions that are markedly four-lobed; moreover, ${\dot{P}}(\boldsymbol{p})$ has oblique axes, not collinear with those of 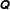$\unicode[STIX]{x1D64C}$ in the shear plane. This structure probably precludes any adequate closure at second-rank level. Instead, our numerical data suggest that closures involving the coupled evolution of both a fabric tensor and a fourth-rank tensor might be reasonably accurate.

JFM classification

Non-Newtonian Flows: Rheology Low-Reynolds-number flows: Stokesian dynamics Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 847 , 25 July 2018 , pp. 700 - 734
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ball, R. C. & Melrose, J. R. 1997 A simulation technique for many spheres in quasi-static motion under frame-invariant pair drag and Brownian forces. Physica A 247, 444–472.CrossRefGoogle Scholar
Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.Google Scholar
Batchelor, G. K. & Green, J. T. 1972 The determination of the bulk stress in a suspension of spherical particles to order c 2 . J. Fluid Mech. 56, 401–427.Google Scholar
Bingham, C. 1974 An antipodally symmetric distribution on the sphere. Ann. Stat. 2, 1201–1225.Google Scholar
Blanc, F., Lemaire, E., Meunier, A. & Peters, F. 2013 Microstructure in sheared non-Brownian concentrated suspensions. J. Rheol. 57, 273–292.Google Scholar
Blanc, F., Lemaire, E. & Peters, F. 2014 Tunable fall velocity of a dense ball in oscillatory cross-sheared concentrated suspensions. J. Fluid Mech. 746, R4.Google Scholar
Blanc, F., Peters, F. & Lemaire, E. 2011a Experimental signature of the pair trajectories of rough spheres in the shear-induced microstructure in noncolloidal suspensions. Phys. Rev. Lett. 107, 208302.Google Scholar
Blanc, F., Peters, F. & Lemaire, E. 2011b Local transient rheological behavior of concentrated suspensions. J. Rheol. 55, 835–854.CrossRefGoogle Scholar
Boyer, F., Guazzelli, É. & Pouliquen, O. 2011a Unifying suspension and granular rheology. Phys. Rev. Lett. 107, 188301.CrossRefGoogle ScholarPubMed
Boyer, F., Pouliquen, O. & Guazzelli, É. 2011b Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.CrossRefGoogle Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.CrossRefGoogle Scholar
Brown, E. & Jaeger, H. M. 2009 Dynamic jamming point for shear thickening suspensions. Phys. Rev. Lett. 103, 086001.Google Scholar
Brown, E. & Jaeger, H. M. 2012 The role of dilation and confining stresses in shear thickening of dense suspensions. J. Rheol. 56, 875–923.Google Scholar
Castle, J., Farid, A. & Woodcock, L. V. 1996 The effect of surface friction on the rheology of hard-sphere colloids. Prog. Colloid Polym. Sci. 100, 259–265.CrossRefGoogle Scholar
Chaubal, C. V. & Leal, L. G. 1998 A closure approximation for liquid-crystalline polymer models based on parametric density estimation. J. Rheol. 42, 177–201.CrossRefGoogle Scholar
Cheng, J., Jia, X. Z. & Wang, Y. B. 2007 Numerical differentiation and its applications. Inverse Probl. Sci. Eng. 15, 339–357.CrossRefGoogle Scholar
Cheng, X., McCoy, J. H., Israelachvili, J. N. & Cohen, I. 2011 Imaging the microscopic structure of shear thinning and thickening colloidal suspensions. Science 333, 1276–1279.CrossRefGoogle ScholarPubMed
Clavaud, C., Bérut, A., Metzger, B. & Forterre, Y. 2017 Revealing the frictional transition in shear-thickening suspensions. Proc. Natl Acad. Sci. USA 114, 5147–5152.CrossRefGoogle ScholarPubMed
Comtet, J., Chatté, G., Niguès, A., Bocquet, L., Siria, A. & Colin, A. 2017 Pairwise frictional profile between particles determines discontinuous shear thickening transition in non-colloidal suspensions. Nat. Commun. 8, 15633.CrossRefGoogle ScholarPubMed
Couturier, É., Boyer, F., Pouliquen, O. & Guazzelli, É. 2011 Suspensions in a tilted trough: second normal stress difference. J. Fluid Mech. 686, 26–39.Google Scholar
Cundall, P. A. & Strack, O. D. L. 1979 A discrete numerical model for granular assemblies. Géotechnique 29, 47–65.Google Scholar
Dai, S.-C., Bertevas, E., Qi, F. & Tanner, R. I. 2013 Viscometric functions for noncolloidal sphere suspensions with Newtonian matrices. J. Rheol. 57, 493–510.Google Scholar
Dbouk, T., Lobry, L. & Lemaire, E. 2013 Normal stresses in concentrated non-Brownian suspensions. J. Fluid Mech. 715, 239–272.Google Scholar
Denn, M. M. & Morris, J. F. 2014 Rheology of non-Brownian suspensions. Annu. Rev. Chem. Biomol. Eng. 5, 203–228.CrossRefGoogle ScholarPubMed
Fernandez, N., Mani, R., Rinaldi, D., Kadau, D., Mosquet, M., Lombois-Burger, H., Cayer-Barrioz, J., Herrmann, H. J., Spencer, N. D. & Isa, L. 2013 Microscopic mechanism for shear thickening of non-Brownian suspensions. Phys. Rev. Lett. 111, 108301.Google Scholar
Frankel, N. A. & Acrivos, A. 1967 On the viscosity of a concentrated suspension of solid spheres. Chem. Engng Sci. 22, 847–853.Google Scholar
Gadala-Maria, F. & Acrivos, A. 1980 Shear-induced structure in a concentrated suspension of solid spheres. J. Rheol. 24, 799–814.CrossRefGoogle Scholar
Gallier, S., Lemaire, E., Peters, F. & Lobry, L. 2014 Rheology of sheared suspensions of rough frictional particles. J. Fluid Mech. 757, 514–549.CrossRefGoogle Scholar
Giesekus, H. 1982 A simple constitutive equation for polymer fluids based on the concept of deformation-dependent tensorial mobility. J. Non-Newtonian Fluid Mech. 11, 69–109.Google Scholar
Goddard, J. D. 2006 A dissipative anisotropic fluid model for non-colloidal particle dispersions. J. Fluid Mech. 568, 1–17.Google Scholar
Goddard, J. D. 2008 A weakly nonlocal anisotropic fluid model for inhomogeneous Stokesian suspensions. Phys. Fluids 20, 040601.CrossRefGoogle Scholar
Goddard, J. D. 2014 Continuum modeling of granular media. Appl. Mech. Rev. 66, 050801.Google Scholar
Gurnon, A. K. & Wagner, N. J. 2015 Microstructure and rheology relationships for shear thickening colloidal dispersions. J. Fluid Mech. 769, 242–276.CrossRefGoogle Scholar
Guy, B. M., Hermes, M. & Poon, W. C. K. 2015 Towards a unified description of the rheology of hard-particle suspensions. Phys. Rev. Lett. 115, 088304.CrossRefGoogle ScholarPubMed
Hand, G. L. 1962 A theory of anisotropic fluids. J. Fluid Mech. 13, 33–46.CrossRefGoogle Scholar
Hinch, E. J. & Leal, L. G. 1975 Constitutive equations in suspension mechanics. Part 1. General formulation. J. Fluid Mech. 71, 481–495.CrossRefGoogle Scholar
Hinch, E. J. & Leal, L. G. 1976 Constitutive equations in suspension mechanics. Part 2. Approximate forms for a suspension of rigid particles affected by Brownian rotations. J. Fluid Mech. 76, 187–208.Google Scholar
Hwang, W. R. & Hulsen, M. A. 2006 Direct numerical simulations of hard particle suspensions in planar elongational flow. J. Non-Newtonian Fluid Mech. 136, 167–178.CrossRefGoogle Scholar
Jeffrey, D. J. 1992 The calculation of the low Reynolds number resistance functions for two unequal spheres. Phys. Fluids A 4, 16–29.CrossRefGoogle Scholar
Jeffrey, D. J. & Onishi, Y. 1984 Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 139, 261–290.Google Scholar
Johnson, M. W. & Segalman, D. 1977 A model for viscoelastic fluid behavior which allows non-affine deformation. J. Non-Newtonian Fluid Mech. 2, 255–270.Google Scholar
Kanatani, K.-I. 1984 Distribution of directional data and fabric tensors. Int. J. Eng. Sci. 22, 149–164.Google Scholar
Kolli, V. G., Pollauf, E. J. & Gadala-Maria, F. 2002 Transient normal stress response in a concentrated suspension of spherical particles. J. Rheol. 46, 321–334.Google Scholar
Kraynik, A. M. & Reinelt, D. A. 1992 Extensional motions of spatially periodic lattices. Intl J. Multiphase Flow 18, 1045–1059.CrossRefGoogle Scholar
Kuzuu, N. & Doi, M. 1983 Constitutive equation for nematic liquid crystals under weak velocity gradient derived from a molecular kinetic equation. J. Phys. Soc. Japan 52, 3486–3494.Google Scholar
Larson, R. G. 2013 Constitutive Equations for Polymer Melts and Solutions, Butterworths Series in Chemical Engineering. Butterworth-Heinemann.Google Scholar
Lees, A. W. & Edwards, S. F. 1972 The computer study of transport processes under extreme conditions. J. Phys. C Solid State Phys. 5, 1921–1928.Google Scholar
Lin, N. Y. C., Guy, B. M., Hermes, M., Ness, C., Sun, J., Poon, W. C. K. & Cohen, I. 2015 Hydrodynamic and contact contributions to continuous shear thickening in colloidal suspensions. Phys. Rev. Lett. 115, 228304.Google Scholar
Lin, N. Y. C., Ness, C., Cates, M. E., Sun, J. & Cohen, I. 2016 Tunable shear thickening in suspensions. Proc. Natl Acad. Sci. USA 113, 10774–10778.Google Scholar
Lootens, D., Van Damme, H., Hémar, Y. & Hébraud, P. 2005 Dilatant flow of concentrated suspensions of rough particles. Phys. Rev. Lett. 95, 268302.Google Scholar
Luding, S. 2008 Cohesive, frictional powders: contact models for tension. Granul. Matt. 10, 235–246.Google Scholar
Magnanimo, V. & Luding, S. 2011 A local constitutive model with anisotropy for ratcheting under 2D axial-symmetric isobaric deformation. Granul. Matt. 13, 225–232.Google Scholar
Mari, R., Seto, R., Morris, J. F. & Denn, M. M. 2014 Shear thickening, frictionless and frictional rheologies. J. Rheol. 58, 1693–1724.Google Scholar
Mari, R., Seto, R., Morris, J. F. & Denn, M. M. 2015 Discontinuous shear thickening in Brownian suspensions by dynamic simulation. Proc. Natl Acad. Sci. USA 112, 15326–15330.CrossRefGoogle ScholarPubMed
Morris, J. F. & Katyal, B. 2002 Microstructure from simulated Brownian suspension flows at large shear rate. Phys. Fluids 14, 1920–1937.CrossRefGoogle Scholar
Narumi, T., See, H., Honma, Y., Hasegawa, T., Takahashi, T. & Phan-Thien, N. 2002 Transient response of concentrated suspensions after shear reversal. J. Rheol. 46, 295–305.Google Scholar
Nazockdast, E. & Morris, J. F. 2012 Microstructural theory and the rheology of concentrated colloidal suspensions. J. Fluid Mech. 713, 420–452.CrossRefGoogle Scholar
Nazockdast, E. & Morris, J. F. 2013 Pair-particle dynamics and microstructure in sheared colloidal suspensions: simulation and Smoluchowski theory. Phys. Fluids 25, 070601.Google Scholar
Ness, C. & Sun, J. 2016 Two-scale evolution during shear reversal in dense suspensions. Phys. Rev. E 93, 012604.Google ScholarPubMed
Noll, W.1955 On the continuity of the solid and fluid states. PhD thesis, Indiana University.Google Scholar
Peters, F., Ghigliotti, G., Gallier, S., Blanc, F., Lemaire, E. & Lobry, L. 2016a Rheology of non-Brownian suspensions of rough frictional particles under shear reversal: a numerical study. J. Rheol. 60, 715–732.Google Scholar
Peters, I. R., Majumdar, S. & Jaeger, H. M. 2016b Direct observation of dynamic shear jamming in dense suspensions. Nature 532, 214–217.CrossRefGoogle ScholarPubMed
Phan-Thien, N. 1995 Constitutive equation for concentrated suspensions in Newtonian liquids. J. Rheol. 39, 679–695.Google Scholar
Phan-Thien, N., Fan, X.-J. & Khoo, B. C. 1999 A new constitutive model for monodispersed suspensions of spheres at high concentrations. Rheol. Acta 38, 297–304.Google Scholar
Qi, L. 2006 Rank and eigenvalues of a supersymmetric tensor, the multivariate homogeneous polynomial and the algebraic hypersurface it defines. J. Symb. Comput. 41, 1309–1327.Google Scholar
Rivlin, R. 1955 Further remarks on the stress-deformation relations for isotropic materials. Indiana Univ. Math. J. 4, 681–702.Google Scholar
Seto, R., Giusteri, G. G. & Martiniello, A. 2017 Microstructure and thickening of dense suspensions under extensional and shear flows. J. Fluid Mech. 825, R3.Google Scholar
Seto, R., Mari, R., Morris, J. F. & Denn, M. M. 2013 Discontinuous shear thickening of frictional hard-sphere suspensions. Phys. Rev. Lett. 111, 218301.CrossRefGoogle ScholarPubMed
Singh, A. & Nott, P. R. 2003 Experimental measurements of the normal stresses in sheared Stokesian suspensions. J. Fluid Mech. 490, 293–320.Google Scholar
Stickel, J. J., Phillips, R. J. & Powell, R. L. 2006 A constitutive model for microstructure and total stress in particulate suspensions. J. Rheol. 50, 379–413.CrossRefGoogle Scholar
Sun, J. & Sundaresan, S. 2011 A constitutive model with microstructure evolution for flow of rate-independent granular materials. J. Fluid Mech. 682, 590–616.CrossRefGoogle Scholar
Wagner, N. J. & Ackerson, B. J. 1992 Analysis of nonequilibrium structures of shearing colloidal suspensions. J. Chem. Phys. 97, 1473–1483.CrossRefGoogle Scholar
Zarraga, I. E., Hill, D. A. & Leighton, D. T. 2000 The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 44, 185–220.Google Scholar