Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-18T23:18:58.839Z Has data issue: false hasContentIssue false
  • English
  • Français

The spontaneous generation of inertia–gravity waves during frontogenesis forced by large strain: numerical solutions

Published online by Cambridge University Press:  07 May 2015

Callum J. Shakespeare  and
J. R. Taylor
Callum J. Shakespeare
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
J. R. Taylor*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: J.R.Taylor@damtp.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

A fully nonlinear numerical model is used to investigate spontaneous wave generation during two-dimensional frontogenesis forced by a horizontal strain field. The model uses the idealised configuration of an infinitely long straight front and uniform potential vorticity, with a uniform imposed convergent strain across the front. Shakespeare & Taylor (J. Fluid Mech., vol. 757, 2014, pp. 817–853) formulated a generalised analytical model (ST14) for this system that extends the classical Hoskins & Bretherton (J. Atmos. Sci., vol. 29, 1972, pp. 11–37) model (HB) to large strain rates (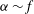${\it\alpha}\sim f$). Here, we use a numerical model to simulate the fully nonlinear problem and compare the results with the predictions of the analytical model for a variety of strain rates. Even for weak strains (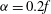${\it\alpha}=0.2f$), the confinement of the secondary circulation and the spontaneous generation of waves, predicted by ST14, are shown to be important corrections to the HB solution. These inviscid predictions are also robust for an equilibrated front where strain-forced frontogenesis is balanced by diffusion. For strong strains the wavefield becomes of leading-order importance to the solution. In this case the frontal circulation is tightly confined, and the vertical velocity is an order of magnitude larger than in the HB model. The addition of a strain field that weakens with time allows the release and propagation of the spontaneously generated waves. We also consider fronts with both large vorticity and strain rate, beyond the validity of the ST14 model.

JFM classification

Geophysical and Geological Flows: Ocean circulation Geophysical and Geological Flows: Ocean processes Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 772 , 10 June 2015 , pp. 508 - 534
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alford, M. H., Shcherbina, A. Y. & Gregg, M. C. 2013 Observations of near-inertial internal gravity waves radiating from a frontal jet. J. Phys. Oceanogr. 43, 1225–1239.Google Scholar
Blumen, W. 2000 Inertial oscillations and frontogenesis in a zero potential vorticity model. J. Phys. Oceanogr. 30, 31–39.2.0.CO;2>CrossRefGoogle Scholar
Chavanne, C., Flament, P. & Gurgel, K. W. 2010 Intereactions between a submesoscale anticyclonic vortex and a front. J. Phys. Oceanogr. 40, 1802–1818.Google Scholar
Gall, R., Williams, R. & Clark, T. 1987 On the minimum scale of surface fronts. J. Atmos. Sci. 44, 2562–2574.2.0.CO;2>CrossRefGoogle Scholar
Garner, S. T. 1989 Fully Lagrangian numerical solutions of unbalanced frontogensis and frontal collapse. J. Atmos. Sci. 46, 717–739.2.0.CO;2>CrossRefGoogle Scholar
Hoskins, B. J. 1982 The mathematical theory of frontogenesis. Annu. Rev. Fluid Mech. 14, 131–151.CrossRefGoogle Scholar
Hoskins, B. J. & Bretherton, F. P. 1972 Atmospheric frontogenesis models: mathematical formulation and solution. J. Atmos. Sci. 29, 11–37.Google Scholar
Levy, M., Ferrari, R., Franks, P. J. S., Martin, A. P. & Riviere, P. 2012 Bringing physics to life at the submesoscale. Geophys. Res. Lett. 39, L14602.Google Scholar
Mahadevan, A. & Tandon, A. 2006 An analysis of the mechanisms for submesoscale vertical motion at ocean fronts. Ocean Model. 14, 241–256.CrossRefGoogle Scholar
Plougonven, R. & Zhang, F. 2007 On the forcing of inertia–gravity waves by synoptic-scale flows. J. Atmos. Sci. 64, 1737–1742.Google Scholar
Plougonven, R. & Zhang, F. 2014 Internal gravity waves from atmospheric jets and fronts. Rev. Geophys. 52 (1), 33–76.Google Scholar
Shakespeare, C. J. & Taylor, J. R. 2013 A generalized mathematical model of geostrophic adjustment and frontogenesis: uniform potential vorticity. J. Fluid Mech. 736, 366–413.Google Scholar
Shakespeare, C. J. & Taylor, J. R. 2014 The spontaneous generation of inertia–gravity waves during frontogenesis forced by large strain: theory. J. Fluid Mech. 757, 817–853.Google Scholar
Shcherbina, A. Y., D’Asaro, E. A., Lee, C. M., Klymak, J. M., Molemaker, M. J. & McWilliams, J. C. 2013 Statistics of vertical vorticity, divergence, and strain in a developed submesoscale turbulence field. Geophys. Res. Lett. 40, 4706–4711.Google Scholar
Snyder, C., Skamarock, W. & Rotunno, R. 1993 Frontal dynamics near and following frontal collapse. J. Atmos. Sci. 50, 3194–3211.2.0.CO;2>CrossRefGoogle Scholar
Taylor, J. R.2008 Numerical simulations of the stratified oceanic bottom boundary layer. PhD thesis, University of California, San Diego.Google Scholar
Thomas, L. N., Tandon, A. & Mahadevan, A. 2008 Submesoscale processes and dynamics. In Ocean Modeling in an Eddying Regime, Geophysical Monograph Series, vol. 177. American Geophysical Union.Google Scholar
Vanneste, J. 2013 Balance and spontaneous wave generation in geophysical flows. Annu. Rev. Fluid Mech. 45, 147–172.CrossRefGoogle Scholar
Vanneste, J. & Yavneh, I. 2004 Exponentially small inertia–gravity waves and the breakdown of quasigeostrophic balance. J. Atmos. Sci. 61 (2), 211–223.Google Scholar
Viudez, A. 2007 The origin of the stationary frontal wave packet spontaneously generated in rotating stratified vortex dipoles. J. Fluid Mech. 593, 359–383.CrossRefGoogle Scholar
Viudez, A. & Dritschel, D. G. 2006 Spontaneous generation of inertia–gravity wave packets by balanced geophysical flows. J. Fluid Mech. 553, 107–117.Google Scholar