Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T19:04:26.175Z Has data issue: false hasContentIssue false
  • English
  • Français

Subcritical versus supercritical transition to turbulence in curved pipes

Published online by Cambridge University Press:  08 April 2015

J. Kühnen ,
P. Braunshier ,
M. Schwegel ,
H. C. Kuhlmann  and
B. Hof
J. Kühnen*
Affiliation:
IST Austria, Am Campus 1, A-3400 Klosterneuburg, Austria
P. Braunshier
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, Vienna University of Technology, Getreidemarkt 9, A-1060 Vienna, Austria
M. Schwegel
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, Vienna University of Technology, Getreidemarkt 9, A-1060 Vienna, Austria
H. C. Kuhlmann
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, Vienna University of Technology, Getreidemarkt 9, A-1060 Vienna, Austria
B. Hof
Affiliation:
IST Austria, Am Campus 1, A-3400 Klosterneuburg, Austria
*
†Email address for correspondence: jakob.kuehnen@ist.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

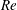Transition to turbulence in straight pipes occurs in spite of the linear stability of the laminar Hagen–Poiseuille flow if both the amplitude of flow perturbations and the Reynolds number $\mathit{Re}$ exceed a minimum threshold (subcritical transition). As the pipe curvature increases, centrifugal effects become important, modifying the basic flow as well as the most unstable linear modes. If the curvature (tube-to-coiling diameter 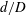$d/D$) is sufficiently large, a Hopf bifurcation (supercritical instability) is encountered before turbulence can be excited (subcritical instability). We trace the instability thresholds in the 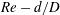$\mathit{Re}-d/D$ parameter space in the range 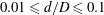$0.01\leqslant d/D\leqslant 0.1$ by means of laser-Doppler velocimetry and determine the point where the subcritical and supercritical instabilities meet. Two different experimental set-ups are used: a closed system where the pipe forms an axisymmetric torus and an open system employing a helical pipe. Implications for the measurement of friction factors in curved pipes are discussed.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Instability: Instability Instability: Transition to turbulence
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 770 , 10 May 2015 , R3
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D.  & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333 (6039), 192–196.Google Scholar
Cioncolini, A. & Santini, L. 2006 An experimental investigation regarding the laminar to turbulent flow transition in helically coiled pipes. Exp. Therm. Fluid Sci. 30 (4), 367–380.CrossRefGoogle Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulent transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.Google Scholar
Germano, M. 1982 On the effect of torsion in helical pipe flow. J. Fluid Mech. 125, 1–8.CrossRefGoogle Scholar
Grossmann, S. 2000 The onset of shear flow turbulence. Rev. Mod. Phys. 72, 603.Google Scholar
Hof, B., Westerweel, J., Schneider, T. M. & Eckhardt, B. 2006 Finite lifetime of turbulence in shear flows. Nature 443, 59.CrossRefGoogle ScholarPubMed
Hüttl, T. J. & Friedrich, R. 2000 Influence of curvature and torsion on turbulent flow in helically coiled pipes. Int. J. Heat Fluid Flow 21, 345–353.Google Scholar
Ito, H. 1959 Friction factors for turbulent flow in curved pipes. Trans. ASME J. Basic Engng 81, 123–134.Google Scholar
Kubair, V. & Varrier, C. B. S. 1961 Pressure drop for liquid flow in helical coils. Trans. Indian Inst. Chem. Engng 14, 93.Google Scholar
Kühnen, J., Holzner, M., Hof, B. & Kuhlmann, H. C. 2014 Experimental investigation of transitional flow in a toroidal pipe. J. Fluid Mech. 738, 463–491.Google Scholar
Kuik, D. J., Poelma, C. & Westerweel, J. 2010 Quantitative measurement of the lifetime of localized turbulence in pipe flow. J. Fluid Mech. 645, 529–539.Google Scholar
Mullin, T. 2011 Experimental studies of transition to turbulence in a pipe. Annu. Rev. Fluid Mech. 43 (1), 1–24.CrossRefGoogle Scholar
Naphon, P. & Wongwises, S. 2006 A review of flow and heat transfer characteristics in curved tubes. Renew. Sustainable Energy Rev. 10, 463–490.CrossRefGoogle Scholar
Nishi, M., Unsal, B., Durst, F. & Biswas, G. 2008 Laminar-to-turbulent transition of pipe flows through puffs and slugs. J. Fluid Mech. 614, 425.Google Scholar
Noorani, A., Khoury, G. K. El & Schlatter, P. 2013 Evolution of turbulence characteristics from straight to curved pipes. Intl J. Heat Fluid Flow 41 (0), 16–26.Google Scholar
Piazza, I. D. & Ciofalo, M. 2011 Transition to turbulence in toroidal pipes. J. Fluid Mech. 687, 72–117.Google Scholar
Samanta, D., de Lozar, A. & Hof, B. 2011 Experimental investigation of laminar turbulent intermittency in pipe flow. J. Fluid Mech. 681, 193–204.Google Scholar
Sreenivasan, K. R. & Strykowski, P. J. 1983 Stabilization effects in flow through helically coiled pipes. Exp. Fluids 1, 31–36.Google Scholar
Vashisth, S., Kumar, V. & Nigam, K. D. P. 2008 A review on the potential applications of curved geometries in process industry. Ind. Engng Chem. Res. 47 (10), 3291–3337.Google Scholar
Webster, D. R. & Humphrey, J. A. C. 1993 Experimental observation of flow instability in a helical coil. Trans. ASME J. Fluids Engng 115 (3), 436–443.CrossRefGoogle Scholar
Webster, D. R. & Humphrey, J. A. C. 1997 Traveling wave instability in helical coil flow. Phys. Fluids 9, 407–418.Google Scholar
Wygnanski, I. J. & Champagne, F. H. 1973 On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 59, 281–335.Google Scholar
Yamamoto, K., Yanase, S. & Yoshida, T. 1994 Torsion effect on the flow in a helical pipe. Fluid Dyn. Res. 14, 259.CrossRefGoogle Scholar