Article contents
Turbulent bubble fountains
Published online by Cambridge University Press: 11 December 2017
Abstract
We explore the dynamics of turbulent bubble fountains produced when a descending stream of fresh water and air bubbles issues from a nozzle submerged in a tank of water. The bubbles have diameters of 2 to 5 mm and the fountains have source Froude numbers ranging from 10 to 240. The Reynolds numbers of the bubbly fountains range from 4000 to 24 000. The bubbles, carried into the tank by the downward jet of water, lead to a buoyancy force which reduces the downward momentum of the jet, thus producing a fountain. We find that 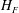 $H_{F}$, the downward penetration distance of the bubbles into the water reservoir, may be characterised by two parameters:
$H_{F}$, the downward penetration distance of the bubbles into the water reservoir, may be characterised by two parameters: 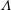 $\unicode[STIX]{x1D6EC}$, the ratio of the bubble rise speed to the characteristic fountain velocity,
$\unicode[STIX]{x1D6EC}$, the ratio of the bubble rise speed to the characteristic fountain velocity, 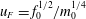 $u_{F}=f_{0}^{1/2}/m_{0}^{1/4}$, and
$u_{F}=f_{0}^{1/2}/m_{0}^{1/4}$, and 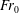 $Fr_{0}$, the source Froude number, given by
$Fr_{0}$, the source Froude number, given by 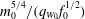 $m_{0}^{5/4}/(q_{W_{0}}f_{0}^{1/2})$, where
$m_{0}^{5/4}/(q_{W_{0}}f_{0}^{1/2})$, where 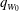 $q_{W_{0}}$,
$q_{W_{0}}$, 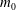 $m_{0}$ and
$m_{0}$ and 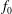 $f_{0}$ are the source volume, momentum and buoyancy fluxes. As
$f_{0}$ are the source volume, momentum and buoyancy fluxes. As 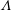 $\unicode[STIX]{x1D6EC}$ increases,
$\unicode[STIX]{x1D6EC}$ increases, 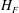 $H_{F}$ decreases, a result which is directly analogous to the height of rise of particles in a particle-laden fountain (Mingotti & Woods, J. Fluid Mech., vol. 793, 2016, R1). Also, we find that
$H_{F}$ decreases, a result which is directly analogous to the height of rise of particles in a particle-laden fountain (Mingotti & Woods, J. Fluid Mech., vol. 793, 2016, R1). Also, we find that 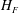 $H_{F}$ increases as
$H_{F}$ increases as 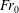 $Fr_{0}$ increases, a result directly analogous to single-phase fountains (Turner, J. Fluid Mech., vol. 26, 1966, pp. 779–792). We present a model for the conservation of volume, momentum and buoyancy fluxes and use this to predict the penetration distance of the bubbles corresponding to that point at which the fountain liquid velocity equals the bubble rise speed. Using the best-fit value for the entrainment coefficient,
$Fr_{0}$ increases, a result directly analogous to single-phase fountains (Turner, J. Fluid Mech., vol. 26, 1966, pp. 779–792). We present a model for the conservation of volume, momentum and buoyancy fluxes and use this to predict the penetration distance of the bubbles corresponding to that point at which the fountain liquid velocity equals the bubble rise speed. Using the best-fit value for the entrainment coefficient, 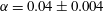 $\unicode[STIX]{x1D6FC}=0.04\pm 0.004$, we find that our experimental measurements of the bubble penetration distance are in good accord with the model predictions for
$\unicode[STIX]{x1D6FC}=0.04\pm 0.004$, we find that our experimental measurements of the bubble penetration distance are in good accord with the model predictions for 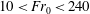 $10<Fr_{0}<240$ and
$10<Fr_{0}<240$ and 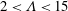 $2<\unicode[STIX]{x1D6EC}<15$. In our experiments the bubble rise speed,
$2<\unicode[STIX]{x1D6EC}<15$. In our experiments the bubble rise speed, 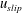 $u_{slip}$, is large compared to the entrainment velocity of the descending fountain. Thus, only a small fraction of the rising bubbles are re-entrained, and so the buoyancy flux of the fountain is approximately independent of depth. Flow-visualisation experiments also show that the liquid momentum flux is not exhausted at the point of bubble separation and so the liquid in the fountain continues to travel downward, separated from the bubbles. We use the new theoretical model to estimate the flux of air entrained into plunging water jets.
$u_{slip}$, is large compared to the entrainment velocity of the descending fountain. Thus, only a small fraction of the rising bubbles are re-entrained, and so the buoyancy flux of the fountain is approximately independent of depth. Flow-visualisation experiments also show that the liquid momentum flux is not exhausted at the point of bubble separation and so the liquid in the fountain continues to travel downward, separated from the bubbles. We use the new theoretical model to estimate the flux of air entrained into plunging water jets.
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 4
- Cited by



