Hostname: page-component-84b7d79bbc-c654p Total loading time: 0 Render date: 2024-07-28T17:15:09.612Z Has data issue: false hasContentIssue false
  • English
  • Français

‘Unforced’ Navier–Stokes solutions derived from convection in a curved channel

Published online by Cambridge University Press:  11 June 2018

R. H. Vaz Open the ORCID record for R. H. Vaz [Opens in a new window] ,
F. A. T. Boshier  and
A. J. Mestel Open the ORCID record for A. J. Mestel [Opens in a new window]
R. H. Vaz*
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
F. A. T. Boshier
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
A. J. Mestel
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: r.vaz14@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Steady Boussinesq flow in a weakly curved channel driven by a horizontal temperature gradient is considered. Linear variation in the transverse direction is assumed so that the problem reduces to a system of ordinary differential equations. A series expansion in 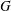$G$, a parameter proportional to the Grashof number and the square root of the curvature, reveals a real singularity and anticipates hysteresis. Numerical solutions are found using path continuation and the bifurcation diagrams for different parameter values are obtained. Multivalued solutions are observed as 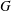$G$ and the Prandtl number vary. Often fields with the imposed structure that satisfy all the governing equations are insensitive to the boundary conditions and can be regarded as perturbations of the homogeneous (or ‘unforced’) problem. Four such unforced solutions are found. In two of these the velocity remains coupled with temperature which, formally, scales as 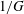$1/G$ as 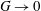$G\rightarrow 0$. The other two are purely hydrodynamic. The existence of such solutions is due to the unbounded nature of the domain. It is shown that these occur not only for the Dean equations, but constitute previously unreported solutions of the full Navier–Stokes equations in an annulus of arbitrary curvature. Two additional unforced solutions are found for large curvature.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Convection: Convection Mathematical Foundations: General fluid mechanics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 676 - 695
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agrawal, H. L. 1957 A new exact solution of the equations of viscous motion with axial symmetry. Q. J. Mech. Appl. Maths 10 (1), 42–44.Google Scholar
Allgower, E. L. & Georg, K. 1993 Continuation and path following. Acta Numer. 2, 1–64.CrossRefGoogle Scholar
Banks, W. H. H. & Zaturska, M. B. 1992 On flow through a porous annular pipe. Phys. Fluids A 4 (6), 1131–1141.Google Scholar
Berger, S. A., Talbot, L. & Yao, L. S. 1983 Note on the motion of fluid in a curved pipe. Annu. Rev. Fluid Mech. 15, 461–512.Google Scholar
Boshier, F. A. T. & Mestel, A. J. 2014 Extended series solutions and bifurcations of the Dean equations. J. Fluid Mech. 739, 179–195.Google Scholar
Boshier, F. A. T. & Mestel, A. J. 2017 Complex solutions of the Dean equations and non-uniqueness at all Reynolds numbers. J. Fluid Mech. 818, 241–259.Google Scholar
Boussinesq, J. 1897 Théorie de L’Écoulement Tourbillonnant Et Tumultueux Des Liquides Dans Les Lits Rectilignes a Grande Section. Gauthier-Villars.Google Scholar
Chan, T. F. 1984 Newton-like pseudo-arclength methods for computing simple turning points. SIAM J. Sci. Stat. Comput. 5 (1), 135–148.Google Scholar
Childress, S., Ierley, G. R., Spiegel, E. A. & Young, W. R. 1989 Blow-up of unsteady two-dimensional Euler and Navier–Stokes solutions having stagnation-point form. J. Fluid Mech. 203, 1–22.CrossRefGoogle Scholar
Dean, W. R. 1927 Note on the motion of fluid in a curved pipe. Lond. Edinb. Dublin Philos. Mag. J. Sci. 4 (20), 208–223.Google Scholar
Domb, C. & Sykes, M. F. 1957 On the susceptibility of a ferromagnetic above the Curie point. Proc. R. Soc. Lond. A 240 (1221), 214–228.Google Scholar
Drazin, P. G. & Tourigny, Y. 1996 Numerical study of bifurcations by analytic continuation of a function defined by a power series. SIAM J. Appl. Maths 56 (1), 1–18.Google Scholar
Prusa, J. & Yao, L. S. 1982 Numerical solution for fully developed flow in heated curved tubes. J. Fluid Mech. 123, 503–522.Google Scholar
Sharma, S., Coetzee, E. B., Lowenberg, M. H., Neild, S. A. & Krauskopf, B. 2015 Numerical continuation and bifurcation analysis in aircraft design: an industrial perspective. Phil. Trans. R. Soc. Lond. A 373 (2051), 20140406.Google ScholarPubMed
Smirnov, E. M. 1981 Self-similar solutions of Navier–Stokes equations for rotational flow of incompressible fluid in a round pipe. Z. Angew. Math. Mech. J. Appl. Math. Mech. 45 (5), 623–627.Google Scholar
Squire, H. B. 1951 The round laminar jet. Q. J. Mech. Appl. Maths 4 (3), 321–329.CrossRefGoogle Scholar
Subramanian, P., Brausch, O., Daniels, K. E., Bodenschatz, E., Schneider, T. M. & Pesch, W. 2016 Spatio-temporal patterns in inclined layer convection. J. Fluid Mech. 794, 719–745.Google Scholar
Terekhov, V. I. & Ekaid, A. L. 2011 Laminar natural convection between vertical isothermal heated plates with different temperatures. J. Engng Thermophys. 20 (4), 416–433.Google Scholar
Van Dyke, M. 1974 Analysis and improvement of perturbation series. Q. J. Mech. Appl. Maths 27 (4), 423–450.Google Scholar
Vaz, R. H., Boshier, F. A. T. & Mestel, A. J.2018 Dynamos in an annulus with fields linear in the axial coordinate. Geophys. Astrophys. Fluid Dyn. doi:10.1080/03091929.2018.1466882.CrossRefGoogle Scholar
Vyskrebtsov, V. G. 2001 New exact solutions of the Navier–Stokes equations for axisymmetric automodel flows of fluids. J. Math. Sci. 104 (5), 1456–1463.CrossRefGoogle Scholar
Weidman, P. 2016 Axisymmetric rotational stagnation point flow impinging on a radially stretching sheet. Intl J. Non-Linear Mech. 82, 1–5.Google Scholar
Yao, L. S. & Berger, S. A. 1978 Flow in heated curved pipes. J. Fluid Mech. 88, 339–354.CrossRefGoogle Scholar
Yuan, S. W. & Finkelstein, A. B. 1956 Laminar pipe flow with injection and suction through a porous wall. Trans. ASME 78, 719–724.Google Scholar
Zaturska, M. B., Drazin, P. G. & Banks, W. H. H. 1988 On the flow of a viscous fluid driven along a channel by suction at porous walls. Fluid Dyn. Res. 4 (3), 151–178.Google Scholar