Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T12:54:49.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Wave adjustment: general concept and examples

Published online by Cambridge University Press:  18 August 2015

G. M. Reznik
G. M. Reznik*
Affiliation:
P. P. Shirshov Institute of Oceanology, Russian Academy of Sciences, 36 Nakhimovskiy Prospekt, Moscow 117997, Russia
*
†Email address for correspondence: greznikmd@yahoo.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We formulate a general theory of wave adjustment applicable to any physical system (not necessarily a hydrodynamic one), which, being linearized, possesses linear invariants and a complete system of waves harmonically depending on the time $t$. The invariants are determined by the initial conditions and are zero for the waves, which, therefore, do not transport and affect the invariants. The evolution of such a system can be represented naturally as the sum of a stationary component with non-zero invariants and a non-steady wave part with zero invariants. If the linear system is disturbed by a small perturbation (linear or nonlinear), then the state vector of the system is split into slow balanced and fast wave components. Various scenarios of the wave adjustment are demonstrated with fairly simple hydrodynamic models. The simplest scenario, called ‘fast radiation’, takes place when the waves rapidly (their group speed 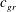$c_{gr}$ greatly exceeds the slow flow velocity 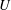$U$) radiate away from the initial perturbation and do not interact effectively with the slow component. As a result, at large times, after the waves propagate away, the residual flow is slow and described by a balanced model. The scenario is exemplified by the three-dimensional non-rotating barotropic flow with a free surface. A more complicated scenario, called ‘nonlinear trapping’, occurs if oscillations with small group speed 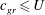$c_{gr}\leqslant U$ are present in the wave spectrum. In this case, after nonlinear wave adjustment, the state vector is a superposition of the slow balanced component and oscillations with small 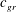$c_{gr}$ trapped by this component. An example of this situation is the geostrophic adjustment of a three-dimensional rotating barotropic layer with a free surface. In the third scenario, called ‘incomplete splitting’, the wave adjustment is accompanied by non-stationary boundary layers arising near rigid and internal boundaries at large times. The thickness of such a layer tends to zero and cross-gradients of physical parameters in the layer tend to infinity as 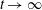$t\rightarrow \infty$. The layer is an infinite number of wave modes whose group speed tends to zero as the mode number tends to infinity. In such a system, complete splitting of motion into fast and slow components is impossible even in the linear approximation. The scenario is illustrated by an example of stratified non-rotating flow between two rigid lids. The above scenarios describe, at least, the majority of known cases of wave adjustment.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 779 , 25 September 2015 , pp. 514 - 543
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, J. S. 1993 Iterated geostrophic intermediate models. J. Phys. Oceanogr. 23, 2447–2461.Google Scholar
Babin, A., Mahalov, A. & Nikolaenko, B. 1998 Global splitting and regularity of rotating shallow-water equations. Eur. J. Mech. (B/Fluids) 15 (3), 291–300.Google Scholar
Balmforth, N. J., Llewellyn Smith, S. G. & Young, W. R. 1998 Enhanced dispersion of near-inertial waves in an idealized geostrophic flow. J. Mar. Res. 56, 1–40.Google Scholar
Balmforth, N. J. & Young, W. R. 1999 Radiative damping of near-inertial oscillations in the mixed layer. J. Mar. Res. 57, 561–584.Google Scholar
Daley, R. 1981 Normal mode initialization. Rev. Geophys. Space Phys. 19, 450–468.Google Scholar
Embid, P. F. & Majda, A. J. 1996 Averaging over fast gravity waves for geophysical flows with arbitrary potential vorticity. Commun. Part. Diff. Equ. 21, 619–658.Google Scholar
Gent, P. R. & McWilliams, J. C. 1983 Regimes of validity for balanced models. Dyn. Atmos. Oceans 7, 167–183.Google Scholar
Hoskins, B. J. 1975 The geostrophic momentum approximation and the semigeostrophic equations. J. Atmos. Sci. 32, 233–242.2.0.CO;2>CrossRefGoogle Scholar
Il’in, A. M. 1970 Asymptotic properties of a solution of a boundary-value problem. Math. Notes 8, 625–632.Google Scholar
Il’in, A. M. 1972 On the behaviour of the solution of a boundary-value problem when $t\rightarrow \infty$ . Math. USSR, Sb. 16, 545–572.Google Scholar
Kalashnick, M. V. 2004 Geostrophic adjustment and frontogenesis in the continuously stratified fluid. Dyn. Atmos. Oceans 38 (1), 1–37.Google Scholar
Kamenkovich, V. M. & Kamenkovich, I. V. 1993 On the evolution of Rossby waves, generated by wind stress in a closed basin, incorporating total mass conservation. Dyn. Atmos. Oceans 18, 67–103.Google Scholar
Kamke, E. 1976 Handbook of Ordinary Differential Equations. Chelsea.Google Scholar
Klein, P. & Llewellyn-Smith, S. 2001 Horizontal dispersion of near-inertial oscillations in a turbulent mesoscale eddy field. J. Mar. Res. 59, 697–723.Google Scholar
Klein, P., Llewellyn-Smith, S. & Lapeyre, G. 2004 Organization of near-inertial energy by an eddy field. Q. J. R. Meteorol. Soc. 130, 1153–1166.CrossRefGoogle Scholar
Leith, C. E. 1980 Nonlinear normal mode initialization and quasi-geostrophic theory. J. Atmos. Sci. 37, 958–968.Google Scholar
Lighthill, J. 1996 Internal waves and related initial-value problems. Dyn. Atmos. Oceans 23, 3–17.Google Scholar
Lynch, P. 1989 The slow motion. Q. J. R. Meteorol. Soc. 115, 201–219.Google Scholar
McWilliams, J. C. 1988 Vortex generation through balanced adjustment. J. Phys. Oceanogr. 18, 1178–1192.Google Scholar
McWilliams, J. C. 2006 Fundamentals of Geophysical Fluid Dynamics. Cambridge University Press.Google Scholar
Miropol’sky, Y. Z. 2001 Dynamics of Internal Gravity Waves in the Ocean. Kluwer.Google Scholar
Mohebalhojeh, A. R. & Dritschell, D. G. 2001 Hierarchies of balanced conditions for the $f$ -plane shallow-water equations. J. Atmos. Sci. 58, 2411–2426.Google Scholar
Monin, A. S. & Obukhov, A. M. 1958 Slight fluctuations of the atmosphere and adaptation of meteorological fields. Izv. Akad. Nauk SSSR Phys. Solid Earth 11, 786–791.Google Scholar
Morse, M. & Feshbach, H. 1953 Methods of Theoretical Physics. p. 1. McGraw-Hill.Google Scholar
Obukhov, A. M. 1949 On the question of the geostrophic wind. Izv. Akad. Nauk SSSR Geogr. Geofiz. 13 (4), 281–306; (in Russian).Google Scholar
Pedlosky, J. 1984 The equations for geostrophic motion in the ocean. J. Phys. Oceanogr. 14, 448–455.Google Scholar
Reznik, G. M. 2013 Linear dynamics of a stably-neutrally stratified ocean. J. Mar. Res. 71 (4), 253–288.Google Scholar
Reznik, G. M. 2014a Geostrophic adjustment with gyroscopic waves: barotropic fluid without traditional approximation. J. Fluid Mech. 743, 585–605.Google Scholar
Reznik, G. M. 2014b Geostrophic adjustment with gyroscopic waves: stably neutrally stratified fluid without the traditional approximation. J. Fluid Mech. 747, 605–634.Google Scholar
Reznik, G. M. & Grimshaw, R. 2002 Nonlinear geostrophic adjustment in the presence of a boundary. J. Fluid Mech. 471, 257–283.Google Scholar
Reznik, G. M. & Sutyrin, G. G. 2005 Non-conservation of geosrophic mass in the presence of a long boundary and the related Kelvin wave. J. Fluid Mech. 527, 235–264.Google Scholar
Reznik, G. M. & Zeitlin, V.2007 Asymptotic methods with applications to the fast–slow splitting and the geostrophic adjustment. In Nonlinear Dynamics of Rotating Shallow Water: Methods and Advances. (ed. V. Zeitlin). Edited Series on Advances in Nonlinear Science and Complexity (series ed. A. C. J. Luo & G. Zaslavsky), vol. 2, pp. 47–120. Elsevier.Google Scholar
Reznik, G. M., Zeitlin, V. & Ben Jelloul, M. 2001 Nonlinear theory of geostrophic adjustment. Part 1. Rotating shallow-water model. J. Fluid Mech. 445, 93–120.Google Scholar
Rossby, C. G. 1938 On the mutual adjustment of pressure and velocity distributions in certain simple current systems. J. Mar. Res. 1, 239–263.Google Scholar
Salmon, R. 1998 Lectures on Geophysical Fluid Dynamics. Oxford University Press.Google Scholar
Temperton, C. 1988 Implicit normal mode initialization. Mon. Weath. Rev. 116, 1013–1031.Google Scholar
Warn, T., Bokhove, O., Shepherd, T. G. & Vallis, G. K. 1995 Rossby number expansions, slaving principles, and balanced dynamics. Q. J. R. Meteorol. Soc. 121, 723–739.Google Scholar
Wingate, B. A., Embid, P., Holmes-Cerfon, M. & Taylor, M. A. 2011 Low Rossby limiting dynamics for stably stratified flow with finite Froude number. J. Fluid Mech. 676, 546–571.Google Scholar
Young, W. R. & Ben Jelloul, M. 1997 Propagation of near-inertial oscillations through a geostrophic flow. J. Mar. Res. 55, 735–766.Google Scholar
Zeitlin, V., Reznik, G. M. & Ben Jelloul, M. 2003 Nonlinear theory of geostrophic adjustment. Part 2. Two-layer and continuously stratified primitive equations. J. Fluid Mech. 491, 207–228.Google Scholar