Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-18T04:17:23.620Z Has data issue: false hasContentIssue false
  • English
  • Français

Waves from an oscillating point source with a free surface in the presence of a shear current

Published online by Cambridge University Press:  31 May 2016

Simen Å. Ellingsen Open the ORCID record for Simen Å. Ellingsen [Opens in a new window]  and
Peder A. Tyvand
Simen Å. Ellingsen*
Affiliation:
Department of Energy and Process Engineering, Norwegian University of Science and Technology, N-7491 Trondheim, Norway
Peder A. Tyvand
Affiliation:
Department of Mathematical Sciences and Technology, Norwegian University of Life Sciences, N-1432 Ås, Norway
*
†Email address for correspondence: simen.a.ellingsen@ntnu.no
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate analytically the linearised water wave radiation problem for an oscillating submerged point source in an inviscid shear flow with a free surface. A constant depth is taken into account and the shear flow increases linearly with depth. The surface velocity relative to the source is taken to be zero, so that Doppler effects are absent. We solve the linearised Euler equations to calculate the resulting wave field as well as its far-field asymptotics. For values of the Froude number 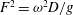$F^{2}={\it\omega}^{2}D/g$ (where 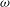${\it\omega}$ is the oscillation frequency, 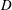$D$ is the submergence depth and 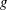$g$ is the gravitational acceleration) below a resonant value $F_{res}^{2}$, the wave field splits cleanly into separate contributions from regular dispersive propagating waves and non-dispersive ‘critical waves’ resulting from a critical layer-like street of flow structures directly downstream of the source. In the subresonant regime, the regular waves behave like sheared ring waves, while the critical layer wave forms a street with a constant width of order 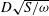$D\sqrt{S/{\it\omega}}$ (where 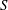$S$ is the shear flow vorticity) and is convected downstream at the fluid velocity at the depth of the source. When the Froude number approaches its resonant value, the downstream critical and regular waves resonate, producing a train of waves of linearly increasing amplitude contained within a downstream wedge.

JFM classification

Waves/Free-surface Flows: Critical layers Waves/Free-surface Flows: Shear waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 232 - 255
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bender, C. M. & Orszag, S. A. 1991 Advanced Mathematical Methods for Scientists and Engineers. Springer.Google Scholar
Booker, J. R. & Bretherton, F. P. 1967 The critical layer for internal gravity waves in a shear flow. J. Fluid Mech. 27, 513–539.CrossRefGoogle Scholar
Constantin, A. 2011 Two-dimensionality of gravity water flows of constant nonzero vorticity beneath a surface wave train. Eur. J. Mech. (B/Fluids) 30, 12–16.CrossRefGoogle Scholar
Constantin, A. & Varvaruca, E. 2011 Steady periodic water waves with constant vorticity: regularity and local bifurcation. Arch. Rat. Mech. Anal. 199, 33–67.CrossRefGoogle Scholar
Dyer, K. R. 1971 Current velocity profiles in a tidal channel. Geophys. J. Intl 22, 153–161.CrossRefGoogle Scholar
Ehrnström, M. & Villari, G. 2008 Linear water waves with vorticity: rotational features and particle paths. J. Differ. Equ. 244, 1888–1909.Google Scholar
Ellingsen, S. Å. 2014a Initial surface disturbance on a shear current: the Cauchy–Poisson problem with a twist. Phys. Fluids 26, 082104.Google Scholar
Ellingsen, S. Å. 2014b Ship waves in the presence of uniform vorticity. J. Fluid Mech. 742, R2.Google Scholar
Ellingsen, S. Å. 2016 Oblique waves on a vertically sheared current are rotational. Eur. J. Mech. (B/Fluids) 56, 156–160.CrossRefGoogle Scholar
Ellingsen, S. Å. & Brevik, I. 2014 How linear surface waves are affected by a current with constant vorticity. Eur. J. Phys. 35, 025005.Google Scholar
Ellingsen, S. Å. & Tyvand, P. A. 2016 Oscillating line source in a shear flow with a free surface: critical layer-like contributions. J. Fluid Mech. 798, 201–231; (Preceding paper, referred to in the text as E&T).Google Scholar
Faltinsen, O. M. 1990 Sea Loads on Ships and Offshore Structures. Cambridge University Press.Google Scholar
Johnson, R. S. 1990 Ring waves on the surface of shear flows: a linear and nonlinear theory. J. Fluid Mech. 215, 145–160.Google Scholar
Jones, I. S. F. & Toba, Y.(Eds) 2001 Wind Stress Over the Ocean. Cambridge University Press.CrossRefGoogle Scholar
Kochin, N. E. 1939 The two-dimensional problem of steady oscillations of bodies under the free surface of a heavy incompressible fluid. Izv. Akad. Nauk SSSR, Otdel. Tekhn. Nauk 4, 37–62.Google Scholar
Kochin, N. E. 1940 The theory of waves generated by oscillations of a body under the free surface of a heavy incompressible fluid. Uchenye Zapiski Moskov Gos. Univ. 46, 86–106.Google Scholar
Li, Y. & Ellingsen, S. Å. 2015 Initial value problems for water waves in the presence of a shear current. In Proceedings of the 25th International Offshore and Polar Engineering Conference (ISOPE), vol. 3, pp. 543–549. The International Society of Offshore and Polar Engineers (ISOPE).Google Scholar
Li, Y. & Ellingsen, S. Å. 2016 Ship waves on uniform shear current at finite depth: wave resistance and critical velocity. J. Fluid Mech. 791, 539–567.CrossRefGoogle Scholar
Lighthill, J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
Mellor, G. 2003 The three-dimensional current and surface wave equations. J. Phys. Oceanogr. 33, 1978–1989.Google Scholar
Newman, J. N. 1977 Marine Hydrodynamics. MIT Press.Google Scholar
Peregrine, D. H. 1976 Interaction of water waves and currents. Adv. Appl. Mech. 16, 9–117.Google Scholar
Shemdin, O. H. 1972 Wind-generated current and phase speed of wind waves. J. Phys. Oceanogr. 2, 411–419.2.0.CO;2>CrossRefGoogle Scholar
Shrira, V. I. 1993 Surface waves on shear currents: solution of the boundary-value problem. J. Fluid Mech. 252, 565–584.Google Scholar
Soulsby, R. L., Hamm, L., Klopman, G., Myrhaug, D., Simons, R. R. & Thomas, G. P. 1993 Wave–current interaction within and outside the bottom boundary layer. Coast. Engng 21, 41–69.Google Scholar
Thomson, Sir W. 1880 On a disturbing infinity in Lord Rayleigh’s solution for waves in a plan vortex stratum. Nature 23, 45–46.Google Scholar
Tyvand, P, A. & Lepperød, M. E. 2014 Oscillatory line source for water waves in shear flow. Wave Motion 51, 505–516.Google Scholar
Tyvand, P. A. & Lepperød, M. E. 2015 Doppler effects of an oscillating line source in shear flow with a free surface. Wave Motion 52, 103–119.CrossRefGoogle Scholar
Wahlén, E. 2009 Steady water waves with a critical layer. J. Differ. Equ. 246, 2468–2483.Google Scholar
Wehausen, J. W. & Laitone, E. V. 1960 Surface waves. In Fluid Dynamics III (ed. Flügge, S.), Encyclopedia of Physics, vol. IX, pp. 446–778. Springer.Google Scholar

Ellingsen and Tyvand supplementary movie

Movie animation of wave pattern from top panel of Figure 5 or article. With a low value of sigma, the wave pattern is completely dominated by the regular ring wave which is only slightly asymmetrical.

Download Ellingsen and Tyvand supplementary movie(Video)
Video 1.2 MB

Ellingsen and Tyvand supplementary movie

Movie animation of wave pattern from Figure 5b of article. With sigma=0.5, a critical layer "wave" is clearly visible, and the regular waves are visibly sheared. Flow is from right to left while the surface is at rest.

Download Ellingsen and Tyvand supplementary movie(Video)
Video 1.3 MB

Ellingsen and Tyvand supplementary movie

Movie animation of wave pattern from Figure 5c of article. An even higher value of sigma gives a more prominent critical layer and a more strongly sheared pattern of regular ring waves. Flow is from right to left while the surface is at rest.

Download Ellingsen and Tyvand supplementary movie(Video)
Video 1.1 MB

Ellingsen and Tyvand supplementary movie

The far-field "critical waves" shown in Figure 7 of article, for increasing values of sigma. See main article for more information and discussion.

Download Ellingsen and Tyvand supplementary movie(Video)
Video 739.6 KB

Ellingsen and Tyvand supplementary movie

Movie animation of Figure 9 of the article, showing the transition from sub-resonant to super resonant wave patterns. See article for more information and discussion.

Download Ellingsen and Tyvand supplementary movie(Video)
Video 958.7 KB

Ellingsen and Tyvand supplementary movie

Movie animation of four of the panels of Figure 10 of the article showing the flow near resonance for increasing values of sigma. See Figure 10 for further information and article text for discussion.

Download Ellingsen and Tyvand supplementary movie(Video)
Video 876.7 KB