Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-06-26T18:02:06.385Z Has data issue: false hasContentIssue false
  • English
  • Français

Assessment of inner–outer interactions in the urban boundary layer using a predictive model

Published online by Cambridge University Press:  18 July 2019

Karin Blackman Open the ORCID record for Karin Blackman [Opens in a new window] ,
Laurent Perret  and
Romain Mathis Open the ORCID record for Romain Mathis [Opens in a new window]
Karin Blackman*
Affiliation:
Ecole Centrale de Nantes, LHEEA, 1, rue de la Noe, BP 92101, Nantes, 44321, France
Laurent Perret
Affiliation:
Ecole Centrale de Nantes, LHEEA, 1, rue de la Noe, BP 92101, Nantes, 44321, France
Romain Mathis
Affiliation:
Ecole Centrale de Nantes, LHEEA, 1, rue de la Noe, BP 92101, Nantes, 44321, France
*
†Email address for correspondence: kblackma@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Urban-type rough-wall boundary layers developing over staggered cube arrays with plan area packing density, 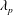$\unicode[STIX]{x1D706}_{p}$, of 6.25 %, 25 % or 44.4 % have been studied at two Reynolds numbers within a wind tunnel using hot-wire anemometry (HWA). A fixed HWA probe is used to capture the outer-layer flow while a second moving probe is used to capture the inner-layer flow at 13 wall-normal positions between 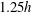$1.25h$ and 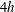$4h$ where 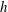$h$ is the height of the roughness elements. The synchronized two-point HWA measurements are used to extract the near-canopy large-scale signal using spectral linear stochastic estimation and a predictive model is calibrated in each of the six measurement configurations. Analysis of the predictive model coefficients demonstrates that the canopy geometry has a significant influence on both the superposition and amplitude modulation. The universal signal, the signal that exists in the absence of any large-scale influence, is also modified as a result of local canopy geometry suggesting that although the nonlinear interactions within urban-type rough-wall boundary layers can be modelled using the predictive model as proposed by Mathis et al. (J. Fluid Mech., vol. 681, 2011, pp. 537–566), the model must be however calibrated for each type of canopy flow regime. The Reynolds number does not significantly affect any of the model coefficients, at least over the limited range of Reynolds numbers studied here. Finally, the predictive model is validated using a prediction of the near-canopy signal at a higher Reynolds number and a prediction using reference signals measured in different canopy geometries to run the model. Statistics up to the fourth order and spectra are accurately reproduced demonstrating the capability of the predictive model in an urban-type rough-wall boundary layer.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 875 , 25 September 2019 , pp. 44 - 70
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R., Meinhart, C. & Tomkins, C. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Anderson, W. 2016 Amplitude modulation of streamwise velocity fluctuations in the roughness sublayer: evidence from large-eddy simulations. J. Fluid Mech. 789, 567–588.Google Scholar
Awasthi, A. & Anderson, W. 2018 Numerical study of turbulent channel flow perturbed by spanwise topographic heterogeneity: amplitude and frequency modulation within low- and high-momentum pathways. Phys. Rev. Fluids 3, 044602.Google Scholar
Baars, W., Hutchins, N. & Marusic, I. 2016a Spectral stochastic estimation of high-Reynolds-number wall-bounded turbulence for a refined inner-outer interaction model. Phys. Rev. Fluids 1, 1–23.Google Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2016b Spectral stochastic estimation of high-Reynolds-number wall-bounded turbulence for a refined inner-outer interaction model. Phys. Rev. Fluids 1, 054406.Google Scholar
Baars, W. J., Talluru, K. M., Hutchins, N. & Marusic, I. 2015 Wavelet analysis of wall turbulence to study large-scale modulation of small scale. Exp. Fluids 56 (188), 1–15.Google Scholar
Basley, J., Perret, L. & Mathis, R. 2018 Spatial modulations of kinetic energy in the roughness sublayer. J. Fluid Mech. 850, 584–610.Google Scholar
Basley, J., Perret, L. & Mathis, R. 2019 Structure of high Reynolds number boundary layers over cube canopies. J. Fluid Mech. 870, 460–491.Google Scholar
Blackman, K. & Perret, L. 2016 Non-linear interactions in a boundary layer developing over an array of cubes using stochastic estimation. Phys. Fluids 28, 095108.Google Scholar
Blackman, K., Perret, L. & Calmet, I. 2018 Energy transfer and non-linear interactions in an urban boundary layer using stochastic estimation. J. Turbul. 19, 849–867.Google Scholar
Blackman, K., Perret, L. & Savory, E. 2015 Effect of upstream flow regime on street canyon flow mean turbulence statistics. Environ. Fluid Mech. 15, 823–849.Google Scholar
Blackman, K., Perret, L. & Savory, E. 2017 Effects of upstream-flow regime and canyon aspect ratio on non-linear interactions between a street-canyon flow and the overlying boundary layer. Boundary Layer Meteorol. 169, 537–558.Google Scholar
Cheng, H. & Castro, I. P. 2002 Near wall flow over urban-like roughness. Boundary Layer Meteorol. 104, 229–259.Google Scholar
Coceal, O., Dobre, A., Thomas, T. G. & Belcher, S. E. 2007 Structure of turbulent flow over regular arrays of cubical roughness. J. Fluid Mech. 589, 375–409.Google Scholar
Duvvuri, S. & McKeon, B. 2015 Triadic scale interactions in a turbulent boundary layer. J. Fluid Mech. 767, R4.Google Scholar
Ghisalberti, M. 2009 Obstructed shear flows: similarities across systems and scales. J. Fluid Mech. 641, 51–61.Google Scholar
Grimmond, C. S. B. & Oke, T. R. 1999 Aerodynamic properties of urban areas derived from analysis of surface form. J. Appl. Meteorol. 38, 1262–1292.Google Scholar
Guala, M., Metzger, M. & McKeon, B. J. 2011 Interactions within the turbulent boundary layer at high Reynolds number. J. Fluid Mech. 666, 573–604.Google Scholar
Herpin, S., Perret, L., Mathis, R., Tanguy, C. & Lasserre, J.-J. 2018 Investigation of the flow inside an urban canopy immersed into an atmospheric boundary layer using laser Doppler anemometry. Exp. Fluids 59, 1–80.Google Scholar
Hultmark, M. & Smits, A. 2010 Temperature corrections for constant temperature and constant current hot-wire anemometers. Meas. Sci. Technol. 21, 105404.Google Scholar
Hussain, F. 1983 Coherent structures – reality and myth. Phys. Fluids 26, 2816–2838.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Inoue, M., Mathis, R., Marusic, I. & Pullin, D. 2012 Inner-layer intensities for the flat-plate turbulent boundary layer combining a predictive wall-model with large-eddy simulation. Phys. Fluids 24, 075102.Google Scholar
Macdonald, R. W., Griffiths, R. F. & Hall, D. J. 1998 An improved method for estimation of surface roughness of obstacle arrays. Atmos. Environ. 32, 857–1864.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2011 A wall-shear stress predictive model. In Proceedings of 13th European Turbulence Conference (ETC13) . J. Phys. Conf. Series 318, 012003.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011a A predictive inner-outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011b Relationship between turbulence modulation and skewness in wall bounded flows. In Proceedings of 7th Turbulent and Shear Flow Phenomena conference (TSFP7), Ottawa, Canada, vol. 1, pp. 1–6.Google Scholar
Mathis, R., Marusic, I., Hutchins, N. & Sreenivasan, K. R. 2011c The relationship between the velocity skewness and the amplitude modulation of the small scale by the large scale in turbulent boundary layers. Phys. Fluids 23 (12), 121702.Google Scholar
Nadeem, M., Lee, J. H., Lee, J. & Sung, H. J. 2015 Turbulent boundary layers over sparsely-spaced rod-roughened walls. Intl. J. Heat Fluid Flow 56, 16–27.Google Scholar
Pathikonda, G. & Christensen, K. T. 2017 Inner–outer interactions in a turbulent boundary layer overlying complex roughness. Phys. Rev. Fluids 2, 044603.Google Scholar
Perret, L., Basley, J., Mathis, R. & Piquet, T. 2019 Atmospheric boundary layers over urban-like terrains: influence of the plan density on the roughness sublayer dynamics. Boundary Layer Meteorol. 170, 205–234.Google Scholar
Perret, L. & Rivet, C. 2013 Dynamics of a turbulent boundary layer over cubical roughness elements: insight from PIV measurements and POD analysis. In Proceedings of 8th International Symposium on Turbulence and Shear Flow Phenomena (TSFP8), Poitiers, France, vol. 3, pp. 1–6.Google Scholar
Perret, L. & Rivet, C. 2018 A priori analysis of the performance of cross hot-wire probes in a rough wall boundary layer based on stereoscopic PIV. Exp. Fluids 59 (10), 153–176.Google Scholar
Rao, K. N., Narasimha, R. & Narayanan, M. A. B. 1971 The bursting phenomenon in a turbulent boundary layer. J. Fluid Mech. 48 (2), 339–352.Google Scholar
Reynolds, R. T. & Castro, I. P. 2008 Measurements in an urban-type boundary layer. Exp. Fluids 45, 141–156.Google Scholar
Salesky, S. T. & Anderson, W. 2018 Buoyancy effects on large-scale motions in convective atmospheric boundary layers: implications for modulation of near-wall processes. J. Fluid Mech. 856, 135–168.Google Scholar
Savory, E., Perret, L. & Rivet, C. 2013 Modelling considerations for examining the mean and unsteady flow in a simple urban-type street canyon. Meteorol. Atmos. Phys. 121, 1–16.Google Scholar
Squire, D. T., Morill-Winter, C., Hutchins, N., Schultz, M. P., Klewicki, J. C. & Marusic, I. 2016 Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers. J. Fluid Mech. 795, 210–240.Google Scholar
Takimoto, H., Inagaki, A., Kanda, M., Sato, A. & Michioka, T. 2013 Length-scale similarity of turbulent organized structures over surfaces with different roughness types. Boundary Layer Meteorol. 147 (2), 217–236.Google Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.Google Scholar
Townsend, A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar