Hostname: page-component-77c89778f8-sh8wx Total loading time: 0 Render date: 2024-07-21T10:24:33.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Convective diffusive mixing in concentration polarization: from Taylor dispersion to surface convection

Published online by Cambridge University Press:  08 July 2013

I. Rubinstein  and
B. Zaltzman
I. Rubinstein
Affiliation:
SIDEER, Blaustein Institutes for Desert Research, Ben-Gurion University of the Negev, Sede-Boqer Campus, 84990, Israel
B. Zaltzman*
Affiliation:
SIDEER, Blaustein Institutes for Desert Research, Ben-Gurion University of the Negev, Sede-Boqer Campus, 84990, Israel
*
†Email address for correspondence: boris@bgu.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse the steady-state convection–diffusion mixing of a solute by a creeping circulatory flow in a long sealed rectangular two-dimensional channel with impermeable sidewalls and fixed different solute concentrations at the two opposite edges. Solution circulation is due to a constant velocity slip along the sidewalls and a back flow along the channel axis. This simple model distils the essence of circulation in concentration polarization of an electrolyte solution under a DC electric current in a micro-channel sealed by an ion-selective element (a nano-channel or a cation exchange membrane). It is observed that in the slow circulation regime (small $Pe$ numbers) the solute flux through the channel is governed by the Taylor–Aris dispersion mechanism, i.e. the flux is driven by the cross-sectional average axial concentration gradient, whereas upon increase in 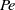$Pe$ this mechanism fails. The general question addressed is where the system goes after the breakdown of the Taylor–Aris dispersion regime. In order to find out the answer, the following specific questions have to be addressed. (1) How does the Taylor–Aris dispersion mechanism break down upon increase in 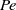$Pe$? (2) Why does it break down? (3) What is the role of the channel aspect ratio in this breakdown? The answers to these questions are obtained through analysing a hierarchy of suitable auxiliary model problems, including the unidirectional zero discharge channel flow and the circulatory analogue of plane-parallel Couette flow, for which most of the analysis is done. They may be summarized as follows. Upon increase in circulation velocity, the Taylor–Aris dispersion mechanism fails due to the formation of lateral non-uniformities of longitudinal solute concentration gradient driving the dispersion flux. These non-uniformities accumulate in protrusion-like disturbances of the solute concentration (wall fingers) emerging near the channel sidewall at the flow exit from the edge. Wall fingers propagate along the sidewalls with increase in 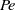$Pe$ and eventually reach the opposite channel edges, transforming into narrow surface convection layers. These layers, together with the edge diffusion layers, form a closed mass transport pattern carrying most of the mass flux through the channel with the bulk largely excluded from the transport. The formation of this pattern finalizes the transition from Taylor–Aris dispersion to the surface convection regime. For large circulation velocities, concentration distribution in the surface convection layers attains an oscillatory spiral structure reminiscent of thermal waves in heat conduction.

JFM classification

Convection: Convection in cavities Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Micro-/Nano-fluid dynamics: Microfluidics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 728 , 10 August 2013 , pp. 239 - 278
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acheson, D. J. 1990 Elementary Fluid Dynamics, 1st edn. Oxford University Press.CrossRefGoogle Scholar
Acrivos, A. & Goddard, J. D. 1965 Asymptotic expansions for laminar forced-convection heat and mass transfer. J. Fluid Mech. 23, 273–291.Google Scholar
Ångström, A. J. 1861 Neue Methode das Wärmeleitungsvermögen der Körper zu bestimmen. Ann. Phys. Chem. 114, 513–530.Google Scholar
Aris, R. 1956 On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. A 235, 67–77.Google Scholar
Balakotaiah, V. & Chang, H.-C. 1995 Dispersion of chemical solutes in chromatographs and reactors. Phil. Trans. Roy. Soc. Lond. A 351, 39–75.Google Scholar
Balakotaiah, V. & Chang, H.-C. 2003 Hyperbolic homogenized models for thermal and solutal dispersion. SIAM J. Appl. Maths 63, 1231–1258.Google Scholar
Batchelor, G. K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1, 177–190.Google Scholar
Bazant, M. Z., Dydek, E. V., Deng, D. S. & Mani, A. 2011 Method and apparatus for desalination and purification. US Patent Application 2011, 0308953.Google Scholar
Beals, R. 1981 Partial-range completeness and existence of solutions to two-way diffusion equations. J. Math. Phys. 22, 954–960.Google Scholar
Beals, R. 1985 Indefinite Sturm–Liouville problems and half-range completeness. J. Differ. Equ. 56, 391–407.CrossRefGoogle Scholar
Brenner, H. & Edwards, D. A. 1993 Macrotransport Processes, 1st edn. Butterworth–Heinemann.Google Scholar
Burggraf, O. 1966 Analytical and numerical studies of the structure of steady separated flows. J. Fluid Mech. 24, 113–151.CrossRefGoogle Scholar
Carslaw, H. S. 1921 Introduction to the Mathematical Theory of the Conduction of Heat in Solids, 2nd edn. Macmillan.Google Scholar
Chamarthy, P., Kumar, A., Cao, J. & Wereley, S. T. 2008 Fundamentals of diffusion in microfluidic systems. In Encyclopedia of Microfluidics and Nanofluidics (ed. Li, D.), pp. 761–768. Springer.CrossRefGoogle Scholar
Chang, H.-C. & Yeo, L. 2009 Electrokinetically Driven Microfluidics and Nanofluidics, 1st edn. Cambridge University Press.Google Scholar
Chen, C. H., Lin, H., Lele, S. K. & Santiago, J. G. 2005 Convective and absolute electrokinetic instability with conductivity gradients. J. Fluid Mech. 524, 263–303.Google Scholar
Dydek, E. V., Zaltzman, B., Rubinstein, I., Deng, D. S., Mani, A. & Bazant, M. Z. 2011 Overlimiting current in a microchannel. Phys. Rev. Lett. 107, 118301.Google Scholar
Goddard, J. D. & Acrivos, A. 1966 Asymptotic expansions for laminar forced-convection heat and mass transfer. Part 2. Boundary-layer flows. J. Fluid Mech. 24, 339–366.Google Scholar
Graetz, L. 1882 Über die Wärmeleitungsfähigkeit von Flüssigkeiten. Ann. Phys. 254, 79–94.CrossRefGoogle Scholar
Kim, S. J., Ko, S. H., Kang, K. H. & Han, J. 2010 Direct seawater desalination by ion concentration polarization. Nat. Nanotech. 5, 297–301.CrossRefGoogle ScholarPubMed
Kim, S. J., Ko, S. H., Kwak, R., Posner, J. D., Kang, K. H. & Han, J. 2012 Multi-vortical flow inducing electrokinetic instability in ion concentration polarization layer. Nanoscale 4, 7406–7410.CrossRefGoogle ScholarPubMed
Leal, L. G. 2007 Advanced Transport Phenomena, 1st edn. Cambridge University Press.CrossRefGoogle Scholar
Lin, H., Storey, B., Oddy, M., Chen, C. H. & Santiago, J. G. 2004 Instability of electrokinetic microchannel flows with conductivity gradients. Phys. Fluids 16, 1922–1935.CrossRefGoogle Scholar
Mani, A. & Bazant, M. Z. 2011 Deionization shocks in microstructures. Phys. Rev. E 84, 061504.CrossRefGoogle ScholarPubMed
Mani, A., Zangle, T. A. & Santiago, J. G. 2009 On the propagation of concentration polarization from microchannel–nanochannel interfaces. Part 1. Analytical model and characteristic analysis. Langmuir 25, 3898–3908.Google Scholar
Nunge, R. J. & Gill, W. N. 1966 An analytical study of laminar counterflow double-pipe heat exchangers. AIChE J. 12, 279–289.CrossRefGoogle Scholar
Pan, F. U. & Acrivos, A. 1968 Heat transfer at high Péclet numbers in regions of closed streamlines. Intl J. Heat Mass Transfer 11, 439–444.Google Scholar
Prandtl, L. 1905 Über Flüssigkeitsbewegung bei sehr kleiner Reibung. In Verhandlungen d. III. Internat. Math. Kongr. Heidelberg, 8–13 Aug. 1904, pp. 484–491. B. G. Teubner.Google Scholar
Rubinstein, I. & Shtilman, L. 1979 Voltage against current curves of cation exchange membranes. J. Chem. Soc. Faraday Trans. 75, 231–246.Google Scholar
Rubinstein, I. & Zaltzman, B. 2000 Electro-osmotically induced convection at a permselective membrane. Phys. Rev. E 62, 2238–2251.CrossRefGoogle Scholar
Rubinstein, I. & Zaltzman, B. 2010 Dynamics of extended space charge in concentration polarization. Phys. Rev. E 81, 061502.Google Scholar
Rubinstein, I., Zaltzman, B., Pretz, J. & Linder, C. 2002 Experimental verification of the electroosmotic mechanism of overlimiting conductance through a cation exchange electrodialysis membrane. Russ. Electrochem. 38, 853–864.CrossRefGoogle Scholar
Rubinstein, S. M., Manukyan, G., Staicu, A., Rubinstein, I., Zaltzman, B., Lammertink, R. G. H., Mugele, F. & Wessling, M. 2008 Direct observation of a nonequilibrium electro-osmotic instability. Phys. Rev. Lett. 101, 236101.Google Scholar
Samarskii, A. A. & Tikhonov, A. N. 1961 Partial Differential Equations of Mathematical Physics, 1st edn. Courier Dover.Google Scholar
Stone, H. A. & Brenner, H. 1999 Dispersion in flows with streamwise variations of mean velocity: radial flow. Ind. Engng Chem. Res. 38, 851–854.CrossRefGoogle Scholar
Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Yaroshchuk, A., Zholkovskiy, E., Pogodin, S. & Baulin, V. 2011 Coupled concentration polarization and electroosmotic circulation near micro/nanointerfaces: Taylor–Aris model of hydrodynamic dispersion and limits of its applicability. Langmuir 27, 11710–11721.Google Scholar
Yossifon, G. & Chang, H. C. 2008 Selection of non-equilibrium overlimiting currents: universal depletion layer formation dynamics and vortex instability. Phys. Rev. Lett. 101, 254501.Google Scholar
Zaltzman, B. & Rubinstein, I. 2007 Electro-osmotic slip and electroconvective instability. J. Fluid Mech. 579, 173–226.CrossRefGoogle Scholar
Zangle, T. A., Mani, A. & Santiago, J. G. 2009 On the propagation of concentration polarization from microchannel–nanochannel interfaces. Part 2. Numerical and experimental study. Langmuir 25, 3909–3916.Google Scholar