Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T16:32:30.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Cyclone–anticyclone asymmetry in gravity wave radiation from a co-rotating vortex pair in rotating shallow water

Published online by Cambridge University Press:  28 April 2015

Norihiko Sugimoto ,
K. Ishioka ,
H. Kobayashi  and
Y. Shimomura
Norihiko Sugimoto*
Affiliation:
Research and Education Center for Natural Sciences, Department of Physics, Keio University, 4-1-1 Hiyoshi, Kouhoku-ku, Yokohama, Kanagawa 223-8521, Japan
K. Ishioka
Affiliation:
Department of Geophysics, Graduate School of Science, Kyoto University, Kitashirakawa-Oiwake-cho, Sakyo-ku, Kyoto 606-8502, Japan
H. Kobayashi
Affiliation:
Research and Education Center for Natural Sciences, Department of Physics, Keio University, 4-1-1 Hiyoshi, Kouhoku-ku, Yokohama, Kanagawa 223-8521, Japan
Y. Shimomura
Affiliation:
Research and Education Center for Natural Sciences, Department of Physics, Keio University, 4-1-1 Hiyoshi, Kouhoku-ku, Yokohama, Kanagawa 223-8521, Japan
*
†Email address for correspondence: nori@phys-h.keio.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Cyclone–anticyclone asymmetry in spontaneous gravity wave radiation from a co-rotating vortex pair is investigated in an 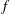$f$-plane shallow water system. The far field of gravity waves is derived analytically by analogy with the theory of aeroacoustic sound wave radiation (Lighthill theory). In the derived form, the Earth’s rotation affects not only the propagation of gravity waves but also their source. While the results correspond to the theory of vortex sound in the limit of 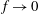$f\rightarrow 0$, there is an asymmetry in gravity wave radiation between cyclone pairs and anticyclone pairs for finite values of 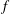$f$. Anticyclone pairs radiate gravity waves more intensely than cyclone pairs due to the effect of the Earth’s rotation. In addition, there is a local maximum of intensity of gravity waves from anticyclone pairs at an intermediate 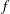$f$. To verify the analytical solution, a numerical simulation is also performed with a newly developed spectral method in an unbounded domain. The novelty of this method is the absence of wave reflection at the boundary due to a conformal mapping and a pseudo-hyperviscosity that acts like a sponge layer in the far field of waves. The numerical results are in excellent agreement with the analytical results even for finite values of 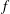$f$ for both cyclone pairs and anticyclone pairs.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Shallow water flows Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 772 , 10 June 2015 , pp. 80 - 106
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afanasyev, Y. D., Rhines, P. B. & Lindahl, E. G. 2008 Emission of inertial waves by baroclinically unstable flows: laboratory experiments with altimetric imaging velocimetry. J. Atmos. Sci. 65, 250–262.CrossRefGoogle Scholar
Bühler, O. & McIntyre, M. E. 2005 Wave capture and wave-vortex duality. J. Fluid Mech. 534, 67–95.CrossRefGoogle Scholar
Dritschel, D. G. & Vanneste, J. 2006 Instabilities of a shallow-water potential-vorticity front. J. Fluid Mech. 561, 237–254.CrossRefGoogle Scholar
Ford, R. 1994 Gravity wave radiation from vortex trains in rotating shallow water. J. Fluid Mech. 281, 81–118.CrossRefGoogle Scholar
Ford, R., McIntyre, M. E. & Norton, W. A. 2000 Balance and the slow quasimanifold: some explicit results. J. Atmos. Sci. 57, 1236–1254.2.0.CO;2>CrossRefGoogle Scholar
Fritts, D. C. & Alexander, M. J. 2003 Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 41, 1–59.CrossRefGoogle Scholar
Gryanik, V. M. 1983 Emission of sound by linear vortical filaments. Izv. Atmos. Ocean. Phys. 19, 150–152.Google Scholar
Harada, M. & Ishioka, K. 2011 Inertia–gravity wave radiation from an unstable Bickley jet in rotating two-layer shallow water. SOLA 7, 113–116.CrossRefGoogle Scholar
Holton, J. R., Haynes, P. H., McIntyre, M. E., Douglass, A. R., Road, R. B. & Pfister, L. 1995 Stratosphere–troposphere exchange. Rev. Geophys. 33, 403–439.CrossRefGoogle Scholar
Howe, M. S. 2003 Theory of Vortex Sound. Cambridge University Press.Google Scholar
Ishioka, K. 2008 A spectral method for unbounded domains and its application to wave equations in geophysical fluid dynamics. In IUTAM Symposium on Computational Physics and New Perspectives in Turbulence, pp. 291–296. Springer.CrossRefGoogle Scholar
Ishioka, K.2011 ispack-0.96. http://www.gfd-dennou.org/arch/ispack/, GFD Dennou Club 2011.Google Scholar
Jiménez, J. 1994 Hyperviscous vortices. J. Fluid Mech. 279, 169–176.CrossRefGoogle Scholar
Kitamura, Y. & Hirota, I. 1989 Small-scale disturbances in the lower stratosphere revealed by daily Rawin sonde observations. J. Met. Soc. Japan 67, 817–831.CrossRefGoogle Scholar
Knio, O. M., Collorec, L. & Juvé, D. 1995 Numerical study of sound emission by 2D regular and chaotic vortex configurations. J. Comput. Phys. 116, 226–246.CrossRefGoogle Scholar
Lahaye, N. & Zeitlin, V. 2012a Decaying vortex and wave turbulence in rotating shallow water mode, as follows from high-resolution direct numerical simulations. Phys. Fluids 24, 115106.CrossRefGoogle Scholar
Lahaye, N. & Zeitlin, V. 2012b Shock modon: a new type of coherent structure in rotating shallow water. Phys. Rev. Lett. 108, 044502.CrossRefGoogle ScholarPubMed
Lighthill, M. J. 1952 On the sound generated aerodynamically, I. Proc. R. Soc. Lond. A 211, 564–587.Google Scholar
Mariotti, A., Legras, B. & Dritschel, D. G. 1994 Vortex stripping and the erosion of coherent structures in two-dimensional flows. Phys. Fluids 6, 3954–3962.CrossRefGoogle Scholar
Matsushima, T. & Marcus, T. P. S. 1997 A spectral method for unbounded domains. J. Comput. Phys. 137, 321–345.CrossRefGoogle Scholar
May, P. T. 1996 The organization of convection in the rainbands of tropical cyclone Laurence. Mon. Weath. Rev. 124, 807–815.2.0.CO;2>CrossRefGoogle Scholar
McIntyre, M. E. 2009 Spontaneous imbalance and hybrid vortex-gravity structures. J. Atmos. Sci. 66, 1315–1325.CrossRefGoogle Scholar
Mitchell, B. E., Lele, S. K. & Moin, P. 1995 Direct computation of the sound from a compressible co-rotating vortex pair. J. Fluid Mech. 285, 181–202.CrossRefGoogle Scholar
Murakami, S.2008 Stability of the isolated vortex and gravity wave radiation in an $f$ -plane shallow water system. Master’s thesis, Kyoto University (in Japanese).Google Scholar
O’Sullivan, D. & Dunkerton, T. J. 1995 Generation of inertia–gravity waves in a simulated life cycle of baroclinic instability. J. Atmos. Sci. 52, 3695–3716.2.0.CO;2>CrossRefGoogle Scholar
Pfister, L. W., Chan, K. R., Bui, T. P., Bowen, S., Legg, M., Gary, B., Kelly, K., Proffitt, M. & Starr, W. 1993 Gravity waves generated by a tropical cyclone during the STEP Tropical Field Program: a case study. J. Geophys. Res. 98, 8611–8638.CrossRefGoogle Scholar
Plougonven, R. & Snyder, C. 2007 Inertia–gravity waves spontaneously generated by jets and fronts. Part I: different baroclinic life cycles. J. Atmos. Sci. 64, 2502–2520.CrossRefGoogle Scholar
Plougonven, R., Teitelbaum, H. & Zeitlin, V. 2003 Inertia gravity wave generation by the tropospheric midlatitude jet as given by the Fronts and Atlantic Storm-Track Experiment radio soundings. J. Geophys. Res. 108 (D21), 4686.Google Scholar
Plougonven, R. & Zeitlin, V. 2002 Internal gravity wave emission from a pancake vortex: an example of wave–vortex interaction in strongly stratified flows. Phys. Fluids 14, 1259–1268.CrossRefGoogle Scholar
Plougonven, R. & Zhang, F. 2014 Internal gravity waves from atmospheric jets and fronts. Rev. Geophys. 52, 33–76.CrossRefGoogle Scholar
Polvani, L. M., McWilliams, J. C., Spall, M. A. & Ford, R. 1994 The coherent strucutres of shallow water turbulence: deformation-radius effects, cyclone/anticyclone asymmetry and gravity wave generation. Chaos 4 (2), 177–186.CrossRefGoogle Scholar
Powell, A. 1964 Theory of vortex sound. J. Acoust. Soc. Am. 36, 177–195.CrossRefGoogle Scholar
Sato, K. 1994 A statistical study of the structure, saturation and sources of inertio-gravity waves in the lower stratosphere observed with the MU radar. J. Atmos. Terr. Phys. 56, 755–774.CrossRefGoogle Scholar
Sato, K. & Yoshiki, M. 2008 Gravity wave generation around the polar vortex in the stratosphere revealed by 3-hourly radiosonde observations at Syowa station. J. Atmos. Sci. 65, 3719–3735.CrossRefGoogle Scholar
Saujani, S. & Shepherd, T. G. 2002 Comments on ‘Balance and the slow quasimanifold: some explicit results’. J. Atmos. Sci. 59, 2874–2877.2.0.CO;2>CrossRefGoogle Scholar
Schecter, D. A. & Montgomery, M. T. 2004 Damping and pumping of a vortex Rossby wave in a monotonic cyclone: critical layer stirring versus inertia-buoyancy wave emission. Phys. Fluids 16, 1334–1348.CrossRefGoogle Scholar
Snyder, C., Muraki, D. J., Plougonven, R. & Zhang, F. 2007 Inertia–gravity waves generated within dipole vortex. J. Atmos. Sci. 64, 4417–4431.CrossRefGoogle Scholar
Stegner, A. & Dritschel, D. G. 2000 A numerical investigation of the stability of isolated shallow water vortices. J. Phys. Oceanogr. 30, 2562–2573.2.0.CO;2>CrossRefGoogle Scholar
Sugimoto, N. & Ishii, K. 2012 Spontaneous gravity wave radiation in a shallow water system on a rotating sphere. J. Met. Soc. Japan 90 (1), 101–125.CrossRefGoogle Scholar
Sugimoto, N., Ishioka, K. & Ishii, K. 2008 Parameter sweep experiments on spontaneous gravity wave radiation from unsteady rotational flow in an $f$ -plane shallow water system. J. Atmos. Sci. 65, 249–273.CrossRefGoogle Scholar
Sugimoto, N., Ishioka, K. & Yoden, S. 2007a Balance regimes for the stability of a jet in an $f$ -plane shallow water system. Fluid Dyn. Res. 39, 353–377.CrossRefGoogle Scholar
Sugimoto, N., Ishioka, K. & Yoden, S. 2007b Gravity wave radiation from unsteady rotational flow in an $f$ -plane shallow water system. Fluid Dyn. Res. 39, 731–754.CrossRefGoogle Scholar
Sugimoto, N., Takagi, M. & Matsuda, Y. 2014 Baroclinic instability in the Venus atmosphere simulated by GCM. J. Geophys. Res. Planets 119, 1950–1968.CrossRefGoogle Scholar
Uccelini, L. W. & Koch, S. E. 1987 The synoptic setting and possible energy sources for mesoscale wave disturbances. Mon. Weath. Rev. 115, 721–729.2.0.CO;2>CrossRefGoogle Scholar
Vanneste, J. 2008 Exponential smallness of inertia–gravity wave generation at small Rossby number. J. Atmos. Sci. 65, 1622–1637.CrossRefGoogle Scholar
Vanneste, J. 2013 Balance and spontanous wave generation in geophysical flows. Annu. Rev. Fluid Mech. 45, 147–172.CrossRefGoogle Scholar
Viúdez, Á. 2007 The origin of the stationary frontal wave packet spontaneously generated in rotating stratified vortex dipoles. J. Fluid Mech. 593, 359–383.CrossRefGoogle Scholar
Wang, S., Zhang, F. & Snyder, C. 2009 Generation and propagation of inertia–gravity waves from vortex dipoles and jets. J. Atmos. Sci. 66, 1294–1314.CrossRefGoogle Scholar
Williams, P. D., Haine, T. W. N. & Read, P. L. 2005 On the generation mechanisms of short-scale unbalanced modes in rotating two-layer flows with vertical shear. J. Fluid Mech. 528, 1–22.CrossRefGoogle Scholar
Williams, P. D., Haine, T. W. N. & Read, P. L. 2008 Inertia–gravity waves emitted from balanced flow: observations, properties, and consequences. J. Atmos. Sci. 65, 3453–3556.CrossRefGoogle Scholar
Williams, P. D., Read, P. L. & Haine, T. W. N. 2003 Spontaneous generation and impact of inertia–gravity waves in a stratified, two-layer shear flow. Geophys. Res. Lett. 30, 2255.CrossRefGoogle Scholar
Wu, D. L. & Eckermann, S. D. 2008 Global gravity wave variance from Aura MLS: characteristics and interpretation. J. Atmos. Sci. 65, 3695–3718.CrossRefGoogle Scholar
Yao, H. B., Zabusky, N. J. & Dritschel, D. G. 1995 High gradient phenomena in two-dimensional vortex interactions. Phys. Fluids 7, 539–548.CrossRefGoogle Scholar
Yasuda, Y., Sato, K. & Sugimoto, N. 2015a A theoretical study on the spontaneous radiation of inertia–gravity waves using the renormalization group method. Part I: derivation of the renormalization group equations. J. Atmos. Sci. 72, 957–983.CrossRefGoogle Scholar
Yasuda, Y., Sato, K. & Sugimoto, N. 2015b A theoretical study on the spontaneous radiation of inertia–gravity waves using the renormalization group method. Part II: verification of the theoretical equations by numerical simulation. J. Atmos. Sci. 72, 984–1009.CrossRefGoogle Scholar
Yoshiki, M. & Sato, K. 2000 A statistical study of gravity waves in the polar regions based on operational radiosonde data. J. Geophys. Res. 105, 17995–18011.CrossRefGoogle Scholar
Zeitlin, V. 1991 On the backreaction of acoustic radiation for distributed two-dimensional vortex structures. Phys. Fluids A3, 1677–1680.CrossRefGoogle Scholar
Zeitlin, V. 2007 Nonlinear Dynamics of Rotating Shallow Water: Methods and Advances. Elsevier.Google Scholar
Zhang, F. 2004 Generation of mesoscale gravity waves in upper tropospheric jet-front systems. J. Atmos. Sci. 61, 440–457.2.0.CO;2>CrossRefGoogle Scholar