Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T07:25:41.284Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent flow over transitionally rough surfaces with varying roughness densities

Published online by Cambridge University Press:  08 September 2016

M. MacDonald Open the ORCID record for M. MacDonald [Opens in a new window] ,
L. Chan ,
D. Chung Open the ORCID record for D. Chung [Opens in a new window] ,
N. Hutchins  and
A. Ooi
M. MacDonald*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
L. Chan
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
D. Chung
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
N. Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
A. Ooi
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: michael.macdonald@unimelb.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate rough-wall turbulent flows through direct numerical simulations of flow over three-dimensional transitionally rough sinusoidal surfaces. The roughness Reynolds number is fixed at 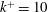$k^{+}=10$, where 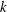$k$ is the sinusoidal semi-amplitude, and the sinusoidal wavelength is varied, resulting in the roughness solidity 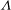$\unicode[STIX]{x1D6EC}$ (frontal area divided by plan area) ranging from 0.05 to 0.54. The high cost of resolving both the flow around the dense roughness elements and the bulk flow is circumvented by the use of the minimal-span channel technique, recently demonstrated by Chung et al. (J. Fluid Mech., vol. 773, 2015, pp. 418–431) to accurately determine the Hama roughness function, 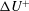$\unicode[STIX]{x0394}U^{+}$. Good agreement of the second-order statistics in the near-wall roughness-affected region between minimal- and full-span rough-wall channels is observed. In the sparse regime of roughness (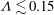$\unicode[STIX]{x1D6EC}\lesssim 0.15$) the roughness function increases with increasing solidity, while in the dense regime the roughness function decreases with increasing solidity. It was found that the dense regime begins when 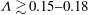$\unicode[STIX]{x1D6EC}\gtrsim 0.15{-}0.18$, in agreement with the literature. A model is proposed for the limit of 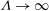$\unicode[STIX]{x1D6EC}\rightarrow \infty$, which is a smooth wall located at the crest of the roughness elements. This model assists with interpreting the asymptotic behaviour of the roughness, and the rough-wall data presented in this paper show that the near-wall flow is tending towards this modelled limit. The peak streamwise turbulence intensity, which is associated with the turbulent near-wall cycle, is seen to move further away from the wall with increasing solidity. In the sparse regime, increasing 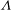$\unicode[STIX]{x1D6EC}$ reduces the streamwise turbulent energy associated with the near-wall cycle, while increasing 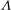$\unicode[STIX]{x1D6EC}$ in the dense regime increases turbulent energy. An analysis of the difference of the integrated mean momentum balance between smooth- and rough-wall flows reveals that the roughness function decreases in the dense regime due to a reduction in the Reynolds shear stress. This is predominantly due to the near-wall cycle being pushed away from the roughness elements, which leads to a reduction in turbulent energy in the region previously occupied by these events.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , pp. 130 - 161
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A. & Krogstad, P.-Å. 2001 Turbulence structure in boundary layers over different types of surface roughness. Fluid Dyn. Res. 28 (2), 139–157.CrossRefGoogle Scholar
Beavers, G. S. & Joseph, D. D. 1967 Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30 (01), 197–207.CrossRefGoogle Scholar
Breugem, W. P., Boersma, B. J. & Uittenbogaard, R. E. 2006 The influence of wall permeability on turbulent channel flow. J. Fluid Mech. 562 (1), 35–72.CrossRefGoogle Scholar
Chan, L., Macdonald, M., Chung, D., Hutchins, N. & Ooi, A. 2015 A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J. Fluid Mech. 771, 743–777.CrossRefGoogle Scholar
Chung, D., Chan, L., Macdonald, M., Hutchins, N. & Ooi, A. 2015 A fast direct numerical simulation method for characterising hydraulic roughness. J. Fluid Mech. 773, 418–431.Google Scholar
Coceal, O., Thomas, T. G., Castro, I. P. & Belcher, S. E. 2006 Mean flow and turbulence statistics over groups of urban-like cubical obstacles. Boundary-Layer Meteorol. 121 (3), 491–519.Google Scholar
De Marchis, M., Milici, B. & Napoli, E. 2015 Numerical observations of turbulence structure modification in channel flow over 2D and 3D rough walls. Intl J. Heat Fluid Flow 56, 108–123.Google Scholar
Efros, V. & Krogstad, P.-Å. 2011 Development of a turbulent boundary layer after a step from smooth to rough surface. Exp. Fluids 51 (6), 1563–1575.CrossRefGoogle Scholar
Flack, K. A. & Schultz, M. P. 2010 Review of hydraulic roughness scales in the fully rough regime. Trans. ASME J. Fluids Engng 132 (4), 041203.CrossRefGoogle Scholar
Flack, K. A. & Schultz, M. P. 2014 Roughness effects on wall-bounded turbulent flows. Phys. Fluids 26 (10), 101305.CrossRefGoogle Scholar
Flack, K. A., Schultz, M. P. & Rose, W. B. 2012 The onset of roughness effects in the transitionally rough regime. Intl J. Heat Fluid Flow 35, 160–167.CrossRefGoogle Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 071704.Google Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), L73–L76.CrossRefGoogle Scholar
García-Mayoral, R. & Jiménez, J. 2011 Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 678, 317–347.CrossRefGoogle Scholar
Grimmond, C. S. B. & Oke, T. R. 1999 Aerodynamic properties of urban areas derived from analysis of surface form. J. Appl. Meteorol. 38 (9), 1262–1292.Google Scholar
Hagishima, A., Tanimoto, J., Nagayama, K. & Meno, S. 2009 Aerodynamic parameters of regular arrays of rectangular blocks with various geometries. Boundary-Layer Meteorol. 132 (2), 315–337.Google Scholar
Ham, F. & Iaccarino, G.2004 Energy conservation in collocated discretization schemes on unstructured meshes. In Annual Research Briefs 2004, pp. 3–14. Center for Turbulence Research, Stanford University/NASA Ames.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.CrossRefGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Kanda, M., Moriwaki, R. & Kasamatsu, F. 2004 Large-eddy simulation of turbulent organized structures within and above explicitly resolved cube arrays. Boundary-Layer Meteorol. 112 (2), 343–368.CrossRefGoogle Scholar
Krumbein, W. C. & Monk, G. D. 1943 Permeability as a function of the size parameters of unconsolidated sand. Trans. Inst. Mining Met. Engrs 151 (01), 153–163.Google Scholar
Lee, J. H., Sung, H. J. & Krogstad, P.-Å. 2011 Direct numerical simulation of the turbulent boundary layer over a cube-roughened wall. J. Fluid Mech. 669, 397–431.Google Scholar
Leonardi, S. & Castro, I. P. 2010 Channel flow over large cube roughness: a direct numerical simulation study. J. Fluid Mech. 651, 519–539.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P. & Antonia, R. A. 2007 Properties of d-and k-type roughness in a turbulent channel flow. Phys. Fluids 19, 125101.CrossRefGoogle Scholar
Lien, F. S., Yee, E. & Wilson, J. D. 2005 Numerical modelling of the turbulent flow developing within and over a 3-D building array. Part II: a mathematical foundation for a distributed drag force approach. Boundary-Layer Meteorol. 114 (2), 245–285.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to Re 𝜏 = 4200. Phys. Fluids 26 (1), 011702.CrossRefGoogle Scholar
Macdonald, R. W. 2000 Modelling the mean velocity profile in the urban canopy layer. Boundary-Layer Meteorol. 97 (1), 25–45.Google Scholar
Macdonald, R. W., Griffiths, R. F. & Hall, D. J. 1998 An improved method for the estimation of surface roughness of obstacle arrays. Atmos. Environ. 32 (11), 1857–1864.CrossRefGoogle Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 197, 215–240.Google Scholar
Millward-Hopkins, J. T., Tomlin, A. S., Ma, L., Ingham, D. & Pourkashanian, M. 2011 Estimating aerodynamic parameters of urban-like surfaces with heterogeneous building heights. Boundary-Layer Meteorol. 141 (3), 443–465.Google Scholar
Moin, P. & Kim, J. 1982 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.Google Scholar
Napoli, E., Armenio, V. & De Marchis, M. 2008 The effect of the slope of irregularly distributed roughness elements on turbulent wall-bounded flows. J. Fluid Mech. 613, 385–394.Google Scholar
Nikuradse, J.1933 Laws of flow in rough pipes. Translation from German published 1950 as NACA Tech. Memo. 1292.Google Scholar
Oke, T. R 1988 Street design and urban canopy layer climate. Energy Build. 11 (1), 103–113.Google Scholar
Orlandi, P., Leonardi, S. & Antonia, R. A. 2006 Turbulent channel flow with either transverse or longitudinal roughness elements on one wall. J. Fluid Mech. 561, 279–305.Google Scholar
Placidi, M. & Ganapathisubramani, B. 2015 Effects of frontal and plan solidities on aerodynamic parameters and the roughness sublayer in turbulent boundary layers. J. Fluid Mech. 782, 541–566.Google Scholar
Raupach, M. R. 1994 Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Boundary-Layer Meteorol. 71 (1–2), 211–216.Google Scholar
Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44, 1–25.CrossRefGoogle Scholar
Rosti, M. E., Cortelezzi, L. & Quadrio, M. 2015 Direct numerical simulations of turbulent channel flow over porous walls. J. Fluid Mech. 784, 396–442.Google Scholar
Schlichting, H. 1936 Experimental investigation of the problem of surface roughness. Ing.-Arch. 7, 1–34; Translation from German published 1937 as NACA Tech. Memo. 823.Google Scholar
Schultz, M. P. & Flack, K. A. 2009 Turbulent boundary layers on a systematically varied rough wall. Phys. Fluids 21, 015104.Google Scholar
Spalart, P. R. & Mclean, J. D. 2011 Drag reduction: enticing turbulence, and then an industry. Phil. Trans. R. Soc. Lond. A 369 (1940), 1556–1569.Google ScholarPubMed
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Waigh, D. R. & Kind, R. J. 1998 Improved aerodynamic characterization of regular three-dimensional roughness. AIAA J. 36 (6), 1117–1119.CrossRefGoogle Scholar
Yang, X. I. A., Sadique, J., Mittal, R. & Meneveau, C. 2016 Exponential roughness layer and analytical model for turbulent boundary layer flow over rectangular-prism roughness elements. J. Fluid Mech. 789, 127–165.Google Scholar