Published online by Cambridge University Press: 08 January 2020
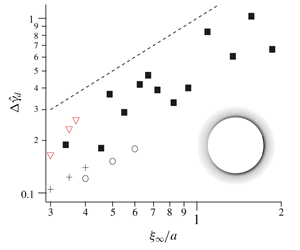
The drag coefficient of a rigid spherical particle deviates from Stokes law when it is put into a near-critical fluid mixture in the homogeneous phase with the critical composition. The deviation ( $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}_{d}$) is experimentally shown to depend approximately linearly on the correlation length of the composition fluctuation far from the particle (
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}_{d}$) is experimentally shown to depend approximately linearly on the correlation length of the composition fluctuation far from the particle ( $\unicode[STIX]{x1D709}_{\infty }$), and is suggested to be caused by the preferential adsorption between one component and the particle surface. In contrast, the dependence was shown to be much steeper in the previous theoretical studies based on the Gaussian free-energy density. In the vicinity of the particle, especially when the adsorption of the preferred component makes the composition strongly off-critical, the correlation length becomes very small as compared with
$\unicode[STIX]{x1D709}_{\infty }$), and is suggested to be caused by the preferential adsorption between one component and the particle surface. In contrast, the dependence was shown to be much steeper in the previous theoretical studies based on the Gaussian free-energy density. In the vicinity of the particle, especially when the adsorption of the preferred component makes the composition strongly off-critical, the correlation length becomes very small as compared with  $\unicode[STIX]{x1D709}_{\infty }$. This spatial inhomogeneity, not considered in the previous theoretical studies, can influence the dependence of
$\unicode[STIX]{x1D709}_{\infty }$. This spatial inhomogeneity, not considered in the previous theoretical studies, can influence the dependence of  $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}_{d}$ on
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}_{d}$ on  $\unicode[STIX]{x1D709}_{\infty }$. To examine this possibility, we here apply a renormalized local functional theory, describing the preferential adsorption in terms of the surface field. This theory was previously proposed to explain the interaction of walls immersed in a (near-)critical binary fluid mixture. The free-energy density in this theory, coarse-grained up to the local correlation length, has a very complicated dependence on the order parameter, as compared with the Gaussian free-energy density. Still, a concise expression of the drag coefficient, which was derived in one of the previous theoretical studies, turns out to be valid in the present formulation. We show that, as
$\unicode[STIX]{x1D709}_{\infty }$. To examine this possibility, we here apply a renormalized local functional theory, describing the preferential adsorption in terms of the surface field. This theory was previously proposed to explain the interaction of walls immersed in a (near-)critical binary fluid mixture. The free-energy density in this theory, coarse-grained up to the local correlation length, has a very complicated dependence on the order parameter, as compared with the Gaussian free-energy density. Still, a concise expression of the drag coefficient, which was derived in one of the previous theoretical studies, turns out to be valid in the present formulation. We show that, as  $\unicode[STIX]{x1D709}_{\infty }$ becomes larger, the dependence of
$\unicode[STIX]{x1D709}_{\infty }$ becomes larger, the dependence of  $\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}_{d}$ on
$\unicode[STIX]{x0394}\unicode[STIX]{x1D6FE}_{d}$ on  $\unicode[STIX]{x1D709}_{\infty }$ becomes distinctly gradual and close to the linear dependence.
$\unicode[STIX]{x1D709}_{\infty }$ becomes distinctly gradual and close to the linear dependence.