1. Introduction
Electro-desalting of crude oil is typically the first unit operation in crude refining, wherein electro-desalters, employing electric fields, are used to dewater brine droplets from crude oil emulsions (Chen et al. Reference Chen, Mohammed, Bailey, Luckham and Taylor1994; Eow & Ghadiri Reference Eow and Ghadiri2002; Less & Vilagines Reference Less and Vilagines2012; Anand et al. Reference Anand, Vashishtha, Shown, Patidar, Malhotra, Ghosh, Jaguste, Naik, Thaokar and Juvekar2018). The process leads to the removal of salt and water to an extent suitable for further processing of crude oil in a refinery. An electro-desalter typically has parallel electrodes generating a uniform electric field. The crude oil emulsion, when subjected to this field, results in electrocoalescence of the brine droplets that leads to their growth and subsequent separation from the emulsion by gravitational settling. It has been widely reported that, although strong electric fields hasten the approach of the water droplets, the droplets could, instead of coalescence, exhibit non-coalescence (Anand et al. Reference Anand, Roy, Naik, Juvekar and Thaokar2019; Roy, Anand & Thaokar Reference Roy, Anand and Thaokar2019). The phenomenon of coalescence of droplets under the effect of an electric field involves, (i) approach of the droplets, (ii) drainage of the liquid from between the droplets and (iii) formation of a bridge between the droplets. If the bridge thickens, it leads to coalescence of the two droplets (Atten Reference Atten1993). However, under certain conditions, especially under a strong electric field, the bridge could thin, instead of thickening, leading to breakage of the bridge, and this is referred to as non-coalescence. The process of coalescence, thus hindered, results in reduced efficiency of desalters/electrocoalescers and an optimum separation of oil and water is not achieved. Further, it prohibits use of strong electric fields in desalters/electrocoalescers.
Theoretical models were put forth by Bird et al. (Reference Bird, Ristenpart, Belmonte and Stone2009) and Bartlett, Généro & Bird (Reference Bartlett, Généro and Bird2015) wherein symmetric interactions between two equal sized droplets could lead to the formation of conical ends that could contact to form a liquid bridge. The Laplace pressure in this bridge depends upon the cone angle of the conical ends, and thereby on the shape (more accurately, on the two curvatures: azimuthal and meridional) of the bridge. A critical angle of ![]() $30.8^{\circ }$ was observed beyond which non-coalescence of droplets was observed.
$30.8^{\circ }$ was observed beyond which non-coalescence of droplets was observed.
While deciphering the physics behind the interaction of two equal sized droplets gives a fundamental idea about when droplets, suspended in oil under an electric field, exhibit coalescence or non-coalescence, in desalters, the emulsions are seldom monodisperse. Moreover, multiple droplet interactions are likely to be very important. Thus, a need to understand the critical cone angle and thereby the critical electric field in the interaction of (i) two unequal sized droplets, and (ii) interaction between three or more droplets aligned collinearly with the electric field, is expected to be quite relevant. It is therefore necessary to extend the analysis for two equal sized droplets to multiple droplets of unequal sizes.
Although quite a few numerical, experimental and analytical studies have been conducted in the recent past to understand the physics of the behaviour of droplets under an electric field (Chen et al. Reference Chen, Liu, Qi, Wang, Liu and Kong2019; Lu et al. Reference Lu, Lu, Zhang and Tryggvason2019; Abbasi et al. Reference Abbasi, Song, Cho and Lee2020; Huang et al. Reference Huang, He, Luo, Xu, Lu and Yang2020a,Reference Huang, He, Luo, Xu, Lu and Yangb; Chirkov, Dobrovolskii & Vasilkov Reference Chirkov, Dobrovolskii and Vasilkov2021; Das & Saintillan Reference Das and Saintillan2021; Li et al. Reference Li, Dou, Yu, Li, Zhang, Xu, Sun, Wang and Wang2021b; Sorgentone et al. Reference Sorgentone, Kach, Khair, Walker and Vlahovska2021; Sorgentone & Vlahovska Reference Sorgentone and Vlahovska2021; Li et al. Reference Li, Dou, Yu, Huang, Zhang, Xu, Sun, Wang and Wang2021a; Ou et al. Reference Ou, Li, Jin, Chen, Ma and Gao2022) there have been very few studies which addressed the interaction of unequal sized droplets under a uniform electric field (Anand et al. Reference Anand, Roy, Naik, Juvekar and Thaokar2019).
As can be seen from table 1, the referred works do not really address the issue of smaller critical capillary number, seen for non-coalescence of two unequal sized droplets or three equal or unequal sized droplets, as compared with that of two equal sized droplets (which has been the simplest, and most commonly addressed, problem in the literature). In fact, none of the above works address the issue of the fate of the droplets after coalescence.
Table 1. Literature review.

The motivation of our work is really to explain an important question, relevant in industrial electrocoalescence. Why do water-in-oil emulsions tend to show chaining and non-coalescence at much smaller electric fields, and thereby a much lower critical capillary number, as compared with the predictions of two equal sized droplets? And towards this, the present study indicates that two unequal sized droplets have a lower critical capillary number. Similarly, a three equal or unequal sized droplet system also has a lower critical capillary number as compared with the critical capillary number of a two equal sized droplet system, the most commonly studied system in the literature.
It has been shown that a size difference between the droplets can lead to an interaction termed ‘cone–dimple interaction’, wherein the smaller of the two interacting droplets forms a cone at the adjacent poles of the droplets, while the bigger one forms a dimple. While substantial work has been done on equal sized, two droplet interactions, a thorough numerical, analytical and experimental study on the interaction of collinear multiple droplets, aligned in the direction of electric field, is lacking and will be the subject of this study.
Chaining in electrodesalters is observed when multiple droplets, on application of an electric field, approach each other and form long chains which hinder the process of coalescence that can lead to shorting of the electrodes, thereby leading to loss of efficiency of the process (Pearce Reference Pearce1954; Chen et al. Reference Chen, Mohammed, Bailey, Luckham and Taylor1994). The critical electrocapillary number, ![]() $Ca_{c} = R \epsilon _e E_o^2/\gamma$ (where,
$Ca_{c} = R \epsilon _e E_o^2/\gamma$ (where, ![]() $R$ is the radius of the drop,
$R$ is the radius of the drop, ![]() $\epsilon _{e}$ is the electrical permittivity of the outer medium, the oil phase,
$\epsilon _{e}$ is the electrical permittivity of the outer medium, the oil phase, ![]() $\gamma$ is the interfacial tension and
$\gamma$ is the interfacial tension and ![]() $E_o$ is the applied electric field) at which non-coalescence is observed is found to be
$E_o$ is the applied electric field) at which non-coalescence is observed is found to be ![]() $0.06$ in theoretical studies and
$0.06$ in theoretical studies and ![]() $0.054$ in experiments (Anand et al. Reference Anand, Roy, Naik, Juvekar and Thaokar2019). However, the chaining of droplets leading to discontinuation of operation in desalters/electrocoalescers is found to occur at fields much smaller than one would expect from the critical capillary number observed in two equal sized droplets. It is therefore important to investigate if size asymmetry or multiple droplet interactions, lead to a reduction in the critical electrocapillary number. The present work tries to address these issues using experiments, analytical theory and boundary element calculations.
$0.054$ in experiments (Anand et al. Reference Anand, Roy, Naik, Juvekar and Thaokar2019). However, the chaining of droplets leading to discontinuation of operation in desalters/electrocoalescers is found to occur at fields much smaller than one would expect from the critical capillary number observed in two equal sized droplets. It is therefore important to investigate if size asymmetry or multiple droplet interactions, lead to a reduction in the critical electrocapillary number. The present work tries to address these issues using experiments, analytical theory and boundary element calculations.
2. Experiment
Silicone oil of viscosity 330 cSt (25 ![]() $^{\circ }$C) and density 970 (kg m
$^{\circ }$C) and density 970 (kg m![]() $^{-3}$) purchased from Sigma-Aldrich, was used without further purification. Deionized (DI) water of conductivity
$^{-3}$) purchased from Sigma-Aldrich, was used without further purification. Deionized (DI) water of conductivity ![]() $\sigma = 1.4 \times 10^{-4}\,{\rm S}\,{\rm m}^{-1}$ was obtained from EVOQUA Deionizer (Evoqua Water Technologies, Warrentdale). The interfacial tension of the silicone oil–water system, used in the study is
$\sigma = 1.4 \times 10^{-4}\,{\rm S}\,{\rm m}^{-1}$ was obtained from EVOQUA Deionizer (Evoqua Water Technologies, Warrentdale). The interfacial tension of the silicone oil–water system, used in the study is ![]() $23\,{\rm mN}\,{\rm m}^{-1}$ (Anand, Juvekar & Thaokar Reference Anand, Juvekar and Thaokar2020). The other physical parameters used in the experiments and simulation are reported in table 2 and table 3.
$23\,{\rm mN}\,{\rm m}^{-1}$ (Anand, Juvekar & Thaokar Reference Anand, Juvekar and Thaokar2020). The other physical parameters used in the experiments and simulation are reported in table 2 and table 3.
Table 2. Physical parameters of fluid used in experiments.
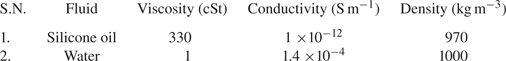
Table 3. Parameters used in numerical modelling.

Figure 1(a) shows the schematic diagram of the experimental set-up. The experimental set-up consisted of a rectangular cuvette (![]() $10\,{\rm mm} \times 10\,{\rm mm}$), where two parallel copper plate electrodes (
$10\,{\rm mm} \times 10\,{\rm mm}$), where two parallel copper plate electrodes (![]() $45\,{\rm mm} \times 10\,{\rm mm} \times 1.5\,{\rm mm}$) were fixed onto the opposite walls of the cuvette. The copper electrodes were connected to a high voltage amplifier (Trek, 20/20C). The voltage amplitude and the frequency (50 Hz) of the AC signal were adjusted with the help of a function generator (Agilent, 33220A). The cuvette was filled with silicone oil, wherein two or three DI water droplets were inserted with the help of a syringe. In the case of three droplets, the size of the central droplet varied in the range 100–200
$45\,{\rm mm} \times 10\,{\rm mm} \times 1.5\,{\rm mm}$) were fixed onto the opposite walls of the cuvette. The copper electrodes were connected to a high voltage amplifier (Trek, 20/20C). The voltage amplitude and the frequency (50 Hz) of the AC signal were adjusted with the help of a function generator (Agilent, 33220A). The cuvette was filled with silicone oil, wherein two or three DI water droplets were inserted with the help of a syringe. In the case of three droplets, the size of the central droplet varied in the range 100–200 ![]() $\mathrm {\mu }$m, whereas the size of the two adjacent droplets varied from 300 to 400
$\mathrm {\mu }$m, whereas the size of the two adjacent droplets varied from 300 to 400 ![]() $\mathrm {\mu }$m.
$\mathrm {\mu }$m.

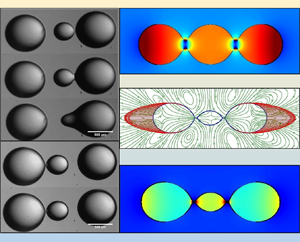
Figure 1. (a) Experimental set-up to study interactions of two or three aqueous droplets suspended in silicone oil. (b) (i) Three aqueous droplets undergoing coalescence: ![]() $Ca=0.024$, (ii) three aqueous droplets undergoing non-coalescence:
$Ca=0.024$, (ii) three aqueous droplets undergoing non-coalescence: ![]() $Ca=0.04$ (iii) two aqueous droplets undergoing non-coalescence:
$Ca=0.04$ (iii) two aqueous droplets undergoing non-coalescence: ![]() $Ca= 0.043$ and (iv) two aqueous droplets undergoing coalescence:
$Ca= 0.043$ and (iv) two aqueous droplets undergoing coalescence: ![]() $Ca = 0.044$. Scale bar is 500
$Ca = 0.044$. Scale bar is 500 ![]() $\mathrm {\mu }$m. Here, the radius ratio is
$\mathrm {\mu }$m. Here, the radius ratio is ![]() $\chi = R_{2}/R_{1}$.
$\chi = R_{2}/R_{1}$.
For capturing coalescence and non-coalescence interactions of the droplets, high-speed videography (5000–10 000 frames s![]() $^{-1}$) was conducted using a camera (Vision Research, Phantom v12). The camera was attached to a stereo zoom microscope (Nikon Instruments, model SMZ1000) to magnify the image. A fibre optics light source (Nikon, model: C-FI230) was used for providing sufficient light. The high-speed images were analysed using ImageJ. All the experiments were conducted at room temperature (25
$^{-1}$) was conducted using a camera (Vision Research, Phantom v12). The camera was attached to a stereo zoom microscope (Nikon Instruments, model SMZ1000) to magnify the image. A fibre optics light source (Nikon, model: C-FI230) was used for providing sufficient light. The high-speed images were analysed using ImageJ. All the experiments were conducted at room temperature (25 ![]() $^{\circ }$C).
$^{\circ }$C).
An earlier study on two drop interactions under an applied uniform electric field, (Anand et al. Reference Anand, Roy, Naik, Juvekar and Thaokar2019) showed that the cone angles, as well as the critical cone angle and the capillary numbers, are remarkably insensitive to the frequency of the applied field. The frequencies explored were in the range ![]() $\omega =50\unicode{x2013}5000\,{\rm Hz}$. Even for the highest frequency explored, the time period of the AC signal (0.2 ms) was at least one order higher than the Maxwell–Wagner relaxation time for the system
$\omega =50\unicode{x2013}5000\,{\rm Hz}$. Even for the highest frequency explored, the time period of the AC signal (0.2 ms) was at least one order higher than the Maxwell–Wagner relaxation time for the system ![]() $t_{MW} =({\epsilon _i +2 \epsilon _e})/({\sigma _i+2 \sigma _e})$, which is of the order of 0.02 ms for a deionized water–oil system. Here,
$t_{MW} =({\epsilon _i +2 \epsilon _e})/({\sigma _i+2 \sigma _e})$, which is of the order of 0.02 ms for a deionized water–oil system. Here, ![]() $\epsilon$ and
$\epsilon$ and ![]() $\sigma$ represent the permittivity and conductivity, and the subscripts are
$\sigma$ represent the permittivity and conductivity, and the subscripts are ![]() $i$ for droplet phase and
$i$ for droplet phase and ![]() $e$ for the external phase. Thus there is an instantaneous charge relaxation within a time period of the AC signal, thereby eliminating the possibility of the influence of frequency (in the
$e$ for the external phase. Thus there is an instantaneous charge relaxation within a time period of the AC signal, thereby eliminating the possibility of the influence of frequency (in the ![]() $\omega < 50\,000\,{\rm Hz}$ range) in the approach and pre-contact phases. In our current work the experiments were conducted at 50 Hz AC and this frequency was kept constant for all the experiments. Most electro-desalters that are used in refineries for breaking the water-in-oil emulsions typically employ AC fields with a frequency corresponding to the frequency of the voltage distributed in the power grids (which could be
$\omega < 50\,000\,{\rm Hz}$ range) in the approach and pre-contact phases. In our current work the experiments were conducted at 50 Hz AC and this frequency was kept constant for all the experiments. Most electro-desalters that are used in refineries for breaking the water-in-oil emulsions typically employ AC fields with a frequency corresponding to the frequency of the voltage distributed in the power grids (which could be ![]() $50$ or
$50$ or ![]() $60\ {\rm Hz}$); AC fields offer an advantage over DC fields by suppressing electrophoretic motion thereby enabling systematic experiments and preventing electrode-to-electrode oscillations. In figure 4, wherein numerical results are compared with experiments, a frequency of 50 Hz was used to simulate experimental conditions in a perfectly conducting perfect dielectric set-up. The rest of the numerical results were obtained by applying a DC electric field to study deformations and cone angles since the frequency is expected not to be an important parameter.
$60\ {\rm Hz}$); AC fields offer an advantage over DC fields by suppressing electrophoretic motion thereby enabling systematic experiments and preventing electrode-to-electrode oscillations. In figure 4, wherein numerical results are compared with experiments, a frequency of 50 Hz was used to simulate experimental conditions in a perfectly conducting perfect dielectric set-up. The rest of the numerical results were obtained by applying a DC electric field to study deformations and cone angles since the frequency is expected not to be an important parameter.
3. Numerical method
Two or three uncharged droplets of an infinitely conducting fluid having radii ![]() $R_1$,
$R_1$, ![]() $R_2$ and
$R_2$ and ![]() $R_3$, and suspended in a non-conducting medium are considered. Here,
$R_3$, and suspended in a non-conducting medium are considered. Here, ![]() $R_1$ and
$R_1$ and ![]() $R_3$ are kept equal while
$R_3$ are kept equal while ![]() $R_2 \leqslant R_1$. The droplets are aligned along the direction of the applied electric field (
$R_2 \leqslant R_1$. The droplets are aligned along the direction of the applied electric field (![]() ${\tilde {\boldsymbol E}_0}= E_0 {\boldsymbol e_z}$), as shown in figure 2(a). The non-dimensional field is given by
${\tilde {\boldsymbol E}_0}= E_0 {\boldsymbol e_z}$), as shown in figure 2(a). The non-dimensional field is given by ![]() $e_z$. In the three droplet system, we refer to the middle droplet as the central droplet, and both perfect geometry-centric and off-centric positions of the central droplet have been considered in this work. The two poles of the two droplets which face each other are termed the ‘adjacent poles’, whereas the other two poles are termed the ‘distant poles’.
$e_z$. In the three droplet system, we refer to the middle droplet as the central droplet, and both perfect geometry-centric and off-centric positions of the central droplet have been considered in this work. The two poles of the two droplets which face each other are termed the ‘adjacent poles’, whereas the other two poles are termed the ‘distant poles’.

Figure 2. Schematic for (a) droplets under electric field and (b) the Bird et al. (Reference Bird, Ristenpart, Belmonte and Stone2009) model modified to analytically solve for asymmetric cone formation with two cone angles ![]() $\beta _1$ and
$\beta _1$ and ![]() $\beta _2$.
$\beta _2$.
The parameters used to characterize the system are the viscosity ratio (![]() $\lambda =\mu _i/\mu _e$), permittivity ratio (
$\lambda =\mu _i/\mu _e$), permittivity ratio (![]() $Q=\epsilon _i / \epsilon _e$), conductivity ratio (
$Q=\epsilon _i / \epsilon _e$), conductivity ratio (![]() $\sigma _r =\sigma _e / \sigma _i$) and the electrocapillary number (
$\sigma _r =\sigma _e / \sigma _i$) and the electrocapillary number (![]() $Ca={R_1 \epsilon _0 \epsilon _e E_0^2}/{\gamma }$), where
$Ca={R_1 \epsilon _0 \epsilon _e E_0^2}/{\gamma }$), where ![]() $i$ and
$i$ and ![]() $e$ are the droplet and medium phases, respectively. Taylor's leaky dielectric theory is used to model the system and the perfectly conducting droplet in a perfectly dielectric medium is realized using
$e$ are the droplet and medium phases, respectively. Taylor's leaky dielectric theory is used to model the system and the perfectly conducting droplet in a perfectly dielectric medium is realized using ![]() $\sigma _r =0.001$ in a leaky dielectric formalism. We present quantities in their non-dimensional form, the electric field non-dimensionalized by the magnitude of the applied field
$\sigma _r =0.001$ in a leaky dielectric formalism. We present quantities in their non-dimensional form, the electric field non-dimensionalized by the magnitude of the applied field ![]() $E_o$, the electric potentials by
$E_o$, the electric potentials by ![]() $E_o R_1$, the distances by
$E_o R_1$, the distances by ![]() $R_1$, the size of the bigger droplet, the time by
$R_1$, the size of the bigger droplet, the time by ![]() $\mu _e/\epsilon _e E_o^2$, the velocities by
$\mu _e/\epsilon _e E_o^2$, the velocities by ![]() $R_1 \epsilon _e E_o^2/\mu _e$ and the stresses by
$R_1 \epsilon _e E_o^2/\mu _e$ and the stresses by ![]() $\epsilon _e E_o^2$. The electric field and potentials are given by
$\epsilon _e E_o^2$. The electric field and potentials are given by
where ![]() $\phi$ is the electric potential.
$\phi$ is the electric potential.
The boundary conditions at the fluid interfaces are
Here, ![]() $\boldsymbol {n}$ and
$\boldsymbol {n}$ and ![]() $\boldsymbol {t}$ are the outward unit normal and unit tangent, respectively. The Maxwell stress tensor at the interface is given by
$\boldsymbol {t}$ are the outward unit normal and unit tangent, respectively. The Maxwell stress tensor at the interface is given by
The fluid velocity ![]() $\textbf {u}$ is given by the Stokes and continuity equations as
$\textbf {u}$ is given by the Stokes and continuity equations as
where ![]() $p$ is the pressure and
$p$ is the pressure and ![]() $\boldsymbol {\tau ^H}$ is the hydrodynamic stress. At the interface, continuity of velocity is applicable. The interfacial tension balances the stress jump and is written as
$\boldsymbol {\tau ^H}$ is the hydrodynamic stress. At the interface, continuity of velocity is applicable. The interfacial tension balances the stress jump and is written as
where ![]() $\kappa =((\boldsymbol {I-nn})\boldsymbol{\cdot} \boldsymbol {\nabla })\boldsymbol{\cdot} \boldsymbol {n}$ is twice the mean curvature of the interface and
$\kappa =((\boldsymbol {I-nn})\boldsymbol{\cdot} \boldsymbol {\nabla })\boldsymbol{\cdot} \boldsymbol {n}$ is twice the mean curvature of the interface and ![]() $[[\,\cdot\,]]$ denotes the stress jump across the interface of the droplet. The system is assumed to be axisymmetric and calculations are carried out on one half of the one-dimensional arc discretized into
$[[\,\cdot\,]]$ denotes the stress jump across the interface of the droplet. The system is assumed to be axisymmetric and calculations are carried out on one half of the one-dimensional arc discretized into ![]() $N$ elements. The arclength (
$N$ elements. The arclength (![]() $c$) is used for parameter representation, and the node points are described in a cylindrical coordinate system by cubic spline interpolation.
$c$) is used for parameter representation, and the node points are described in a cylindrical coordinate system by cubic spline interpolation.
The normal electric field is calculated using the following integral equation (Sherwood Reference Sherwood1988; Baygents, Rivette & Stone Reference Baygents, Rivette and Stone1998):
 \begin{align} E_{ne}(\boldsymbol{x_0})=\frac{2}{1+\sigma_r}\boldsymbol{n(x_0)}\boldsymbol{\cdot} \boldsymbol{{e_z}}+\frac{1-\sigma_r}{2{\rm \pi} (1+\sigma_r)} \boldsymbol{n(x_0)}\boldsymbol{\cdot} \sum_{i=1}^{2,3} \int_{\zeta_i} \frac{\boldsymbol{x_0-x}}{\boldsymbol{(|x_0-x|)^3}} E_{ni}(\boldsymbol{x}) \,{\rm d}c(\boldsymbol{x}), \end{align}
\begin{align} E_{ne}(\boldsymbol{x_0})=\frac{2}{1+\sigma_r}\boldsymbol{n(x_0)}\boldsymbol{\cdot} \boldsymbol{{e_z}}+\frac{1-\sigma_r}{2{\rm \pi} (1+\sigma_r)} \boldsymbol{n(x_0)}\boldsymbol{\cdot} \sum_{i=1}^{2,3} \int_{\zeta_i} \frac{\boldsymbol{x_0-x}}{\boldsymbol{(|x_0-x|)^3}} E_{ni}(\boldsymbol{x}) \,{\rm d}c(\boldsymbol{x}), \end{align}
where ![]() $\boldsymbol {x_0,x}$ are the position vectors of the observation and force singularity points on the interface. Here,
$\boldsymbol {x_0,x}$ are the position vectors of the observation and force singularity points on the interface. Here, ![]() $\zeta _i$ is the arclength for the droplets 1 and 2 or 1, 2 and 3 for the 2 and 3 droplet cases. Knowing the normal electric field, the potential is given by
$\zeta _i$ is the arclength for the droplets 1 and 2 or 1, 2 and 3 for the 2 and 3 droplet cases. Knowing the normal electric field, the potential is given by
 \begin{equation} \phi(\boldsymbol{x_0})=\phi_{o}(\boldsymbol{x_0})-\left(\frac{1-\sigma_r}{4{\rm \pi}}\right) \sum_{i=1}^{2,3}\int_{\zeta_i} \frac{E_{ni}(\boldsymbol{x})}{|\boldsymbol{x_0-x}|}\, {\rm d}c(\boldsymbol{x}), \end{equation}
\begin{equation} \phi(\boldsymbol{x_0})=\phi_{o}(\boldsymbol{x_0})-\left(\frac{1-\sigma_r}{4{\rm \pi}}\right) \sum_{i=1}^{2,3}\int_{\zeta_i} \frac{E_{ni}(\boldsymbol{x})}{|\boldsymbol{x_0-x}|}\, {\rm d}c(\boldsymbol{x}), \end{equation}
where ![]() $\phi _{o}(x_0)=-z$ is the applied potential.
$\phi _{o}(x_0)=-z$ is the applied potential.
The instantaneous distribution of non-dimensional velocity over the interface at any point ![]() $\boldsymbol {x_0}$ is given by the Fredholm integral equation of second kind (Pozrikidis Reference Pozrikidis1992, Reference Pozrikidis2001)
$\boldsymbol {x_0}$ is given by the Fredholm integral equation of second kind (Pozrikidis Reference Pozrikidis1992, Reference Pozrikidis2001)
 $$\begin{align} \boldsymbol{u_o(x_0)}&={-}\frac{1}{4{\rm \pi} (1+\lambda)} \sum_{i=1}^{2,3} \int_{\zeta_i} \boldsymbol{\Delta f(x)\boldsymbol{\cdot} G(x,x_0)} \,{\rm d}c(\boldsymbol{x})\nonumber\\ &\quad+\frac{1-\lambda}{4{\rm \pi} (1+\lambda)} \sum_{i=1}^{2,3} \int_{\zeta_i}^{PV} \boldsymbol{n(x)}\boldsymbol{\cdot} \boldsymbol{T(x,x_0)}\boldsymbol{\cdot} \boldsymbol{u(x)} \,{\rm d}c(\boldsymbol{x}), \end{align}$$
$$\begin{align} \boldsymbol{u_o(x_0)}&={-}\frac{1}{4{\rm \pi} (1+\lambda)} \sum_{i=1}^{2,3} \int_{\zeta_i} \boldsymbol{\Delta f(x)\boldsymbol{\cdot} G(x,x_0)} \,{\rm d}c(\boldsymbol{x})\nonumber\\ &\quad+\frac{1-\lambda}{4{\rm \pi} (1+\lambda)} \sum_{i=1}^{2,3} \int_{\zeta_i}^{PV} \boldsymbol{n(x)}\boldsymbol{\cdot} \boldsymbol{T(x,x_0)}\boldsymbol{\cdot} \boldsymbol{u(x)} \,{\rm d}c(\boldsymbol{x}), \end{align}$$
where ![]() $PV$ is the principal value integral pertaining to the droplet over which integration is carried out and G and T are known kernels of the velocity and stress field, respectively. The electric stress jump at the interface is given by (3.6), where
$PV$ is the principal value integral pertaining to the droplet over which integration is carried out and G and T are known kernels of the velocity and stress field, respectively. The electric stress jump at the interface is given by (3.6), where
Once the instantaneous velocity for every node point is known, the interface is temporally advanced using the explicit Euler scheme for each time step ![]() $\delta t$
$\delta t$
The change in volume was also computed for all our simulations and it was noted that the value always remained below ![]() $0.5\,\%$. The simulations were continued until the droplets contact. In post-contact phase, bridge models numerically obtained from a modified analytical theory are stitched to bridge the off-centric two or three droplets. The BEM formalism, which is explained and used in Roy & Thaokar (Reference Roy and Thaokar2020), is adopted to further simulate the droplets until coalescence or non-coalescence is achieved. Thus, the entire simulation is conducted discontinuously in two steps.
$0.5\,\%$. The simulations were continued until the droplets contact. In post-contact phase, bridge models numerically obtained from a modified analytical theory are stitched to bridge the off-centric two or three droplets. The BEM formalism, which is explained and used in Roy & Thaokar (Reference Roy and Thaokar2020), is adopted to further simulate the droplets until coalescence or non-coalescence is achieved. Thus, the entire simulation is conducted discontinuously in two steps.
4. Results and discussions
The dynamics of two and three droplet systems, equal and unequal in size, in an externally applied uniform electric field is divided into three phases. The first phase is the approach phase that starts from the time the field is applied to the droplets, to the point where cones are formed at the poles adjacent to each other. This is followed by a contact between these cones formed at the two approaching poles of the droplets. Lastly, in the post-contact phase, a bridge is formed at contact which eventually leads to coalescence or non-coalescence of the droplets.
4.1. The main experimental observation
Three DI water droplets were suspended in silicone oil, collinear to each other, aligned in the direction of the applied electric field (figure 1a (i), (ii)). The droplets on either side were similar in diameter while the droplet at the centre was smaller than the other two. A slight off-centric location of the central droplet led to an asymmetric contact of the central droplet under an applied electric field. The central droplet moved towards either the left or to the right droplet (depending upon its initial position) and an asymmetric double cone structure was observed between the droplets at contact. A bridge was formed between the contacting droplets, which either grew and showed coalescence for low electric fields or snapped and exhibited non-coalescence for high electric fields. In a similar way, in the two droplet system, a cone–cone contact was observed and the outcome could be either coalescence or non-coalescence (figure 1b (iii), (iv)) of the droplets in concurrence with our earlier reported study (Anand et al. Reference Anand, Roy, Naik, Juvekar and Thaokar2019; Roy et al. Reference Roy, Anand and Thaokar2019).
For a pair of equal sized droplets suspended in silicone oil and subjected to a uniform electric field, the experimentally observed critical ![]() $Ca$ is (
$Ca$ is (![]() $Ca_c$)
$Ca_c$) ![]() $\sim 0.054$, at which a transition from coalescence to non-coalescence of the droplets occurs (Anand et al. Reference Anand, Roy, Naik, Juvekar and Thaokar2019). However, such a systematic study has not been reported for two unequal sized droplets. Therefore, several experiments were conducted with two unequal sized droplets under an electric field and the outcomes on contact of these droplets are plotted in figure 3. Similarly, such studies have not been conducted for a three droplet system either, and are also presented in figure 3, which shows the coalescence or non-coalescence outcomes of two and three equal and unequal sized droplets under a uniform external electric field. These experimental data are presented on a phase diagram with
$\sim 0.054$, at which a transition from coalescence to non-coalescence of the droplets occurs (Anand et al. Reference Anand, Roy, Naik, Juvekar and Thaokar2019). However, such a systematic study has not been reported for two unequal sized droplets. Therefore, several experiments were conducted with two unequal sized droplets under an electric field and the outcomes on contact of these droplets are plotted in figure 3. Similarly, such studies have not been conducted for a three droplet system either, and are also presented in figure 3, which shows the coalescence or non-coalescence outcomes of two and three equal and unequal sized droplets under a uniform external electric field. These experimental data are presented on a phase diagram with ![]() $Ca$ and the radius ratio
$Ca$ and the radius ratio ![]() $\chi$ as the axes. Here,
$\chi$ as the axes. Here, ![]() $Ca$ is based on the radius of the bigger droplet. The radius ratio
$Ca$ is based on the radius of the bigger droplet. The radius ratio ![]() $\chi =R_1/R_2$ is defined as the ratio of the radius of the smaller droplet to that of the bigger droplet. A phase boundary is observed between the coalescence and non-coalescence regimes. It is observed that the critical capillary number shows a systematic decrease from a value of
$\chi =R_1/R_2$ is defined as the ratio of the radius of the smaller droplet to that of the bigger droplet. A phase boundary is observed between the coalescence and non-coalescence regimes. It is observed that the critical capillary number shows a systematic decrease from a value of ![]() $0.054$ for two equal sized droplets, to much lower values as the ratio of the droplet size is reduced in the two droplet system. Figure 3 also shows that the critical capillary number is around
$0.054$ for two equal sized droplets, to much lower values as the ratio of the droplet size is reduced in the two droplet system. Figure 3 also shows that the critical capillary number is around ![]() $0.03$ for the system of three equal sized droplets, much smaller than
$0.03$ for the system of three equal sized droplets, much smaller than ![]() $Ca_c\sim 0.06$ for the system of two equal sized droplets. This critical capillary number further reduces when the radius ratio decreases, that is, when the radius of the droplet at the centre is smaller than the two adjacent droplets. The sensitivity of
$Ca_c\sim 0.06$ for the system of two equal sized droplets. This critical capillary number further reduces when the radius ratio decreases, that is, when the radius of the droplet at the centre is smaller than the two adjacent droplets. The sensitivity of ![]() $Ca_c$ to the radius ratio, as seen in experiments, is much greater for the two droplet system as compared with the three droplet system.
$Ca_c$ to the radius ratio, as seen in experiments, is much greater for the two droplet system as compared with the three droplet system.

Figure 3. Variation of ![]() $Ca$ with radius ratio (
$Ca$ with radius ratio (![]() $\chi = R_2/R_1$) for both two droplet and three droplet systems.
$\chi = R_2/R_1$) for both two droplet and three droplet systems.
Explaining these observations, namely the reduction in ![]() $Ca_c$ with radius ratio for the two droplet system and reduction in
$Ca_c$ with radius ratio for the two droplet system and reduction in ![]() $Ca_c$ in the three droplet system, for both equal and unequal sized droplets, forms the objective of this work. These findings are consistent with the typical observation in electrocoalescence of water-in-oil emulsions that the field required for effective dehydration is of the order of
$Ca_c$ in the three droplet system, for both equal and unequal sized droplets, forms the objective of this work. These findings are consistent with the typical observation in electrocoalescence of water-in-oil emulsions that the field required for effective dehydration is of the order of ![]() $1\,{\rm kV}\,{\rm cm}^{-1}$. Any field higher than this leads to chaining and electric sparks, thereby prohibiting any further increase of field. If one considers that droplets grow to
$1\,{\rm kV}\,{\rm cm}^{-1}$. Any field higher than this leads to chaining and electric sparks, thereby prohibiting any further increase of field. If one considers that droplets grow to ![]() $800\,\mathrm {\mu }{\rm m}$ in emulsion dehydration, this results in a critical capillary number
$800\,\mathrm {\mu }{\rm m}$ in emulsion dehydration, this results in a critical capillary number ![]() $Ca_c=0.005$ for typical interfacial tension values of 30 mN m−1. This is almost 10 times lower than the theoretical value of
$Ca_c=0.005$ for typical interfacial tension values of 30 mN m−1. This is almost 10 times lower than the theoretical value of ![]() $Ca_c=0.06$ or experimental value of
$Ca_c=0.06$ or experimental value of ![]() $Ca_c=0.054$ for a two droplet system. The two and three droplet experimental results in figure 3 indicate a trend of reduction of
$Ca_c=0.054$ for a two droplet system. The two and three droplet experimental results in figure 3 indicate a trend of reduction of ![]() $Ca_c$ with the radius ratio
$Ca_c$ with the radius ratio ![]() $\chi$, which could possibly explain the lower critical capillary numbers observed in electrocoalescence of polydisperse emulsions.
$\chi$, which could possibly explain the lower critical capillary numbers observed in electrocoalescence of polydisperse emulsions.
4.2. Analytical theory and numerical calculations to understand the mechanism
Numerical simulations using the boundary element method were carried out to predict the simultaneous translation and deformation of the droplets in two and three droplet systems. For example, in the three droplet system, the movement of the slightly off-centred central droplet towards its neighbours was calculated using BEM and compared with experiments. It was observed that BEM calculations, qualitatively as well as quantitatively and to quite an extent, agree with the asymmetric contact seen in experiments (figure 4). It should be noted that the initial conditions for the simulations were taken from the experimental pictures, and no other fitting parameter was used (figure 4).

Figure 4. (a) Experimental (BEM superimposed) and (b) BEM prediction for DI water droplet in silicone oil at time ![]() $t = 0$ and at time t = contact, for (i)
$t = 0$ and at time t = contact, for (i) ![]() $Ca=0.033$, (ii)
$Ca=0.033$, (ii) ![]() $Ca = 0.036$ and (iii)
$Ca = 0.036$ and (iii) ![]() $Ca = 0.038$. (c) Numerically and experimentally obtained variation of separation distance with time for a three droplet system under an electric field with
$Ca = 0.038$. (c) Numerically and experimentally obtained variation of separation distance with time for a three droplet system under an electric field with ![]() $Ca=0.036$ and
$Ca=0.036$ and ![]() $R_2/R_1 = 0.51$.
$R_2/R_1 = 0.51$.
The coalescence and non-coalescence phenomena critically depend upon the cone angle formed at the adjacent poles, in two and three droplet systems (Anand et al. Reference Anand, Roy, Naik, Juvekar and Thaokar2019). The cone angle at the poles is a balance of electric, capillary stresses and hydrodynamic stresses. A systematic analysis of electric field at the poles, the deformation and cone angle at the interacting poles was therefore undertaken.
Figure 5 shows a schematic of a three drop system at the points of contact. Symmetric deformation was estimated by ![]() $D=({P+Q-2M})/({P+Q+2M})$ and asymmetric deformation was estimated by
$D=({P+Q-2M})/({P+Q+2M})$ and asymmetric deformation was estimated by ![]() $AD={P}/{Q}-1$. A similar exercise was adopted for two drop interaction as well.
$AD={P}/{Q}-1$. A similar exercise was adopted for two drop interaction as well.

Figure 5. Estimation of symmetric and asymmetric deformation.
4.2.1. Two droplet system
The details of the analytical theory in the small deformation limit are presented in the supplementary material available at https://doi.org/10.1017/jfm.2022.925. The analytical results agree with those of Sorgentone et al. (Reference Sorgentone, Kach, Khair, Walker and Vlahovska2021) but differ from Zabarankin (Reference Zabarankin2020). While electric interactions between the droplets, as well as shape–translation coupling, is taken into account in the analytical theory, the hydrodynamic interactions are neglected. Thus the hydrodynamics is solved over an isolated droplet subject to a uniform electric field. Electrohydrodynamic flows due to tangential electric stresses are absent in perfect conductor drops in a perfect dielectric medium. Therefore hydrodynamic interactions are not expected to be important (Sorgentone et al. Reference Sorgentone, Kach, Khair, Walker and Vlahovska2021; Sorgentone & Vlahovska Reference Sorgentone and Vlahovska2021).
Analytical results (equation (14) of the supplementary material)
indicate that the time of contact of the droplets increases as the ratio of radii, ![]() $\chi =R_2/R_1$ decreases, essentially because the reduction in the electrostatic force of attraction is much smaller
$\chi =R_2/R_1$ decreases, essentially because the reduction in the electrostatic force of attraction is much smaller ![]() $\sim \chi ^3$ than the reduction in the drag on the smaller droplet
$\sim \chi ^3$ than the reduction in the drag on the smaller droplet ![]() $\sim \chi$. (Note, the time of contact is obtained by putting d
$\sim \chi$. (Note, the time of contact is obtained by putting d ![]() $(t)=1+\chi$.)
$(t)=1+\chi$.)
The analytical theory suggests that the electric field experienced by the smaller droplet remains unchanged with a decrease in ![]() $\chi$. However, the electric field in the bigger droplet decreases as
$\chi$. However, the electric field in the bigger droplet decreases as ![]() $\chi ^3$ as the radius ratio
$\chi ^3$ as the radius ratio ![]() $\chi$ decreases (equations (10) and (11) of the supplementary material). This is essentially because the unperturbed electric field is equal to
$\chi$ decreases (equations (10) and (11) of the supplementary material). This is essentially because the unperturbed electric field is equal to ![]() $3$ (non-dimensional) in both the smaller and bigger droplets, independent of their size. When the droplets interact, the disturbance electric field due to the bigger droplet, which is experienced by the smaller droplet, scales as
$3$ (non-dimensional) in both the smaller and bigger droplets, independent of their size. When the droplets interact, the disturbance electric field due to the bigger droplet, which is experienced by the smaller droplet, scales as ![]() $R_1^3$. Thus the non-dimensional electric field experienced by the smaller droplet scales as
$R_1^3$. Thus the non-dimensional electric field experienced by the smaller droplet scales as ![]() $3+6/d^3$. On the other hand, the field on the bigger droplet scales as
$3+6/d^3$. On the other hand, the field on the bigger droplet scales as ![]() $3 +6 \chi ^3/d^3$, and therefore reduces as
$3 +6 \chi ^3/d^3$, and therefore reduces as ![]() $\chi$ decreases. This is indeed seen in simulations as well (figure 6), at very short times.
$\chi$ decreases. This is indeed seen in simulations as well (figure 6), at very short times.

Figure 6. Numerically obtained variation of non-dimensional electric field at the adjacent poles (![]() $E_{n}^{p}$) for two droplet system with non-dimensional time (
$E_{n}^{p}$) for two droplet system with non-dimensional time (![]() $t$). (Inset: closer look at variation of electric field from time
$t$). (Inset: closer look at variation of electric field from time ![]() $t=0.01$ to
$t=0.01$ to ![]() $t=5$.)
$t=5$.)
However, as the time progresses, very soon, the electric field in the bigger droplet, as seen in simulations, becomes greater than that in the smaller droplet (figure 6). The small deformation theory, which predicts that the smaller droplet continues to experience a greater electric field throughout the temporal evolution, fails at this point (refer to supplementary material (figure 3a of supplementary material)). To understand the transition of the electric field in the bigger droplet from being smaller to greater than that of the smaller droplet, a careful investigation of simultaneous deformation and development of the electric field at the poles of the droplets is undertaken.
For any given ratio, ![]() $\chi$, the analytical theory predicts that the deformation of the smaller droplet is smaller than the bigger droplet. This is because the size and hence the effective capillary number of the smaller droplet is smaller. The off-centric deformation (
$\chi$, the analytical theory predicts that the deformation of the smaller droplet is smaller than the bigger droplet. This is because the size and hence the effective capillary number of the smaller droplet is smaller. The off-centric deformation (![]() $AD$) of the smaller droplet is same as that of the bigger droplet. However, this value of
$AD$) of the smaller droplet is same as that of the bigger droplet. However, this value of ![]() $AD$ decreases as the
$AD$ decreases as the ![]() $\chi$ decreases. Thus, within the realm of far field linear theory, the smaller droplet seems to deform less for any given
$\chi$ decreases. Thus, within the realm of far field linear theory, the smaller droplet seems to deform less for any given ![]() $\chi$ (equations (24) and (25) of the supplementary material). The smaller deformations predicted by the analytical theory for the smaller droplet as compared with greater deformations for the bigger droplet are indeed seen in simulations as well (figure 7). This deformation of the bigger droplet continues to be greater than the smaller droplet (figure 7) in agreement with theory (refer to supplementary material (figure 4 of supplementary material)). One can conjecture that the greater deformability of the bigger droplet can lead to greater curvatures and thereby greater accumulation of charge and thereby electric field at the pole of the bigger droplet, explaining the development of greater electric field at the adjacent pole of the bigger droplet at short times and the cross-over from the field being lower in the smaller droplets to being greater in the smaller droplets (figure 6).
$\chi$ (equations (24) and (25) of the supplementary material). The smaller deformations predicted by the analytical theory for the smaller droplet as compared with greater deformations for the bigger droplet are indeed seen in simulations as well (figure 7). This deformation of the bigger droplet continues to be greater than the smaller droplet (figure 7) in agreement with theory (refer to supplementary material (figure 4 of supplementary material)). One can conjecture that the greater deformability of the bigger droplet can lead to greater curvatures and thereby greater accumulation of charge and thereby electric field at the pole of the bigger droplet, explaining the development of greater electric field at the adjacent pole of the bigger droplet at short times and the cross-over from the field being lower in the smaller droplets to being greater in the smaller droplets (figure 6).

Figure 7. (a) Numerically obtained variation of symmetric deformation, (![]() $D$) of individual droplets under electric field with non-dimensional time (
$D$) of individual droplets under electric field with non-dimensional time (![]() $t$) in two droplet system. (b) Numerically obtained variation of asymmetric deformation, (
$t$) in two droplet system. (b) Numerically obtained variation of asymmetric deformation, (![]() $AD$) of individual droplets under electric field with non-dimensional time in two droplet system.
$AD$) of individual droplets under electric field with non-dimensional time in two droplet system.
In line with the electric field in the smaller droplet changing from being greater than that in the bigger droplet at small times to being smaller than that in the bigger droplet at intermediate times, the cone angle at the smaller droplet, that represents local deformability, also shows a similar transition. The cone angle at the smaller droplet is greater than that of the bigger droplet at short times, and then shows a transition whereafter it is slightly smaller than the cone angle of the bigger droplet (figure 8).

Figure 8. Numerically obtained variation of cone angles at contact with non-dimensional time (![]() $t$) for two droplet system under electric field where
$t$) for two droplet system under electric field where ![]() $\beta _1$ and
$\beta _1$ and ![]() $\beta _2$ are the angles subtended by droplet 1 and droplet 2, respectively.
$\beta _2$ are the angles subtended by droplet 1 and droplet 2, respectively.
As the droplets further approach each other, and are near contact, a dramatic cross-over is observed, wherein the electric field at the bigger droplet now becomes lower than that at the smaller droplet (figure 6). This coincides with a remarkable increase in the deformation of the smaller droplet. Simultaneously, the cone angle of the smaller droplet becomes greater than that of the bigger droplet (figures 7 and 8). This can be explained by the observation that, as the two droplets approach and are near contact, the lubrication pressure in the intervening thin film increases. At this point, as the two droplets push against each other, the conical deformation in the bigger droplet (that is more deformable) is retarded, thereby reducing the growth of its local curvature at the pole. This also decreases the rate of increase of its electric field, and thereby its deformation and cone angle are also reduced. Simultaneously, the deformation, the electric field and the cone angle at the smaller droplet increase and exceed those on the bigger droplet. To summarize, at contact, for any given ![]() $\chi$, the cone angle at the smaller droplet is greater, and so is the electric field at its pole.
$\chi$, the cone angle at the smaller droplet is greater, and so is the electric field at its pole.
The more important question is whether this cone angle at the smaller droplet at contact increases or decreases with ![]() $\chi$. It is observed that, at short to intermediate times after application of the electric field, indeed the deformation, the electric field and the cone angle in the smaller droplet decrease as
$\chi$. It is observed that, at short to intermediate times after application of the electric field, indeed the deformation, the electric field and the cone angle in the smaller droplet decrease as ![]() $\chi$ decreases, in accordance with the linear theory. However, towards the end of the process, that is, near contact, when the mechanism of lubrication pressure induced deformation sets in, it appears that, as
$\chi$ decreases, in accordance with the linear theory. However, towards the end of the process, that is, near contact, when the mechanism of lubrication pressure induced deformation sets in, it appears that, as ![]() $\chi$ decreases, the smaller droplet is able to deform more and push itself into the bigger droplet, and thereby subtend a higher cone angle. This only becomes stronger as the droplet size decreases, because the relative size difference between the two droplets is greater. The smaller cone angle in the larger droplet at
$\chi$ decreases, the smaller droplet is able to deform more and push itself into the bigger droplet, and thereby subtend a higher cone angle. This only becomes stronger as the droplet size decreases, because the relative size difference between the two droplets is greater. The smaller cone angle in the larger droplet at ![]() $t=0$ is a consequence of inter-droplet interaction, even at
$t=0$ is a consequence of inter-droplet interaction, even at ![]() $t=0$, due to the small initial separation between the droplets. To explain this in another way, if the two droplets were of the same size, neither would be pushed back at near contact, and the rate of increase of cone angle of the two similarly sized droplets would be more moderate (figures 6–8).
$t=0$, due to the small initial separation between the droplets. To explain this in another way, if the two droplets were of the same size, neither would be pushed back at near contact, and the rate of increase of cone angle of the two similarly sized droplets would be more moderate (figures 6–8).
Thus, unlike the predications of the linear theory, two nonlinear phenomena seem to be at play. Firstly, the higher deformability of the bigger droplet initially results in the bigger droplet experiencing a greater electric field. Secondly, near contact, the greater deformability of the bigger droplet results in the smaller droplet admitting a greater electric field and cone angle. Thus, the end result is a consequence of great nonlinearity in the system. The cone angle in the smaller droplet at contact is greater than the bigger droplet, and this cone angle increases as ![]() $\chi$ decreases. This ultimately results in a smaller critical capillary number with a reduction in
$\chi$ decreases. This ultimately results in a smaller critical capillary number with a reduction in ![]() $\chi$. Therefore, the presence of smaller droplets in a polydisperse emulsion can lead to increased chaining and the results for two equal sized droplet system may be inaccurate.
$\chi$. Therefore, the presence of smaller droplets in a polydisperse emulsion can lead to increased chaining and the results for two equal sized droplet system may be inaccurate.
4.2.2. Three droplet system
The analytical theory for small deformations, presented in the supplementary material, considers a symmetric case, wherein the central droplet does not move, and the two droplets on either side are attracted to the inner droplet. Thus, the two droplets are considered at equal distances from the central droplet and are of the same size ![]() $R_3=R_1$.
$R_3=R_1$.
For ![]() $\chi =1$, the analytical theory suggests that the electric field in the central droplet is greater than the other two, and so are the deformation and cone angles. This can be seen in the simulations as well (figures 9–11). The trend is unchanged all the way up to contact of the droplets. The cone angle of the inner droplet is greater than that in the two droplet case with the same droplet size due to the stronger electric field experienced by the central droplet in the three droplet system. The effective capillary number experienced by the central droplet in the three droplet system is certainly higher than an equivalent two droplet system. In fact, in the case of a central droplet surrounded by
$\chi =1$, the analytical theory suggests that the electric field in the central droplet is greater than the other two, and so are the deformation and cone angles. This can be seen in the simulations as well (figures 9–11). The trend is unchanged all the way up to contact of the droplets. The cone angle of the inner droplet is greater than that in the two droplet case with the same droplet size due to the stronger electric field experienced by the central droplet in the three droplet system. The effective capillary number experienced by the central droplet in the three droplet system is certainly higher than an equivalent two droplet system. In fact, in the case of a central droplet surrounded by ![]() $n$ droplets on either side, a converged value of the enhanced electric field experienced by the inner droplet can be obtained, as shown in the supplementary material. This can partly explain the reduction in the critical electric field in a system of many droplets with the same size.
$n$ droplets on either side, a converged value of the enhanced electric field experienced by the inner droplet can be obtained, as shown in the supplementary material. This can partly explain the reduction in the critical electric field in a system of many droplets with the same size.

Figure 9. Numerically obtained variation of electric field at the adjacent poles (![]() $E_{n}^{p}$) for three droplet system with the non-dimensional time (
$E_{n}^{p}$) for three droplet system with the non-dimensional time (![]() $t$). (Inset: closer look at variation of electric field from time
$t$). (Inset: closer look at variation of electric field from time ![]() $t=0.01$ to
$t=0.01$ to ![]() $t=5$.)
$t=5$.)

Figure 10. (a) Numerically obtained variation of symmetric deformation (![]() $D$) of individual droplets under electric field with non-dimensional time (
$D$) of individual droplets under electric field with non-dimensional time (![]() $t$) in a three droplet system. (b) Numerically obtained variation of asymmetric deformation (
$t$) in a three droplet system. (b) Numerically obtained variation of asymmetric deformation (![]() $AD$) of individual droplets under electric field with non-dimensional time (
$AD$) of individual droplets under electric field with non-dimensional time (![]() $t$) in a three droplet system.
$t$) in a three droplet system.

Figure 11. Numerically obtained variation of cone angles at contact with non-dimensional time (![]() $t$) for three droplet system under an electric field where
$t$) for three droplet system under an electric field where ![]() $\beta _1$ and
$\beta _1$ and ![]() $\beta _2$ are the angles subtended by droplet 1 and droplet 2, respectively.
$\beta _2$ are the angles subtended by droplet 1 and droplet 2, respectively.
When ![]() $\chi <1$, and the central droplet is smaller than the other two, the behaviour is very similar to the two droplet case. Initially, the electric field of the central droplet is higher (in agreement with theory). However, as the droplets approach, the electric field of the outer droplet exceeds the inner droplet, possibly due to higher deformation of the outer droplets (figure 10). Finally, at contact, the smaller central droplet exhibits higher deformation due to a similar mechanism of higher intrusion of the cones of the smaller droplets into the bigger droplet. The cone angle too (figure 11) of the smaller inner droplet remains greater than the outer droplet at contact. The susceptibility to forming cones is also indicated in the asymmetric deformation plots (figure 10).
$\chi <1$, and the central droplet is smaller than the other two, the behaviour is very similar to the two droplet case. Initially, the electric field of the central droplet is higher (in agreement with theory). However, as the droplets approach, the electric field of the outer droplet exceeds the inner droplet, possibly due to higher deformation of the outer droplets (figure 10). Finally, at contact, the smaller central droplet exhibits higher deformation due to a similar mechanism of higher intrusion of the cones of the smaller droplets into the bigger droplet. The cone angle too (figure 11) of the smaller inner droplet remains greater than the outer droplet at contact. The susceptibility to forming cones is also indicated in the asymmetric deformation plots (figure 10).
4.3. Comparison between experiments and theory
The comparison of the separation between two droplets in the three droplet system vs time is shown in figure 4(c). The quantitative agreement between experiments and simulations is not very satisfactory and can be attributed to several factors, such as the effect of the conductivity of oil and inertial effects, amongst others, which are not accounted for in the model. The analytical theory was conducted by Sorgentone et al. (Reference Sorgentone, Kach, Khair, Walker and Vlahovska2021) and Zabarankin (Reference Zabarankin2020) and a similar exercise was conducted incorporating simultaneous shape changes, and is presented in the supplementary material.
A reasonable agreement is observed between the cone angles of the droplets as observed in experiments and computed in simulations. The comparison between the cone angles observed in experiments and predicted by BEM simulations is encouraging. The observations corroborate the hypothesis that, while at greater separations the cone angle in the bigger drop is greater, when the droplets contact, the cone angle in the smaller droplet exceeds that of the bigger droplet (figure 12).

Figure 12. Comparison of variation of numerically and experimentally obtained cone angles at the peak of AC voltage under electric field with time for three droplet and two droplet systems. (a) Three droplet system: ![]() $Ca=0.036$,
$Ca=0.036$, ![]() $R_2/R_1=0.51$. (b) Three droplet system:
$R_2/R_1=0.51$. (b) Three droplet system: ![]() $Ca=0.035$,
$Ca=0.035$, ![]() $R_2/R_1=0.43$. (c) Two droplet system:
$R_2/R_1=0.43$. (c) Two droplet system: ![]() $Ca=0.063$,
$Ca=0.063$, ![]() $R_2/R_1=0.7$.
$R_2/R_1=0.7$.
4.4. Post-contact phase
The analysis presented in the previous section indicates that the BEM calculations can be used to estimate the electric fields as well as the cone angles at the poles of the droplets. The cone angle at the poles of these droplets can be measured from the shape of the deformed droplets obtained in these simulations. In experiments, the two cones then contact, form a bridge and the pressure in the bridge determines whether the droplets coalesce or show non-coalescence. Experiments as well as simulations indicate that, in the case of a three droplet system, a slightly off-centre central droplet can lead to an asymmetric centre of mass motion of the central droplet, leading to contact with only one of the two outer droplets. Therefore, we consider the contact of two unequal sized droplets to analyse the bridge between the droplets.
The bridge formed between the droplets can be described by the formalism given by Bird et al. (Reference Bird, Ristenpart, Belmonte and Stone2009) for two equal sized droplets. The analytical model leads to the equation
 \begin{equation} \left(1+\tilde{r}'^2=\left(\frac{\tilde{r}}{k+\dfrac{pw}{2\gamma}\tilde{r}^2}\right)^2\right). \end{equation}
\begin{equation} \left(1+\tilde{r}'^2=\left(\frac{\tilde{r}}{k+\dfrac{pw}{2\gamma}\tilde{r}^2}\right)^2\right). \end{equation}
Here p, ![]() $\gamma$,
$\gamma$, ![]() $\tilde{r}$, w, k correspond to capillary pressure, surface tension, non-dimensional r, height and a constant respectively. The symmetry (equal size) of the two droplets is critical to the model. This symmetry leads to the two cone angles
$\tilde{r}$, w, k correspond to capillary pressure, surface tension, non-dimensional r, height and a constant respectively. The symmetry (equal size) of the two droplets is critical to the model. This symmetry leads to the two cone angles ![]() $\beta _1=\beta _2$.
$\beta _1=\beta _2$.
In the present case, however, the two droplets are unequal in size, clearly suggesting that ![]() $\beta _1\ne \beta _2$. Thus, the model of Bird et al. (Reference Bird, Ristenpart, Belmonte and Stone2009) has to be modified and solved to adjust for the asymmetric form of double cones with different boundary conditions for two different cone angles (
$\beta _1\ne \beta _2$. Thus, the model of Bird et al. (Reference Bird, Ristenpart, Belmonte and Stone2009) has to be modified and solved to adjust for the asymmetric form of double cones with different boundary conditions for two different cone angles (![]() $\beta _1$ and
$\beta _1$ and ![]() $\beta _2$) and a third parameter, the distance
$\beta _2$) and a third parameter, the distance ![]() $z_2$ (figure 2).
$z_2$ (figure 2).
The double cone volume ![]() $V$ (figure 13 is an exaggerated representation) is redistributed and conserved as the bridge is formed. Therefore, the neck surface area
$V$ (figure 13 is an exaggerated representation) is redistributed and conserved as the bridge is formed. Therefore, the neck surface area ![]() $S$ can be minimized. The energy functional
$S$ can be minimized. The energy functional ![]() $F=\gamma S - pV$ is considered, where
$F=\gamma S - pV$ is considered, where ![]() $p$ is the pressure inside the capillary, the surface area
$p$ is the pressure inside the capillary, the surface area ![]() $S=2{\rm \pi} r \sqrt {1+r'^2}\,{\rm d}z$ and the volume is given as
$S=2{\rm \pi} r \sqrt {1+r'^2}\,{\rm d}z$ and the volume is given as ![]() $V={\rm \pi} r^2\, {\rm d}z$. The resulting Euler–Lagrange equation leads to the differential equation
$V={\rm \pi} r^2\, {\rm d}z$. The resulting Euler–Lagrange equation leads to the differential equation
with boundary conditions changing to ![]() $r[-1]=\cot \beta _1$,
$r[-1]=\cot \beta _1$, ![]() $r[z_2]=\cot \beta _2$ and
$r[z_2]=\cot \beta _2$ and ![]() $\int _{-1}^{z_2}{\rm \pi} r^2 \,{\rm d}z=\tfrac {1}{3}\cot \beta _1^2+\tfrac {1}{3}\cot \beta _2^2$. Here,
$\int _{-1}^{z_2}{\rm \pi} r^2 \,{\rm d}z=\tfrac {1}{3}\cot \beta _1^2+\tfrac {1}{3}\cot \beta _2^2$. Here, ![]() $r$,
$r$, ![]() $z$ and
$z$ and ![]() $p$ are the coordinate axes and the bridge pressure, respectively.
$p$ are the coordinate axes and the bridge pressure, respectively.
The condition for coalescence or non-coalescence between two contacting droplets can be obtained by solving the above equation. The schematic for the problem is shown in figure 2. Since the parameters involved are ![]() $\beta _1$,
$\beta _1$, ![]() $\beta _2$ and
$\beta _2$ and ![]() $z_2$, one expects a plane of transition in these coordinates. For the bridge pressure
$z_2$, one expects a plane of transition in these coordinates. For the bridge pressure ![]() $p=0$, the phase separation plane obtained is shown in figure 14. The calculation procedure can be outlined as follows: to start with,
$p=0$, the phase separation plane obtained is shown in figure 14. The calculation procedure can be outlined as follows: to start with, ![]() $\beta _1$ is fixed to a value corresponding to experiments or simulations, and
$\beta _1$ is fixed to a value corresponding to experiments or simulations, and ![]() $p=0$ is assumed in the differential equation, for the plane of transition. An initial condition of
$p=0$ is assumed in the differential equation, for the plane of transition. An initial condition of ![]() $r(z_1=-1)=\beta _1$ is employed while a guess value of
$r(z_1=-1)=\beta _1$ is employed while a guess value of ![]() $r'(z_1=-1)$ is updated in an iterative manner. Also,
$r'(z_1=-1)$ is updated in an iterative manner. Also, ![]() $z_2$ is the other variable which is varied. The value of
$z_2$ is the other variable which is varied. The value of ![]() $\beta _2$ is fixed from experiments or simulations to analytically calculate the volume of the double cone to be used as a parameter to verify the solution. The equation is solved and the volume of the bridge is computed numerically. The numerically obtained volume of the bridge is compared with the analytically calculated volume of the cones at contact and the error is computed. The value of
$\beta _2$ is fixed from experiments or simulations to analytically calculate the volume of the double cone to be used as a parameter to verify the solution. The equation is solved and the volume of the bridge is computed numerically. The numerically obtained volume of the bridge is compared with the analytically calculated volume of the cones at contact and the error is computed. The value of ![]() $\beta _2$ obtained numerically at each iteration is compared with
$\beta _2$ obtained numerically at each iteration is compared with ![]() $\beta _2$ fixed initially and calculations are terminated if both
$\beta _2$ fixed initially and calculations are terminated if both ![]() $\beta _2$ and the volume are acceptable by varying
$\beta _2$ and the volume are acceptable by varying ![]() $r'$ and
$r'$ and ![]() $z_2$. Thus a consistent set of
$z_2$. Thus a consistent set of ![]() $\beta _1$,
$\beta _1$, ![]() $\beta _2$ and
$\beta _2$ and ![]() $z_2$ is obtained for
$z_2$ is obtained for ![]() $p=0$.
$p=0$.

Figure 13. Double cone geometry.

Figure 14. Phase diagram depicting coalescence and non-coalescence for (a) two and (b) three unequal droplets and analytically obtained phase separation boundary.
The phase boundary can be obtained by fitting the data obtained by the above procedure to an empirical equation ![]() $0.044 \beta _1+0.036\beta _2+z_2=3.467$, where
$0.044 \beta _1+0.036\beta _2+z_2=3.467$, where ![]() $\beta _1$ and
$\beta _1$ and ![]() $\beta _2$ are expressed in degrees and not radians. This plane represents the coalescence–non-coalescence criterion (henceforth called the C-NC plane). Thus one can predict coalescence or non-coalescence of droplets for a given a set of parameters
$\beta _2$ are expressed in degrees and not radians. This plane represents the coalescence–non-coalescence criterion (henceforth called the C-NC plane). Thus one can predict coalescence or non-coalescence of droplets for a given a set of parameters ![]() $\beta _1$,
$\beta _1$, ![]() $\beta _2$ and
$\beta _2$ and ![]() $z_2$ which could be obtained from boundary element calculations for a given
$z_2$ which could be obtained from boundary element calculations for a given ![]() $Ca$ and
$Ca$ and ![]() $\chi$.
$\chi$.
In the case of equal sized droplets, ![]() $\beta _1=\beta _2$ and
$\beta _1=\beta _2$ and ![]() $z_2=1$. This yields
$z_2=1$. This yields ![]() $\beta =30.8^{\circ }$, indicating congruence with the case of equal sized droplets. It will be useful to recall here that a given capillary number inscribes a specific angle
$\beta =30.8^{\circ }$, indicating congruence with the case of equal sized droplets. It will be useful to recall here that a given capillary number inscribes a specific angle ![]() $\beta$ in the case of two equal sized droplets, given by
$\beta$ in the case of two equal sized droplets, given by ![]() $\beta \sim Ca^{0.3}$, wherein it is convenient to obtain the critical
$\beta \sim Ca^{0.3}$, wherein it is convenient to obtain the critical ![]() $Ca$ by substituting
$Ca$ by substituting ![]() $\beta =30.8^{\circ }$ (Bird et al. Reference Bird, Ristenpart, Belmonte and Stone2009). This yields
$\beta =30.8^{\circ }$ (Bird et al. Reference Bird, Ristenpart, Belmonte and Stone2009). This yields ![]() $Ca_c=0.06$. In the case of two unequal sized droplets, however, the state space is increased by 2. Firstly, the two angles
$Ca_c=0.06$. In the case of two unequal sized droplets, however, the state space is increased by 2. Firstly, the two angles ![]() $\beta _1$ and
$\beta _1$ and ![]() $\beta _2$ depend on the degree of asymmetry of the two droplets, that is, the radius ratio,
$\beta _2$ depend on the degree of asymmetry of the two droplets, that is, the radius ratio, ![]() $\chi =R_2/R_1$. Moreover,
$\chi =R_2/R_1$. Moreover, ![]() $z_2$ is not necessarily equal to
$z_2$ is not necessarily equal to ![]() $z_1$, which is set as 1. This necessitates a semi-numerical approach and the numerical fitting of the plane into an empirical equation is in that spirit.
$z_1$, which is set as 1. This necessitates a semi-numerical approach and the numerical fitting of the plane into an empirical equation is in that spirit.
Figure 14(a) shows the C-NC plane, obtained from analytical theory i.e. ![]() $0.044 \beta _1+0.036\beta _2+z_2=3.467$ plotted in the coordinates
$0.044 \beta _1+0.036\beta _2+z_2=3.467$ plotted in the coordinates ![]() $\beta _1, \beta _2, z_2$ for a two droplet system. All the experimental data are also presented here for convenience. The experimental data themselves lead to realization of a plane which is best fitted by the equation,
$\beta _1, \beta _2, z_2$ for a two droplet system. All the experimental data are also presented here for convenience. The experimental data themselves lead to realization of a plane which is best fitted by the equation, ![]() $0.044\beta _1+0.036\beta _2+z_2=2.9788$. Thus, the plot shows these two planes, and the experimental data points are shown by blue and red spheres indicating coalescence and non-coalescence.
$0.044\beta _1+0.036\beta _2+z_2=2.9788$. Thus, the plot shows these two planes, and the experimental data points are shown by blue and red spheres indicating coalescence and non-coalescence.
It should be remarked here that the experimental data were obtained for both the two droplet system and the three droplet system. These experimental data are also shown in figure 14. It should be noted that, although the C-NC plane is determined only for the case of two unequal sized droplets, the analysis is valid for a three droplet system as well. This is because, in the three droplet system, the slight off-centre location of the central (inner) droplet leads to contact of the inner droplet only with one of the bigger droplets, as discussed earlier.
The figures show that the criterion of coalescence or non-coalescence as captured by the expressions derived using the analytical theory or the experiments, suffices to well represent the phenomenon. The discrepancy between analytical theory and experimental results is understandable given that, even for the system of two equal sized droplets, the critical cone angles are different, ![]() $30.8^{\circ }$ and
$30.8^{\circ }$ and ![]() $24.7^{\circ }$, respectively, due to more complex electrokinetic reasons, as discussed in Anand et al. (Reference Anand, Roy, Naik, Juvekar and Thaokar2019). However, the theory indeed captures the experimental results of coalescence and non-coalescence. The criterion for the coalescence and non-coalescence of droplets as suggested by the semi-analytical model was validated using the boundary element method. Two cases were considered, one in the coalescence regime and the other in the non-coalescence regime. The system is simulated by subjecting the three droplet system to an electric field and simulations continued until the droplets contacted. At contact, the values of
$24.7^{\circ }$, respectively, due to more complex electrokinetic reasons, as discussed in Anand et al. (Reference Anand, Roy, Naik, Juvekar and Thaokar2019). However, the theory indeed captures the experimental results of coalescence and non-coalescence. The criterion for the coalescence and non-coalescence of droplets as suggested by the semi-analytical model was validated using the boundary element method. Two cases were considered, one in the coalescence regime and the other in the non-coalescence regime. The system is simulated by subjecting the three droplet system to an electric field and simulations continued until the droplets contacted. At contact, the values of ![]() $\beta _1, \beta _2$ and
$\beta _1, \beta _2$ and ![]() $z_2$ are extracted, and the bridge is constructed as per the bridge equations. The three droplet system is then connected via the bridge and the BEM calculations are continued. Figure 15 shows that the droplets either coalesce or not depending on
$z_2$ are extracted, and the bridge is constructed as per the bridge equations. The three droplet system is then connected via the bridge and the BEM calculations are continued. Figure 15 shows that the droplets either coalesce or not depending on ![]() $Ca$ or the ratio of radius
$Ca$ or the ratio of radius ![]() $R_2/R_3$, thereby validating the model. The outcome of the contact of the droplets, coalescence or non-coalescence, obeys the equation
$R_2/R_3$, thereby validating the model. The outcome of the contact of the droplets, coalescence or non-coalescence, obeys the equation ![]() $0.044 \beta _1+0.036\beta _2+z_2=3.467$.
$0.044 \beta _1+0.036\beta _2+z_2=3.467$.

Figure 15. (a) Coalescence after bridging three droplet system obtained for ![]() $Ca = 0.15$, for
$Ca = 0.15$, for ![]() $R_2/R_3 = 0.6$, for non-dimensional times (i)
$R_2/R_3 = 0.6$, for non-dimensional times (i) ![]() $t=0$, (ii)
$t=0$, (ii) ![]() $t=0.005$, (iii)
$t=0.005$, (iii) ![]() $t = 0.01$, (iv)
$t = 0.01$, (iv) ![]() $t = 0.02$. (b) Non-coalescence after bridging three droplet system obtained for
$t = 0.02$. (b) Non-coalescence after bridging three droplet system obtained for ![]() $Ca = 0.15$, for
$Ca = 0.15$, for ![]() $R_2/R_3 = 0.2$, for non-dimensional times (i)
$R_2/R_3 = 0.2$, for non-dimensional times (i) ![]() $t = 0$, (ii)
$t = 0$, (ii) ![]() $t = 0.005$, (iii)
$t = 0.005$, (iii) ![]() $t = 0.01$, (iv)
$t = 0.01$, (iv) ![]() $t = 0.02$.
$t = 0.02$.
Thus, the semi-analytical model, if provided with ![]() $\beta _1,\beta _2$ and
$\beta _1,\beta _2$ and ![]() $z_2$, either from experiments or from simulations, can predict whether the droplets coalesce or exhibit non-coalescence. A numerical phase diagram on the
$z_2$, either from experiments or from simulations, can predict whether the droplets coalesce or exhibit non-coalescence. A numerical phase diagram on the ![]() $Ca_c-\chi$ coordinates was therefore constructed. For a given capillary number, a two or three droplet system was simulated, and the cone angles
$Ca_c-\chi$ coordinates was therefore constructed. For a given capillary number, a two or three droplet system was simulated, and the cone angles ![]() $\beta _1, \beta _2$ and
$\beta _1, \beta _2$ and ![]() $z_2$ were measured and the semi-analytical model used to deem the contact as either coalescence or non-coalescence. The phase diagram thus obtained for the two and three droplet systems is compared with the phase boundaries obtained from the experimental data (figure 16). A qualitative agreement is observed between the experiments and the simulation results. The results prove a reduction in the critical capillary number for both two unequal sized system, as well as for the three droplet system. The critical capillary number for the three droplet system is smaller than that for the two droplet system. This clearly indicates that the polydispersity and many-body interactions prevalent in an emulsion would certainly lead to a significant reduction in the critical capillary number for the onset of chaining. This is in agreement with experimental observations.
$z_2$ were measured and the semi-analytical model used to deem the contact as either coalescence or non-coalescence. The phase diagram thus obtained for the two and three droplet systems is compared with the phase boundaries obtained from the experimental data (figure 16). A qualitative agreement is observed between the experiments and the simulation results. The results prove a reduction in the critical capillary number for both two unequal sized system, as well as for the three droplet system. The critical capillary number for the three droplet system is smaller than that for the two droplet system. This clearly indicates that the polydispersity and many-body interactions prevalent in an emulsion would certainly lead to a significant reduction in the critical capillary number for the onset of chaining. This is in agreement with experimental observations.

Figure 16. Phase boundary plots as obtained from BEM and experiments for both two and three droplet systems.
5. Conclusions
Experiments and numerical simulations indicate that the critical capillary number for two unequal sized droplets is less than that for two equal sized droplets. The mechanism seems to be the greater cone angle at contact subtended by the smaller droplet on account of the strong electrohydrodynamic interaction with the bigger droplet. As expected, the critical capillary number for three equal sized droplets is smaller than that for two equal sized droplets, but, interestingly, the three unequal sized droplet system has a lower critical capillary number than the three equal sized droplet system. Our results indicate that multidroplet interaction in a polydisperse emulsion can indeed lead to a critical capillary number much smaller than that for a two equal sized droplet system. This could be one of the mechanisms for the experimental observation that the critical electric field for dehydration of a water in oil emulsion is much smaller than that predicted by the critical capillary number for a two equal sized droplet system.
Several questions remain unanswered. The discrepancy between the phase boundaries obtained experimentally and analytically remains unexplained. Similarly, the effect of finite oil and brine conductivity remains unexplored and has been shown to be important in one of our earlier studies (Anand et al. Reference Anand, Roy, Naik, Juvekar and Thaokar2019). Lastly, inertial effects ignored in this work could become important in low continuous phase viscosity systems, and would be relevant for crude oil emulsion desalters/electrocoalescers. These effects could significantly alter the static bridge assumption of Bird et al. (Reference Bird, Ristenpart, Belmonte and Stone2009), whereby the numerical predictions of the phase boundaries could improve.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2022.925.
Funding
The authors would like to acknowledge Department of Science and Technology (DST), India for financial support for this work.
Declaration of interest
The authors report no conflict of interest.