Hostname: page-component-5c6d5d7d68-thh2z Total loading time: 0 Render date: 2024-08-15T08:54:37.797Z Has data issue: false hasContentIssue false
  • English
  • Français

Elasto-inertial wall mode instabilities in viscoelastic plane Poiseuille flow

Published online by Cambridge University Press:  24 October 2019

Indresh Chaudhary Open the ORCID record for Indresh Chaudhary [Opens in a new window] ,
Piyush Garg Open the ORCID record for Piyush Garg [Opens in a new window] ,
V. Shankar Open the ORCID record for V. Shankar [Opens in a new window]  and
Ganesh Subramanian Open the ORCID record for Ganesh Subramanian [Opens in a new window]
Indresh Chaudhary
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology, Kanpur 208016, India
Piyush Garg
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore 560064, India
V. Shankar*
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology, Kanpur 208016, India
Ganesh Subramanian*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Bangalore 560064, India
*
†Email addresses for correspondence: vshankar@iitk.ac.in, sganesh@jncasr.ac.in
†Email addresses for correspondence: vshankar@iitk.ac.in, sganesh@jncasr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

A linear stability analysis of plane Poiseuille flow of an upper-convected Maxwell (UCM) fluid, bounded between rigid plates separated by a distance 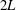$2L$, has been carried out to investigate the interplay of elasticity and inertia on flow stability. The stability is governed by the following dimensionless groups: the Reynolds number 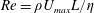$Re=\unicode[STIX]{x1D70C}U_{max}L/\unicode[STIX]{x1D702}$ and the elasticity number 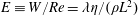$E\equiv W/Re=\unicode[STIX]{x1D706}\unicode[STIX]{x1D702}/(\unicode[STIX]{x1D70C}L^{2})$, where 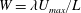$W=\unicode[STIX]{x1D706}U_{max}/L$ is the Weissenberg number. Here, 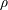$\unicode[STIX]{x1D70C}$ is the fluid density, 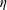$\unicode[STIX]{x1D702}$ is the fluid viscosity, 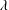$\unicode[STIX]{x1D706}$ is the micro-structural relaxation time and 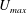$U_{max}$ is the maximum base-flow velocity. The stability is analysed for two-dimensional perturbations using both pseudo-spectral and shooting methods. We also analyse the linear stability of plane Couette flow which, along with the results for plane Poiseuille flow, yields insight into the structure of the complete elasto-inertial eigenspectrum. While the general features of the spectrum for both flows remain similar, plane Couette flow is found to be stable over the range of parameters examined (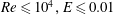$Re\leqslant 10^{4},E\leqslant 0.01$). On the other hand, plane Poiseuille flow appears to be susceptible to an infinite hierarchy of elasto-inertial instabilities. Over the range of parameters examined, there are up to seven distinct neutral stability curves in the 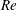$Re$–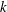$k$ plane (here 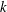$k$ is the perturbation wavenumber in the flow direction). Based on the symmetry of the eigenfunctions for the streamwise velocity about the centreline, four of these instabilities are antisymmetric, while the other three are symmetric. The neutral stability curve corresponding to the first antisymmetric mode is shown to be a continuation (to finite 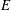$E$) of the Tollmien–Schlichting (TS) instability already present for Newtonian channel flow. As 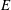$E$ is increased beyond 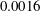$0.0016$, a new elastic mode appears at 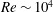$Re\sim 10^{4}$, which coalesces with the continuation of the TS mode for a range of 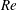$Re$, thereby yielding a single unstable mode in this range. This trend persists until 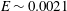$E\sim 0.0021$, beyond which this neutral curve splits into two separate ones in the 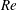$Re$–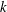$k$ plane. The new elastic mode which arises out of this splitting has been found to be the most unstable, with the lowest critical Reynolds number 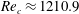$Re_{c}\approx 1210.9$ for 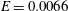$E=0.0066$. The neutral curves for both the continuation of the original TS mode, and the new elastic antisymmetric mode, form closed loops upon further increase in 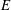$E$, which eventually vanish at sufficiently high 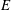$E$. For 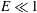$E\ll 1$, the critical Reynolds number and wavenumber scale as 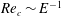$Re_{c}\sim E^{-1}$ and 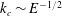$k_{c}\sim E^{-1/2}$ for the first two of the symmetric modal families, and as 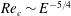$Re_{c}\sim E^{-5/4}$ for first two of the antisymmetric modal families; 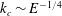$k_{c}\sim E^{-1/4}$ for the third antisymmetric family. The critical wave speed for all of these unstable eigenmodes scales as 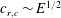$c_{r,c}\sim E^{1/2}$ for 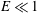$E\ll 1$, implying that the modes belong to a class of ‘wall modes’ in viscoelastic flows with disturbances being confined in a thin region near the wall. The present study shows that, surprisingly, even in plane shear flows, elasticity acting along with inertia can drive novel instabilities absent in the Newtonian limit.

JFM classification

Non-Newtonian Flows: Viscoelasticity
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 881 , 25 December 2019 , pp. 119 - 163
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, K., Moxey, D., Lozar, A. D., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333, 192–196.Google Scholar
Bender, C. M. & Orszag, S. A. 2013 Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory. Springer Science & Business Media.Google Scholar
Bertola, V., Meulenbroek, B., Wagner, C., Storm, C., Morozov, A., van Saarloos, W. & Bonn, D. 2003 Experimental evidence for an intrinsic route to polymer melt fracture phenomena: a nonlinear instability of viscoelastic Poiseuille flow. Phys. Rev. Lett. 90, 114502.Google Scholar
Bistagnino, A., Boffetta, G., Celani, A., Mazzino, A., Puliafito, A. & Vergassola, M. 2007 Nonlinear dynamics of the viscoelastic Kolmogorov flow. J. Fluid Mech. 590, 61–80.Google Scholar
Budanur, N. B., Short, K. Y., Farazmand, M., Willis, A. P. & Cvitanović, P. 2017 Relative periodic orbits form the backbone of turbulent pipe flow. J. Fluid Mech. 833, 274–301.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1988 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Carlson, D. R., Windall, S. E. & Peters, M. F. 1982 A flow-visualization study of transition in plane Poiseuille flow. J. Fluid Mech. 121, 487–505.Google Scholar
Castillo, H. A. & Wilson, H. J. 2017 Towards a mechanism for instability in channel flow of highly shear-thinning viscoelastic fluids. J. Non-Newtonian Fluid Mech. 247, 15–21.Google Scholar
Chandra, B., Shankar, V. & Das, D. 2018 Onset of transition in the flow of polymer solutions through microtubes. J. Fluid Mech. 844, 1052–1083.Google Scholar
Chokshi, P. & Kumaran, V. 2009 Stability of the plane shear flow of dilute polymeric solutions. Phys. Fluids 21, 014109.Google Scholar
Choueiri, G. H., Lopez, J. M. & Hof, B. 2018 Exceeding the asymptotic limit of polymer drag reduction. Phys. Rev. Lett. 120, 124501.Google Scholar
Cromer, M., Fredrickson, G. H. & Leal, L. G. 2014 A study of shear banding in polymer solutions. Phys. Fluids 26, 063101.Google Scholar
Cromer, M., Villet, M. C., Fredrickson, G. H. & Leal, L. G. 2013 Shear banding in polymer solutions. Phys. Fluids 25, 051703.Google Scholar
Doering, C. R., Eckhardt, B. & Schumacher, J. 2006 Failure of energy stability in Oldroyd-b fluids at arbitrarily low Reynolds numbers. J. Non-Newtonian Fluid Mech. 135 (2), 92–96.Google Scholar
Drazin, P. G. 2002 Introduction to Hydrodynamic Stability. Cambridge University Press.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability, 2nd edn. Cambridge University Press.Google Scholar
Dubief, Y., Terrapon, V. E. & Soria, J. 2013 On the mechanism of elasto-inertial turbulence. Phys. Fluids 25, 110817.Google Scholar
Dubief, Y., Terrapon, V. E., White, C. M., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2005 New answers on the interaction between polymers and vortices in turbulent flows. Flow Turbul. Combust. 74, 311–329.Google Scholar
Dubief, Y., White, C. M., Terrapon, V. E., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2004 On the coherent drag-reducing and turbulence-enhancing behaviour of polymers in wall flows. J. Fluid Mech. 514, 271–280.Google Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.Google Scholar
Garg, P., Chaudhary, I., Khalid, M., Shankar, V. & Subramanian, G. 2018 Viscoelastic pipe flow is linearly unstable. Phys. Rev. Lett. 121, 024502.Google Scholar
Gorodtsov, V. A. & Leonov, A. I. 1967 On a linear instability of a plane parallel Couette flow of viscoelastic fluid. Z. Angew. Math. Mech. J. Appl. Math. Mech. 31, 310–319.Google Scholar
Graham, M. D. 1998 Effect of axial flow on viscoelastic Taylor–Couette instability. J. Fluid Mech. 360, 341–374.Google Scholar
Graham, M. D. 2014 Drag reduction and the dynamics of turbulence in simple and complex fluids. Phys. Fluids 26, 625–656.Google Scholar
Grillet, A. M., Bogaerds, A. C. B., Peters, G. W. M. & Baaijens, F. P. T. 2002 Stability analysis of constitutive equations for polymer melts in viscometric flows. J. Non-Newtonian Fluid Mech. 103, 221–250.Google Scholar
Ho, T. C. & Denn, M. M. 1977 Stability of plane Poiseuille flow of a highly elastic liquid. J. Non-Newtonian Fluid Mech. 3, 179–195.Google Scholar
Hoda, N., Jovanovic, M. R. & Kumar, S. 2008 Energy amplification in channel flows of viscoelastic fluids. J. Fluid Mech. 601, 407–424.Google Scholar
Hoda, N., Jovanovic, M. R. & Kumar, S. 2009 Frequency responses of streamwise-constant perturbations in channel flows of Oldroyd-B fluids. J. Fluid Mech. 625, 411–434.Google Scholar
Hof, B., de Lozar, A., Avila, M., Tu, X. & Schneider, T. M. 2010 Eliminating turbulence in spatially intermittent flows. Science 327, 1491–1494.Google Scholar
Hof, B., de Lozar, A., Kuik, D. J. & Westerweel, J. 2008 Repeller or attractor? Selecting the dynamical model for the onset of turbulence in pipe flow. Phys. Rev. Lett. 101, 214501.Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Joo, Y. L. & Shaqfeh, E. S. G. 1992 The effects of inertia on the viscoelastic Dean and Taylor–Couette flow instabilities with application to coating flows. Phys. Fluids A 4, 2415–2431.Google Scholar
Jovanovic, M. R. & Kumar, S. 2010 Transient growth without inertia. Phys. Fluids 22, 023101.Google Scholar
Jovanovic, M. R. & Kumar, S. 2011 Nonmodal amplification of stochastic disturbances in strongly elastic channel flows. J. Non-Newtonian Fluid Mech. 166, 755–778.Google Scholar
Kumar, A. S. & Shankar, V. 2005 Instability of high-frequency modes in viscoelastic plane Couette flow past a deformable wall at low and finite Reynolds number. J. Non-Newtonian Fluid Mech. 125, 121–141.Google Scholar
Larson, R. G. 1988 Constitutive Equations for Polymer Melts and Solutions. Butterworths.Google Scholar
Lee, K. C. & Finlayson, B. A. 1986 Stability of plane Poiseuille and Couette flow of a Maxwell fluid. J. Non-Newtonian Fluid Mech. 21, 65–78.Google Scholar
Lin, C. C. 1945 On the stability of two-dimensional parallel flows. I. General theory. Q. Appl. Maths 3, 117–142.Google Scholar
Liu, R. & Liu, Q. 2010 Non-modal instabilities of two-dimensional disturbances in plane Couette flow of a power-law fluid. J. Non-Newtonian Fluid Mech. 165, 1228–1240.Google Scholar
Mack, L. M. 1976 A numerical study of the temporal eigenvalue spectrum of the Blasius boundary layer. J. Fluid Mech. 73, 497–520.Google Scholar
Metzner, A. B. & Park, M. G. 1964 Turbulent flow characteristics of viscoelastic fluids. J. Fluid Mech. 20, 291–303.Google Scholar
Meulenbroek, B., Storm, C., Bertola, V., Wagner, C., Bonn, D. & van Saarloos, W. 2003 Intrinsic route to melt fracture in polymer extrusion: a weakly nonlinear subcritical instability of viscoelastic Poiseuille flow. Phys. Rev. Lett. 90, 024502.Google Scholar
Meulenbroek, B., Storm, C., Morozov, A. N. & van Saarloos, W. 2004 Weakly nonlinear subcritical instability of viscoelastic Poiseuille flow. J. Non-Newtonian Fluid Mech. 116, 235–268.Google Scholar
Morozov, A. N. & van Saarloos, W. 2005 Subcritical finite-amplitude solutions for plane Couette flow of viscoelastic fluids. Phys. Rev. Lett. 95, 024501.Google Scholar
Morozov, A. N. & van Saarloos, W. 2007 An introductory essay on subcritical instabilities and the transition to turbulence in viscoelastic parallel shear flows. Phys. Rep. 447, 112–143.Google Scholar
Muller, S. J. 2008 Elastically-influenced instabilities in Taylor–Couette and other flows with curved streamlines: a review. Korea-Australi Rheology J. 20, 117–125.Google Scholar
Mullin, T. 2011 Experimental studies of transition to turbulence in a pipe. Annu. Rev. Fluid Mech. 43, 1–24.Google Scholar
Nishioka, M. & Asai, M. 1985 Some observations of the subcritical transition in plane Poiseuille flow. J. Fluid Mech. 150, 441–450.Google Scholar
Orszag, S. A. & Kells, L. C. 1980 Transition to turbulence in plane Poiseuille and plane Couette flow. J. Fluid Mech. 96, 159–205.Google Scholar
Page, J. & Zaki, T. A. 2014 Streak evolution in viscoelastic Couette flow. J. Fluid Mech. 742, 520–551.Google Scholar
Pan, L., Morozov, A., Wagner, C. & Arratia, P. E. 2013 Nonlinear elastic instability in channel flows at low Reynolds numbers. Phys. Rev. Lett. 110, 174502.Google Scholar
Patel, V. C. & Head, M. R. 1969 Some observations on skin friction and velocity profiles in fully developed pipe and channel flows. J. Fluid Mech. 38, 181–201.Google Scholar
Poole, R. J. 2012 The Deborah and Weissenberg numbers. Rheol. Bull. 53, 32–39.Google Scholar
Poole, R. J. 2016 Elastic instabilities in parallel shear flows of a viscoelastic shear-thinning liquid. Phys. Rev. Fluids 1, 041301.Google Scholar
Porteous, K. C. & Denn, M. M. 1972 Linear stability of plane Poiseuille flow of viscoelastic liquids. Trans. Soc. Rheol. 16, 295–308.Google Scholar
Renardy, M. 1992 A rigorous stability proof for plane Couette flow of an upper convected Maxwell fluid at zero Reynolds number. Eur. J. Mech. (B/Fluids) 11 (4), 511–516.Google Scholar
Renardy, M. & Renardy, Y. 1986 Linear stability of plane Couette flow of an upper convected Maxwell fluid. J. Non-Newtonian Fluid Mech. 22, 23–33.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Roy, A., Morozov, A., van Saarloos, W. & Larson, R. G. 2006 Mechanism of polymer drag reduction using a low-dimensional model. Phys. Rev. Lett. 97, 234501.Google Scholar
Sadanandan, B. & Sureshkumar, R. 2002 Viscoelastic effects on the stability of wall-bounded shear flows. Phys. Fluids 14, 41–48.Google Scholar
Samanta, D., Dubief, Y., Holzner, M., Schäfer, C., Morozov, A. N., Wagner, C. & Hof, B. 2013 Elasto-inertial turbulence. Proc. Natl Acad. Sci. USA 110, 10557–10562.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Seyer, F. A. & Metzner, A. B. 1969 Turbulence phenomena in drag reducing systems. AIChE J. 15, 426–434.Google Scholar
Shaqfeh, E. S. G. 1996 Purely elastic instabilities in viscometric flows. Annu. Rev. Fluid Mech. 28, 129–185.Google Scholar
Shekar, A., McMullen, R. M., Wang, S. N., McKeon, B. J. & Graham, M. D. 2019 Critical-layer structures and mechanisms in elastoinertial turbulence. Phys. Rev. Lett. 122, 124503.Google Scholar
Sid, S., Terrapon, V. E. & Dubief, Y. 2018 Two-dimensional dynamics of elasto-inertial turbulence and its role in polymer drag reduction. Phys. Rev. Fluids 3, 011301(R).Google Scholar
Srinivas, S. S. & Kumaran, V. 2017 Effect of viscoelasticity on the soft-wall transition and turbulence in a microchannel. J. Fluid Mech. 812, 1076–1118.Google Scholar
Stone, P. A. & Graham, M. D. 2003 Polymer dynamics in a model of the turbulent buffer layer. Phys. Fluids 15, 1247–1256.Google Scholar
Stone, P. A., Roy, A., Larson, R. G., Waleffe, F. & Graham, M. D. 2004 Polymer drag reduction in exact coherent structures of plane shear flow. Phys. Fluids 16, 3470–3482.Google Scholar
Stone, P. A., Waleffe, F. & Graham, M. D. 2002 Toward a structural understanding of turbulent drag reduction: nonlinear coherent states in viscoelastic shear flows. Phys. Rev. Lett. 89, 208301.Google Scholar
Sureshkumar, R. 2000 Numerical observations on the continuous spectrum of the linearized viscoelastic operator in shear dominated complex flows. J. Non-Newtonian Fluid Mech. 94, 205–211.Google Scholar
Sureshkumar, R. & Beris, A. N. 1995a Effect of artificial stress diffusivity on the stability of numerical calculations and the flow dynamics of time-dependent viscoelastic flows. J. Non-Newtonian Fluid Mech. 60, 53–80.Google Scholar
Sureshkumar, R. & Beris, A. N. 1995b Linear stability analysis of viscoelastic Poiseuille flow using an Arnoldi-based orthogonalization algorithm. J. Non-Newtonian Fluid Mech. 56, 151–182.Google Scholar
Sureshkumar, R., Beris, A. N. & Handler, R. A. 1997 Direct numerical simulation of the turbulent channel flow of a polymer solution. Phys. Fluids 9, 743–755.Google Scholar
Virk, P. S. 1975 Drag reduction fundamentals. AIChE J. 21, 625–656.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Wen, C., Poole, R. J., Willis, A. P. & Dennis, D. J. C. 2017 Experimental evidence of symmetry-breaking supercritical transition in pipe flow of shear-thinning fluids. Phys. Rev. Fluids 2, 031901.Google Scholar
White, C. M. & Mungal, M. G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40, 235–256.Google Scholar
Wilson, H. J. & Loridan, V. 2015 Linear instability of a highly shear-thinning fluid in channel flow. J. Non-Newtonian Fluid Mech. 223, 200–208.Google Scholar
Wilson, H. J. & Rallison, J. M. 1999 Instability of channel flow of a shear-thinning whitemetzner fluid. J. Non-Newtonian Fluid Mech. 87, 75–96.Google Scholar
Wilson, H. J., Renardy, M. & Renardy, Y. 1999 Structure of the spectrum in zero Reynolds number shear flow of the UCM and Oldroyd-B liquids. J. Non-Newtonian Fluid Mech. 80, 251–268.Google Scholar
Zhang, M., Lashgari, I., Zaki, T. A. & Brandt, L. 2013 Linear stability analysis of channel flow of viscoelastic Oldroyd-B and FENE-P fluids. J. Fluid Mech. 737, 249–279.Google Scholar