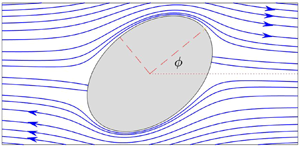
It is shown that shape anisotropy and intrinsic surface slip lead to equilibrium tilt of slippery particles in a creeping simple shear flow, even for nearly shape-isotropic particles with a cross-section that is close to circular provided the Navier-slip length is sufficiently large. We study a rigid particle with an elliptical cross-section, and of infinite extent in the vorticity direction, in simple shear. A Navier-slip boundary condition is imposed on its surface. When a Navier-slip length parameter $\lambda$ is infinite, an analytical solution is derived for the Stokes flow around a particle tilting in equilibrium at an angle $(1/2)\cos ^{-1}((1-k)/(1+k))$ to the flow direction where $0 \le k \le 1$ is the ratio of the semi-minor to semi-major axes of its elliptical cross-section. A regular perturbation analysis about this analytical solution is then performed for small values of $1/\lambda$ and a numerical continuation method implemented for larger values. It is found that an equilibrium continues to exist for any anisotropic particle $k < 1$ provided $\lambda \ge \lambda _{crit}(k)$ where $\lambda _{crit}(k)$ is a critical Navier-slip length parameter determined here. As the case $k \to 1$ of a circular cross-section is approached, it is found that $\lambda _{crit}(k) \to \infty$, so the range of Navier-slip lengths allowing equilibrium tilt shrinks as shape anistropy is lost. Novel theoretical connections with equilibria for constant-pressure gas bubbles with surface tension are also pointed out.