Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-06-08T03:46:53.697Z Has data issue: false hasContentIssue false
  • English
  • Français

Experimental investigation of flow-induced vibration and flow field characteristics of a flexible triangular cylinder

Published online by Cambridge University Press:  10 January 2024

Seyedmohammad Mousavisani Open the ORCID record for Seyedmohammad Mousavisani [Opens in a new window] ,
Hamed Samandari Open the ORCID record for Hamed Samandari [Opens in a new window]  and
Banafsheh Seyed-Aghazadeh Open the ORCID record for Banafsheh Seyed-Aghazadeh [Opens in a new window]
Seyedmohammad Mousavisani
Affiliation:
Department of Mechanical Engineering, University of Massachusetts, Dartmouth, MA 02747, USA
Hamed Samandari
Affiliation:
Department of Mechanical Engineering, University of Massachusetts, Dartmouth, MA 02747, USA
Banafsheh Seyed-Aghazadeh*
Affiliation:
Department of Mechanical Engineering, University of Massachusetts, Dartmouth, MA 02747, USA
*
†Email address for correspondence: b.aghazadeh@umassd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

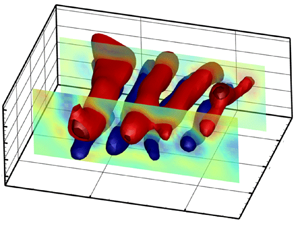
Flow-induced vibration (FIV) of a flexible cylinder with a triangular cross-section, allowed to oscillate in the cross-flow, inline and torsional direction, is studied experimentally through water tunnel tests. The dynamic response of the cylinder was studied for three different angles of attack ($0^\circ, 30^\circ, 60^\circ$), at reduced velocities of 0.9–16.27, corresponding to Reynolds numbers of 364–3600. At the angle of attack of $0^\circ$, vortex-induced vibration at low reduced velocity was observed, which transitioned to galloping at higher reduced velocities. At the angles of attack of $30^\circ$ and $60^\circ$, galloping-type response was observed over the range of the reduced velocities tested. Our results show that the cylinder's torsional oscillation breaks the system's symmetry and affects the structural response at higher reduced velocities regardless of the angle of attack. The FIV response of the flexible triangular cylinder is distinct from that of a rigid flexibly mounted triangular cylinder due to torsional oscillation, spanwise flexibility and the two fixed boundary conditions limiting the amplitude of oscillation. Flow field analysis in the wake of the cylinder was done qualitatively and quantitatively using hydrogen bubble flow visualisation and time-resolved volumetric particle tracking velocimetry techniques, respectively. Our results show the existence of highly three-dimensional vortex structures in the wake of the cylinder. We studied the coupling between the vortex shedding modes in the wake of the cylinder and the structural vibration modes through the spatiotemporal mode analysis using the proper orthogonal decomposition technique to distinguish between different types of the FIV response observed.

JFM classification

Vortex Flows: Vortex dynamics Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 979 , 25 January 2024 , A15
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alonso, G. & Meseguer, J. 2006 A parametric study of the galloping stability of two-dimensional triangular cross-section bodies. J. Wind Engng Ind. Aerodyn. 94 (4), 241–253.CrossRefGoogle Scholar
Alonso, G., Meseguer, J. & Pérez-Grande, I. 2005 Galloping instabilities of two-dimensional triangular cross-section bodies. Exp. Fluids 38 (6), 789–795.CrossRefGoogle Scholar
Alonso, G., Meseguer, J. & Pérez-Grande, I. 2007 Galloping stability of triangular cross-sectional bodies: a systematic approach. J. Wind Engng Ind. Aerodyn. 95 (9), 928–940.CrossRefGoogle Scholar
Alonso, G., Sanz-Lobera, A. & Meseguer, J. 2012 Hysteresis phenomena in transverse galloping of triangular cross-section bodies. J. Fluids Struct. 33, 243–251.CrossRefGoogle Scholar
Bao, Y., Zhou, D. & Zhao, Y.-J. 2010 A two-step Taylor-characteristic-based Galerkin method for incompressible flows and its application to flow over triangular cylinder with different incidence angles. Intl J. Numer. Meth. Fluids 62 (11), 1181–1208.CrossRefGoogle Scholar
Bearman, P.W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J.L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.CrossRefGoogle Scholar
Bourguet, R., Karniadakis, G.E. & Triantafyllou, M.S. 2011 a Vortex-induced vibrations of a long flexible cylinder in shear flow. J. Fluid Mech. 677, 342–382.CrossRefGoogle Scholar
Bourguet, R., Karniadakis, G.E. & Triantafyllou, M.S. 2013 Distributed lock-in drives broadband vortex-induced vibrations of a long flexible cylinder in shear flow. J. Fluid Mech. 717, 361–375.CrossRefGoogle Scholar
Bourguet, R., Lucor, D. & Triantafyllou, M.S. 2012 Mono-and multi-frequency vortex-induced vibrations of a long tensioned beam in shear flow. J. Fluids Struct. 32, 52–64.CrossRefGoogle Scholar
Bourguet, R., Modarres-Sadeghi, Y., Karniadakis, G.E. & Triantafyllou, M.S. 2011 b Wake-body resonance of long flexible structures is dominated by counterclockwise orbits. Phys. Rev. Lett. 107 (13), 134502.CrossRefGoogle ScholarPubMed
Cen, H. 2015 Flow-induced vibration of a flexible circular cylinder. Master's thesis, University of Windsor, Ontario, Canada.CrossRefGoogle Scholar
Chanthanasaro, T. 2020 Sound and wake characteristics generated by flow past a triangular cylinder at various incident angles. PhD thesis, Mahidol University.CrossRefGoogle Scholar
Chanthanasaro, T. & Boonyasiriwat, C. 2021 Numerical study on characteristics of sound and wake generated by flow past triangular cylinder at various incident angles. 1719 (1), 012034.Google Scholar
Chaplin, J.R., Bearman, P.W., Huarte, F.J.H. & Pattenden, R.J. 2005 Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current. J. Fluids Struct. 21 (1), 3–24.CrossRefGoogle Scholar
Chen, L., Wu, J. & Cheng, B. 2019 Volumetric measurement and vorticity dynamics of leading-edge vortex formation on a revolving wing. Exp. Fluids 60 (1), 1–15.CrossRefGoogle Scholar
Chen, W., Ji, C., Alam, Md.M., Xu, D., An, H., Tong, F. & Zhao, Y. 2022 Flow-induced vibrations of a D-section prism at a low Reynolds number. J. Fluid Mech. 941, A52.CrossRefGoogle Scholar
Chen, W., Ji, C., Xu, D., Zhang, Z. & Wei, Y. 2020 Flow-induced vibrations of an equilateral triangular prism at various angles of attack. J. Fluids Struct. 97, 103099.CrossRefGoogle Scholar
Dahl, J.M., Hover, F.S. & Triantafyllou, M.S. 2006 Two-degree-of-freedom vortex-induced vibrations using a force assisted apparatus. J. Fluids Struct. 22 (6–7), 807–818.CrossRefGoogle Scholar
Dahl, J.M., Hover, F.S., Triantafyllou, M.S., Dong, S. & Karniadakis, G.Em. 2007 Resonant vibrations of bluff bodies cause multivortex shedding and high frequency forces. Phys. Rev. Lett. 99 (14), 144503.CrossRefGoogle ScholarPubMed
Deep, D., Sahasranaman, A. & Senthilkumar, S. 2022 Pod analysis of the wake behind a circular cylinder with splitter plate. Eur. J. Mech. (B/Fluids) 93, 1–12.CrossRefGoogle Scholar
Evangelinos, C. & Karniadakis, G.Em. 1999 Dynamics and flow structures in the turbulent wake of rigid and flexible cylinders subject to vortex-induced vibrations. J. Fluid Mech. 400, 91–124.CrossRefGoogle Scholar
Evangelinos, C., Lucor, D. & Karniadakis, G.E. 2000 DNS-derived force distribution on flexible cylinders subject to vortex-induced vibration. J. Fluids Struct. 14 (3), 429–440.CrossRefGoogle Scholar
Fan, D., Wang, Z., Triantafyllou, M.S. & Karniadakis, G.Em. 2019 Mapping the properties of the vortex-induced vibrations of flexible cylinders in uniform oncoming flow. J. Fluid Mech. 881, 815–858.CrossRefGoogle Scholar
Govardhan, R. & Williamson, C.H.K. 2002 Resonance forever: existence of a critical mass and an infinite regime of resonance in vortex-induced vibration. J. Fluid Mech. 473, 147–166.CrossRefGoogle Scholar
Holmes, P., Lumley, J.L., Berkooz, G. & Rowley, C.W. 2012 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.CrossRefGoogle Scholar
Huera-Huarte, F.J. & Bearman, P.W. 2009 Wake structures and vortex-induced vibrations of a long flexible cylinder—part 1: dynamic response. J. Fluids Struct. 25 (6), 969–990.CrossRefGoogle Scholar
Jauvtis, N. & Williamson, C.H.K. 2004 The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 509, 23.CrossRefGoogle Scholar
Khalak, A & Williamson, C.H.K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7), 813–851.CrossRefGoogle Scholar
Kumar De, A. & Dalal, A. 2006 Numerical simulation of unconfined flow past a triangular cylinder. Intl J. Numer. Meth. Fluids 52 (7), 801–821.CrossRefGoogle Scholar
Kumar De, A. & Dalal, A. 2007 Numerical study of laminar forced convection fluid flow and heat transfer from a triangular cylinder placed in a channel.CrossRefGoogle Scholar
Lie, H. & Kaasen, K.E. 2006 Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow. J. Fluids Struct. 22 (4), 557–575.CrossRefGoogle Scholar
Liu, X., Gui, N., Wu, H., Yang, X., Tu, J. & Jiang, S. 2020 Numerical simulation of flow past a triangular prism with fluid–structure interaction. Engng Appl. Comput. Fluid Mech. 14 (1), 462–476.Google Scholar
Marcollo, H., Eassom, A., Fontaine, E., Tognarelli, M., Beynet, P., Constantinides, Y. & Oakley, O.H. Jr. 2011 Traveling wave response in full-scale drilling riser VIV measurements. In International Conference on Offshore Mechanics and Arctic Engineering, vol. 44397, pp. 523–537.Google Scholar
Massai, T., Zhao, J., Jacono, D.L., Bartoli, G. & Sheridan, J. 2018 The effect of angle of attack on flow-induced vibration of low-side-ratio rectangular cylinders. J. Fluids Struct. 82, 375–393.CrossRefGoogle Scholar
Menon, K. & Mittal, R. 2021 On the initiation and sustenance of flow-induced vibration of cylinders: insights from force partitioning. J. Fluid Mech. 907, A37.CrossRefGoogle Scholar
Modir, A., Ahani, H., Mohammadkhani, A. & Mousavisani, M. 2021 The fluid-induced vibration of cylinders with non-circular cross-sections in a water channel. J. Ocean Engng 7 (3), 277–286.Google Scholar
Mousavisani, S., Castro, G. & Seyed-Aghazadeh, B. 2022 a Experimental investigation on flow-induced vibration of two high mass-ratio flexible cylinders in tandem arrangement. J. Fluids Struct. 113, 103640.CrossRefGoogle Scholar
Mousavisani, S., Chowdhury, N.N., Samsam-Khayani, H., Samandari, H. & Seyed-Aghazadeh, B. 2022 b Vortex-induced vibration of a two degree-of-freedom flexibly mounted circular cylinder in the crossflow direction. J. Fluid Mech. 952, A26.CrossRefGoogle Scholar
Nemes, A., Zhao, J., Lo Jacono, D. & Sheridan, J. 2012 The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack. J. Fluid Mech. 710, 102–130.CrossRefGoogle Scholar
Ng, Z.Y., Vo, T., Hussam, W.K. & Sheard, G.J. 2016 Two-dimensional wake dynamics behind cylinders with triangular cross-section under incidence angle variation. J. Fluids Struct. 63, 302–324.CrossRefGoogle Scholar
Ng, Z.Y., Vo, T. & Sheard, G.J. 2018 Stability of the wakes of cylinders with triangular cross-sections. J. Fluid Mech. 844, 721–745.CrossRefGoogle Scholar
Obasaju, E.D., Ermshaus, R. & Naudascher, E. 1990 Vortex-induced streamwise oscillations of a square-section cylinder in a uniform stream. J. Fluid Mech. 213, 171–189.CrossRefGoogle Scholar
Paidoussis, M.P. (Ed.) 2014 Fluid-Structure Interactions, 2nd edn. Academic.Google Scholar
Raghavan, K. & Bernitsas, M.M. 2011 Experimental investigation of Reynolds number effect on vortex induced vibration of rigid circular cylinder on elastic supports. Ocean Engng 38 (5), 719–731.CrossRefGoogle Scholar
Riches, G., Martinuzzi, R. & Morton, C. 2018 Proper orthogonal decomposition analysis of a circular cylinder undergoing vortex-induced vibrations. Phys. Fluids 30 (10), 105103.CrossRefGoogle Scholar
Sarpkaya, T. 1995 Hydrodynamic damping, flow-induced oscillations, and biharmonic response. Trans. ASME J. Offshore Mech. Arctic Engng 117 (4).Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.CrossRefGoogle Scholar
Schanz, D., Gesemann, S. & Schröder, A. 2016 Shake-the-box: Lagrangian particle tracking at high particle image densities. Exp. Fluids 57 (5), 1–27.CrossRefGoogle Scholar
Seyed-Aghazadeh, B., Anderson, N. & Dulac, S. 2021 a Flow-induced vibration of high-mass ratio isolated and tandem flexible cylinders with fixed boundary conditions. J. Fluids Struct. 103, 103276.CrossRefGoogle Scholar
Seyed-Aghazadeh, B., Benner, B., Gjokollari, X. & Modarres-Sadeghi, Y. 2021 b An experimental investigation of vortex-induced vibration of a curved flexible cylinder. J. Fluid Mech. 927.CrossRefGoogle Scholar
Seyed-Aghazadeh, B., Carlson, D.W. & Modarres-Sadeghi, Y. 2017 Vortex-induced vibration and galloping of prisms with triangular cross-sections. J. Fluid Mech. 817, 590–618.CrossRefGoogle Scholar
Seyed-Aghazadeh, B., Edraki, M. & Modarres-Sadeghi, Y. 2019 Effects of boundary conditions on vortex-induced vibration of a fully submerged flexible cylinder. Exp. Fluids 60 (3), 1–14.CrossRefGoogle Scholar
Seyed-Aghazadeh, B. & Modarres-Sadeghi, Y. 2016 Reconstructing the vortex-induced-vibration response of flexible cylinders using limited localized measurement points. J. Fluids Struct. 65, 433–446.CrossRefGoogle Scholar
Seyed-Aghazadeh, B. & Modarres-Sadeghi, Y. 2018 An experimental study to investigate the validity of the independence principle for vortex-induced vibration of a flexible cylinder over a range of angles of inclination. J. Fluids Struct. 78, 343–355.CrossRefGoogle Scholar
Sharma, G., Garg, H. & Bhardwaj, R. 2022 Flow-induced vibrations of elastically-mounted C- and D-section cylinders. J. Fluids Struct. 109, 103501.CrossRefGoogle Scholar
Taira, K., Brunton, S.L., Dawson, S.T.M., Rowley, C.W., Colonius, T., McKeon, B.J., Schmidt, O.T., Gordeyev, S., Theofilis, V. & Ukeiley, L.S. 2017 Modal analysis of fluid flows: an overview. AIAA J. 55 (12), 4013–4041.CrossRefGoogle Scholar
Tamimi, V., Naeeni, S.T.O., Zeinoddini, M., Seif, M.S. & Pirooz, M.D. 2019 Effects of after-body on the fiv of a right-angle triangular cylinder in comparison to circular, square, and diamond cross-sections. Ships Offshore Struct. 14 (6), 589–599.CrossRefGoogle Scholar
Trim, A.D., Braaten, H., Lie, H. & Tognarelli, M.A. 2005 Experimental investigation of vortex-induced vibration of long marine risers. J. Fluids Struct. 21 (3), 335–361.CrossRefGoogle Scholar
Tu, J., Zhou, D., Bao, Y., Han, Z. & Li, R. 2014 Flow characteristics and flow-induced forces of a stationary and rotating triangular cylinder with different incidence angles at low Reynolds numbers. J. Fluids Struct. 45, 107–123.CrossRefGoogle Scholar
Vandiver, J.K., Marcollo, H., Swithenbank, S., Jhingran, V. 2005 High mode number vortex-induced vibration field experiments. In Offshore Technology Conference, pp. OTC–17383. OTC.CrossRefGoogle Scholar
Weiss, J. 2019 A tutorial on the proper orthogonal decomposition. In AIAA aviation 2019 forum, p. 3333.Google Scholar
Zanganeh, H. & Srinil, N. 2016 Three-dimensional VIV prediction model for a long flexible cylinder with axial dynamics and mean drag magnifications. J. Fluids Struct. 66, 127–146.CrossRefGoogle Scholar
Zhao, J., Hourigan, K. & Thompson, M.C. 2018 Flow-induced vibration of D-section cylinders: an afterbody is not essential for vortex-induced vibration. J. Fluid Mech. 851, 317–343.CrossRefGoogle Scholar
Zhu, H., Ping, H., Wang, R., Bao, Y., Zhou, D., Wei, X. & Han, Z. 2020 Dynamic response of a cable with triangular cross section subject to uniform flow at Reynolds number 3900. Phys. Fluids 32 (4), 045103.CrossRefGoogle Scholar
Zhu, H.B., Ping, H., Wang, R., Bao, Y., Zhou, D. & Han, Z.L. 2019 Flow-induced vibration of a flexible triangular cable at low Reynolds numbers. Phys. Fluids 31 (5), 057101.CrossRefGoogle Scholar
Supplementary material: File

Mousavisani et al. supplementary movie 1

Hydrogen bubble flow visualization of the wake at the mid-span of the cylinder at the reduced velocity of U*=4.73 and angle of attack of α = 0◦
Download Mousavisani et al. supplementary movie 1(File)
File 39.6 MB
Supplementary material: File

Mousavisani et al. supplementary movie 2

Hydrogen bubble flow visualization of the wake at the mid-span of the cylinder at the reduced velocity of U*=6.38 and angle of attack of α = 30◦
Download Mousavisani et al. supplementary movie 2(File)
File 39.9 MB
Supplementary material: File

Mousavisani et al. supplementary movie 3

Hydrogen bubble flow visualization of the wake at the mid-span of the cylinder at the reduced velocity of U*=4.73 and angle of attack of α = 60◦
Download Mousavisani et al. supplementary movie 3(File)
File 39.9 MB