Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-06-06T10:40:49.064Z Has data issue: false hasContentIssue false
  • English
  • Français

Extended Darcy–Forchheimer law including inertial flow deflection effects

Published online by Cambridge University Press:  31 January 2024

Mostafa Aghaei-Jouybari Open the ORCID record for Mostafa Aghaei-Jouybari [Opens in a new window] ,
Jung-Hee Seo Open the ORCID record for Jung-Hee Seo [Opens in a new window] ,
Sasindu Pinto Open the ORCID record for Sasindu Pinto [Opens in a new window] ,
Louis Cattafesta Open the ORCID record for Louis Cattafesta [Opens in a new window] ,
Charles Meneveau Open the ORCID record for Charles Meneveau [Opens in a new window]  and
Rajat Mittal Open the ORCID record for Rajat Mittal [Opens in a new window]
Mostafa Aghaei-Jouybari
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Jung-Hee Seo
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Sasindu Pinto
Affiliation:
Department of Mechanical, Materials, and Aerospace Engineering, Illinois Institute of Technology, Chicago, IL 60616, USA
Louis Cattafesta
Affiliation:
Department of Mechanical, Materials, and Aerospace Engineering, Illinois Institute of Technology, Chicago, IL 60616, USA
Charles Meneveau
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Rajat Mittal*
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: mittal@jhu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

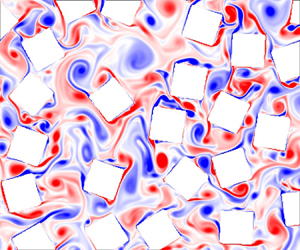
Recent advances in manufacturing techniques are providing porous media with both high permeability, necessary for effective passive flow control, and high structural strength, essential for engineering applications. We therefore examine the predictive accuracy of the standard Darcy–Forchheimer (DF) law, which is often used to model porous media flows, for inclusion Reynolds numbers (Re) ranging from the low linear regime to the high nonlinear regime where unsteady effects such as vortex shedding become evident. We consider two different inclusion shapes, square and circular, and three different arrangements of the inclusions – inline, staggered and random. The numerical simulations show that the DF law performs well for low-Re flows, irrespective of the inclusion configuration. For intermediate/high-Re flows, the DF law is adequate only when the arrangement is highly random. However, for the regularly arranged topologies or less random geometries at intermediate/high-Re flows, the DF-law performance diminishes significantly due to flow sheltering and redirection (‘inertial flow deflection’) effects that arise from flow inertia, separation and vortex shedding in the wake of the inclusions. It is shown that the standard DF law, in which the nonlinear permeability tensor is independent of orientation, does not capture such effects. We modified the DF law to capture flow redirection effects by allowing the Forchheimer permeability tensor to depend on the flow orientation with respect to the principal geometrical directions of the porous geometry, and examined this extended DF law for these flows.

JFM classification

Low-Reynolds-number flows: Porous media Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 980 , 10 February 2024 , A13
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abidoye, L.K., Khudaida, K.J. & Das, D.B. 2015 Geological carbon sequestration in the context of two-phase flow in porous media: a review. Crit. Rev. Environ. Sci. Technol. 45 (11), 1105–1147.CrossRefGoogle Scholar
Aghaei-Jouybari, M., Seo, J.H., Yuan, J., Mittal, R. & Meneveau, C. 2022 Contributions to pressure drag in rough-wall turbulent flows: insights from force partitioning. Phys. Rev. Fluids 7, 084602.CrossRefGoogle Scholar
Agnaou, M., Lasseux, D. & Ahmadi, A. 2016 From steady to unsteady laminar flow in model porous structures: an investigation of the first hopf bifurcation. Comput. Fluids 136, 67–82.CrossRefGoogle Scholar
Agnaou, M., Lasseux, D. & Ahmadi, A. 2017 Origin of the inertial deviation from darcy's law: an investigation from a microscopic flow analysis on two-dimensional model structures. Phys. Rev. E 96, 043105.CrossRefGoogle Scholar
Brinkman, H.C. 1949 A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Flow Turbul. Combust. 1 (1), 27–34.CrossRefGoogle Scholar
Bruneau, C.H., Lasseux, D. & Valdés-Parada, F.J. 2020 Comparison between direct numerical simulations and effective models for fluid-porous flows using penalization. Meccanica 55 (5), 1061–1077.CrossRefGoogle Scholar
Carman, P.C. 1937 Fluid flow through a granular bed. Trans. Inst. Chem. Engng 15, 150–156.Google Scholar
Chavarin, A., Gómez-de Segura, G., García-Mayoral, R. & Luhar, M. 2021 Resolvent-based predictions for turbulent flow over anisotropic permeable substrates. J. Fluid Mech. 913, A24.CrossRefGoogle Scholar
Chen, Z., Lyons, S.L. & Qin, G. 2001 Derivation of the forchheimer law via homogenization. Transp. Porous Media 44 (2), 325–335.CrossRefGoogle Scholar
Defraeye, T., Blocken, B., Derome, D., Nicolai, B. & Carmeliet, J. 2012 Convective heat and mass transfer modelling at air–porous material interfaces: overview of existing methods and relevance. Chem. Engng Sci. 74, 49–58.CrossRefGoogle Scholar
Edwards, D.A., Shapiro, M., Bar-Yoseph, P. & Shapira, M. 1990 The influence of Reynolds number upon the apparent permeability of spatially periodic arrays of cylinders. Phys. Fluids A 2 (1), 45–55.CrossRefGoogle Scholar
Forchheimer, P.H. 1901 Wasserbewegung durch Boden. Z. Verein. Deutsch. Ing. 45.Google Scholar
Gómez-de Segura, G. & García-Mayoral, R. 2019 Turbulent drag reduction by anisotropic permeable substrates – analysis and direct numerical simulations. J. Fluid Mech. 875, 124–172.CrossRefGoogle Scholar
Guest, J.K. & Szyniszewski, S. 2021 Three dimensional woven lattices for drag reduction and turbulence reduction (US Patent No. 11168718).Google Scholar
Higdon, J.J.L. 2013 Multiphase flow in porous media. J. Fluid Mech. 730, 1–4.CrossRefGoogle Scholar
Ho, C.K. & Webb, S.W. 2006 Gas Transport in Porous Media, vol. 20. Springer.CrossRefGoogle Scholar
Jansen, J.D. 2011 Adjoint-based optimization of multi-phase flow through porous media – a review. Comput. Fluids 46 (1), 40–51.CrossRefGoogle Scholar
Joseph, D.D., Nield, D.A. & Papanicolaou, G. 1982 Nonlinear equation governing flow in a saturated porous medium. Water Resour. Res. 18 (4), 1049–1052.CrossRefGoogle Scholar
Knupp, P.M. & Lage, J.L. 1995 Generalization of the forchheimer-extended darcy flow model to the tensor premeability case via a variational principle. J. Fluid Mech. 299, 97–104.CrossRefGoogle Scholar
Kozeny, J. 1927 Über kapillare leitung des wassers im boden. Sitzungsberichte der Akademie der Wissenschaften in Wien. 136, 271.Google Scholar
Kutscher, K., Geier, M. & Krafczyk, M. 2019 Multiscale simulation of turbulent flow interacting with porous media based on a massively parallel implementation of the cumulant lattice Boltzmann method. Comput. Fluids 193, 103733.CrossRefGoogle Scholar
Kuwata, Y. & Suga, K. 2016 Lattice boltzmann direct numerical simulation of interface turbulence over porous and rough walls. Intl J. Heat Fluid Flow 61, 145–157.CrossRefGoogle Scholar
Kuwata, Y., Tsuda, K. & Suga, K. 2020 Direct numerical simulation of turbulent conjugate heat transfer in a porous-walled duct flow. J. Fluid Mech. 904, A9.CrossRefGoogle Scholar
Lasseux, D., Abbasian Arani, A.A. & Ahmadi, A. 2011 On the stationary macroscopic inertial effects for one phase flow in ordered and disordered porous media. Phys. Fluids 23 (7), 073103.CrossRefGoogle Scholar
Medici, G., Smeraglia, L., Torabi, A. & Botter, C. 2021 Review of modeling approaches to groundwater flow in deformed carbonate aquifers. Groundwater 59 (3), 334–351.CrossRefGoogle ScholarPubMed
Mei, C.C. & Auriault, J.-L. 1991 The effect of weak inertia on flow through a porous medium. J. Fluid Mech. 222, 647–663.CrossRefGoogle Scholar
Mittal, R. & Balachandar, S. 1995 Effect of three-dimensionality on the lift and drag of nominally two-dimensional cylinders. Phys. Fluids 7 (8), 1841–1865.CrossRefGoogle Scholar
Mittal, R., Dong, H., Bozkurttas, M., Najjar, F.M., Vargas, A. & Von Loebbecke, A. 2008 A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 227 (10), 4825–4852.CrossRefGoogle ScholarPubMed
Pelacci, M., Robins, A.G. & Szyniszewski, S. 2021 Drag reduction of a circular cylinder through the use of an architectured lattice material. arXiv:2102.08938.Google Scholar
Pillai, M.A. & Deenadayalan, E. 2014 A review of acoustic energy harvesting. Intl J. Precis. Engng Manuf. 15 (5), 949–965.CrossRefGoogle Scholar
Rao, F., Kuznetsov, A.V. & Jin, Y. 2020 Numerical modeling of momentum dispersion in porous media based on the pore scale prevalence hypothesis. Transp. Porous Media 133 (2), 271–292.CrossRefGoogle Scholar
Rosti, M.E., Brandt, L. & Pinelli, A. 2018 Turbulent channel flow over an anisotropic porous wall – drag increase and reduction. J. Fluid Mech. 842, 381–394.CrossRefGoogle Scholar
Samanta, A., Vinuesa, R., Lashgari, I., Schlatter, P. & Brandt, L. 2015 Enhanced secondary motion of the turbulent flow through a porous square duct. J. Fluid Mech. 784, 681–693.CrossRefGoogle Scholar
Seo, J.H. & Mittal, R. 2011 A sharp-interface immersed boundary method with improved mass conservation and reduced spurious pressure oscillations. J. Comput. Phys. 230 (19), 7347–7363.CrossRefGoogle ScholarPubMed
Shen, G., Yuan, J. & Phanikumar, M.S. 2020 Direct numerical simulations of turbulence and hyporheic mixing near sediment–water interfaces. J. Fluid Mech. 892, A20.CrossRefGoogle Scholar
Suga, K., Okazaki, Y. & Kuwata, Y. 2020 Characteristics of turbulent square duct flows over porous media. J. Fluid Mech. 884, A7.CrossRefGoogle Scholar
Wang, X., Thauvin, F. & Mohanty, K.K. 1999 Non-darcy flow through anisotropic porous media. Chem. Engng Sci. 54 (12), 1859–1869.CrossRefGoogle Scholar
Wang, Y., Ahmadi, A. & Lasseux, D. 2019 On the inertial single phase flow in 2d model porous media: role of microscopic structural disorder. Transp. Porous Media 128 (1), 201–220.CrossRefGoogle Scholar
Ward, J.C. 1964 Turbulent flow in porous media. J. Hydraul. Div. 90 (5), 1–12.CrossRefGoogle Scholar
Whitaker, S. 1996 The Forchheimer equation: a theoretical development. Transp. Porous Media 25 (1), 27–61.CrossRefGoogle Scholar
Wood, B.D., He, X. & Apte, S.V. 2020 Modeling turbulent flows in porous media. Annu. Rev. Fluid Mech. 52 (1), 171–203.CrossRefGoogle Scholar