Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T09:05:20.063Z Has data issue: false hasContentIssue false
  • English
  • Français

Heated transcritical and unheated non-transcritical turbulent boundary layers at supercritical pressures

Published online by Cambridge University Press:  20 February 2019

Soshi Kawai Open the ORCID record for Soshi Kawai [Opens in a new window]
Soshi Kawai*
Affiliation:
Department of Aerospace Engineering, Tohoku University, Sendai, Miyagi 980-8579, Japan
*
†Email address for correspondence: kawai@cfd.mech.tohoku.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Nominally zero-pressure-gradient fully developed flat-plate turbulent boundary layers with heated and unheated isothermal walls at supercritical pressures are studied by solving the full compressible Navier–Stokes equations using direct numerical simulation. With a heated isothermal wall, the wall temperature sets such that the flow temperature varies through the pseudo-critical temperature, and thus pseudo-boiling phenomena occur within the boundary layers. The pseudo-boiling process induces strongly nonlinear real-fluid effects in the flow and interacts with near-wall turbulence. The peculiar abrupt density variations through the pseudo-boiling process induce significant near-wall density fluctuations 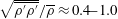$\sqrt{\overline{\unicode[STIX]{x1D70C}^{\prime }\unicode[STIX]{x1D70C}^{\prime }}}/\overline{\unicode[STIX]{x1D70C}}\approx 0.4{-}1.0$ within the heated transcritical turbulent boundary layers. The large near-wall density fluctuations induce a turbulent mass flux 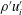$\unicode[STIX]{x1D70C}^{\prime }u_{i}^{\prime }$, and the turbulent mass flux amplifies the Favre-averaged velocity fluctuations 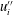$u_{i}^{\prime \prime }$ in the near-wall predominant structures of streamwise low-speed streaks that are associated with the ejection (where 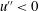$u^{\prime \prime }<0$ and 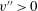$v^{\prime \prime }>0$), while reducing the velocity fluctuations in the high-speed streaks associated with the sweep (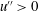$u^{\prime \prime }>0$ and 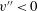$v^{\prime \prime }<0$). Although the near-wall low-speed and high-speed streak structures dominate the Reynolds-shear-stress generation, the energized Favre-averaged velocity fluctuations in the low-speed streaks enhance both the mean-density- and density-fluctuation-related Reynolds shear stresses (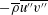$-\overline{\unicode[STIX]{x1D70C}}\overline{u^{\prime \prime }v^{\prime \prime }}$ and 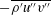$-\overline{\unicode[STIX]{x1D70C}^{\prime }u^{\prime \prime }v^{\prime \prime }}$) in the ejection event and, as a result, alter the Reynolds-shear-stress profile. The large density fluctuations also alter the near-wall viscous-stress profile and induce a near-wall convective flux 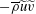$-\overline{\unicode[STIX]{x1D70C}}\widetilde{u}\widetilde{v}$ (due to non-zero 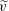$\widetilde{v}$). The changes in the contributions in the stress-balance equation result in a failure of existing velocity transformations to collapse to the universal law of the wall. The large density fluctuations also greatly contribute to the turbulent kinetic energy budget, and especially the mass flux contribution term becomes noticeable as one of the main positive terms. The unheated non-transcritical turbulent boundary layers show a negligible contribution of the real-fluid effects, and the turbulence statistics agree well with the statistics of an incompressible constant-property turbulent boundary layer with a perfect-gas law.

JFM classification

Compressible Flows: Compressible boundary layers Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 865 , 25 April 2019 , pp. 563 - 601
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abgrall, R. 1996 How to prevent pressure oscillations in multicomponent flow calculations: a quasi conservative approach. J. Comput. Phys. 125 (1), 150–160.10.1006/jcph.1996.0085Google Scholar
Abgrall, R. & Karni, S. 2001 Computations of compressible multifluids. J. Comput. Phys. 169 (2), 594–623.10.1006/jcph.2000.6685Google Scholar
Bae, J. H., Yoo, J. Y. & Choi, H. 2005 Direct numerical simulation of turbulent supercritical flows with heat transfer. Phys. Fluids 17 (10), 105104.10.1063/1.2047588Google Scholar
Bae, J. H., Yoo, J. Y. & Mceligot, D. M. 2008 Direct numerical simulation of heated CO2 flows at supercritical pressure in a vertical annulus at re = 8900. Phys. Fluids 20 (5), 055108.10.1063/1.2927488Google Scholar
Bellmore, C. P. & Reid, R. L. 1983 Numerical prediction of wall temperatures for near-critical para-hydrogen in turbulent upflow inside vertical tubes. Trans. ASME J. Heat Transfer 105 (3), 536–541.10.1115/1.3245618Google Scholar
Cheng, X., Kuang, B. & Yang, Y. H. 2007 Numerical analysis of heat transfer in supercritical water cooled flow channels. Nucl. Engng Des. 237 (3), 240–252.10.1016/j.nucengdes.2006.06.011Google Scholar
Chung, T.-H., Ajlan, M., Lee, L. L. & Starling, K. E. 1988 Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Engng Chem. Res. 27 (4), 671–679.10.1021/ie00076a024Google Scholar
Ely, J. F. & Hanley, H. J. M. 1981 Prediction of transport properties. 1. Viscosity of fluids and mixtures. Ind. Engng Chem. Res. 20 (4), 323–332.Google Scholar
Foysi, H., Sarkar, S. & Friedrich, R. 2004 Compressibility effects and turbulence scalings in supersonic channel flow. J. Fluid Mech. 509, 207–216.10.1017/S0022112004009371Google Scholar
Gaitonde, D. V. & Visbal, M. R. 2000 Padé-type higher-order boundary filters for the Navier–Stokes equations. AIAA J. 38 (11), 2103–2112.10.2514/2.872Google Scholar
He, S., Kim, W. S. & Bae, J. H. 2008 Assessment of performance of turbulence models in predicting supercritical pressure heat transfer in a vertical tube. Intl J. Heat Mass Transfer 51 (19–20), 4659–4675.10.1016/j.ijheatmasstransfer.2007.12.028Google Scholar
Hickey, J.-P., Ma, P. C., Ihme, M. & Thakur, S.2013 Large eddy simulation of shear coaxial rocket injector: real fluid effects. AIAA Paper 2013–4071. AIAA.Google Scholar
Huang, P. G., Coleman, G. N. & Bradshaw, P. 1995 Compressible turbulent channel flows: DNS results and modelling. J. Fluid Mech. 305, 185–218.10.1017/S0022112095004599Google Scholar
Johnsen, E. & Colonius, T. 2006 Implementation of WENO schemes in compressible multicomponent flow problems. J. Comput. Phys. 219 (2), 715–732.10.1016/j.jcp.2006.04.018Google Scholar
Karni, S. 1996 Hybrid multifluid algorithms. SIAM J. Sci. Comput. 17 (5), 1019–1039.10.1137/S106482759528003XGoogle Scholar
Kawai, S. & Fujii, K. 2008 Compact scheme with filtering for large-eddy simulation of transitional boundary layer. AIAA J. 46 (3), 690–700.10.2514/1.32239Google Scholar
Kawai, S. & Lele, S. K. 2010 Large-eddy simulation of jet mixing in supersonic crossflows. AIAA J. 48 (9), 2063–2083.10.2514/1.J050282Google Scholar
Kawai, S., Terashima, H. & Negishi, H. 2015 A robust and accurate numerical method for transcritical turbulent flows at supercritical pressure with an arbitrary equation of state. J. Comput. Phys. 300, 116–135.10.1016/j.jcp.2015.07.047Google Scholar
Kim, H. T., Kline, S. J. & Reynolds, W. C. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50, 133–160.10.1017/S0022112071002490Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.10.1017/S0022112067001740Google Scholar
Lee, J., Jung, S. Y., Sung, H. J. & Zaki, T. A. 2013 Effect of wall heating on turbulent boundary layers with temperature-dependent viscosity. J. Fluid Mech. 726, 196–225.10.1017/jfm.2013.211Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.10.1016/0021-9991(92)90324-RGoogle Scholar
Masi, E., Bellan, J., Harstad, K. G. & Okong’o, N. A. 2013 Multi-species turbulent mixing under supercritical-pressure conditions: modelling, direct numerical simulation and analysis revealing species spinodal decomposition. J. Fluid Mech. 721, 578–626.10.1017/jfm.2013.70Google Scholar
Miller, R. S. & Bellan, J. 1999 Direct numerical simulation of a confined three-dimensional gas mixing layer with one evaporating hydrocarbon-droplet-laden stream. J. Fluid Mech. 384, 293–338.10.1017/S0022112098004042Google Scholar
Miller, R. S., Harstad, K. G. & Bellan, J. 2001 Direct numerical simulations of supercritical fluid mixing layers applied to heptane-nitrogen. J. Fluid Mech. 436, 1–39.10.1017/S0022112001003895Google Scholar
Nemati, H., Patel, A., Boersma, B. J. & Pecnik, R. 2015 Mean statistics of a heated turbulent pipe flow at supercritical pressure. Intl J. Heat Mass Transfer 83, 741–752.10.1016/j.ijheatmasstransfer.2014.12.039Google Scholar
Nemati, H., Patel, A., Boersma, B. J. & Pecnik, R. 2016 The effect of thermal boundary conditions on forced convection heat transfer to fluids at supercritical pressure. J. Fluid Mech. 800, 531–556.10.1017/jfm.2016.411Google Scholar
Okong’o, N. A. & Bellan, J. 2002 Direct numerical simulation of a transitional supercritical binary mixing layer: heptane and nitrogen. J. Fluid Mech. 464, 1–34.Google Scholar
Patel, A., Boersma, B. J. & Pecnik, R. 2016 The influence of near-wall density and viscosity gradients on turbulence in channel flows. J. Fluid Mech. 809, 793–820.10.1017/jfm.2016.689Google Scholar
Patel, A., Peeters, J. W. R., Boersma, B. J. & Pecnik, R. 2015 Semi-local scaling and turbulence modulation in variable property turbulent channel flows. Phys. Fluids 27 (9), 095101.10.1063/1.4929813Google Scholar
Peeters, J. W. R., Pecnik, R., van der Hagen, J. H. J. J. & Boersma, B. J. 2016 Turbulent attenuation in simultaneously heated and cooled annular flows at supercritical pressure. J. Fluid Mech. 799, 505–540.10.1017/jfm.2016.383Google Scholar
Peng, D. Y. & Robinson, D. B. 1976 A new two-constant equation of state. Ind. Engng Chem. Res. 15 (1), 59–64.Google Scholar
Pirozzoli, S., Grasso, F. & Gatski, T. B. 2004 Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer at M = 2. 25. Phys. Fluids 16 (3), 530–545.10.1063/1.1637604Google Scholar
Shu, C. W. & Osher, S. J. 1988 Efficient implementation of essentially nonoscillatory shock capturing schemes. J. Comput. Phys. 77 (2), 439–471.10.1016/0021-9991(88)90177-5Google Scholar
Shyue, K. M. 1998 An efficient shock-capturing algorithm for compressible multicomponent problems. J. Comput. Phys. 142 (1), 208–242.10.1006/jcph.1998.5930Google Scholar
Soave, G. 1972 Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Engng Sci. 27 (6), 1197–1203.10.1016/0009-2509(72)80096-4Google Scholar
Spalart, R. P. 1988 Direct simulation of a turbulent boundary layer up to r 𝜃 = 1410. J. Fluid Mech. 187, 61–98.10.1017/S0022112088000345Google Scholar
Terashima, H. & Koshi, M. 2012 Approach for simulating gas-liquid-like flows under supercritical pressures using a high-order central differencing scheme. J. Comput. Phys. 231 (20), 6907–6923.10.1016/j.jcp.2012.06.021Google Scholar
Trettel, A. & Larsson, J. 2016 Mean velocity scaling for compressible wall turbulence with heat transfer. Phys. Fluids 28 (2), 026102.10.1063/1.4942022Google Scholar
Urbin, G. & Knight, D. 2001 Large-eddy simulation of a supersonic boundary layer using an unstructured grid. AIAA J. 39 (7), 1288–1295.10.2514/2.1471Google Scholar
Van Driest, E. R. 1951 Turbulent boundary layer in compressible fluids. J. Aeronaut. Sci. 18 (3), 145–160.10.2514/8.1895Google Scholar
Wallace, J. M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 48, 131–158.10.1146/annurev-fluid-122414-034550Google Scholar
Yamagata, K., Nishikawa, K., Hasegawa, S., Fujii, T. & Yoshida, S. 1972 Forced convective heat transfer to supercritical water flowing in tubes. Intl J. Heat Mass Transfer 15 (12), 2575–2593.10.1016/0017-9310(72)90148-2Google Scholar
Yang, J., Oka, Y., Ishiwatari, Y., Liu, J. & Yoo, J. 2007 Numerical investigation of heat transfer in upward flows of supercritical water in circular tubes and tight fuel rod bundles. Nucl. Engng Des. 237 (3), 420–430.10.1016/j.nucengdes.2006.08.003Google Scholar
Yoo, J. Y. 2013 The turbulent flows of supercritical fluids with heat transfer. Annu. Rev. Fluid Mech. 45, 495–525.10.1146/annurev-fluid-120710-101234Google Scholar
Zonta, F., Marchioli, C. & Soldati, A. 2012 Modulation of turbulence in forced convection by temperature-dependent viscosity. J. Fluid Mech. 697, 150–174.10.1017/jfm.2012.67Google Scholar