Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-18T13:50:01.813Z Has data issue: false hasContentIssue false
  • English
  • Français

Impact of pressure dissipation on fluid injection into layered aquifers

Published online by Cambridge University Press:  19 August 2019

Luke T. Jenkins Open the ORCID record for Luke T. Jenkins [Opens in a new window] ,
Martino Foschi Open the ORCID record for Martino Foschi [Opens in a new window]  and
Christopher W. MacMinn Open the ORCID record for Christopher W. MacMinn [Opens in a new window]
Luke T. Jenkins
Affiliation:
Department of Earth Sciences, University of Oxford, OxfordOX1 3AN, UK Department of Engineering Science, University of Oxford, OxfordOX1 3PJ, UK
Martino Foschi
Affiliation:
Department of Earth Sciences, University of Oxford, OxfordOX1 3AN, UK
Christopher W. MacMinn*
Affiliation:
Department of Engineering Science, University of Oxford, OxfordOX1 3PJ, UK
*
†Email address for correspondence: christopher.macminn@eng.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Carbon dioxide (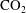$\text{CO}_{2}$) capture and subsurface storage is one method for reducing anthropogenic 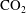$\text{CO}_{2}$ emissions to mitigate climate change. It is well known that large-scale fluid injection into the subsurface leads to a buildup in pressure that gradually spreads and dissipates through lateral and vertical migration of water. This dissipation can have an important feedback on the shape of the $\text{CO}_{2}$ plume during injection, but the impact of vertical pressure dissipation, in particular, remains poorly understood. Here, we investigate the impact of lateral and vertical pressure dissipation on the injection of 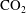$\text{CO}_{2}$ into a layered aquifer system. We develop a compressible, two-phase model that couples pressure dissipation to the propagation of a 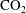$\text{CO}_{2}$ gravity current. We show that our vertically integrated, sharp-interface model is capable of efficiently and accurately capturing water migration in a layered aquifer system with an arbitrary number of aquifers. We identify two limiting cases – ‘no leakage’ and ‘strong leakage’ – in which we derive analytical expressions for the water pressure field for the corresponding single-phase injection problem. We demonstrate that pressure dissipation acts to suppress the formation of an advancing 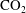$\text{CO}_{2}$ tongue during injection, reducing the lateral extent of the plume. The properties of the seals and the number of aquifers determine the strength of pressure dissipation and subsequent coupling with the 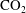$\text{CO}_{2}$ plume. The impact of pressure dissipation on the shape of the 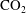$\text{CO}_{2}$ plume is likely to be important for storage efficiency and security.

JFM classification

Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 877 , 25 October 2019 , pp. 214 - 238
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barenblatt, G. I. 1996 Scaling, Self-similarity, and Intermediate Asymptotics. Cambridge University Press.10.1017/CBO9781107050242Google Scholar
Bear, J. 1972 Dynamics of Fluids in Porous Media. Courier Corporation.Google Scholar
Bear, J. 1979 Hydraulics of Groundwater. Courier Corporation.Google Scholar
Birkholzer, J. T., Zhou, Q. & Tsang, C.-F. 2009 Large-scale impact of CO2 storage in deep saline aquifers: a sensitivity study on pressure response in stratified systems. Intl J. Greenh. Gas Control 3 (2), 181–194.10.1016/j.ijggc.2008.08.002Google Scholar
Chang, K. W., Hesse, M. A. & Nicot, J. P. 2013 Reduction of lateral pressure propagation due to dissipation into ambient mudrocks during geological carbon dioxide storage. Water Resour. Res. 49 (5), 2573–2588.10.1002/wrcr.20197Google Scholar
Gasda, S. E., Nordbotten, J. M. & Celia, M. A. 2009 Vertical equilibrium with sub-scale analytical methods for geological CO2 sequestration. Comput. Geosci. 79 (1), 15–27.Google Scholar
Golding, M. J., Huppert, H. E. & Neufeld, J. A. 2017 Two-phase gravity currents resulting from the release of a fixed volume of fluid in a porous medium. J. Fluid Mech. 832, 550–577.10.1017/jfm.2017.437Google Scholar
Golding, M. J., Neufeld, J. A., Hesse, M. A. & Huppert, H. E. 2011 Two-phase gravity currents in porous media. J. Fluid Mech. 678, 248–270.10.1017/jfm.2011.110Google Scholar
Green, D. H. & Wang, H. F. 1990 Specific storage as a poroelastic coefficient. Water Resour. Res. 26 (7), 1631–1637.10.1029/WR026i007p01631Google Scholar
Hesse, M. A., Orr, F. M. Jr. & Tchelepi, H. A. 2008 Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60.10.1017/S002211200800219XGoogle Scholar
Hesse, M. A., Tchelepi, H. A., Cantwell, B. J. & Orr, F. M. Jr. 2007 Gravity currents in horizontal porous layers: transition from early to late self-similarity. J. Fluid Mech. 577, 363–383.10.1017/S0022112007004685Google Scholar
Hewitt, D. R., Neufeld, J. A. & Balmforth, N. J. 2015 Shallow, gravity-driven flow in a poro-elastic layer. J. Fluid Mech. 778, 335–360.10.1017/jfm.2015.361Google Scholar
Hunt, B. 1985 Flow to a well in a multiaquifer system. Water Resour. Res. 21 (11), 1637–1641.10.1029/WR021i011p01637Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.10.1017/S0022112095001431Google Scholar
IPCC 2005 Carbon Dioxide Capture and Storage. Special Report prepared by Working Group III of the Intergovernmental Panel on Climate Change.Google Scholar
Juanes, R., MacMinn, C. W. & Szulczewski, M. L. 2010 The footprint of the CO2 plume during carbon dioxide storage in saline aquifers: storage efficiency for capillary trapping at the basin scale. Trans. Porous Med. 82 (1), 19–30.Google Scholar
Kochina, I. N., Mikhailov, N. N. & Filinov, M. V. 1983 Groundwater mound damping. Intl J. Engng Sci. 21 (4), 413–421.Google Scholar
de Loubens, R. & Ramakrishnan, T. S. 2011 Analysis and computation of gravity-induced migration in porous media. J. Fluid Mech. 675, 60–86.10.1017/S0022112010006440Google Scholar
MacMinn, C. W. & Juanes, R. 2009 Post-injection spreading and trapping of CO2 in saline aquifers: impact of the plume shape at the end of injection. Comput. Geosci. 13 (4), 483–491.10.1007/s10596-009-9147-9Google Scholar
MacMinn, C. W., Szulczewski, M. L. & Juanes, R. 2010 CO2 migration in saline aquifers. Part 1. Capillary trapping under slope and groundwater flow. J. Fluid Mech. 662, 329–351.10.1017/S0022112010003319Google Scholar
MacMinn, C. W., Szulczewski, M. L. & Juanes, R. 2011 CO2 migration in saline aquifers. Part 2. Capillary and solubility trapping. J. Fluid Mech. 688, 321–351.10.1017/jfm.2011.379Google Scholar
Mathias, S. A., González Martínez de Miguel, G. J., Thatcher, K. E. & Zimmerman, R. W. 2011 Pressure buildup during CO2 injection into a closed brine aquifer. Trans. Porous Med. 89 (3), 383–397.Google Scholar
Mathias, S. A., Hardisty, P. E., Trudell, M. R. & Zimmerman, R. W. 2009 Approximate solutions for pressure buildup during CO2 injection in brine aquifers. Trans. Porous Med. 79 (2), 265–284.Google Scholar
Nicot, J.-P. 2008 Evaluation of large-scale CO2 storage on fresh-water sections of aquifers: an example from the Texas Gulf Coast Basin. Intl J. Greenh. Gas Control 2 (4), 582–593.10.1016/j.ijggc.2008.03.004Google Scholar
Nicot, J.-P., Hosseini, S. A. & Solano, S. V. 2011 Are single-phase flow numerical models sufficient to estimate pressure distribution in CO2 sequestration projects? In Energy Procedia (Proceedings of the 10th International Conference on Greenhouse Gas Control Technologies), vol. 4, pp. 3919–3926. Elsevier.Google Scholar
Nordbotten, J. M. & Celia, M. A. 2006a An improved analytical solution for interface upconing around a well. Water Resour. Res. 42 (8), W08433.Google Scholar
Nordbotten, J. M. & Celia, M. A. 2006b Similarity solutions for fluid injection into confined aquifers. J. Fluid Mech. 561, 307–327.10.1017/S0022112006000802Google Scholar
Nordbotten, J. M., Celia, M. A. & Bachu, S. 2005 Injection and storage of CO2 in deep saline aquifers: analytical solution for CO2 plume evolution during injection. Trans. Porous Med. 58 (3), 339–360.Google Scholar
Pegler, S. S., Huppert, H. E. & Neufeld, J. A. 2014 Fluid injection into a confined porous layer. J. Fluid Mech. 745, 592–620.10.1017/jfm.2014.76Google Scholar
Shampine, L. F. & Reichelt, M. W. 1997 The MATLAB ODE suite. SIAM J. Sci. Comput. 18 (1), 1–22.10.1137/S1064827594276424Google Scholar
Szulczewski, M. L., MacMinn, C. W., Herzog, H. J. & Juanes, R. 2012 Lifetime of carbon capture and storage as a climate-change mitigation technology. Proc. Natl Acad. Sci. USA 109 (14), 5185–5189.10.1073/pnas.1115347109Google Scholar
Teige, G. M. G., Thomas, W. L. H., Hermanrud, C., Øren, P.-E., Rennan, L., Wilson, O. B. & Nordgård Bolås, H. G. 2006 Relative permeability to wetting-phase water in oil reservoirs. J. Geophys. Res. 111, B12204.10.1029/2005JB003804Google Scholar
van der Kamp, G. & Gale, J. E. 1983 Theory of Earth tide and barometric effects in porous formations with compressible grains. Water Resour. Res. 19 (2), 538–544.10.1029/WR019i002p00538Google Scholar
Vilarrasa, V., Bolster, D., Dentz, M., Olivella, S. & Carrera, J. 2010 Effects of CO2 compressibility on CO2 storage in deep saline aquifers. Trans. Porous Med. 85 (2), 619–639.Google Scholar
Yortsos, Y. C. 1995 A theoretical analysis of vertical flow equilibrium. Trans. Porous Med. 18 (2), 107–129.Google Scholar
Zheng, Z., Guo, B., Christov, I. C., Celia, M. A. & Stone, H. A. 2015 Flow regimes for fluid injection into a confined porous medium. J. Fluid Mech. 767, 881–909.10.1017/jfm.2015.68Google Scholar