3.3.1. Convergence of a CMS with initial uniform intensity

The convergence of a CMS is selected as a typical case to validate the FDTM, which can be equivalent to the axisymmetric ICS generated by a ring wedge (i.e. $AR = 1.0$) in the present study. On the one hand, this typical case is a baseline that can be compared with the EMSs in § 4. On the other hand, much theoretical and experimental research on the convergence of the CMS has been performed (Guderley Reference Guderley1942; Takayama et al. Reference Takayama, Kleine and Grönig1987; Hornung, Pullin & Ponchaut Reference Hornung, Pullin and Ponchaut2008); thus, the accuracy of the FDTM can be validated by the theoretical evolution of the cylindrical shock front (Hornung et al. Reference Hornung, Pullin and Ponchaut2008) and the theoretical characteristics in GSD (Han & Yin Reference Han and Yin1993). The initial radius of the CMS is $R_0=a$, and the initial moving shock Mach number is $M_{{s0}}=1.9$, which is equivalent to the axisymmetric ICS generated by a ring wedge with $\delta _0=10^{\circ }$ in $M_\infty =6$.

The initial shock front is discretized circumferentially with an equal length in the FDTM. Three sets of initial lengths with ${\rm \Delta} s_0/S_0=5\times 10^{-3}$, ${\rm \Delta} s_0/S_0=2.5\times 10^{-3}$ and ${\rm \Delta} s_0/S_0=1.25\times 10^{-3}$ are tested, corresponding to the initial discrete point numbers of 200, 400 and 800, where ${\rm \Delta} s_0$ and $S_0$ are the length of the shock segment in the ray tube and the circumference of the cylindrical shock itself at initial time $t=0$, respectively. Although the CMS can converge to the centre, the convergence of the axisymmetric ICS is terminated early by the Mach disk before the converging centre (Zhang et al. Reference Zhang, Li, Ji, Si and Yang2021). To keep the equivalence between the CMS and the axisymmetric ICS, the convergence termination of the CMS in the FDTM is set as $t/T=2.62$ with $T=a/V_\infty$, which corresponds to the position of the Mach disk at $x/a=2.62$ in the axisymmetric ICS (Zhang et al. Reference Zhang, Li, Ji, Si and Yang2021; Ji et al. Reference Ji, Li, Zhang, Si and Yang2022).

As shown in figure 6(a), the variations in the shock front radius ($R$) with time $t$ calculated by the FDTM with three sets of discrete points are compared with the theoretical solution reported by Hornung et al. (Reference Hornung, Pullin and Ponchaut2008) who used the integral form of the relation (3.1) to obtain the theoretical evolution of the CMS. The horizontal and vertical coordinates in figure 6(a) maintain the scale of $1:1$ to illustrate the real shape of the shock front. To highlight the differences between the FDTM and the theoretical solution, figure 6(b) gives the relative errors ${\rm \Delta} R/R_{{T}}$, where ${\rm \Delta} R=R_{{T}}-R_{{F}}$, $R_{{T}}$ and $R_{{F}}$ are the shock radii calculated by the theory and the FDTM, respectively. The shock front calculated by the FDTM essentially agrees with the theoretical solution. When the initial discrete points on the shock front with a spatial resolution of ${\rm \Delta} s_0/S_0=2.5\times 10^{-3}$, the evolution of the CMS can be accurately calculated by the FDTM with a relative error less than $4\,\%$. Therefore, the initial length of ${\rm \Delta} s_0/S_0=2.5\times 10^{-3}$ is used for all cases in the present study. To examine the characteristics calculated by the FDTM, any characteristic $C^+$ or $C^-$ can be used because the flow is axisymmetric. The characteristic $C^+$ originating from the endpoint of the initial shock front on the negative $z$-axis is shown in figure 6(c), which is compared with the theoretical characteristic solution solved directly using the characteristic relations. Similarly, figure 6(d) gives the relative errors ${\rm \Delta} y/y_{{T}}$ between the characteristic $C^+$ calculated by the FDTM and the theoretical solution, where ${\rm \Delta} y =y_{{T}}-y_{{F}}$, $y_{{T}}$ and $y_{{F}}$ are the ordinates calculated by the theory and the FDTM, respectively. Good agreement with a relative error less than $3\,\%$ is achieved in the shape of the characteristic when ${\rm \Delta} s_0/S_0=2.5\times 10^{-3}$. However, the time information is not contained in the theoretical characteristic solution, which cannot match the evolution of the shock front. Fortunately, the FDTM in the present study break through this limitation, which combines the evolution of the shock front with the disturbances on the shock front in real time. With the help of the FDTM, the evolution of the CMS can be further analysed as follows.

Figure 6. (a) Theoretical solution of the shock front radius ($R$) varying with time t and the results calculated by the FDTM with three sets of discrete points. (b) Relative errors ${\rm \Delta} R/R_{{T}}$ between the theoretical shock radii and those calculated by the FDTM. (c) Characteristic $C^+$ originating from the endpoint of the initial shock front on the negative $z$-axis calculated by the FDTM and the theoretical solution. (d) Relative errors ${\rm \Delta} y/y_{{T}}$ between the characteristic $C^+$ calculated by the FDTM and the theoretical solution for $M_\infty =6$, $AR=1.0$ and $\delta _0=10^\circ$.

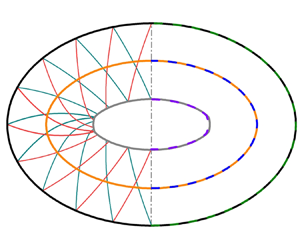
Figure 7 shows the instantaneous shock fronts at typical times of $t/T=0, 1.31$ and 2.62, on which a set of characteristics $C^+$ and $C^-$ in every 20 points are superimposed. All results are calculated by the FDTM with ${\rm \Delta} s_0/S_0=2.5\times 10^{-3}$. The initial CMS accompanies bidirectional disturbances, which propagate along the shock front during convergence to intensify the shock. Hence, those disturbances are shock–compression. Note that the intervals between any adjacent disturbances from the same family are equal in real time. In other words, those disturbances can be regarded as uniform disturbances, which guarantee that the CMS always maintains a circular shape. In short, the evolution of the CMS is equivalent to that of the axisymmetric ICS before the formation of the Mach disk.

Figure 7. Shock front at the time $t/T=0, 1.31$ and 2.62, characteristics $C^+$ and $C^-$ calculated by the FDTM with ${\rm \Delta} s_0/S_0=2.5\times 10^{-3}$ for $M_\infty =6$, $AR=1.0$ and $\delta _0=10^\circ$.

3.3.2. Convergence of the CMS with initial non-uniform intensity

As shown in § 3.3.1, when the initial shock Mach numbers along the CMS are the same, the converging shock always maintains a circular shape. However, the CMS is unstable to small disturbances (Whitham Reference Whitham1957). When the initial shock Mach number of the CMS is perturbed by a small value, the disturbances increase with the converging shock and thus, kinks appear and make the shock shape into straight segments (Schwendeman Reference Schwendeman1999). Similar behaviours were also observed in experiments (Takayama et al. Reference Takayama, Kleine and Grönig1987; Watanabe & Takayama Reference Watanabe and Takayama1991). To examine the accuracy of the FDTM in predicting the formation time and position of kinks, the evolution of a converging CMS with an initial perturbation in its intensity is adopted for validation. Since this specific case was numerically solved using GSD by Schwendeman (Reference Schwendeman1993, Reference Schwendeman1999), the same description of the problem is used here.

The initial shape of the CMS in the Cartesian coordinate system $(x,y)$ is

(3.9a,b)\begin{equation} x={\rm e}^{{-}r}\cos\left( 2 {\rm \pi}s\right),\quad y={\rm e}^{{-}r}\sin\left( 2 {\rm \pi}s\right), \end{equation}

where the initial radial distance $R_0={\rm e}^{-r}$ with $r=0$, and $s\in [0,1)$. The initial distribution of the shock Mach number $M_{{s0}}$ along the CMS is

(3.10)\begin{equation} M_{{s0}}=2+0.2\sin(10 {\rm \pi}s). \end{equation}

In the perspective of GSD, the disturbances induced by the initial non-uniformity in the shock intensities gradually increase and aggregate during the CMS convergence, which causes the shock shape to deviate from the circular shape and form kinks on the shock front.

Figure 8(a) shows the shock fronts calculated by the FDTM at typical time $T_n=0,0.32$ and $1.05$ with ${\rm \Delta} s_0 / S_0 =2.5 \times 10^{-3}$, on which a set of characteristics $C^+$ and $C^-$ in every $20$ points are superimposed and anticlockwise numbered as $1,2,\ldots,j$. With the help of FDTM, the evolution of the converging shock can be further analysed. The bidirectional shock–compression disturbances caused by the initial non-uniformity of the shock intensity unevenly propagate along the shock front (i.e. the characteristics), which plays a prominent role for the deformation and non-uniform intensification of the shock. As the shock converges, the interval between any adjacent shock–compression disturbances from the same family continuously decreases (see figure 8a). When the shock–compression disturbances from the same family intersect, the shock–compression disturbances transit to the shock–shock disturbance (Han & Yin Reference Han and Yin1993), which indicates the kink formation. Due to the five-fold circular symmetry of the initial perturbation in (3.10), five pairs of left-running and right-running shock–shocks (i.e. 10 kinks) on the converging shock front are formed simultaneously, which divides the converging shock front into 10 shock segments at $T_n=1.05$. Specifically, the intersection point between the characteristics $C_1^-$ and $C_2^-$ in the enlarged view of figure 8(a) is $(x/R_0,y/R_0)=(0.2131,-0.2346)$, which is the formation position of the kink. The shock fronts calculated by Schwendeman (Reference Schwendeman1999) are also superimposed on figure 8(a), where the formation position of the kink is $(x/R_0,y/R_0)=(0.2130,-0.2345)$. Thus, the relative error of the kink formation positions is less than $0.1\,\%$. Furthermore, when the converging shock front passes the circle with a radius of ${\rm e}^{-r}$ and $r = 0.5$ (i.e. the grey dotted line in figure 8a before the kink formation), Schwendeman (Reference Schwendeman1999) provided the shock Mach numbers. These shock Mach numbers are compared with those calculated by the FDTM in figure 8(b), which yields a relative error less than $3\,\%$ at the peak and trough positions. Thus, the FDTM can well predict the evolution of the converging CMS with an initial non-uniformity in its intensity.

Figure 8. (a) Evolution of the shock front and characteristics. (b) Comparison of shock Mach numbers when the shock passes the circle with a radius of ${\rm e}^{-r}$ and $r = 0.5$.

For the converging CMS with a large $M_{{s0}}$ and a sufficiently small perturbation, an asymptotic solution for the kink formation time $T_{{K}}$ and the corresponding shock radius $R_{{K}}$ was derived by Mostert et al. (Reference Mostert, Pullin, Samtaney and Wheatley2018b), which is adopted here to further illustrate the performance of the FDTM. The initial shape of the CMS satisfies (3.9a,b), while the initial distribution of the shock Mach numbers is consistent with that of Mostert et al. (Reference Mostert, Pullin, Samtaney and Wheatley2018b), which can be expressed as

(3.11)$$\begin{gather} M_{{s0}}=20[ 1 +q \epsilon \sin( 2 {\rm \pi}qs)]^{{-}1/n}, \end{gather}$$

(3.12)$$\begin{gather}n=1+\frac{2}{\gamma}+\left( \frac{2 \gamma}{\gamma-1}\right)^{1/2}, \end{gather}$$

where $2{\rm \pi} /q$ is periodic over CMS with a wavenumber $q=8$, and $\epsilon$ is a perturbation amplitude, and $\gamma =5/3$. The cases with $q^2\epsilon =0.16,0.32,0.64,0.96,1.28$ and $1.6$ are calculated by the FDTM, and the corresponding formation time of the kinks are extracted for comparisons with the literature.

The kink formation time $T_{{K}}$ and the corresponding shock radius $R_{{K}}$ calculated by the FDTM are shown in figures 9(a) and 9(b), respectively, where the abscissa and ordinate are displayed in logarithms. The asymptotic solution reported by Mostert et al. (Reference Mostert, Pullin, Samtaney and Wheatley2018a,Reference Mostert, Pullin, Samtaney and Wheatleyb) using the nonlinear Fourier-based analysis method, and the numerical results obtained by the method of Schwendeman (Reference Schwendeman1993) using GSD are superimposed on figure 9. It is obvious that $T_{{K}}$ and $R_{{K}}$ calculated by the FDTM agree well with the numerical results reported by Schwendeman (Reference Schwendeman1993). Both of them approach the asymptotic solution as $q^2 \epsilon$ decreases. In other words, the formation of a kink in the limit $q^2 \epsilon \longrightarrow 0$ is suggested by the asymptotic solution, which is in support of the results calculated by the FDTM.

Figure 9. (a) Comparisons of the kink formation time $T_{{K}}$ for $M_{{s0}}=20$, $q=8$ and $\gamma =5/3$. (b) Comparisons of shock radius $R_{{K}}$ at the kink formation for $M_{{s0}}=20$, $q=8$ and $\gamma =5/3$.

In short, the collapse of a CMS with an initial non-uniformity in its intensity can be solved by the FDTM with sufficient accuracy. Undoubtedly, once the converging CMS deviates from the axisymmetric state to be an EMS that is equivalent to an elliptical ICS, kinks also appear on the shock front. With the help of FDTM, it is valuable to address the evolution mechanisms of the elliptical ICS, which is discussed in § 4.

4.2.1. Convergent behaviours of the equivalent EMS

The convergent behaviours of the equivalent EMS are calculated by the FDTM with ${\rm \Delta} s_0/S_0=2.5\times 10^{-3}$, in which the propagation trajectories of the disturbances (i.e. characteristics $C^+$ and $C^-$) emitted from the initial shock front are tracked in real time. The instantaneous shock fronts at typical times of $t/T=0, 0.798$ and 1.596 are shown in figure 11(a), on which a set of characteristics $C^+$ and $C^-$ in the upper half-plane every 20 points are superimposed and anticlockwise numbered as $0,1,\ldots,j$ from the positive $z$-axis. When the shock converges to time $t/T=1.596$, the termination criterion of the calculation in the FDTM is met, which indicates that the characteristics in the same family intersect to form kinks. Due to the geometric symmetry, four kinks concurrently appear on the shock front at ($y/a,z/a)=(\pm 0.396,\pm 0.047)$, which divide the shock front into two pairs of arch-shaped shock segments.

Figure 11. (a) Evolution of the shock front and characteristics, where dashed lines are the results of Computational Fluid Dynamics (CFD). (b) Circumferential distribution of the pressure ratio in the evolution of the shock for $AR=1.43$ when $\delta _0=10^{\circ }$ and $M_\infty =6$, where solid points are the results of Computational Fluid Dynamics (CFD).

For comparison, a 3-D Euler solver based on the finite volume method was employed to simulate the 3-D steady elliptical flow field, in which the effects of viscosity and the presence of a boundary layer on the shock front were deemed negligible (Zhang et al. Reference Zhang, Li, Ji, Si and Yang2021). The computational domain, boundary conditions, numerical schemes, etc., adopted for all 3-D validation cases in this paper are consistent with the numerical simulations conducted by Zhang et al. (Reference Zhang, Li, Ji, Si and Yang2021). In short, this solver has been demonstrated reliable in our previous studies (Zhang et al. Reference Zhang, Li, Ji, Si and Yang2021; Ji et al. Reference Ji, Li, Zhang, Si and Yang2022), in which it captured complex shock structures well. The equivalent shock fronts on $x/a=0, 0.798$ and 1.596 are extracted from the 3-D numerical simulation (Zhang et al. Reference Zhang, Li, Ji, Si and Yang2021) and superimposed on the lower half-plane in figure 11(a), where the formation positions of kinks are ($y/a,z/a)=(\pm 0.387,\pm 0.050)$. As the relative difference in the kink positions between the FDTM and the 3-D numerical simulation is less than $6\,\%$, the evolution of the shock fronts calculated by the FDTM essentially agrees with the previous 3-D numerical simulation under the premise of equivalence. It must be emphasized that the FDTM can rapidly and quantitatively determine the evolution of the shock fronts and the formation positions of kinks with significantly lower cost than the 3-D numerical simulation. Moreover, figure 11(b) compares the circumferential distributions of the pressure ratio ($p/p_\infty$) across the shock (i.e. the shock intensity) calculated by the FDTM and the 3-D numerical simulation, where the shock intensity distributions of the equivalent EMS are calculated by the oblique shock relationship,

(4.2)\begin{equation} \frac{p}{p_\infty}=1+\frac{2\gamma}{\gamma+1}\left\lbrace M_\infty^2\sin^2 \left[\arctan\left( \frac{M_{{s}}}{M_\infty} \right)\right] -1\right\rbrace, \end{equation}

where $p_\infty$ is the pressure ahead of the shock. As shown in figure 11(b), the shock intensities calculated by the FDTM are also in good agreement with those of the 3-D numerical simulation. Although the initial elliptical shock has a circumferentially uniform intensity, the shock intensities near the major axis ($\varphi = 90^{\circ },270^{\circ }$) significantly increase with shock convergence. As a result, kinks are formed near the major axis, which not only indicate the discontinuity of the shock front but also indicate a sharp change in the shock intensity. With the help of the FDTM, the evolution of the EMS can be further analysed. As shown in the upper half-plane in figure 11(a), the initial elliptical shock front accompanies a series of bidirectional shock–compression disturbances (Whitham Reference Whitham1957, Reference Whitham1958), which unevenly propagate along the shock front and play a prominent role in shock intensification. As tracked by the characteristics, the interval between any adjacent disturbances from the same family continuously decreases. Particularly, the disturbances near the major axis become denser (see figure 11a), indicating that the local shock intensity enlarges significantly (see figure 11b). When the moving shock converges to $t/T=1.596$, the disturbances from the same family initially near the major axis (e.g. the characteristic $C_4^-$ in figure 11a) catch up with the disturbance emitted from the major axis (i.e. the characteristic $C_5^-$ in figure 11a). Thus, the disturbances transform from the shock–compression into the shock–shock (Han & Yin Reference Han and Yin1993), which leads to the formation of kinks (see the enlarged view in figure 11a). However, a puzzling phenomenon is that the disturbances from the same family initially near the major axis determine the formation of kinks rather than the rest of the disturbances, which is clarified as follows.

4.2.2. Propagation of the disturbances

The propagation of the disturbances can be quantitatively analysed using the FDTM because the characteristics calculated by the FDTM are endowed with time information. Considering the geometric symmetry of the EMS, the characteristics $C^-$ initially within the circumferential angle $\varphi = 0^{\circ }$ to $90^{\circ }$ numbered $0$ to $5$ (i.e. $C_0^-$ to $C_5^-$) in figure 11(a) are selected to clarify the intersection of the disturbances from the same family, where $\varphi$ is the angle between the disturbance position and the positive $z$-axis, $C_0^-$ is initially emitted from the minor axis, and $C_5^-$ is initially emitted from the major axis. As shown in figure 12, the variation of $\varphi$ on the characteristics $C_0^-$ to $C_5^-$ with time $t$ are extracted from the FDTM. For comparison, the characteristic $C^-$ of the CMS generated by the ring wedge with the same $\delta _0$ (see figure 7) is superimposed on figure 12. Due to the circumferential symmetry of the disturbance's propagation on the CMS, only the characteristic $C_0^-$ initially emitted from the positive $z$-axis (i.e. $\varphi = 0^{\circ }$) is shown in figure 12.

Figure 12. Variation of circumferential angle $\varphi$ of characteristics $C^-$ with time $t$ for $AR=1.43$ when $\delta _0=10^{\circ }$ and $M_\infty =6$.

As the shock converges to the centre, both the value and the growth rate of $\varphi$ (i.e. the slope of the $\varphi -t$ curve) on the characteristic $C^-$ increase gradually on the CMS (see figure 12). Note that the variation in $\varphi$ remains the same for each disturbance on the CMS, and thus, they cannot catch up with each other. However, the variations of $\varphi$ on the characteristics $C^-$ emitted from different initial positions on the EMS change considerably. As shown in figure 12, the $\varphi$ of the characteristics initially near the minor axis (e.g. $C_0^-$ and $C_1^-$) increase significantly, whereas the $\varphi$ of the characteristics initially near the major axis (e.g. $C_4^-$ and $C_5^-$) increase slowly. Although the growth rates of $\varphi$ vary with the initial positions on the EMS, the $\varphi$ of the characteristics $C_0^-$ to $C_4^-$ always increase with time. It is evident that the variation tendency of $\varphi$ on the characteristic $C_5^-$ reverses following the initial increase. In other words, the variation in $\varphi$ on the characteristic $C_5^-$ is non-monotonic. The abnormal behaviour of the characteristic $C_5^-$ enables the characteristics initially near the major axis to first catch up with it. When the $\varphi$ of the characteristics $C^-$ initially emitted from different positions reaches the same value (see $C_4^-$ and $C_5^-$ in figure 12), the gathered shock–compression disturbances turn into a shock–shock disturbance (Han & Yin Reference Han and Yin1993), which causes the formation of a kink on the shock front within $\varphi >90^\circ$. Note that the characteristics $C^+$ and $C^-$ are strictly symmetric about the major axis (i.e. $\varphi =90^\circ$) rather than the $C^-$ themselves. Thus, another kink forms simultaneously on the shock front within $\varphi <90^\circ$ (see figure 11a).

To better understand the variations in $\varphi$ on the characteristics, the propagation speed of the disturbance is further calculated. Taking the characteristic $C_j^-$ as an example, the decomposition schematic of the propagation speed of the disturbance is shown in figure 13, where $O$ is the geometric centre of the EMS and $O'$ is the position of the disturbance on the shock front at time $t$. Both the propagation speed $u$ of the disturbance along the shock front and the convergence speed $w$ (along the ray) of the shock front cause the variation of $\varphi$, where $u$ and $w$ are determined by the following, respectively (Han & Yin Reference Han and Yin1993):

(4.3)$$\begin{gather} u=c_0 \left[ \frac{1}{2}{(M_{{s}}^2-1)K(M_{{s}})}\right]^{1/2}, \end{gather}$$

(4.4)$$\begin{gather}w=c_0M_{{s}}. \end{gather}$$

Obviously, $u$ and $w$ are positively correlated with the local shock Mach number $M_{{s}}$ on the shock front, in which $u$ is always less than $w$ (Han & Yin Reference Han and Yin1993). The angular speeds induced by $u$ and $w$ in the polar coordinate system are $\omega _1$ and $\omega _2$, respectively:

(4.5)$$\begin{gather} \omega_1=\frac{u\cos(\xi)}{r}; \end{gather}$$

(4.6)$$\begin{gather}\omega_2=\frac{w\sin(\xi)}{r}; \end{gather}$$

where $O$ is the pole, the positive $z$-axis is the polar axis, $r$ is the polar radius of the disturbance $O'$, and $\xi$ is the angle between the ray and the polar radius $OO'$. Thus, the circumferential angular speed of the disturbance on the characteristics $\omega$ is

(4.7)\begin{equation} \omega=\omega_1+\omega_2. \end{equation}

Note that $\omega _1$ is always positive, whereas $\omega _2$ can be positive, zero, or negative depending on $\xi$. It is evident that $\xi$ always equals zero for the CMS, and thus, $\omega = \omega _1$ on the CMS. In other words, the convergence speed of the CMS does not change the value of $\varphi$. However, the variations in $\omega$ on the characteristics $C^-$ on the EMS are complicated. When the characteristic $C^-$ does not cross the major axis (i.e. $\varphi < 90^{\circ }$), $\xi$ is positive, and thus, $\omega _1$ and $\omega _2$ are in the same direction to increase $\varphi$. Once the characteristic $C^-$ crosses the major axis (i.e. $\varphi > 90^{\circ }$), $\xi$ is negative, and thus, $\omega _1$ and $\omega _2$ are in the opposite directions, in which $\omega _2$ decreases $\varphi$. Note that the values of $\xi$, $u$ and $w$ are closely related to the position of the disturbance on the shock front, which is responsible for the complicated changes in $\omega$.

Figure 13. Decomposition of the propagation speed of the disturbance on the shock.

As shown in figure 14, the variations in $\omega$ extracted from the FDTM are further analysed with time $t$, which can explain the behaviours of $\varphi$ in figure 12. For comparison, the $\omega = \omega _1$ of the characteristic $C_0^-$ on the CMS is superimposed on figure 14. As the circumferentially uniform $\omega _1$ increases with the strength of the CMS, $\varphi$ also increases monotonically on the CMS (see figure 12). However, the variations in $\omega$ on the characteristics $C^-$ initially emitted from different positions on the EMS are asynchronous. Although the circumferential strength of the initial elliptical shock front is the same at $t=0$, the initial $\omega$ is not uniform due to the shock front deviating from the circular shape. From the minor axis to the major axis, the initial $\omega$ of the characteristics on the EMS increase and then decrease, in which the initial $\omega$ of $C_5^-$ emitted from the major axis is the smallest but equal to that on the CMS. As the shock converges and strengthens, the $\omega$ on the characteristics initially near the minor axis (e.g. $C_0^-$ and $C_1^-$) increase monotonically (see figure 14). Therefore, the $\varphi$ on the characteristics $C_0^-$ and $C_1^-$ increase significantly (see figure 12). Although the $\omega$ on the characteristics $C_2^-$ to $C_4^-$ change non-monotonically, first increasing and then decreasing, they are always positive (see figure 14). Thus, the $\varphi$ on the characteristics $C_2^-$ to $C_4^-$ continues to increase (see figure 12). Interestingly, the $\omega$ on the characteristic $C_5^-$ decreases with time following the initially slight increase (see figure 14). As the characteristic $C_5^-$ crosses the major axis at the beginning, $\omega _1$ and $\omega _2$ change in the opposite directions, which turns $\omega$ negative once $\omega _2 < -\omega _1$. After that turning point, the variation of $\varphi$ on the characteristic $C_5^-$ reverses, which creates a key condition for the characteristics initially near the major axis to first catch up with $C_5^-$. In other words, kinks inevitably appear on the characteristic initially emitted from the major axis.

Figure 14. Variation of circumferential angular speed $\omega$ with time $t$ for $M_\infty =6$, $AR=1.43$ and $\delta _0=10^\circ$.

The characteristics $C^-$ originating from $\varphi >90^\circ$ (e.g. $C_6^-$ to $C_9^-$ in figure 11a) are further analysed to comprehensively understand the propagation of disturbances on the EMS. Near the major axis, the variation of $\varphi$ on the characteristics $C^-$ originating from $\varphi >90^\circ$ (e.g. $C_6^-$ to $C_7^-$ in figure 11a) are slower than that of the characteristic $C^-$ originating from the endpoint of the major axis (i.e. $C_5^-$), which can be revealed by the change in $\omega$. Note that $\omega _1$ and $\omega _2$ are in the opposite directions at the beginning for the characteristics $C^-$ originating from $\varphi >90^\circ$, which is different from $\omega _1$ together with $\omega _2$ in the promotion of $\varphi$ on the characteristics $C^-$ originating from $\varphi <90^\circ$. In the early stage of shock convergence, the competition between $\omega _1$ and $\omega _2$ yields a smaller positive $\omega$ on the characteristics $C^-$ originating from $\varphi >90^\circ$. Thus, $\varphi$ on the characteristics $C^-$ originating from $\varphi >90^\circ$ slightly increases. As the shock converges and strengthens, $\omega$ changes from positive to negative, causing a slow decline in $\varphi$ (e.g. $C_6^-$ to $C_7^-$ in figure 11a). It seems that the variation of $\varphi$ in $C_6^-$ gives an opportunity for $C_5^-$ to catch up with $C_6^-$, but $C_4^-$ originating from $\varphi <90^\circ$ intersects with $C_5^-$ much earlier because $\omega$ of $C_4^-$ is always positive (see figure 14). For the characteristics $C^-$ far away from the major axis (e.g. $C_7^-$ to $C_9^-$ in figure 11a), the initial angular difference between the adjacent characteristics and the variations of $\varphi$ on them make it impossible for the adjacent characteristics to intersect. In short, the characteristics $C^-$ originating from $\varphi \leq 90^\circ$ near the major axis determine the formation of kink at $\varphi =97.27^\circ$ rather than the characteristics $C^-$ originating from $\varphi >90^\circ$. Since the characteristics $C^+$ and $C^-$ are strictly symmetric about the major axis, the characteristics $C^+$ originating from $\varphi \geq 90^\circ$ near the major axis simultaneously form another kink at $\varphi =82.73^\circ$.

In summary, the FDTM can rapidly predict the positions and reveal the mechanisms of kink formation in a 3-D steady elliptical ICS from the perspective of GSD. In fact, the formation position of kinks in the flow direction is significantly affected by the elliptical entry aspect ratio $AR$ (Zhang et al. Reference Zhang, Li, Ji, Si and Yang2021), which can be thoroughly studied using the FDTM.

4.3.1. Effects of $AR$ on kinks of the equivalent EMS

The propagations of the characteristics $C^+$ and $C^-$ initially emitted from the endpoints of the major axis dominate the formation positions of kinks on the equivalent EMS (see § 4.2). Considering the symmetry of the disturbance's propagation on the equivalent EMS, only the characteristic $C_5^-$ initially emitted from the endpoint of the major axis is extracted until a kink forms on it, according to the results predicted by the FDTM with ${\rm \Delta} s_0/S_0=2.5\times 10^{-3}$. Thirty-three elliptical ring wedges with the same conditions of $\delta _0=10^{\circ }$ and $M_\infty =6$ are selected by equidistantly changing $b$ within the range of $20\ {\rm mm} \leq b \leq 85\ {\rm mm}$, which yields different $AR{\rm s}$ ranging from 1.18 to 5.00. To be sure, all elliptical ring wedges are in the conservative area in figure 10 (i.e. $\lambda _{{M}} < \lambda _{{N}}$).

Figure 15 shows the variations of $\omega$ on the characteristic $C_5^-$ with typical $AR{\rm s}$ listed in table 1, where the abscissa of the propagation time $t/T$ of $C_5^-$ is displayed in logarithms starting from $10^{-3}$ to enlarge the behaviour of $C_5^-$ in the early stage. Although all $\omega$ on $C_5^-$ for different $AR{\rm s}$ are the same at the initial time, the propagation process of $C_5^-$ changes significantly for different $AR{\rm s}$, which affects the formation position of the kink on the equivalent EMS. When the initial deviation of the shock front from the CMS is small, such as $AR=1.18, 1.25$ and 1.43, the propagation of $C_5^-$ along the shock front dominates the variation of $\omega$ in the early stage rather than the convergence effect of the shock front itself. In other words, the gain of $\omega _1$ induced by the propagation speed $u$ of the disturbance along the shock front overcomes the loss of the angular speed $\omega _2$ induced by the convergence speed $w$ of the shock front itself (see figure 13). Thus, $\omega$ of $C_5^-$ grows at the first stage for these relatively small $ARs$ (see the close-up view of figure 15). As the equivalent EMS converges towards the centre, the convergence effect of the shock front itself enhances rapidly, which causes the $\omega$ of $C_5^-$ to decrease sharply. Moreover, the time taken for the growth stage of $\omega$ shortens with the increase in $AR$. In contrast, for large $AR{\rm s}$, such as $AR=2.00, 3.50$ and 5.00, the convergence effect of the shock front itself plays a dominant role in the variation of $\omega$ rather than the propagation of $C_5^-$ along the shock front, which causes the $\omega$ of $C_5^-$ to decrease at the beginning (see the close-up view of figure 15). When the $\omega$ of $C_5^-$ decreases to a negative value, the characteristic $C^-$ initially close to the major axis catches up with $C_5^-$ easier to form the kink on $C_5^-$. As shown in figure 15, kinks form earlier on the EMS as $AR$ increases.

Figure 15. Variation of $\omega$ on the characteristic $C_5^-$ with time $t$ for typical $AR{{\rm s}}$ when $\delta _0=10^{\circ }$ and $M_\infty =6$.

To better understand the evolution of the kink on the EMS with different $AR{\rm s}$, the formation time $t_{{K}}$ and position ($r_{{K}},\varphi _{{K}}$) of the kink are extracted from the endpoint of $C_5^-$ and shown in figures 16(a) and 16(b), respectively. It is evident that $t_K$ decays with the increase in $AR$, in which $t_{{K}}$ shows asymptotic behaviour following a sharp decrease for $AR$ approximately less than 2 (see figure 16a). Similarly, $r_{{K}}$ and $\varphi _{{K}}$ also asymptotically approach different values with the increase in $AR$ (see figure 16b). Moreover, the variation of $r_{{K}}$ and $\varphi _{{K}}$ exhibit opposite trends, which indicates that the formation position of the kink is closer to the major axis and farther away from the convergence centre with the increase in $AR$. As kinks on the equivalent EMS are already calculated by the FDTM, the formation positions of kinks on the 3-D steady elliptical ICS in the flow direction (i.e. $x$) can be predicted according to (2.2), while the formation positions of kinks in the cross-section of the elliptical ICS are ideally the same as those on the equivalent EMS. Note that the accuracy of the equivalent formation positions of kinks for different $AR{\rm s}$ needs to be examined.

Figure 16. (a) Variation of the kink's formation time $t_{{K}}$ with $AR$. (b) Variation of the kink's formation position $r_{{K}}$ and $\varphi _{{K}}$ with $AR$ on the equivalent EMS when $\delta _0=10^{\circ }$ and $M_\infty =6.0$.

4.3.2. Equivalence of the kinks at different $AR$

It is worth briefly reviewing the evolution of the 3-D steady elliptical ICS before examining the equivalent formation positions of kinks. As reported by Zhang et al. (Reference Zhang, Li, Ji, Si and Yang2021), the initial strength of the elliptical ICS is the same on the circumference, but the non-uniform intensification effects on the circumference drive the initially smooth shock surface to be discontinuous as the formation of kinks on the shock surface. The kinks separate the shock surface into two pairs of shock segments, including one stronger pair around the major axis and the other weaker pair around the minor axis, both of which propagate towards the centreline. Therefore, four kink trajectories are inevitably created on the elliptical ICS surface (see figure 1a). Correspondingly, the kinks in the equivalent 2-D unsteady flow are not stable shock anchoring. It is well demonstrated by the typical case of $AR=1.43$ in § 4.2 that the FDTM can quickly reproduce the process of the 3-D elliptical ICS from the initially smooth shock front to kink formation from the equivalent 2-D unsteady perspective, although the FDTM is not yet sufficient to predict the propagation of the shock segments after the formation of kinks. For a wide range of $AR{\rm s}$, the equivalence of the kink's formation position predicted by the FDTM needs further verification.

Figure 17 shows the shock front (i.e. the black dashed line) with the formation of kinks (i.e. blue dots) on the EMS calculated by the FDTM for typical $AR{\rm s}$ listed in table 1, in which the formation time of kinks is marked as $t_{{K}}/T$. For comparison, the normalized density contours in the equivalent cross-section $x_{{KT}}/a=V_\infty t_{{K}}/a$ of the 3-D elliptical ICS are superimposed on the upper half-plane of figure 17. Surprisingly, the shock front including the kinks’ positions at time $t_{{K}}/T$ (i.e. the black dashed line) differs obviously from that of the equivalent cross-section $x_{{KT}}/a$ (i.e. the purple line) of the 3-D elliptical ICS for small $AR{\rm s}$ shown in the upper half-planes of figures 17(a) and 17(b). Actually, the discontinuous points on the equivalent cross-section $x_{{KT}}/a$ of the 3-D elliptical ICS (i.e. pink dots in figure 17) are not the formation positions of kinks, but rather the points on the kink trajectories after the kink formation. As $AR$ increases, e.g. $AR = 1.43$ and 2, kinks form earlier on the EMS, and the difference in the shock front between the time $t_{{K}}/T$ and the equivalent cross-section $x_{{KT}}/a$ shrinks significantly (see the close-up view of figures 17c and 17d). Particularly, the difference in the shock front, including the kink positions, is indistinguishable for $AR=5.0$ (see the enlarged view in figure 17e). The comparisons in the upper half-planes of figure 17 indicate that the shock front with the formation of kinks calculated by the FDTM is always larger than that of the equivalent cross-section on the 3-D elliptical ICS for different $AR{\rm s}$. It seems that the spatial evolution of the 3-D elliptical ICS is faster than the temporal evolution of the equivalent EMS predicted by the FDTM, but the evolutions of the shock front are similar to each other (see figure 17). The difference between them is caused by a mismatch in the $x$ direction.

Figure 17. Comparison of the kink formation position between the EMS and the 3-D elliptical ICS for typical $AR{\rm s}$ listed in table 1 when $\delta _0=10^{\circ }$ and $M_\infty =6$: (a) $AR=1.18$; (b) $AR=1.25$; (c) $AR=1.43$; (d) $AR=2.00$; (e) $AR=5.00$.

To quantify the difference in the kink formation position in the $x$ direction, one can look for a cross-section $x_{{K}}/a$ on the 3-D elliptical ICS upstream of $x_{{KT}}/a$, on which the shock front including the kink positions are almost identical to those calculated by the FDTM at $t_{{K}}/T$. The cross-sections $x_{{K}}/a$ on the 3-D elliptical ICS for different $ARs$ are superimposed on the lower half-planes of figure 17, which are considered the kink formation positions on the 3-D elliptical ICS. The differences between $x_{{KT}}$ predicted by the FDTM and the real position $x_{{K}}$ on the 3-D elliptical ICS are listed in table 2. As expected, the difference between $x_{{KT}}$ and $x_{{K}}$ gradually decreases with the increase in $AR$. For $AR$ greater than 1.43, $(x_{{KT}}-x_{{K}})/x_{{KT}}$ is less than $1\,\%$ (see table 2), and the kink formation positions on the $x_{{KT}}$ cross-section predicted by the FDTM are extremely close to the real positions on the 3-D elliptical ICS (see the upper half-planes of figure 17c–e). Although the difference between $x_{{KT}}$ and $x_{{K}}$ increases for small $AR{\rm s}$, $(x_{{KT}}-x_{{K}})/x_{{KT}}$ is only approximately $3\,\%$ even for the smallest $AR=1.18$ (see table 2). An interesting question is why a slight difference between $x_{{KT}}$ and $x_{{K}}$ for small $AR{\rm s}$ causes a significant difference in the shock front and the kink formation positions (see the upper half-planes of figure 17a,b),which needs to be addressed. It is of great importance to accurately and quickly determine the kink formation positions on the elliptical ICS using the FDTM, once the results predicted by the FDTM can be improved.

Table 2. Differences in the kink formation position calculated by the FDTM and the 3-D numerical simulations.

4.3.3. Modification of the kink formation position in the $x$ direction

The reason for the difference in the kink formation position between the equivalent EMS and the 3-D elliptical ICS is discussed by seeking the evolution of the shock angle $\lambda _{{M}}$ along the $x$ direction. When the $\lambda _{{M}}$ of the EMS and the 3-D elliptical ICS are the same, the shape of the shock front is almost consistent with that of the 3-D elliptical ICS. While the horizontal spacing ${\rm \Delta} x$ of the same $\lambda _{{M}}$ reflects the difference in the shock front in the $x$ direction between the equivalent EMS and the 3-D elliptical ICS.

Since the symmetry of the shock front and the kink formation positions are near the major axis, only the shock angle $\lambda _{{M}}$ in the upper half of the major plane (i.e. the slope of the shock front along the $x$ direction) calculated by the FDTM and the 3-D numerical simulations for typical $AR{\rm s}$ are compared in figure 18(a). The $\lambda _{{M}}$ in the major plane of the 3-D elliptical ICS is obtained spontaneously using the 3-D numerical simulations, while the abscissa $x/a$ and $\lambda _{{M}}$ on the equivalent EMS are calculated by (2.2) and (4.1), respectively. The cut-off positions of the equivalent EMS and the 3-D elliptical ICS in figure 18(a) correspond to $x_{{KT}}/a=V_\infty t_{{K}}/a$ and $x_{{K}}/a$, respectively. Moreover, the $\lambda _{{M}}$ of the axisymmetric ICS (i.e. $AR=1.00$) and the equivalent CMS with the theoretical solution are superimposed in figure 18(a) as a pair of limit cases without kinks, where the cut-off position in the axisymmetric ICS corresponds to the Mach disk.

Figure 18. (a) Variation of the shock front $\lambda _{{M}}$ in the upper half of the major plane along the $x$ direction calculated by the FDTM and the 3-D numerical simulation for typical $AR{\rm s}$. (b) Variation of the ${\rm \Delta} x$ with $\lambda _{{M}}$ for typical $AR{\rm s}$ when $\delta _0=10^{\circ }$ and $M_\infty =6$.

As shown in figure 18(a), the initial $\lambda _{{M}}$ for different $AR{\rm s}$ are the same due to the identical leading-edge angle $\delta _0$ and $M_\infty$. The results of the CMS calculated by the FDTM are consistent with the theoretical solution by Hornung et al. (Reference Hornung, Pullin and Ponchaut2008) (see figure 18a), indicating that the FDTM can accurately calculate the evolution of the moving shock. Nevertheless, discrepancies still exist when compared with the equivalent axisymmetric ICS (see figure 18a). Thus, the difference between the equivalent moving shock and the 3-D steady ICS is caused by the hypersonic equivalence principle itself rather than the FDTM. In fact, the applicability of the hypersonic equivalence principle decays as the shock strengthens along the $x$ direction (see § 2.2), which indicates that the accuracy of the equivalence depends on the change in $\lambda _{{M}}$. In other words, the horizontal spacing ${\rm \Delta} x$ of the same $\lambda _{{M}}$ between the equivalent moving shock and the 3-D steady ICS varies with $\lambda _{{M}}$, which is extracted in figure 18(b).

As shown in figure 18(b), the difference ${\rm \Delta} x$ between the equivalent CMS and the axisymmetric ICS gradually enlarges as $\lambda _{{M}}$ increases. Undoubtedly, the ${\rm \Delta} x$ in the cut-off position between the equivalent CMS and the axisymmetric ICS is the largest (see figure 18a). However, the $\lambda _{{M}}$ in the cut-off position of the elliptical ICS decreases with the increase in $AR$ (see figure 18a), resulting in a rapid decrease in ${\rm \Delta} x$ at the cut-off position (see figure 18b). Note that for small $AR$, e.g. $AR=1.25$, the $\lambda _{{M}}$ in the cut-off position is still large (see figure 18a), indicating a steep rise in the shock surface of the elliptical ICS. Therefore, a small difference between $x_{{KT}}$ and $x_{{K}}$ (see $AR=1.25$ in table 2) can lead to a discernible distinction in the shock front including the kink positions (see figure 17b).

Interestingly, the variation of ${\rm \Delta} x$ with $\lambda _{{M}}$ for the elliptical ICS is almost consistent with that of the axisymmetric ICS (see figure 18b). Thus, once the relationship between ${\rm \Delta} x$ and $\lambda _{{M}}$ on the equivalent CMS is known in advance, it can be used to improve the kink formation position predicted by the FDTM for different $AR{\rm s}$ . The variation of ${\rm \Delta} x$ with $\lambda _{{M}}$ on the equivalent CMS in figure 18(b) is easily obtained, which can be approximated by

(4.8)\begin{equation} \frac{{\rm \Delta} x(\lambda_{{M}})}{a}={\rm B}_1+{\rm B}_2 \exp({[(\lambda_{{M}}-\lambda_0)/{\rm B}_3]}),\quad \lambda_{{M}} > \lambda_0, \end{equation}

where $\lambda _0$ is the initial shock angle on the elliptical ICS, and the coefficients ${\rm B}_1=9.7 \times 10^{-4}$, ${\rm B}_2=2.6 \times 10^{-4}$ and ${\rm B}_3=2.2$. When the kink formation time $t_{{K}}$ and $\lambda _{{M}}$ in the cut-off position are calculated by the FDTM for a given $AR$, the modified equivalent kink formation position in the $x$ direction is $x'_{{KT}}/a=( V_\infty t_{{K}}-{\rm \Delta} x(\lambda _{{M}})) /a$. The relative errors $(x'_{{KT}}-x_{{K}})/x'_{{KT}}$ for $AR=1.18,1.25,1.43,2.00$ and $5.00$ are $0.44\,\%,0.26\,\%,0.16\,\%,0\,\%$ and $-0.01\,\%$, respectively. Compared with table 2, the modified $x'_{{KT}}$ is much closer to the real flow position $x_{{K}}$ on the 3-D elliptical ICS, which is less than $0.5\,\%$. Thus, the modification is helpful to more accurately and quickly determine the kink formation positions on the 3-D elliptical ICS using the FDTM.