Published online by Cambridge University Press: 25 May 2021
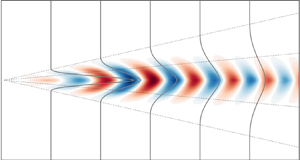
Coherent structures in the far field of a round turbulent jet are investigated experimentally and modelled by local linear stability analysis (LSA) and local resolvent analysis (RA). The study aims to determine the potential and limitations of mean flow-based linear models predicting the far field dynamics. Particular emphasis is placed on the high wavenumber and frequency range. The study is based on time-resolved stereoscopic particle image velocimetry (PIV) data acquired in the self-similar region of the jet. Spectral proper orthogonal decomposition (SPOD) is applied to the dataset to identify empirical coherent structures with azimuthal wavenumbers ranging from  $m=0$ to
$m=0$ to  $m=\pm 5$. The leading SPOD mode features low-rank behaviour over a wide frequency range and is found to account for the major part of total turbulent production. Thus, the leading SPOD mode captures the anisotropic part of turbulence, which is still significant even at the highest resolved frequencies reaching into the inertial subrange. The LSA determines stable but discrete eigenmodes that are excellently in line with the SPOD modes. This applies especially to modes at mid-range to high frequencies and higher azimuthal wavenumbers where the LSA predicts strongly decaying modes. Moreover, the RA modes are in very good agreement with LSA and SPOD modes, indicating a predominantly resonant mechanism. The present study shows that an unexpectedly wide range of turbulent scales in the self-similar region of the jet can be reproduced based on linearized mean-field models.
$m=\pm 5$. The leading SPOD mode features low-rank behaviour over a wide frequency range and is found to account for the major part of total turbulent production. Thus, the leading SPOD mode captures the anisotropic part of turbulence, which is still significant even at the highest resolved frequencies reaching into the inertial subrange. The LSA determines stable but discrete eigenmodes that are excellently in line with the SPOD modes. This applies especially to modes at mid-range to high frequencies and higher azimuthal wavenumbers where the LSA predicts strongly decaying modes. Moreover, the RA modes are in very good agreement with LSA and SPOD modes, indicating a predominantly resonant mechanism. The present study shows that an unexpectedly wide range of turbulent scales in the self-similar region of the jet can be reproduced based on linearized mean-field models.