Hostname: page-component-7479d7b7d-k7p5g Total loading time: 0 Render date: 2024-07-10T19:31:56.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability and weakly nonlinear analysis of the flow past rotating spheres

Published online by Cambridge University Press:  18 October 2016

V. Citro ,
J. Tchoufag ,
D. Fabre ,
F. Giannetti  and
P. Luchini
V. Citro*
Affiliation:
DIIN, Universitá degli Studi di Salerno, Via Giovanni Paolo II, 84084 Fisciano (SA), Italy
J. Tchoufag
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse); Allée Camille Soula, F-31400 Toulouse, France
D. Fabre
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse); Allée Camille Soula, F-31400 Toulouse, France
F. Giannetti
Affiliation:
DIIN, Universitá degli Studi di Salerno, Via Giovanni Paolo II, 84084 Fisciano (SA), Italy
P. Luchini
Affiliation:
DIIN, Universitá degli Studi di Salerno, Via Giovanni Paolo II, 84084 Fisciano (SA), Italy
*
†Email address for correspondence: vcitro@unisa.it
Get access Rights & Permissions [Opens in a new window]

Abstract

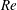We study the flow past a sphere rotating in the transverse direction with respect to the incoming uniform flow, and particularly consider the stability features of the wake as a function of the Reynolds number $Re$ and the sphere dimensionless rotation rate 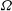$\unicode[STIX]{x1D6FA}$. Direct numerical simulations and three-dimensional global stability analyses are performed in the ranges 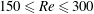$150\leqslant \mathit{Re}\leqslant 300$ and 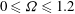$0\leqslant \unicode[STIX]{x1D6FA}\leqslant 1.2$. We first describe the base flow, computed as the steady solution of the Navier–Stokes equation, with special attention to the structure of the recirculating region and to the lift force exerted on the sphere. The stability analysis of this base flow shows the existence of two different unstable modes, which occur in different regions of the 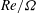$Re/\unicode[STIX]{x1D6FA}$ parameter plane. Mode I, which exists for weak rotations (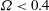$\unicode[STIX]{x1D6FA}<0.4$), is similar to the unsteady mode existing for a non-rotating sphere. Mode II, which exists for larger rotations (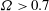$\unicode[STIX]{x1D6FA}>0.7$), is characterized by a larger frequency. Both modes preserve the planar symmetry of the base flow. We detail the structure of these eigenmodes, as well as their structural sensitivity, using adjoint methods. Considering small rotations, we then compare the numerical results with those obtained using weakly nonlinear approaches. We show that the steady bifurcation occurring for $Re>212$ for a non-rotating sphere is changed into an imperfect bifurcation, unveiling the existence of two other base-flow solutions which are always unstable.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Instability: Instability Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 807 , 25 November 2016 , pp. 62 - 86
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Brandt, L., Henningson, D. S., Hoepffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18, 068102.CrossRefGoogle Scholar
Bagheri, S., Åkervik, E., Brandt, L. & Henningson, D. S. 2009a Matrix-free methods for the stability and control of boundary layers. AIAA J. 47 (5), 1057–1068.Google Scholar
Bagheri, S., Schlatter, P., Schmid, P. J. & Henningson, D. S. 2009b Global stability of a jet in crossflow. J. Fluid Mech. 624, 33–44.Google Scholar
Citro, V., Giannetti, F., Luchini, P. & Auteri, F. 2015 Global stability and sensitivity analysis of boundary-layer flows past a hemispherical roughness element. Phys. Fluids 27, 084110.Google Scholar
Citro, V., Luchini, P., Giannetti, F. & Auteri, F. 2016 Efficient stabilization and acceleration of numerical simulation of fluid flows by residual recombination. J. Comput. Phys (submitted).Google Scholar
Constantinescu, G. S. & Squires, K. D.2000 LES and DNS investigation of turbulent flow over a sphere. AIAA Paper 0540.CrossRefGoogle Scholar
Doedel, E.1986, AUTO: software for continuation and bifurcation problems in ordinary differential equations. Tech. Rep. California Institute of Technology.Google Scholar
Fabre, D., Auguste, F. & Magnaudet, J. 2008 Bifurcations and symmetry breaking in the wake of axisymmetric bodies. Phys. Fluids 20 (5), 051702.CrossRefGoogle Scholar
Fabre, D., Tchoufag, J., Citro, V., Giannetti, F. & Luchini, P. 2016 The flow past a freely rotating sphere. Theor. Comput. Fluid Dyn. doi:10.1007/s00162-016-0405-x.Google Scholar
Fabre, D., Tchoufag, J. & Magnaudet, J. 2012 The steady oblique path of buoyancy-driven disks and spheres. J. Fluid Mech. 707, 24–36.CrossRefGoogle Scholar
Feldman, Y. & Gelfgat, A. Y. 2009 On pressure–velocity coupled time-integration of incompressible Navier–Stokes equations using direct inversion of Stokes operator or accelerated multigrid technique. Comput. Struct. 87, 710–720.Google Scholar
Fischer, P. 1997 An overlapping Schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133, 84–101.Google Scholar
Giacobello, M., Ooi, A. & Balachandar, S. 2009 Wake structure of a transversely rotating sphere at moderate Reynolds numbers. J. Fluid Mech. 621, 103–130.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Golubitsky, M. & Stewart, I. 2012 Singularities and Groups in Bifurcation Theory, vol. 2. Springer.Google Scholar
Ince, E. L. 1926 Ordinary Differential Equations. Dover.Google Scholar
Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19.Google Scholar
Kim, D. 2009 Laminar flow past a sphere rotating in the transverse direction. J. Mech. Sci. Technol. 23, 578–589.Google Scholar
Kim, D. & Choi, H. 2002 Laminar flow past a sphere rotating in the streamwise direction. J. Fluid Mech. 461, 365–386.Google Scholar
Kurose, R. & Komori, S. 1999 Drag and lift forces on a rotating sphere in a linear shear flow. J. Fluid Mech. 384, 183–206.Google Scholar
Kuznetsov, Y. A. & Levitin, V. V.1996 CONTENT, a multiplatform continuation environment. Tech. Rep. CWI.Google Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.Google Scholar
Luchini, P., Giannetti, F. & Pralits, J. 2007 An iterative algorithm for the numerical computation of bluff-body wake instability modes and its application to a freely vibrating cylinder. In BBVIV5, Fifth Conference on Bluff Body Wakes and Vortex-Induced Vibrations, Costa do Sauipe, Brazil, 12–15 Dec. (ed. Leweke, T., Meneghini, J. & Williamson, C.), pp. 129–132.Google Scholar
Magarvey, R. H. & Bishop, R. L. 1965 Vortices in sphere wakes. Can. J. Phys. 43, 1649–1656.Google Scholar
Meliga, P., Chomaz, J. M. & Sipp, D. 2009a Global mode interaction and pattern selection in the wake of a disk: a weakly nonlinear expansion. J. Fluid Mech. 633, 159–189.CrossRefGoogle Scholar
Meliga, P., Chomaz, J.-M. & Sipp, D. 2009b Unsteadiness in the wake of disks and spheres: instability, receptivity and control using direct and adjoint global stability analyses. J. Fluid Struct. 25, 601–616.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.Google Scholar
Nakamura, I. 1976 Steady wake behind a sphere. Phys. Fluids 19, 5.CrossRefGoogle Scholar
Natarajan, R. & Acrivos, A. 1993 The instability of the steady flow past spheres and disks. J. Fluid Mech. 254, 323–344.Google Scholar
Niazmand, H. & Renksizbukut, M. 2003 Surface effects on transient three-dimensional flows around rotating spheres at moderate Reynolds numbers. Comput. Fluids 32, 1405–1433.Google Scholar
Pier, B. 2013 Periodic and quasiperiodic vortex shedding in the wake of a rotating sphere. J. Fluid Struct. 41, 43–50.Google Scholar
Poon, E. K. W., Ooi, A. S. H., Giacobello, M. & Cohen, R. C. Z. 2010 Laminar flow structures from a rotating sphere: effect of rotating axis angle. Intl J. Heat Fluid Flow 31, 961–972.Google Scholar
Poon, E. K. W., Ooi, A. S. H., Giacobello, M., Iaccarino, G. & Chung, D. 2014 Flow past a transversely rotating sphere at Reynolds numbers above the laminar regime. J. Fluid Mech. 759, 751–781.CrossRefGoogle Scholar
Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.Google Scholar
Saad, Y. 2003 Iterative Methods for Sparse Linear Systems. SIAM.Google Scholar
Schlatter, P., Bagheri, S. & Henningson, D. S. 2011 Self-sustained global oscillations in a jet in crossflow. Theor. Comput. Fluid Dyn. 25, 129–146.Google Scholar
Shroff, G. M. & Keller, H. B. 1993 Stabilization of unstable procedures: the recursive projection method. SIAM J. Numer. Anal. 30, 1099–1120.CrossRefGoogle Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean-flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.Google Scholar
Tammisola, O., Giannetti, F., Citro, V. & Juniper, M. P. 2014 Second-order perturbation of global modes and implications for spanwise wavy actuation. J. Fluid Mech. 755, 314–335.Google Scholar
Tannehill, J. C., Anderson, D. A. & Pletcher, R. H. 1997 Computational Fluid Mechanics and Heat Transfer. Taylor & Francis.Google Scholar
Tchoufag, J., Assemat, P., Fabre, D. & Meliga, P. 2011 Stabilité globale linéaire et faiblement non-linéaire du sillage d’objets axisymétriques. In 20ème Congrès Français de Mécanique, 28 août/2 Sept. 2011, 25044 Besançon, France.Google Scholar
Tchoufag, J., Fabre, D. & Magnaudet, J. 2013 Linear stability and sensitivity of the flow past a fixed ellipsoidal bubble. Phys. Fluids 054108.Google Scholar
Tchoufag, J., Fabre, D. & Magnaudet, J. 2014a Global linear stability analysis of the wake and path of buoyancy-driven disks and thin cylinders. J. Fluid Mech. 740, 278–311.Google Scholar
Tchoufag, J., Fabre, D. & Magnaudet, J. 2014b Weakly nonlinear model with exact coefficients for the fluttering and spiraling motion of buoyancy-driven bodies. Phys. Rev. Lett. 115, 11.Google Scholar
Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.Google Scholar
Trottenberg, U., Oosterlee, C. W. & Schüller, A. 2001 Multigrid. Academic.Google Scholar
Tufo, H. M. & Fischer, P. F. 1999 Terascale spectral element algorithms and implementations. In Proceedings of the 1999 ACM/IEEE Conference on Supercomputing. ACM.Google Scholar
Vanka, S. P. 1986 Block-implicit multigrid solution of Navier–Stokes equations in primitive variables. J. Comput. Phys. 65, 138–158.CrossRefGoogle Scholar