1. Introduction
The coexistence of shear, rotation and stratification is ubiquitous in geophysical and astrophysical fluid flows (e.g. Balbus & Hawley Reference Balbus and Hawley1998; Vallis Reference Vallis2006; Smyth & Carpenter Reference Smyth and Carpenter2019) and so a considerable effort has been expended to understand the flows generated. A well-established starting point is to assess the stability of a simple base flow commensurate with the physics and boundary conditions present to learn about the various instability mechanisms. Instabilities due to the presence of shear have a very classical history (e.g. Schmid & Henningson Reference Schmid and Henningson2001; Drazin & Reid Reference Drazin and Reid2004) as does the presence of shear and rotation which has been studied for over a century (e.g. Rayleigh Reference Rayleigh1917; Drazin Reference Drazin2002, chapter 3). It is now well known that rotation introduces the possibility of centrifugal (CF) instability with the most unstable CF mode generally assumed to be streamwise independent (or axisymmetric in a cylindrical geometry), and that Rayleigh's criterion provides a sufficient condition for stability. Adding stable stratification to shear was long thought to simply stabilise the flow but in some cases it can cause destabilisation through a resonance mechanism between either a pair of internal gravity waves (IGWs, which are waves supported by stratification), or an IGW and a Tollmien–Schlichting wave (TSW, which are waves supported by shear) (Facchini et al. Reference Facchini, Favier, Le Gal, Wang and Le Bars2018; Le Gal et al. Reference Le Gal, Harlander, Borcia, Le Dizès, Chen and Favier2021).
A combination of stable stratification and rotation with shear can destabilise the flow further, and when both physical effects are necessary to trigger instability, it is referred to as strato-rotational instability (SRI). Although this was first studied by Kushner, McIntyre & Shepherd (Reference Kushner, McIntyre and Shepherd1998) for planar geometry and Molemaker, McWilliams & Yavneh (Reference Molemaker, McWilliams and Yavneh2001) and Yavneh, McWilliams & Molemaker (Reference Yavneh, McWilliams and Molemaker2001) for cylindrical geometry, the name SRI was introduced by Dubrulle et al. (Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005). Wentzel–Kramers–Brillouin (WKB) analysis reveals SRI to be associated with a resonance between Kelvin waves (KWs, which are waves supported by rotation), IGWs or a mixture of both, trapped at either side of the domain (Kushner et al. Reference Kushner, McIntyre and Shepherd1998; Yavneh et al. Reference Yavneh, McWilliams and Molemaker2001; Dubrulle et al. Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005; Vanneste & Yavneh Reference Vanneste and Yavneh2007; Park, Billant & Baik Reference Park, Billant and Baik2017; Wang & Balmforth Reference Wang and Balmforth2018, see also table 1), which leads to some diagnostic tools for this instability: the eigenfunctions will be localised at either side of the channel, there will be very thin ranges of unstable vertical wavenumbers for each fixed horizontal wavenumber, and there will be crossings of frequency branches that cause the positive growth rate. Both Yavneh et al. (Reference Yavneh, McWilliams and Molemaker2001) and Dubrulle et al. (Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005) show example eigenfunctions of resonance and global modes, although the latter may be explained by the discussion of stratification-modified CF instability below. SRI is streamwise dependent and persists beyond the Rayleigh line (Yavneh et al. Reference Yavneh, McWilliams and Molemaker2001), so there are multiple ways to identify an instability as SRI. This instability has received much attention in recent years, with many further numerical and experimental studies to complement the WKB analysis (Shalybkov & Rüdiger Reference Shalybkov and Rüdiger2005; Le Bars & Le Gal Reference Le Bars and Le Gal2007; Park & Billant Reference Park and Billant2013; Ibanez, Swinney & Rodenborn Reference Ibanez, Swinney and Rodenborn2016; Leclercq, Nguyen & Kerswell Reference Leclercq, Nguyen and Kerswell2016; Park et al. Reference Park, Billant, Baik and Seo2018; Robins, Kersalé & Jones Reference Robins, Kersalé and Jones2020; Lopez, Lopez & Marques Reference Lopez, Lopez and Marques2023). A further instability, named the radiative instability (RI), was identified in Taylor–Couette flow (TCF) by Le Dizès & Riedinger (Reference Le Dizès and Riedinger2010), which built on other studies of RI for stratified vortices (Billant & Le Dizès Reference Billant and Le Dizès2009; Le Dizès & Billant Reference Le Dizès and Billant2009) (and further developed through experiments in Riedinger, Le Dizès & Meunier Reference Riedinger, Le Dizès and Meunier2011). This instability takes the form of a mode localised or ‘trapped’ on one side, and is unstable for a continuous band of wavenumbers (Le Dizès & Riedinger Reference Le Dizès and Riedinger2010). SRI and RI can be shown to be related by removing the outer boundary (Le Dizès & Riedinger Reference Le Dizès and Riedinger2010).
Table 1. Key references in the SRI literature.

Despite all this work, it is still unknown exactly how the stability of CF modes will change due to stratification. A theme in the literature is that the streamwise-independent modes of CF instability are the most unstable for rotating shear flows, and so Rayleigh's criterion provides information about the general stability of the flow. The label ‘centrifugal instability’ has therefore become associated with streamwise-independent modes. However, there is a large branch of CF modes in wavenumber space which includes streamwise-dependent perturbations (although these are seen to be only ‘weakly’ streamwise dependent when compared with the resonance-type SRI, see Park et al. Reference Park, Billant and Baik2017, Reference Park, Billant, Baik and Seo2018). If stratification increases the growth rate of these three-dimensional (3-D) modes, then it would be possible to find CF instability beyond the Rayleigh line. By the definition of SRI given by Dubrulle et al. (Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005), this would be considered SRI, as it requires both rotation and stratification to be unstable. However, as it is does not become unstable as a consequence of two waves interacting, it is different from the resonance instability which is commonly associated with SRI. To avoid confusion, here we label instabilities that require both rotation and stratification to be present as either resonance-type SRI, or stratification-modified CF instability. It is unclear from the literature whether streamwise-dependent instabilities that persist beyond the Rayleigh line can be of CF origin. Leclercq et al. (Reference Leclercq, Nguyen and Kerswell2016) provide a first insight into this but find that CF and SRI are often difficult to distinguish at low Reynolds numbers.
The current paper aims to develop our understanding of this for a stratified, rotating shear flow in a channel geometry where the shear is driven by a combination of wall movement and applied pressure gradient, i.e. we take a mixed plane Couette–Poiseuille flow (CPF) profile. The reasons for this are threefold. First, this set-up allows us to examine how a TSW shear instability interacts with the CF instability and Rayleigh's criterion even in the absence of stratification. A key question is do they operate independently of each other or is there some interaction to produce instability in new parts of parameter space? In addition, it is possible to assess their relevant strengths (growth rates) in parts of parameter space where they coexist. Secondly, a non-constant shear introduces a barotropic critical layer into the stability problem whose effect is unknown. Wang & Balmforth (Reference Wang and Balmforth2018) found a new type of SRI instability by carefully examining the baroclinic critical layer but were unable to carry out a similar study on the barotropic critical layer as it was absent for their chosen constant shear background state. To pursue this, we wanted to find regions in this extended parameter space where SRI dominates CF. Third, the set-up allows us to explore the effect of a more complicated shear profile on the possibility of fully localising CF instabilities away from boundaries, which has obvious implications for astrophysical applications. Beyond the more complicated basic shear chosen, however, the main thrust of this work is examining the effect of stratification on the CF instability. In particular, we identify instability in stratified, rotating CPF beyond the Rayleigh line, which appears to be more similar to CF instability than the resonance-type SRI.
The formulated problem builds on a number of areas of the literature, and ties some previous studies together. The linear stability of unstratified CPF was initially studied asymptotically by Potter (Reference Potter1966), who identified how much pressure gradient needs to be added to plane Couette flow (PCF) to see TSW instability (e.g. Drazin Reference Drazin2002, chapter 8). Many studies built upon this, confirming the critical value and probing other aspects such as the shape of the neutral curve and the finite-amplitude states generated (Hains Reference Hains1967; Reynolds & Potter Reference Reynolds and Potter1967; Cowley & Smith Reference Cowley and Smith1985; Balakumar Reference Balakumar1997). Motivated by astrophysical applications, rotation was only recently added to this flow by Ghosh & Mukhopadhyay (Reference Ghosh and Mukhopadhyay2021) but they do not systematically examine changing the rotation rate. We do this and also introduce stratification. This study of the CPF profile also of course extends some of the rotating and stratified PCF studies discussed above, many of which focus on SRI, and studying this flow also paves the way to examine the effect of the barotropic critical layer on resonance instabilities. Adding rotation to stratified CPF also builds on the experimental and numerical studies of both Facchini et al. (Reference Facchini, Favier, Le Gal, Wang and Le Bars2018) and Le Gal et al. (Reference Le Gal, Harlander, Borcia, Le Dizès, Chen and Favier2021), who find resonance instabilities in non-rotating PCF and plane Poiseuille flow (PPF). Leclercq et al. (Reference Leclercq, Nguyen and Kerswell2016), Park et al. (Reference Park, Billant and Baik2017) and Park et al. (Reference Park, Billant, Baik and Seo2018) study TCF in regions of parameter space where SRI and CF instabilities can coexist. The first of these looks in particular at how the two are connected at finite Reynolds number, whereas the other two investigate which instability is stronger and how to distinguish them. Some of the work presented here builds on parts of those studies by providing a planar geometry counterpart and extending beyond the Rayleigh unstable region.
The model and equations are introduced in § 2, along with details of the numerical methods. This is followed by two sections presenting numerical results. The first presents a parameter search over the unstratified but rotating CPF problem in order to identify the instability that first causes destabilisation in each region of parameter space. The second then examines the effect of introducing stable stratification to rotating CPF. Here the focus is to probe the persistence of CF type modes beyond the Rayleigh line, and the existence of resonance instabilities in CPF, while also looking at how the instabilities change as we move through the possible CPF base flow profiles. We conclude in § 5 with a discussion of the results and options for further study.
2. Problem formulation and preliminaries
2.1. Base flow and governing equations
We consider a fluid flow driven by both a moving wall and a pressure gradient in a channel of width ![]() $L$ and characteristic speed
$L$ and characteristic speed ![]() $V$ (defined in the following). The flow is made non-dimensional through length, time, velocity, pressure and density scales
$V$ (defined in the following). The flow is made non-dimensional through length, time, velocity, pressure and density scales ![]() $L$,
$L$, ![]() $L/V$,
$L/V$, ![]() $V$,
$V$, ![]() $\rho _0 V^2$ and
$\rho _0 V^2$ and ![]() $\rho _0 V^2/gL$, respectively, where
$\rho _0 V^2/gL$, respectively, where ![]() $\rho _0$ is a representative density of the background field
$\rho _0$ is a representative density of the background field ![]() $\rho _B(z)$ and
$\rho _B(z)$ and ![]() $g$ the acceleration due to gravity. The direction of driving is along the
$g$ the acceleration due to gravity. The direction of driving is along the ![]() $x$-axis, the channel walls are located at
$x$-axis, the channel walls are located at ![]() $y=0$ and
$y=0$ and ![]() $1$, and
$1$, and ![]() $z$ is the spanwise direction anti-aligned with gravity. The system rotates at constant rate
$z$ is the spanwise direction anti-aligned with gravity. The system rotates at constant rate ![]() $\varOmega$ around the
$\varOmega$ around the ![]() $z$-axis, and the density varies with
$z$-axis, and the density varies with ![]() $z$ under the Boussinesq approximation: see figure 1. The dimensionless buoyancy frequency,
$z$ under the Boussinesq approximation: see figure 1. The dimensionless buoyancy frequency, ![]() $N=\sqrt {- \mathrm {d}\rho _B/ \mathrm {d}z}$ is assumed to be real, positive and constant, so that the stratification is stable. The speed
$N=\sqrt {- \mathrm {d}\rho _B/ \mathrm {d}z}$ is assumed to be real, positive and constant, so that the stratification is stable. The speed ![]() $V$ is chosen such that the base flow within the channel is
$V$ is chosen such that the base flow within the channel is
where ![]() $0\leq \varGamma \leq 1$ is the parameter which sets the relative size of the PCF and PPF components or, equivalently,
$0\leq \varGamma \leq 1$ is the parameter which sets the relative size of the PCF and PPF components or, equivalently, ![]() $\varGamma$ is the top (non-dimensionalised) wall speed and
$\varGamma$ is the top (non-dimensionalised) wall speed and ![]() $-({2}/{Re})(1-\varGamma )$ the imposed (non-dimensionalised) pressure gradient. The total velocity is written as
$-({2}/{Re})(1-\varGamma )$ the imposed (non-dimensionalised) pressure gradient. The total velocity is written as ![]() $\boldsymbol {u}_T=\boldsymbol {U}_B + \boldsymbol {u}=\boldsymbol {U}_B+u{\boldsymbol {\hat {x}}}+v{\boldsymbol {\hat {y}}}+w{\boldsymbol {\hat {z}}}$, the total pressure as
$\boldsymbol {u}_T=\boldsymbol {U}_B + \boldsymbol {u}=\boldsymbol {U}_B+u{\boldsymbol {\hat {x}}}+v{\boldsymbol {\hat {y}}}+w{\boldsymbol {\hat {z}}}$, the total pressure as ![]() $P_T=P_B+p$ and the total density field as
$P_T=P_B+p$ and the total density field as ![]() $\rho _T=\rho _B + \rho$. The dimensionless parameters that determine the flow, along with
$\rho _T=\rho _B + \rho$. The dimensionless parameters that determine the flow, along with ![]() $\varGamma$,
$\varGamma$, ![]() $\varOmega$ and
$\varOmega$ and ![]() $N$, are the Reynolds number
$N$, are the Reynolds number ![]() ${{Re}}=LV/\nu$ and the Prandtl number
${{Re}}=LV/\nu$ and the Prandtl number ![]() ${ {Pr}}=\nu /\kappa$, where
${ {Pr}}=\nu /\kappa$, where ![]() $\nu$ and
$\nu$ and ![]() $\kappa$ are the kinematic viscosity and coefficient of diffusion.
$\kappa$ are the kinematic viscosity and coefficient of diffusion.

Figure 1. The plane Couette–Poiseuille (non-dimensional) set-up. The base flow is in the ![]() ${\boldsymbol {\hat {x}}}$ direction with the walls at
${\boldsymbol {\hat {x}}}$ direction with the walls at ![]() $y=0$ at rest and
$y=0$ at rest and ![]() $y=1$ moving at
$y=1$ moving at ![]() $\varGamma$. Stratification and rotation are aligned with the
$\varGamma$. Stratification and rotation are aligned with the ![]() $z$-axis. The dashed blue line shows the base flow for
$z$-axis. The dashed blue line shows the base flow for ![]() $\varGamma =3/8$, with the dotted blue lines showing the PCF and PPF components.
$\varGamma =3/8$, with the dotted blue lines showing the PCF and PPF components.
Small perturbations are governed by linearised Boussinesq equations
The CF buoyancy term is not retained here in keeping with previous work (e.g. Yavneh et al. Reference Yavneh, McWilliams and Molemaker2001; Dubrulle et al. Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005; Park et al. Reference Park, Billant and Baik2017; Wang & Balmforth Reference Wang and Balmforth2018) as stratification (when present) is presumed to dominate rotation, i.e. ![]() $N^2/\varOmega ^2$ is large. However, retaining this (as advocated by Lopez, Marques & Avila Reference Lopez, Marques and Avila2013) to test this approximation would be an interesting further study.
$N^2/\varOmega ^2$ is large. However, retaining this (as advocated by Lopez, Marques & Avila Reference Lopez, Marques and Avila2013) to test this approximation would be an interesting further study.
The flow satisfies the no-slip conditions on the channel walls, leading to vanishing boundary conditions on the velocity perturbations. The boundary condition for the density perturbation is that the normal derivative vanishes, which corresponds to no flux of density through the surface into or out of the domain:
2.2. Normal modes
Writing the velocity, pressure and density perturbations in normal mode form,
and writing out the governing equations in component form gives
where ![]() $\mathrm {D}=\mathrm {d}/\mathrm {d} y$ (also
$\mathrm {D}=\mathrm {d}/\mathrm {d} y$ (also ![]() $U_B':=DU_B$). The non-dimensional horizontal and vertical wavenumbers
$U_B':=DU_B$). The non-dimensional horizontal and vertical wavenumbers ![]() $k_x$ and
$k_x$ and ![]() $k_z$ are both real numbers. The growth rate is given by the real part of
$k_z$ are both real numbers. The growth rate is given by the real part of ![]() $\sigma$, so that a positive value corresponds to an unstable mode. The boundary conditions become
$\sigma$, so that a positive value corresponds to an unstable mode. The boundary conditions become
2.3. Numerical methods
Equations (2.7)–(2.12) are an eigenvalue problem for eigenvalue ![]() $\sigma$ and associated eigenfunction
$\sigma$ and associated eigenfunction ![]() $(\hat {u},\hat {v},\hat {w},\hat {p},\hat {\rho })$. Once the parameters
$(\hat {u},\hat {v},\hat {w},\hat {p},\hat {\rho })$. Once the parameters ![]() $\varGamma$,
$\varGamma$, ![]() $\varOmega$,
$\varOmega$, ![]() $N$,
$N$, ![]() ${ {Re}}$,
${ {Re}}$, ![]() ${ {Pr}}$,
${ {Pr}}$, ![]() $k_x$ and
$k_x$ and ![]() $k_z$ are chosen, a spectral collocation method is used to solve the problem. Combinations of the Chebyshev polynomials are used as the basic functions to implicitly satisfy the boundary conditions (e.g. Boyd Reference Boyd2000). In § 3, the critical Reynolds number (
$k_z$ are chosen, a spectral collocation method is used to solve the problem. Combinations of the Chebyshev polynomials are used as the basic functions to implicitly satisfy the boundary conditions (e.g. Boyd Reference Boyd2000). In § 3, the critical Reynolds number (![]() ${ {Re}}_c$) is found at points in
${ {Re}}_c$) is found at points in ![]() $\varGamma$–
$\varGamma$–![]() $\varOmega$ space. To find
$\varOmega$ space. To find ![]() ${ {Re}}_c$ at a specific pair
${ {Re}}_c$ at a specific pair ![]() $(\varGamma,\varOmega )$, each
$(\varGamma,\varOmega )$, each ![]() ${ {Re}}$ must be tested and the largest growth rate over a selected range of
${ {Re}}$ must be tested and the largest growth rate over a selected range of ![]() $k_x$ and
$k_x$ and ![]() $k_z$ has to be found. The critical Reynolds number is the largest Reynolds number where the largest growth rate is not positive (i.e. the largest Reynolds number where every wavenumber pair is stable). To characterise the instability at the lowest possible
$k_z$ has to be found. The critical Reynolds number is the largest Reynolds number where the largest growth rate is not positive (i.e. the largest Reynolds number where every wavenumber pair is stable). To characterise the instability at the lowest possible ![]() ${ {Re}}$, the angle
${ {Re}}$, the angle ![]() $\theta =\tan ^{-1}(k_z/k_x)$ was recorded (by symmetries of the problem it is sufficient to just look over
$\theta =\tan ^{-1}(k_z/k_x)$ was recorded (by symmetries of the problem it is sufficient to just look over ![]() $k_x,k_z\geq 0$ so
$k_x,k_z\geq 0$ so ![]() $0 \leq \theta \leq 90^{\circ }$). The maximum Reynolds number used was
$0 \leq \theta \leq 90^{\circ }$). The maximum Reynolds number used was ![]() $10^6$ so if the point in parameter space is still stable at this
$10^6$ so if the point in parameter space is still stable at this ![]() ${ {Re}}$ value (i.e. critical Reynolds number is greater than or equal to this value), then we labelled the point in
${ {Re}}$ value (i.e. critical Reynolds number is greater than or equal to this value), then we labelled the point in ![]() $\varGamma$–
$\varGamma$–![]() $\varOmega$ space as ‘stable’. The spectral resolution used depended on the Reynolds number, varying between
$\varOmega$ space as ‘stable’. The spectral resolution used depended on the Reynolds number, varying between ![]() $50$ and
$50$ and ![]() $200$ Chebyshev modes to express each field
$200$ Chebyshev modes to express each field ![]() $(\hat {u},\hat {v},\hat {w},\hat {p},\hat {\rho })$. The results were checked at higher spectral resolution (up to
$(\hat {u},\hat {v},\hat {w},\hat {p},\hat {\rho })$. The results were checked at higher spectral resolution (up to ![]() $250$ where needed), ensuring the most unstable modes were resolved well. All results matched to at least three but mostly four significant figures and eigenfunctions are normalised so that
$250$ where needed), ensuring the most unstable modes were resolved well. All results matched to at least three but mostly four significant figures and eigenfunctions are normalised so that ![]() $\max \hat {u}=1$. The code was checked using the points marked in figure 2, e.g. the critical Reynolds numbers of Orszag (Reference Orszag1971) and Lezius & Johnston (Reference Lezius and Johnston1976). When stratification is introduced in § 4, the code was checked by reproducing figures from Facchini et al. (Reference Facchini, Favier, Le Gal, Wang and Le Bars2018).
$\max \hat {u}=1$. The code was checked using the points marked in figure 2, e.g. the critical Reynolds numbers of Orszag (Reference Orszag1971) and Lezius & Johnston (Reference Lezius and Johnston1976). When stratification is introduced in § 4, the code was checked by reproducing figures from Facchini et al. (Reference Facchini, Favier, Le Gal, Wang and Le Bars2018).

Figure 2. Stability of rotating CPF. The grey shading shows where Rayleigh's criterion for inviscid, linear stability of streamwise-independent perturbations is violated (the white regions are predicted to be stable). The dots correspond to unstable modes found in the literature, with black, purple and red corresponding to Orszag (Reference Orszag1971), Lezius & Johnston (Reference Lezius and Johnston1976) and Ghosh & Mukhopadhyay (Reference Ghosh and Mukhopadhyay2021), respectively. The orange and blue lines running horizontally show unstable and stable points, respectively, known from the CPF literature (e.g. Potter Reference Potter1966; Hains Reference Hains1967). The vertical pink line at ![]() $\varGamma =1$ indicates the known instability due to a connection between PCF and Rayleigh–Bénard convection, whereas the vertical cyan line at
$\varGamma =1$ indicates the known instability due to a connection between PCF and Rayleigh–Bénard convection, whereas the vertical cyan line at ![]() $\varGamma =0$ represents instability known from Lezius & Johnston (Reference Lezius and Johnston1976). The green ‘+’ symbols show a selection of points from Ghosh & Mukhopadhyay (Reference Ghosh and Mukhopadhyay2021) that are found to be stable for certain Reynolds numbers and wavenumber pairs. This plot demonstrates that the shown results from the literature do tend to obey Rayleigh's criterion, although they are completely focused on anticyclonic rotation. The plot also shows that PPF is much more susceptible to CF than PCF, due to symmetry.
$\varGamma =0$ represents instability known from Lezius & Johnston (Reference Lezius and Johnston1976). The green ‘+’ symbols show a selection of points from Ghosh & Mukhopadhyay (Reference Ghosh and Mukhopadhyay2021) that are found to be stable for certain Reynolds numbers and wavenumber pairs. This plot demonstrates that the shown results from the literature do tend to obey Rayleigh's criterion, although they are completely focused on anticyclonic rotation. The plot also shows that PPF is much more susceptible to CF than PCF, due to symmetry.
2.4. Rayleigh's criterion for CPF
Rayleigh's criterion is a necessary condition for streamwise-independent instability in rotating inviscid fluids (Rayleigh Reference Rayleigh1917; Greenspan Reference Greenspan1990, chapter 6) and, therefore, should capture the behaviour of the flow for large Reynolds number. For inviscid rotating PCF, the criterion reduces to ‘the flow is stable provided ![]() $\varOmega \leq 0$ or
$\varOmega \leq 0$ or ![]() $\varOmega \geq 1/2$’. A stronger ‘if and only if’ condition can be found directly from the exact analytical solutions of the stability problem due to its simplicity for PCF. This is presented in Appendix A where it is shown to be also valid for a stratified fluid.
$\varOmega \geq 1/2$’. A stronger ‘if and only if’ condition can be found directly from the exact analytical solutions of the stability problem due to its simplicity for PCF. This is presented in Appendix A where it is shown to be also valid for a stratified fluid.
Rayleigh's criterion is derived for CPF in Appendix B, which gives a region of parameter space shown in figure 2 that is guaranteed to be stable to streamwise-independent perturbations in the inviscid limit. A continuous connection is expected between the stability boundaries for PPF (which is independent of the direction of rotation), and those for PCF, but this connection is certainly non-trivial. This criterion is shown to apply to both stratified and unstratified fluids in Appendix B.
Despite this condition being derived assuming streamwise-independent perturbations, empirical evidence suggests that these perturbations are the most unstable, and so this criterion does, in fact, determine the stability of the flow more generally. For example, this assumption has been made by Lezius & Johnston (Reference Lezius and Johnston1976) in studying both viscous PPF and viscous PCF, who cite the experimental work of Hart (Reference Hart1971) as well as mathematical analogy with the proof by Joseph (Reference Joseph1966) for a Couette flow profile heated from below. This, however, is not the case when other instabilities are present in the flow, such as the TSW instability, so we can expect Rayleigh's criterion to fail in governing the general stability when the base flow is close to PPF.
3. Numerical results I: instabilities in unstratified rotating CPF
Before treating the stratified problem, we first investigate the stability of unstratified rotating CPF, which corresponds to setting ![]() ${ {Pr}}=\infty$,
${ {Pr}}=\infty$, ![]() $N=0$ and
$N=0$ and ![]() $\hat \rho = 0$ in (2.7)–(2.12). This simplification removes resonance instabilities (either those of SRI, or those in non-rotating but stratified flows, e.g. Yavneh et al. Reference Yavneh, McWilliams and Molemaker2001; Vanneste & Yavneh Reference Vanneste and Yavneh2007; Facchini et al. Reference Facchini, Favier, Le Gal, Wang and Le Bars2018; Le Gal et al. Reference Le Gal, Harlander, Borcia, Le Dizès, Chen and Favier2021), meaning the resolution required for the wavenumber grid is not as fine as that required with stratification present. The unstratified case also provides a useful reference point when the stratified problem is studied later, aiding in the identification of instabilities. Although Ghosh & Mukhopadhyay (Reference Ghosh and Mukhopadhyay2021) did introduce rotation into CPF, the work of this section increases the breadth of study over different rotation rates and shear profiles, bridging the gap between the literature of rotating PCF and rotating PPF.
$\hat \rho = 0$ in (2.7)–(2.12). This simplification removes resonance instabilities (either those of SRI, or those in non-rotating but stratified flows, e.g. Yavneh et al. Reference Yavneh, McWilliams and Molemaker2001; Vanneste & Yavneh Reference Vanneste and Yavneh2007; Facchini et al. Reference Facchini, Favier, Le Gal, Wang and Le Bars2018; Le Gal et al. Reference Le Gal, Harlander, Borcia, Le Dizès, Chen and Favier2021), meaning the resolution required for the wavenumber grid is not as fine as that required with stratification present. The unstratified case also provides a useful reference point when the stratified problem is studied later, aiding in the identification of instabilities. Although Ghosh & Mukhopadhyay (Reference Ghosh and Mukhopadhyay2021) did introduce rotation into CPF, the work of this section increases the breadth of study over different rotation rates and shear profiles, bridging the gap between the literature of rotating PCF and rotating PPF.
3.1. Critical  ${ {Re}}$ and growth rates
${ {Re}}$ and growth rates
Figure 3 displays a contour plot of the critical Reynolds number (defined in § 2.3), ![]() ${ {Re}}_c$, in
${ {Re}}_c$, in ![]() $\varGamma$–
$\varGamma$–![]() $\varOmega$ space, using a log scale. This plot shows good agreement with Rayleigh's criterion, presented in figure 2 for
$\varOmega$ space, using a log scale. This plot shows good agreement with Rayleigh's criterion, presented in figure 2 for ![]() $\varGamma \gtrsim 0.15$. (a thick red line indicates the boundary between stable and unstable regions). For
$\varGamma \gtrsim 0.15$. (a thick red line indicates the boundary between stable and unstable regions). For ![]() $\varGamma \lesssim 0.15$, there is, however, an extra small instability region, around
$\varGamma \lesssim 0.15$, there is, however, an extra small instability region, around ![]() $\varGamma =0.15$ and
$\varGamma =0.15$ and ![]() $\varOmega =0.5$ and then the strip of Tollmien–Schlichting shear instability for all
$\varOmega =0.5$ and then the strip of Tollmien–Schlichting shear instability for all ![]() $\varOmega$. The shading clearly shows that inside the region defined in Rayleigh's criterion, the value of
$\varOmega$. The shading clearly shows that inside the region defined in Rayleigh's criterion, the value of ![]() ${ {Re}}_c$ drops significantly. This is explained by the competition between two types of modes, as discussed in the following.
${ {Re}}_c$ drops significantly. This is explained by the competition between two types of modes, as discussed in the following.

Figure 3. Contour plot of the critical Reynolds number, defined in § 2.3, over a range of ![]() $\varGamma$ and
$\varGamma$ and ![]() $\varOmega$. The solid red line shows the interface between the regions which are labelled as stable (i.e. the critical Reynolds number is found to be at least the maximum tested value of
$\varOmega$. The solid red line shows the interface between the regions which are labelled as stable (i.e. the critical Reynolds number is found to be at least the maximum tested value of ![]() $10^{6}$), and those which are found to be unstable. The plot not only clearly identifies the unstable regions, but also shows where the critical Reynolds number reaches its minimum.
$10^{6}$), and those which are found to be unstable. The plot not only clearly identifies the unstable regions, but also shows where the critical Reynolds number reaches its minimum.
Despite Rayleigh's criterion applying only to streamwise-independent (![]() $k_x=0$) perturbations, it is valid unless
$k_x=0$) perturbations, it is valid unless ![]() $\varGamma \lesssim 0.15$. This is consistent with the literature, where the general stability properties of rotating PCF (
$\varGamma \lesssim 0.15$. This is consistent with the literature, where the general stability properties of rotating PCF (![]() $\varGamma =1$ here) are thought to be governed by Rayleigh's criterion.
$\varGamma =1$ here) are thought to be governed by Rayleigh's criterion.
To investigate the possible types of instabilities for each point in the space of parameters ![]() $\varGamma$ and
$\varGamma$ and ![]() $\varOmega$, the orientation
$\varOmega$, the orientation ![]() $\theta$ of the first instability (defined in § 2.3) is shown in figure 4. The solid red line corresponds to the same line in figure 3. The points are separated into three types:
$\theta$ of the first instability (defined in § 2.3) is shown in figure 4. The solid red line corresponds to the same line in figure 3. The points are separated into three types: ![]() $\theta =0^\circ$ (
$\theta =0^\circ$ (![]() $k_z=0$) modes plotted in purple,
$k_z=0$) modes plotted in purple, ![]() $\theta =90^\circ$ (
$\theta =90^\circ$ (![]() $k_x=0$) modes plotted in green and
$k_x=0$) modes plotted in green and ![]() $0^\circ <\theta <90^\circ$ (3-D modes) plotted in orange.
$0^\circ <\theta <90^\circ$ (3-D modes) plotted in orange.

Figure 4. Orientation of the mode which first becomes unstable as Reynolds number is increased in rotating CPF. The purple regions have ![]() $\theta =0^\circ$ (
$\theta =0^\circ$ (![]() $k_z=0$, which are TSW), the green regions have
$k_z=0$, which are TSW), the green regions have ![]() $\theta =90^\circ$ (
$\theta =90^\circ$ (![]() $k_x=0$, which are CF modes), whereas the orange regions are first made unstable by a 3-D mode, with
$k_x=0$, which are CF modes), whereas the orange regions are first made unstable by a 3-D mode, with ![]() $0^\circ <\theta <90^\circ$. The white regions are those corresponding to the stable regions identified in figure 3 and are separated from the unstable regions by the red line. The dashed line shows the domain for the plot in figure 5. The solid black line shows the path in parameter space traced out by figures 7 and 8, whereas the black square shows the point used for the transition in figure 10, along with the eigenfunction shown in figure 11(a). The black diamonds correspond to locations of eigenfunctions that are displayed in subsequent plots. The plot clearly demonstrates that CF modes become unstable at lower Reynolds numbers than Tollmien–Schlichting modes, even in regions where they coexist. These instabilities are completely separate processes which are each two-dimensional in a way that is orthogonal to each other. Where the instabilities move into a new part of the parameter space, this separation is not observed and 3-D modes become unstable first.
$0^\circ <\theta <90^\circ$. The white regions are those corresponding to the stable regions identified in figure 3 and are separated from the unstable regions by the red line. The dashed line shows the domain for the plot in figure 5. The solid black line shows the path in parameter space traced out by figures 7 and 8, whereas the black square shows the point used for the transition in figure 10, along with the eigenfunction shown in figure 11(a). The black diamonds correspond to locations of eigenfunctions that are displayed in subsequent plots. The plot clearly demonstrates that CF modes become unstable at lower Reynolds numbers than Tollmien–Schlichting modes, even in regions where they coexist. These instabilities are completely separate processes which are each two-dimensional in a way that is orthogonal to each other. Where the instabilities move into a new part of the parameter space, this separation is not observed and 3-D modes become unstable first.

Figure 5. Plot of the growth rate, ![]() $\mathrm {Re}(\sigma )$, against the rotation rate,
$\mathrm {Re}(\sigma )$, against the rotation rate, ![]() $\varOmega$. For this plot,
$\varOmega$. For this plot, ![]() $\varGamma =0.1$ and
$\varGamma =0.1$ and ![]() ${ {Re}}=200\,000$. The wavenumbers of the three modes are given in the figure, and they correspond to a 2-D Tollmien–Schlichting mode, a 2-D CF mode and a 3-D mode. The wavenumbers were chosen as they are each the mode that first destabilises the flow at some
${ {Re}}=200\,000$. The wavenumbers of the three modes are given in the figure, and they correspond to a 2-D Tollmien–Schlichting mode, a 2-D CF mode and a 3-D mode. The wavenumbers were chosen as they are each the mode that first destabilises the flow at some ![]() $\varOmega$ value for
$\varOmega$ value for ![]() $\varGamma =0.1$. The purpose of this plot is to illustrate the differing strengths of the instability types, with CF modes having much larger growth rates. This plot also helps to explain the purple line surrounded by the green region in figure 4, along with the orange region appearing in the same figure.
$\varGamma =0.1$. The purpose of this plot is to illustrate the differing strengths of the instability types, with CF modes having much larger growth rates. This plot also helps to explain the purple line surrounded by the green region in figure 4, along with the orange region appearing in the same figure.
The two largest unstable regions in figure 4 demonstrate that two modes compete to destabilise the flow for the majority of parameter space. The modes with ![]() $\theta =90^\circ$, sometimes referred to as ‘Rayleigh’ modes, are the streamwise-independent portion of the CF modes induced by rotation, and they show why excellent agreement is seen with Rayleigh's criterion in figure 2. These modes give values of
$\theta =90^\circ$, sometimes referred to as ‘Rayleigh’ modes, are the streamwise-independent portion of the CF modes induced by rotation, and they show why excellent agreement is seen with Rayleigh's criterion in figure 2. These modes give values of ![]() ${ {Re}}_c$ much lower than any of the other types of modes, so the CF modes destabilise the flow first (as Reynolds number is increased) in the regions where they coexist with Tollmien–Schlichting instabilities. The instability region for the modes with
${ {Re}}_c$ much lower than any of the other types of modes, so the CF modes destabilise the flow first (as Reynolds number is increased) in the regions where they coexist with Tollmien–Schlichting instabilities. The instability region for the modes with ![]() $\theta =0^\circ$ is independent of rotation rate which can be readily seen from the equations (the vertical momentum decouples from the rest of the equations when
$\theta =0^\circ$ is independent of rotation rate which can be readily seen from the equations (the vertical momentum decouples from the rest of the equations when ![]() $k_z=0$, and a rotation-modified pressure term leads to an identical eigenvalue problem to that for
$k_z=0$, and a rotation-modified pressure term leads to an identical eigenvalue problem to that for ![]() $\varOmega =0$). These modes are guaranteed to become unstable first as the Reynolds number is increased in the non-rotating problem, by Squire's theorem (e.g. Smyth & Carpenter Reference Smyth and Carpenter2019, chapter 3), but the theorem does not hold when rotation is added, which is observed for some points around
$\varOmega =0$). These modes are guaranteed to become unstable first as the Reynolds number is increased in the non-rotating problem, by Squire's theorem (e.g. Smyth & Carpenter Reference Smyth and Carpenter2019, chapter 3), but the theorem does not hold when rotation is added, which is observed for some points around ![]() $\varOmega =0.5$.
$\varOmega =0.5$.
The behaviour seen around ![]() $\varOmega =0$ is also explained by the competition between the two mode types. First, for
$\varOmega =0$ is also explained by the competition between the two mode types. First, for ![]() $\varGamma >0.15$, the behaviour is simply explained by Rayleigh's criterion (see § 2.4), as the Tollmien–Schlichting modes are stable. For
$\varGamma >0.15$, the behaviour is simply explained by Rayleigh's criterion (see § 2.4), as the Tollmien–Schlichting modes are stable. For ![]() $\varGamma <0.15$, when
$\varGamma <0.15$, when ![]() $\varOmega =0$, the only unstable mode is the Tollmien–Schlichting mode, which explains the location of the critical
$\varOmega =0$, the only unstable mode is the Tollmien–Schlichting mode, which explains the location of the critical ![]() $\varGamma$ value where the flow changes from stable to unstable (Potter Reference Potter1966). When rotation is introduced at either side of
$\varGamma$ value where the flow changes from stable to unstable (Potter Reference Potter1966). When rotation is introduced at either side of ![]() $\varOmega =0$, even if it is incredibly small, the CF modes become unstable and their growth rates reach much larger values than those of the Tollmien–Schlichting instability. Because of this, the Tollmien–Schlichting modes were only seen to destabilise the flow first at exactly
$\varOmega =0$, even if it is incredibly small, the CF modes become unstable and their growth rates reach much larger values than those of the Tollmien–Schlichting instability. Because of this, the Tollmien–Schlichting modes were only seen to destabilise the flow first at exactly ![]() $\varOmega =0$ using the parameters of this study.
$\varOmega =0$ using the parameters of this study.
Figure 5 plots the growth rates of three chosen modes as a function of ![]() $\varOmega$, illustrating the general behaviour of a two-dimensional (2-D) CF mode, a 2-D Tollmien–Schlichting mode and a 3-D mode. The log scale of the plot illustrates clearly that the CF mode has a growth rate, for most of the range of
$\varOmega$, illustrating the general behaviour of a two-dimensional (2-D) CF mode, a 2-D Tollmien–Schlichting mode and a 3-D mode. The log scale of the plot illustrates clearly that the CF mode has a growth rate, for most of the range of ![]() $\varOmega$, that is much larger than that of the other two modes. It also demonstrates that the magnitude of
$\varOmega$, that is much larger than that of the other two modes. It also demonstrates that the magnitude of ![]() $\mathrm {d}\mathrm {Re}(\sigma )/\mathrm {d}\varOmega$ is very large for the CF instability at the edge of the range of
$\mathrm {d}\mathrm {Re}(\sigma )/\mathrm {d}\varOmega$ is very large for the CF instability at the edge of the range of ![]() $\varOmega$ where it is unstable, and so the instability jumps from having a growth rate close to its maximum to being stable with very little change of
$\varOmega$ where it is unstable, and so the instability jumps from having a growth rate close to its maximum to being stable with very little change of ![]() $\varOmega$. As expected, we observe that the 2-D Tollmien–Schlichting mode has a growth rate which is independent of
$\varOmega$. As expected, we observe that the 2-D Tollmien–Schlichting mode has a growth rate which is independent of ![]() $\varOmega$, but it is quickly overpowered with any non-zero but small
$\varOmega$, but it is quickly overpowered with any non-zero but small ![]() $\varOmega$ value by the CF mode. This is the cause of the purple line surrounded by the green region in figure 4. The plot also contains the extra instability region, shaded using orange in figure 4, as the 3-D mode has the largest growth rate for a small portion of the range of
$\varOmega$ value by the CF mode. This is the cause of the purple line surrounded by the green region in figure 4. The plot also contains the extra instability region, shaded using orange in figure 4, as the 3-D mode has the largest growth rate for a small portion of the range of ![]() $\varOmega$ values. However, even when the 3-D mode does have the largest growth rate, it is only slightly larger than that of the 2-D Tollmien–Schlichting mode, and does not reach the large values reached by the 2-D CF mode.
$\varOmega$ values. However, even when the 3-D mode does have the largest growth rate, it is only slightly larger than that of the 2-D Tollmien–Schlichting mode, and does not reach the large values reached by the 2-D CF mode.
When moving from PPF to PCF (left to right or ![]() $\varGamma \rightarrow 1$) in figure 3 for a fixed rotation rate, the critical Reynolds number drops to lower values, which is clearer for larger
$\varGamma \rightarrow 1$) in figure 3 for a fixed rotation rate, the critical Reynolds number drops to lower values, which is clearer for larger ![]() $\varOmega$ values in the unstable region. This was expected as the minimum critical Reynolds number over the range of
$\varOmega$ values in the unstable region. This was expected as the minimum critical Reynolds number over the range of ![]() $\varOmega$ values are known for both PPF and PCF to be
$\varOmega$ values are known for both PPF and PCF to be ![]() ${ {Re}}_c \approx 531$ and
${ {Re}}_c \approx 531$ and ![]() ${ {Re}}_c\approx 82.6$, respectively (e.g. Lezius & Johnston Reference Lezius and Johnston1976). The growth of the critical Reynolds number towards the boundaries of the region defined by Rayleigh's criterion therefore occurs at a much quicker rate on the right-hand side of the plot, meaning that the value of
${ {Re}}_c\approx 82.6$, respectively (e.g. Lezius & Johnston Reference Lezius and Johnston1976). The growth of the critical Reynolds number towards the boundaries of the region defined by Rayleigh's criterion therefore occurs at a much quicker rate on the right-hand side of the plot, meaning that the value of ![]() $\mathrm {d}{ {Re}}_c/\mathrm {d}\varOmega$ at
$\mathrm {d}{ {Re}}_c/\mathrm {d}\varOmega$ at ![]() $\varOmega$ values close to
$\varOmega$ values close to ![]() $0$ and
$0$ and ![]() $0.5$ increases as
$0.5$ increases as ![]() $\varGamma$ increases towards
$\varGamma$ increases towards ![]() $1$.
$1$.
Two eigenfunctions, each characteristic of one of the instability regions in figure 4, are plotted in figure 6. The Tollmien–Schlichting instability shown in figure 6(a) is one that has ![]() $k_z=0$ (i.e. the purple region), and specifically the mode is calculated and plotted for
$k_z=0$ (i.e. the purple region), and specifically the mode is calculated and plotted for ![]() $\varOmega =0$ (but note that the plotted variables,
$\varOmega =0$ (but note that the plotted variables, ![]() $\hat {u}$ and
$\hat {u}$ and ![]() $\hat {v}$, are independent of
$\hat {v}$, are independent of ![]() $\varOmega$). The CF instability eigenfunction has
$\varOmega$). The CF instability eigenfunction has ![]() $k_x=0$ and is plotted in figure 6(b) for a set of parameters somewhere in the middle of the green region. The exact parameters given in the figure caption.
$k_x=0$ and is plotted in figure 6(b) for a set of parameters somewhere in the middle of the green region. The exact parameters given in the figure caption.

Figure 6. Eigenfunctions of the different 2-D instabilities at chosen Reynolds numbers slightly above the critical values indicated in figure 3. The blue and red lines are the ![]() $\hat {u}$ and
$\hat {u}$ and ![]() $\hat {v}$ components of the velocity perturbation, with solid and dashed lines showing the real and imaginary parts. A solid grey line running horizontally shows where the eigenfunction is zero, and a vertical dashed grey line shows the location of the WKB turning point (§ 3.3). (a) Tollmien–Schlichting mode:
$\hat {v}$ components of the velocity perturbation, with solid and dashed lines showing the real and imaginary parts. A solid grey line running horizontally shows where the eigenfunction is zero, and a vertical dashed grey line shows the location of the WKB turning point (§ 3.3). (a) Tollmien–Schlichting mode: ![]() $\varGamma =0.1$,
$\varGamma =0.1$, ![]() $\varOmega =0$,
$\varOmega =0$, ![]() ${ {Re}}=200\,000$,
${ {Re}}=200\,000$, ![]() $k_x=0.8$ and
$k_x=0.8$ and ![]() $k_z=0$. (b) CF mode:
$k_z=0$. (b) CF mode: ![]() $\varGamma =0.5$,
$\varGamma =0.5$, ![]() $\varOmega =0.25$,
$\varOmega =0.25$, ![]() ${ {Re}}=500$,
${ {Re}}=500$, ![]() $k_x=0$ and
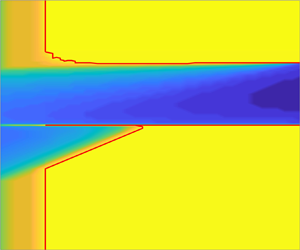
$k_x=0$ and ![]() $k_z=5.4$. The plot shows that the shape of the Tollmien–Schlichting and CF eigenfunctions are distinct (the CF eigenfunction being trapped between the wall and a WKB turning point).
$k_z=5.4$. The plot shows that the shape of the Tollmien–Schlichting and CF eigenfunctions are distinct (the CF eigenfunction being trapped between the wall and a WKB turning point).
The eigenfunctions for Tollmien–Schlichting- and CF-type instabilities are quite distinct, especially in the ![]() $\hat {u}$ variable. The Tollmien–Schlichting instability has
$\hat {u}$ variable. The Tollmien–Schlichting instability has ![]() $\hat {u}$ moving away from zero towards the boundaries before being forced to sharply return to zero close to the boundaries (due to the boundary conditions), which is very different to the behaviour of
$\hat {u}$ moving away from zero towards the boundaries before being forced to sharply return to zero close to the boundaries (due to the boundary conditions), which is very different to the behaviour of ![]() $\hat {u}$ for the CF instability. The CF instability appears to be localised at the left boundary, which is fairly weak in this case but can be much stronger in other areas of the unstable region. A dotted grey line shows the location of a WKB turning point, which is explored further in § 3.3. The distinct features of the two types of eigenfunctions will be useful when classifying the 3-D instability (orange) regions.
$\hat {u}$ for the CF instability. The CF instability appears to be localised at the left boundary, which is fairly weak in this case but can be much stronger in other areas of the unstable region. A dotted grey line shows the location of a WKB turning point, which is explored further in § 3.3. The distinct features of the two types of eigenfunctions will be useful when classifying the 3-D instability (orange) regions.
3.2. Extra 3-D instability region
The extra instability region is located around ![]() $\varGamma =0.15$ and
$\varGamma =0.15$ and ![]() $\varOmega =0.5$ in figure 3, characterised by the uneven upper-right boundary, and corresponds to a large part of the orange region in figure 4. We already know
$\varOmega =0.5$ in figure 3, characterised by the uneven upper-right boundary, and corresponds to a large part of the orange region in figure 4. We already know ![]() $k_x=0$ and
$k_x=0$ and ![]() $k_z=0$ modes must each be stable here, showing that this region only appears due to 3-D modes. Some other regions found along the line of
$k_z=0$ modes must each be stable here, showing that this region only appears due to 3-D modes. Some other regions found along the line of ![]() $\varGamma$ (approaching
$\varGamma$ (approaching ![]() $\varOmega =0.5$ from below) are also first destabilised by 3-D modes.
$\varOmega =0.5$ from below) are also first destabilised by 3-D modes.
In order to identify the origin of the extra instability region, the spectrums of growth rates are plotted in figures 7 and 8 over wavenumber space for varying ![]() $\varGamma$ and
$\varGamma$ and ![]() $\varOmega$. Starting with figure 7(a), the parameter values are
$\varOmega$. Starting with figure 7(a), the parameter values are ![]() $\varGamma =0$ and
$\varGamma =0$ and ![]() $\varOmega =0$ (and
$\varOmega =0$ (and ![]() ${ {Re}}=10^6$, fixed for the sequence of plots), which is non-rotating PPF. The branch of instability seen in this plot is the well-known Tollmien–Schlichting instability. In figure 7,
${ {Re}}=10^6$, fixed for the sequence of plots), which is non-rotating PPF. The branch of instability seen in this plot is the well-known Tollmien–Schlichting instability. In figure 7, ![]() $\varOmega$ is gradually increased to
$\varOmega$ is gradually increased to ![]() $\varOmega =0.5$ in 7(f). During this transition, the Tollmien–Schlichting branch of instability can be easily tracked and is the only instability that persists at
$\varOmega =0.5$ in 7(f). During this transition, the Tollmien–Schlichting branch of instability can be easily tracked and is the only instability that persists at ![]() $\varGamma =0$,
$\varGamma =0$, ![]() $\varOmega =0.5$. Along the way, a CF instability is observed to appear in the top left (attached to
$\varOmega =0.5$. Along the way, a CF instability is observed to appear in the top left (attached to ![]() $k_x=0$), but disappears again as expected by Rayleigh's criterion. Figure 8 increases
$k_x=0$), but disappears again as expected by Rayleigh's criterion. Figure 8 increases ![]() $\varGamma$ gradually from
$\varGamma$ gradually from ![]() $0$ to
$0$ to ![]() $0.2$, and the Tollmien–Schlichting branch can be clearly tracked as
$0.2$, and the Tollmien–Schlichting branch can be clearly tracked as ![]() $\varGamma$ is increased. As this happens, the most unstable mode moves away from
$\varGamma$ is increased. As this happens, the most unstable mode moves away from ![]() $k_z=0$, as indicated by the red cross in the plots. Beyond
$k_z=0$, as indicated by the red cross in the plots. Beyond ![]() $\varGamma =0.15$, the
$\varGamma =0.15$, the ![]() $k_z=0$ modes are stable as expected, so the branch moves away from that axis. The instability at this point in parameter space can therefore be categorised as a modified Tollmien–Schlichting instability, originating from the regular Tollmien–Schlichting instability, but its most unstable wavenumbers and the critical
$k_z=0$ modes are stable as expected, so the branch moves away from that axis. The instability at this point in parameter space can therefore be categorised as a modified Tollmien–Schlichting instability, originating from the regular Tollmien–Schlichting instability, but its most unstable wavenumbers and the critical ![]() $\varGamma$ at which it becomes stable are altered by the presence of rotation. The eigenfunction shown in figure 9 supports the classification of the 3-D mode at
$\varGamma$ at which it becomes stable are altered by the presence of rotation. The eigenfunction shown in figure 9 supports the classification of the 3-D mode at ![]() $\varGamma =0.2$,
$\varGamma =0.2$, ![]() $\varOmega =0.5$ as a Tollmien–Schlichting-type instability, showing clear similarities with the Tollmien–Schlichting eigenfunction shown in figure 6(a).
$\varOmega =0.5$ as a Tollmien–Schlichting-type instability, showing clear similarities with the Tollmien–Schlichting eigenfunction shown in figure 6(a).

Figure 7. Contour plots showing the growth rate of the most unstable mode at different points in the space of wavenumbers, where the ![]() $\varOmega$ value changes gradually from
$\varOmega$ value changes gradually from ![]() $0$ to
$0$ to ![]() $0.5$ as the plots run from (a) to (f), with other parameter values fixed at
$0.5$ as the plots run from (a) to (f), with other parameter values fixed at ![]() $\varGamma =0$,
$\varGamma =0$, ![]() ${ {Re}}=10^6$. White space indicates that the wavenumber pair is stable. The triangular instability region in the top left is CF instability, whereas the region attached to the
${ {Re}}=10^6$. White space indicates that the wavenumber pair is stable. The triangular instability region in the top left is CF instability, whereas the region attached to the ![]() $k_x$-axis is Tollmien–Schlichting instability. This transition traces out the vertical black line in figure 4. This figure allows the known Tollmien–Schlichting branch to be tracked to larger rotation rates, which aids in identifying the mode types for arbitrary
$k_x$-axis is Tollmien–Schlichting instability. This transition traces out the vertical black line in figure 4. This figure allows the known Tollmien–Schlichting branch to be tracked to larger rotation rates, which aids in identifying the mode types for arbitrary ![]() $\varGamma$ and
$\varGamma$ and ![]() $\varOmega$.
$\varOmega$.

Figure 8. Same as figure 7, but now ![]() $\varGamma$ changes gradually from
$\varGamma$ changes gradually from ![]() $0$ to
$0$ to ![]() $0.2$, with other parameters fixed at
$0.2$, with other parameters fixed at ![]() $\varOmega =0.5$,
$\varOmega =0.5$, ![]() ${ {Re}}=10^6$. Figure 7(f) is identical to (a). The red cross indicates where the most unstable mode is, which does not appear in (a) as the most unstable mode has
${ {Re}}=10^6$. Figure 7(f) is identical to (a). The red cross indicates where the most unstable mode is, which does not appear in (a) as the most unstable mode has ![]() $k_z=0$, and here we use log scale axes. This transition traces out the horizontal black line in figure 4. This figure further tracks the Tollmien–Schlichting branch to non-zero values of
$k_z=0$, and here we use log scale axes. This transition traces out the horizontal black line in figure 4. This figure further tracks the Tollmien–Schlichting branch to non-zero values of ![]() $\varGamma$, showing the instability found at
$\varGamma$, showing the instability found at ![]() $\varGamma =0.2$,
$\varGamma =0.2$, ![]() $\varOmega =0.5$ is a modified Tollmien–Schlichting instability.
$\varOmega =0.5$ is a modified Tollmien–Schlichting instability.

Figure 9. Same as figure 6, but with parameters ![]() $\varGamma =0.2$,
$\varGamma =0.2$, ![]() $\varOmega =0.5$,
$\varOmega =0.5$, ![]() ${ {Re}}=10^6$,
${ {Re}}=10^6$, ![]() $k_x=1$ and
$k_x=1$ and ![]() $k_z=0.55$. This figure shows a similar eigenfunction structure to that shown in figure 6(a), and so further supports the classification of this mode as a Tollmien–Schlichting instability.
$k_z=0.55$. This figure shows a similar eigenfunction structure to that shown in figure 6(a), and so further supports the classification of this mode as a Tollmien–Schlichting instability.
This modified Tollmien–Schlichting instability does not account for all of the orange instability region seen in figure 4, especially towards the larger ![]() $\varGamma$ values. Figure 10 again displays the growth rates in wavenumber space, this time for a fixed pair of
$\varGamma$ values. Figure 10 again displays the growth rates in wavenumber space, this time for a fixed pair of ![]() $\varGamma =0.4$ and
$\varGamma =0.4$ and ![]() $\varOmega =0.4875$, with varying Reynolds number. The first plot shows not only that the most unstable mode is a 3-D mode, but, in fact, only the 3-D modes are unstable at
$\varOmega =0.4875$, with varying Reynolds number. The first plot shows not only that the most unstable mode is a 3-D mode, but, in fact, only the 3-D modes are unstable at ![]() ${ {Re}}=5\times 10^5$. However, as
${ {Re}}=5\times 10^5$. However, as ![]() ${ {Re}}$ is increased, a branch extending from
${ {Re}}$ is increased, a branch extending from ![]() $k_x=0$ appears and becomes unstable, before the branches merge at even larger
$k_x=0$ appears and becomes unstable, before the branches merge at even larger ![]() ${ {Re}}$ number and the most unstable mode moves to the
${ {Re}}$ number and the most unstable mode moves to the ![]() $k_x=0$-axis. This transition of the most unstable mode is indicated by the red cross appearing in the plots, which is absent in the final plot as
$k_x=0$-axis. This transition of the most unstable mode is indicated by the red cross appearing in the plots, which is absent in the final plot as ![]() $k_x=0$ is not plotted on the log-scale axes. These modes are classified as a viscosity-modified CF instability.
$k_x=0$ is not plotted on the log-scale axes. These modes are classified as a viscosity-modified CF instability.

Figure 10. Similar contour plots of the growth rate to those presented in figure 7. The constant parameters across these (a–c) are ![]() $\varGamma =0.4$ and
$\varGamma =0.4$ and ![]() $\varOmega =0.4875$ (indicated by a black dot in figure 4), with the Reynolds number given above each plot. The red cross once again shows the location of the most unstable mode, and is not present in (c) as the most unstable mode has
$\varOmega =0.4875$ (indicated by a black dot in figure 4), with the Reynolds number given above each plot. The red cross once again shows the location of the most unstable mode, and is not present in (c) as the most unstable mode has ![]() $k_x=0$. The figure shows a transition of the instability branch in (a) to larger Reynolds numbers, where the instability becomes part of the CF branch and the most unstable mode moves to
$k_x=0$. The figure shows a transition of the instability branch in (a) to larger Reynolds numbers, where the instability becomes part of the CF branch and the most unstable mode moves to ![]() $k_x=0$. This suggests the instability at
$k_x=0$. This suggests the instability at ![]() $\varGamma =0.4$,
$\varGamma =0.4$, ![]() $\varOmega =0.4875$ and
$\varOmega =0.4875$ and ![]() ${ {Re}}=500\,000$ is a CF-type instability, modified by the effects of viscosity.
${ {Re}}=500\,000$ is a CF-type instability, modified by the effects of viscosity.
The eigenfunction again supports the classification, this time as a CF-type mode. The eigenfunction for the most unstable mode at the point ![]() $\varGamma =0.4$,
$\varGamma =0.4$, ![]() $\varOmega =0.4875$ (with
$\varOmega =0.4875$ (with ![]() ${ {Re}}=500\,000$) is shown in figure 11(a), and displays an oscillatory structure with decay beyond the vertical line (which indicates the WKB turning point), similar to the mode shown in figure 6(b). Although this time the localisation at the left boundary is much stronger, the mode is observed to share more similarities with the CF mode of figure 6 than the Tollmien–Schlichting mode shown in the same figure. In figure 11(b), as a further example for the orange region closer to
${ {Re}}=500\,000$) is shown in figure 11(a), and displays an oscillatory structure with decay beyond the vertical line (which indicates the WKB turning point), similar to the mode shown in figure 6(b). Although this time the localisation at the left boundary is much stronger, the mode is observed to share more similarities with the CF mode of figure 6 than the Tollmien–Schlichting mode shown in the same figure. In figure 11(b), as a further example for the orange region closer to ![]() $\varGamma =1$, the eigenfunction is shown for a 3-D mode instability at the point
$\varGamma =1$, the eigenfunction is shown for a 3-D mode instability at the point ![]() $\varGamma =0.975$,
$\varGamma =0.975$, ![]() $\varOmega =0.49375$, which again has similarities with the CF mode already presented above, and this time the localisation is weaker.
$\varOmega =0.49375$, which again has similarities with the CF mode already presented above, and this time the localisation is weaker.

Figure 11. Same as figure 6, but with parameters (a) ![]() $\varGamma =0.4$,
$\varGamma =0.4$, ![]() $\varOmega =0.4875$,
$\varOmega =0.4875$, ![]() ${ {Re}}=500\,000$,
${ {Re}}=500\,000$, ![]() $k_x=5$ and
$k_x=5$ and ![]() $k_z=63$, and (b)
$k_z=63$, and (b) ![]() $\varGamma =0.975$,
$\varGamma =0.975$, ![]() $\varOmega =0.49375$,
$\varOmega =0.49375$, ![]() ${ {Re}}=5000$,
${ {Re}}=5000$, ![]() $k_x=0.3$ and
$k_x=0.3$ and ![]() $k_z=6$. This figure shows that the eigenfunction structure of the 3-D mode instability investigated in figure 10 has similarities with that of figure 6(b), further suggesting it is of CF type. It also demonstrates this for a further example of an identified 3-D mode instability.
$k_z=6$. This figure shows that the eigenfunction structure of the 3-D mode instability investigated in figure 10 has similarities with that of figure 6(b), further suggesting it is of CF type. It also demonstrates this for a further example of an identified 3-D mode instability.
The eigenfunctions are a quick way to classify whether the 3-D mode is a modified Tollmien–Schlichting or CF type. The modified Tollmien–Schlichting instability is expected to exist only close to ![]() $\varGamma =0.15$, and so it is likely that the 3-D mode regions for larger
$\varGamma =0.15$, and so it is likely that the 3-D mode regions for larger ![]() $\varGamma$ values are due to the finite Reynolds number effects and the CF instability. Both types of 3-D mode instabilities seem to prefer anticyclonic rotation, and so are not observed towards the bottom of the unstable region.
$\varGamma$ values are due to the finite Reynolds number effects and the CF instability. Both types of 3-D mode instabilities seem to prefer anticyclonic rotation, and so are not observed towards the bottom of the unstable region.
The instability branches seen in figure 8(f) and figure 10(a) are very small in wavenumber space, suggesting a more fine wavenumber resolution is required to fully capture these instabilities. This is the reason that the 3-D mode regions (orange in figure 4) appear to exist in a quite patchy and random manner. Here we have had to sacrifice the resolution in wavenumber to be able to investigate a broad range of other parameters.
3.3. Semi-localised eigenfunctions
An interesting trend in the numerical data (used to plot figure 3) is that as the parameters are changed and moved towards the edge of the CF instability region (e.g. ![]() $\varOmega$ is moved towards
$\varOmega$ is moved towards ![]() $0.5$ from below), the
$0.5$ from below), the ![]() $k_z$ wavenumber of the destabilising mode increases alongside the critical Reynolds number. The latter indicates that the instability can be captured by an inviscid approximation in which the governing eigenvalue problem given by (2.7)–(2.12) reduces to a simple second-order ordinary differential equation (ODE) for
$k_z$ wavenumber of the destabilising mode increases alongside the critical Reynolds number. The latter indicates that the instability can be captured by an inviscid approximation in which the governing eigenvalue problem given by (2.7)–(2.12) reduces to a simple second-order ordinary differential equation (ODE) for ![]() $\hat {v}$ (recall
$\hat {v}$ (recall ![]() ${ {Pr}}=\infty$,
${ {Pr}}=\infty$, ![]() $N=0$ and
$N=0$ and ![]() $\hat {\rho }=0$, so (2.11) is not needed):
$\hat {\rho }=0$, so (2.11) is not needed):
(see Billant & Gallaire (Reference Billant and Gallaire2005) for an equivalent cylindrical base flow expression). The fact that ![]() $k_z \gg 1$ means that a WKB (short-wavelength) approximation can also be used. The numerical results show that the frequency is consistently many orders of magnitude smaller than the growth rate, so that
$k_z \gg 1$ means that a WKB (short-wavelength) approximation can also be used. The numerical results show that the frequency is consistently many orders of magnitude smaller than the growth rate, so that ![]() $\sigma _i \ll \sigma _r$, and we will use
$\sigma _i \ll \sigma _r$, and we will use ![]() $\sigma \simeq \sigma _r$ in the following. The nature of the solution is determined by the sign of the function
$\sigma \simeq \sigma _r$ in the following. The nature of the solution is determined by the sign of the function ![]() $b(y)$: positive and the solution is oscillatory in space, negative and the solution is exponentially growing/decaying. Because of this, a location of
$b(y)$: positive and the solution is oscillatory in space, negative and the solution is exponentially growing/decaying. Because of this, a location of ![]() $y$ where
$y$ where ![]() $b(y)=0$ (a WKB turning point
$b(y)=0$ (a WKB turning point ![]() $y_t$) causes a change in behaviour of the solution. When there is only one turning point in the domain, which is the case here as
$y_t$) causes a change in behaviour of the solution. When there is only one turning point in the domain, which is the case here as ![]() $U_B'$ is only linear in
$U_B'$ is only linear in ![]() $y$ so
$y$ so
the oscillatory or wave-like part of the solution can be trapped on one of the channel walls, and is referred to as being ‘semi-localised’. In order to have fully localised unstable modes, two turning points are needed within the domain, with oscillatory behaviour between them and decay towards each wall. A cubic base flow is sufficient to force the two turning points, as then ![]() $U_B'$ is quadratic in
$U_B'$ is quadratic in ![]() $y$. Appendix C demonstrates that localised CF modes exist for a cubic base flow that remains close to a simple PCF.
$y$. Appendix C demonstrates that localised CF modes exist for a cubic base flow that remains close to a simple PCF.
For the CPF problem, further CF eigenfunctions are plotted in figure 12 at ![]() $\varGamma =0.1$ and
$\varGamma =0.1$ and ![]() $\varOmega =0.25,0.45$, with a dotted grey line showing the turning point. There is a good match with the localisation observed in both eigenfunctions. It can be seen directly from (3.2) that for fixed
$\varOmega =0.25,0.45$, with a dotted grey line showing the turning point. There is a good match with the localisation observed in both eigenfunctions. It can be seen directly from (3.2) that for fixed ![]() $\varGamma =0.1$, stronger localisation is found for larger
$\varGamma =0.1$, stronger localisation is found for larger ![]() $\varOmega$. For larger
$\varOmega$. For larger ![]() $\varGamma$ values, taking
$\varGamma$ values, taking ![]() $\varOmega$ too small results in
$\varOmega$ too small results in ![]() $y_t>1$ and no localisation is observed. The turning point location in (3.2) estimates the localisation of the eigenfunctions very well even for the CF modes of figures 6 and 11, where
$y_t>1$ and no localisation is observed. The turning point location in (3.2) estimates the localisation of the eigenfunctions very well even for the CF modes of figures 6 and 11, where ![]() $k_z$ is not so large. WKB solutions can also be found for
$k_z$ is not so large. WKB solutions can also be found for ![]() $k_x >0$ but then the turning points are in the complex plane and the analysis more delicate (Billant & Gallaire Reference Billant and Gallaire2005). Analytical solutions are also available in the streamwise-independent, inviscid and linear CPF problem as a linear combination of Airy functions, but this is not pursued here.
$k_x >0$ but then the turning points are in the complex plane and the analysis more delicate (Billant & Gallaire Reference Billant and Gallaire2005). Analytical solutions are also available in the streamwise-independent, inviscid and linear CPF problem as a linear combination of Airy functions, but this is not pursued here.

Figure 12. Same as figure 6, but with parameters (a) ![]() $\varGamma =0.1$,
$\varGamma =0.1$, ![]() $\varOmega =0.25$,
$\varOmega =0.25$, ![]() ${ {Re}}=1000$,
${ {Re}}=1000$, ![]() $k_x=0$ and
$k_x=0$ and ![]() $k_z=7.8$, and (b)
$k_z=7.8$, and (b) ![]() $\varGamma =0.1$,
$\varGamma =0.1$, ![]() $\varOmega =0.45$,
$\varOmega =0.45$, ![]() ${ {Re}}=60\,000$,
${ {Re}}=60\,000$, ![]() $k_x=0$,
$k_x=0$, ![]() $k_z=46$. The displayed eigenfunctions demonstrate how the trapping length scale of the mode between a WKB turning point and the wall is highly dependent on the parameters.
$k_z=46$. The displayed eigenfunctions demonstrate how the trapping length scale of the mode between a WKB turning point and the wall is highly dependent on the parameters.
All the eigenfunctions shown are localised on the left wall, and this can be directly observed from the WKB governing equation. In fact, rewriting the function ![]() $b(y)$ using
$b(y)$ using ![]() $y_t$ gives
$y_t$ gives
For the localisation of an unstable mode to occur on the left-hand (right-hand) side of the channel, the sign of ![]() $b(y)$ would have to be positive for
$b(y)$ would have to be positive for ![]() $y< y_t$ (
$y< y_t$ (![]() $y>y_t$). Observe then that localisation occurs on the left-hand side of the channel for anticyclonic rotation (
$y>y_t$). Observe then that localisation occurs on the left-hand side of the channel for anticyclonic rotation (![]() $\varOmega >0$), whereas localisation occurs on the right-hand side of the channel for cyclonic rotation (
$\varOmega >0$), whereas localisation occurs on the right-hand side of the channel for cyclonic rotation (![]() $\varOmega <0$). Semi-localised CF eigenfunctions (i.e. those that are trapped on one side of the domain, decaying towards the opposite wall) have already been identified in the literature (e.g. Leclercq et al. Reference Leclercq, Nguyen and Kerswell2016; Park et al. Reference Park, Billant and Baik2017, Reference Park, Billant, Baik and Seo2018).
$\varOmega <0$). Semi-localised CF eigenfunctions (i.e. those that are trapped on one side of the domain, decaying towards the opposite wall) have already been identified in the literature (e.g. Leclercq et al. Reference Leclercq, Nguyen and Kerswell2016; Park et al. Reference Park, Billant and Baik2017, Reference Park, Billant, Baik and Seo2018).
4. Numerical results II: instabilities in stratified, rotating CPF
For both rotating and non-rotating shear flows, the introduction of stratification can destabilise the flow by introducing resonance instabilities (Yavneh et al. Reference Yavneh, McWilliams and Molemaker2001; Dubrulle et al. Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005; Vanneste & Yavneh Reference Vanneste and Yavneh2007; Facchini et al. Reference Facchini, Favier, Le Gal, Wang and Le Bars2018; Le Gal et al. Reference Le Gal, Harlander, Borcia, Le Dizès, Chen and Favier2021). These instabilities take the form of very thin branches in wavenumber space, so that for a fixed horizontal wavenumber, only a small range of vertical wavenumbers is unstable. In order to capture these instabilities, a much higher resolution in the wavenumbers is needed than that used in the previous section for unstratified flow. Because of this, the resolution across other parameters is reduced for practical reasons. For most of this section, ![]() $N=2$ and
$N=2$ and ![]() ${ {Pr}}=\infty$ are selected to represent moderate stratification. The rotation rate of the Earth is
${ {Pr}}=\infty$ are selected to represent moderate stratification. The rotation rate of the Earth is ![]() $1.16\times 10^{-5}\,\mathrm {s}^{-1}$ and the (dimensional) buoyancy frequency can typically reach the order of
$1.16\times 10^{-5}\,\mathrm {s}^{-1}$ and the (dimensional) buoyancy frequency can typically reach the order of ![]() $10^{-2}\,\mathrm {s}^{-1}$ in the oceans or atmosphere, meaning
$10^{-2}\,\mathrm {s}^{-1}$ in the oceans or atmosphere, meaning ![]() $2\varOmega /N < 1$ is typically satisfied (e.g. Vanneste & Yavneh Reference Vanneste and Yavneh2007; Cushman-Roisin & Beckers Reference Cushman-Roisin and Beckers2011, chapter 11; Vallis Reference Vallis2017, chapter 2). For this reason, we use
$2\varOmega /N < 1$ is typically satisfied (e.g. Vanneste & Yavneh Reference Vanneste and Yavneh2007; Cushman-Roisin & Beckers Reference Cushman-Roisin and Beckers2011, chapter 11; Vallis Reference Vallis2017, chapter 2). For this reason, we use ![]() ${\left |\varOmega \right |}\leq 1$ in order to stay in a physically relevant regime, where stratification is stronger than rotation.
${\left |\varOmega \right |}\leq 1$ in order to stay in a physically relevant regime, where stratification is stronger than rotation.
Analysis of rotating and stratified PPF and PCF, in terms of what instabilities persist to finite Reynolds numbers, is not something that has been explored in detail. To start our investigation of stratified, rotating CPF, we therefore focus on PCF and PPF with varying ![]() $\varOmega$. We then look at two fixed
$\varOmega$. We then look at two fixed ![]() $\varOmega$ values with varying
$\varOmega$ values with varying ![]() $\varGamma$, in order to probe how the instabilities that are supported change with
$\varGamma$, in order to probe how the instabilities that are supported change with ![]() $\varGamma$, and to give an idea of how PCF and PPF are connected in parameter space. This also guides the choice of
$\varGamma$, and to give an idea of how PCF and PPF are connected in parameter space. This also guides the choice of ![]() $\varGamma =0.75$, which we studied in detail in the same way as
$\varGamma =0.75$, which we studied in detail in the same way as ![]() $\varGamma =0$ and
$\varGamma =0$ and ![]() $\varGamma =1$. Figure 13 displays the points, in a 3-D parameter space of
$\varGamma =1$. Figure 13 displays the points, in a 3-D parameter space of ![]() $\varGamma$,
$\varGamma$, ![]() $\varOmega$ and
$\varOmega$ and ![]() $N$, that are explored in this section. We finish with an exploration of the effects of strong stratification and thermal diffusion.
$N$, that are explored in this section. We finish with an exploration of the effects of strong stratification and thermal diffusion.

Figure 13. Plot of the 3-D parameter space of ![]() $\varGamma$,
$\varGamma$, ![]() $\varOmega$ and
$\varOmega$ and ![]() $N$. The black points are parameter settings where data were collected, whereas the coloured annotations detail which points in parameter space are used for subsequent figures. The grey shaded region at the base of the plot is Rayleigh's region, which was presented in figure 2, and shows the unstable region for streamwise-independent perturbations, valid for any
$N$. The black points are parameter settings where data were collected, whereas the coloured annotations detail which points in parameter space are used for subsequent figures. The grey shaded region at the base of the plot is Rayleigh's region, which was presented in figure 2, and shows the unstable region for streamwise-independent perturbations, valid for any ![]() $N$ value (i.e. valid anywhere directly above the shaded region).
$N$ value (i.e. valid anywhere directly above the shaded region).
4.1. Anticyclonic rotation ( $\varOmega >0$)
$\varOmega >0$)
To probe the instability types found for anticyclonic rotation, and the relative strength of the instabilities, growth rate spectrums over wavenumber space are presented. Figure 14 shows six different plots, which vary the rotation rate from ![]() $0$ to
$0$ to ![]() $1$ for PPF (
$1$ for PPF (![]() $\varGamma =0$). Four branches of instability are seen in the non-rotating flow, in good agreement with the results shown in figure 4.12 of Chen (Reference Chen2016) and figure 6 of Le Gal et al. (Reference Le Gal, Harlander, Borcia, Le Dizès, Chen and Favier2021), corresponding to the non-rotating flow (
$\varGamma =0$). Four branches of instability are seen in the non-rotating flow, in good agreement with the results shown in figure 4.12 of Chen (Reference Chen2016) and figure 6 of Le Gal et al. (Reference Le Gal, Harlander, Borcia, Le Dizès, Chen and Favier2021), corresponding to the non-rotating flow (![]() $\varOmega =0$). They identify the branch extending from
$\varOmega =0$). They identify the branch extending from ![]() $k_z=0$ as a Tollmien–Schlichting instability, whereas the other branches correspond to resonance instabilities between Tollmien–Schlichting modes and IGWs. The Tollmien–Schlichting instability branch remains as
$k_z=0$ as a Tollmien–Schlichting instability, whereas the other branches correspond to resonance instabilities between Tollmien–Schlichting modes and IGWs. The Tollmien–Schlichting instability branch remains as ![]() $\varOmega$ increases, but reduces in size as
$\varOmega$ increases, but reduces in size as ![]() $\varOmega$ approaches
$\varOmega$ approaches ![]() $1$. This branch requires no further study in the presence of stratification. The stratification plays no part in the eigenvalue problem for the
$1$. This branch requires no further study in the presence of stratification. The stratification plays no part in the eigenvalue problem for the ![]() $k_z=0$ modes, and introducing a non-zero
$k_z=0$ modes, and introducing a non-zero ![]() $k_z$ does not qualitatively change the eigenfunctions. A large unstable branch appears for rotating PPF, attached to
$k_z$ does not qualitatively change the eigenfunctions. A large unstable branch appears for rotating PPF, attached to ![]() $k_x=0$ for smaller rotation rates, and it is much more unstable than the Tollmien–Schlichting instability, although it stabilises again as
$k_x=0$ for smaller rotation rates, and it is much more unstable than the Tollmien–Schlichting instability, although it stabilises again as ![]() $\varOmega$ approaches
$\varOmega$ approaches ![]() $1$.
$1$.

Figure 14. A sequence of growth rate plots over wavenumber space. The rotation rate increases going from (a) to (f). For this sequence, the flow is PPF (![]() $\varGamma =0$),
$\varGamma =0$), ![]() $N=2$ and
$N=2$ and ![]() ${ {Re}}=50\,000$. White space is plotted where the wavenumber pairs are stable. This figure demonstrates how the large instability branch is stabilised with increasing
${ {Re}}=50\,000$. White space is plotted where the wavenumber pairs are stable. This figure demonstrates how the large instability branch is stabilised with increasing ![]() $\varOmega$, but the small thin branch connected to
$\varOmega$, but the small thin branch connected to ![]() $k_z=0$ (identified as a Tollmien–Schlichting instability) is present for all rotation rates.
$k_z=0$ (identified as a Tollmien–Schlichting instability) is present for all rotation rates.
This large branch is expected to be a stratification-modified CF instability, due to the connection with the unstable ![]() $k_x=0$ modes and its stabilisation for larger
$k_x=0$ modes and its stabilisation for larger ![]() $\varOmega$ values. To investigate and confirm its origin, it is useful to look at its transition as non-zero
$\varOmega$ values. To investigate and confirm its origin, it is useful to look at its transition as non-zero ![]() $N$ is introduced and increased towards
$N$ is introduced and increased towards ![]() $2$. This is presented for
$2$. This is presented for ![]() $\varOmega =0.2$ in figure 15. In the unstratified flow, we see two types of instability from the previous section: Tollmien–Schlichting and CF. The CF branch dominates wavenumber space and has larger growth rates. As
$\varOmega =0.2$ in figure 15. In the unstratified flow, we see two types of instability from the previous section: Tollmien–Schlichting and CF. The CF branch dominates wavenumber space and has larger growth rates. As ![]() $N$ is increased, the branch shrinks, with more wavenumber pairs stabilised by increasing
$N$ is increased, the branch shrinks, with more wavenumber pairs stabilised by increasing ![]() $N$, but clearly the large unstable branch in figure 14 has evolved from the CF branch, and is classified as a stratification-modified CF instability. The evolution of this branch displays the feature that for strong enough
$N$, but clearly the large unstable branch in figure 14 has evolved from the CF branch, and is classified as a stratification-modified CF instability. The evolution of this branch displays the feature that for strong enough ![]() $N$, the most unstable mode moves from away
$N$, the most unstable mode moves from away ![]() $k_x=0$.
$k_x=0$.

Figure 15. A sequence of growth rate plots over wavenumber space. The buoyancy frequency ![]() $N$ increases going from (a) to (f). For this sequence, the flow is PPF (i.e.
$N$ increases going from (a) to (f). For this sequence, the flow is PPF (i.e. ![]() $\varGamma =0$),
$\varGamma =0$), ![]() $\varOmega =0.2$ and
$\varOmega =0.2$ and ![]() ${ {Re}}=50\,000$. White space is plotted where the wavenumber pairs are stable. This figure aids in classifying the large instability branch found in figure 14 as a stratification-modified CF instability, by showing a transition of the instability branches in wavenumber space as stratification is introduced and gradually increased (as the instability types are known for the unstratified flow).
${ {Re}}=50\,000$. White space is plotted where the wavenumber pairs are stable. This figure aids in classifying the large instability branch found in figure 14 as a stratification-modified CF instability, by showing a transition of the instability branches in wavenumber space as stratification is introduced and gradually increased (as the instability types are known for the unstratified flow).
The transition from ![]() $\varOmega =0.4$ to
$\varOmega =0.4$ to ![]() $\varOmega =0.6$ in figure 14 crosses the critical
$\varOmega =0.6$ in figure 14 crosses the critical ![]() $\varOmega$ where Rayleigh's criterion states that the flow should become stable to streamwise-independent perturbations (even for stratified flow, see Appendix B), and this is observed as the branch moves away from the axis.
$\varOmega$ where Rayleigh's criterion states that the flow should become stable to streamwise-independent perturbations (even for stratified flow, see Appendix B), and this is observed as the branch moves away from the axis.
Figure 16 shows the eigenfunctions for the most unstable wavenumber pairs of the ![]() $\varOmega =0.2,0.4$ and
$\varOmega =0.2,0.4$ and ![]() $0.6$ plots in figure 14. The branch for
$0.6$ plots in figure 14. The branch for ![]() $\varOmega =0.2$ was identified to be a CF-type instability, and the eigenfunction in figure 16(a) clearly supports that when comparing it to a characteristic CF-type eigenfunction in the unstratified flow, for example figure 12(a) (or when comparing with CF modes identified in the literature, e.g. Park et al. Reference Park, Billant and Baik2017, Reference Park, Billant, Baik and Seo2018). The short transition first to
$\varOmega =0.2$ was identified to be a CF-type instability, and the eigenfunction in figure 16(a) clearly supports that when comparing it to a characteristic CF-type eigenfunction in the unstratified flow, for example figure 12(a) (or when comparing with CF modes identified in the literature, e.g. Park et al. Reference Park, Billant and Baik2017, Reference Park, Billant, Baik and Seo2018). The short transition first to ![]() $\varOmega =0.4$ and then to
$\varOmega =0.4$ and then to ![]() $\varOmega =0.6$ shows that, although the qualitative structure is somewhat different for
$\varOmega =0.6$ shows that, although the qualitative structure is somewhat different for ![]() $\varOmega =0.6$, it is, in fact, the same type of mode. We also still see the localisation on one side of the domain. This is expected for stratified CF instability with
$\varOmega =0.6$, it is, in fact, the same type of mode. We also still see the localisation on one side of the domain. This is expected for stratified CF instability with ![]() $k_x=0$, as the analysis of § 3.3 can be easily modified to include the effects of stratification Billant & Gallaire (Reference Billant and Gallaire2005). Despite non-zero
$k_x=0$, as the analysis of § 3.3 can be easily modified to include the effects of stratification Billant & Gallaire (Reference Billant and Gallaire2005). Despite non-zero ![]() $k_x$ here, we still observe the localisation, which supports the argument that these branches of instability in the plots of figure 14 can be classified as CF-type instabilities. Finally, the discussion in Appendix D further supports the classification of these modes as CF-type instabilities, as we do not see interactions between frequency branches, or thin ranges of instability in
$k_x$ here, we still observe the localisation, which supports the argument that these branches of instability in the plots of figure 14 can be classified as CF-type instabilities. Finally, the discussion in Appendix D further supports the classification of these modes as CF-type instabilities, as we do not see interactions between frequency branches, or thin ranges of instability in ![]() $k_z$. A CF-type instability modified by stratification is therefore observed beyond the Rayleigh line. Interestingly, this instability cannot be captured by a WKB analysis with
$k_z$. A CF-type instability modified by stratification is therefore observed beyond the Rayleigh line. Interestingly, this instability cannot be captured by a WKB analysis with ![]() $k_x>0$ as stratification is only found to play a secondary role there (Billant & Gallaire Reference Billant and Gallaire2005). This indicates that there is no
$k_x>0$ as stratification is only found to play a secondary role there (Billant & Gallaire Reference Billant and Gallaire2005). This indicates that there is no ![]() $k_z \rightarrow \infty$ limit for these stratification-modified CF instabilities.
$k_z \rightarrow \infty$ limit for these stratification-modified CF instabilities.

Figure 16. Eigenfunctions of the most unstable mode for parameter values ![]() $\varGamma =0$,
$\varGamma =0$, ![]() $N=2$,
$N=2$, ![]() ${ {Re}}=50\,000$, along with (a)
${ {Re}}=50\,000$, along with (a) ![]() $\varOmega =0.2$,
$\varOmega =0.2$, ![]() $k_x=2.4$ and
$k_x=2.4$ and ![]() $k_z=59.6$, (b)
$k_z=59.6$, (b) ![]() $\varOmega =0.4$,
$\varOmega =0.4$, ![]() $k_x=4$ and
$k_x=4$ and ![]() $k_z=45.9$ and (c)
$k_z=45.9$ and (c) ![]() $\varOmega =0.6$,
$\varOmega =0.6$, ![]() $k_x=3.2$ and
$k_x=3.2$ and ![]() $k_z=30$. The blue and red lines are the
$k_z=30$. The blue and red lines are the ![]() $\hat {u}$ and
$\hat {u}$ and ![]() $\hat {v}$ components of the velocity perturbation, with solid and dashed lines showing the real and imaginary parts. The plots are only shown up to
$\hat {v}$ components of the velocity perturbation, with solid and dashed lines showing the real and imaginary parts. The plots are only shown up to ![]() $y=0.6$ as the eigenfunctions decay to zero. This figure shows, first, that for smaller
$y=0.6$ as the eigenfunctions decay to zero. This figure shows, first, that for smaller ![]() $\varOmega$ the qualitative shape of the eigenfunctions is similar to the CF modes in the unstratified flow (e.g. figure 12a) and, second, that the gradual change in shape allows the same classification to be made for the instabilities at larger
$\varOmega$ the qualitative shape of the eigenfunctions is similar to the CF modes in the unstratified flow (e.g. figure 12a) and, second, that the gradual change in shape allows the same classification to be made for the instabilities at larger ![]() $\varOmega$ values.
$\varOmega$ values.
The ‘ripple’-type feature near the CF branch in the ![]() $\varOmega =0.2$ plot of figure 14 looks like a candidate for a resonance instability, as the literature shows that the resonance mechanism leads to small unstable
$\varOmega =0.2$ plot of figure 14 looks like a candidate for a resonance instability, as the literature shows that the resonance mechanism leads to small unstable ![]() $k_z$ ranges for a chosen
$k_z$ ranges for a chosen ![]() $k_x$ (Vanneste & Yavneh Reference Vanneste and Yavneh2007; Wang & Balmforth Reference Wang and Balmforth2018). This can be confirmed further by investigating the coincidence of frequency branch crossings with positive growth rates, and is done in Appendix D. This analysis also reveals that as
$k_x$ (Vanneste & Yavneh Reference Vanneste and Yavneh2007; Wang & Balmforth Reference Wang and Balmforth2018). This can be confirmed further by investigating the coincidence of frequency branch crossings with positive growth rates, and is done in Appendix D. This analysis also reveals that as ![]() $k_z$ increases, a different mechanism takes over, with the properties suggesting a CF instability. It is not surprising that a resonance instability has overlap with the CF-type instability, as they can be difficult to distinguish (Leclercq et al. Reference Leclercq, Nguyen and Kerswell2016). Although Park et al. (Reference Park, Billant and Baik2017, Reference Park, Billant, Baik and Seo2018) study TCF, their studies of the competition between CF instability and SRI reveal that one of the main distinguishing features is that the streamwise-dependent CF instability modes are only weakly dependent on the streamwise spatial variable when compared with SRI (meaning they have smaller azimuthal or horizontal wavenumber). This is in good agreement with the classifications we have made here, as the ripples are observed on the larger
$k_z$ increases, a different mechanism takes over, with the properties suggesting a CF instability. It is not surprising that a resonance instability has overlap with the CF-type instability, as they can be difficult to distinguish (Leclercq et al. Reference Leclercq, Nguyen and Kerswell2016). Although Park et al. (Reference Park, Billant and Baik2017, Reference Park, Billant, Baik and Seo2018) study TCF, their studies of the competition between CF instability and SRI reveal that one of the main distinguishing features is that the streamwise-dependent CF instability modes are only weakly dependent on the streamwise spatial variable when compared with SRI (meaning they have smaller azimuthal or horizontal wavenumber). This is in good agreement with the classifications we have made here, as the ripples are observed on the larger ![]() $k_x$ side of the modes that have been identified to be CF type. The growth rates are dominated by the CF-type instability and the ripple effect is only seen where the CF-type instability is weak.
$k_x$ side of the modes that have been identified to be CF type. The growth rates are dominated by the CF-type instability and the ripple effect is only seen where the CF-type instability is weak.
Figure 17(a) displays the eigenfunction of a mode in the lowest ripple of the instability in the ![]() $\varOmega =0.2$ plot of figure 14, and figure 17(b) displays a mode in the fourth ripple from the bottom. The eigenfunction shapes are not similar to those reported above, apart from there does appear to be some localisation towards the left boundary, despite it being fairly weak. The number of oscillations within the region trapped on the left boundary increases as we move up the ripple-type branches, characteristic of resonance instabilities (Le Dizès & Riedinger Reference Le Dizès and Riedinger2010; Park et al. Reference Park, Billant and Baik2017; Wang & Balmforth Reference Wang and Balmforth2018). There are some instabilities related to SRI that are found to be localised at one boundary, such as the RI (Billant & Le Dizès Reference Billant and Le Dizès2009; Le Dizès & Billant Reference Le Dizès and Billant2009; Le Dizès & Riedinger Reference Le Dizès and Riedinger2010; Riedinger et al. Reference Riedinger, Le Dizès and Meunier2011), or due to the presence of baroclinic critical layers (Wang & Balmforth Reference Wang and Balmforth2018), but these mechanisms cause the instability in wavenumber space to become continuous again, which would then not appear as ripples. It is difficult to classify this instability precisely based on the eigenfunctions, but it is likely that it is related to a resonance instability due to the factors discussed previously. Regardless of their origin, the branches are dominated by the CF-type instability in terms of growth rates, and so this is not a region of parameter space where resonance instabilities will dominate.
$\varOmega =0.2$ plot of figure 14, and figure 17(b) displays a mode in the fourth ripple from the bottom. The eigenfunction shapes are not similar to those reported above, apart from there does appear to be some localisation towards the left boundary, despite it being fairly weak. The number of oscillations within the region trapped on the left boundary increases as we move up the ripple-type branches, characteristic of resonance instabilities (Le Dizès & Riedinger Reference Le Dizès and Riedinger2010; Park et al. Reference Park, Billant and Baik2017; Wang & Balmforth Reference Wang and Balmforth2018). There are some instabilities related to SRI that are found to be localised at one boundary, such as the RI (Billant & Le Dizès Reference Billant and Le Dizès2009; Le Dizès & Billant Reference Le Dizès and Billant2009; Le Dizès & Riedinger Reference Le Dizès and Riedinger2010; Riedinger et al. Reference Riedinger, Le Dizès and Meunier2011), or due to the presence of baroclinic critical layers (Wang & Balmforth Reference Wang and Balmforth2018), but these mechanisms cause the instability in wavenumber space to become continuous again, which would then not appear as ripples. It is difficult to classify this instability precisely based on the eigenfunctions, but it is likely that it is related to a resonance instability due to the factors discussed previously. Regardless of their origin, the branches are dominated by the CF-type instability in terms of growth rates, and so this is not a region of parameter space where resonance instabilities will dominate.

Figure 17. Same as figure 16, but with parameters ![]() $\varGamma =0$,
$\varGamma =0$, ![]() $\varOmega =0.2$,
$\varOmega =0.2$, ![]() $N=2$ and
$N=2$ and ![]() ${ {Re}}=50\,000$, along with (a)
${ {Re}}=50\,000$, along with (a) ![]() $k_x=8.3$ and
$k_x=8.3$ and ![]() $k_z=29.5$, and (b)
$k_z=29.5$, and (b) ![]() $k_x=9.4$ and
$k_x=9.4$ and ![]() $k_z=42.2$. The figure shows that the eigenfunctions of instabilities present in the ripples of figure 14 do not provide an easy classification of the type of mode, although the number of oscillations appears to correspond to the different ripples.
$k_z=42.2$. The figure shows that the eigenfunctions of instabilities present in the ripples of figure 14 do not provide an easy classification of the type of mode, although the number of oscillations appears to correspond to the different ripples.
Figure 18 presents a similar analysis of varying rotation rate to figure 14, but now for PCF (![]() $\varGamma =1$). This is done at
$\varGamma =1$). This is done at ![]() ${ {Re}}=5000$ as PCF is more unstable than PPF for arbitrary rotation rate. The non-rotating flow displays only one branch of instability, which was identified by Facchini et al. (Reference Facchini, Favier, Le Gal, Wang and Le Bars2018) as a resonance of IGWs. A non-zero anticyclonic rotation brings with it strong instabilities which persist at all of the tested rotation rates, although it is weaker for larger
${ {Re}}=5000$ as PCF is more unstable than PPF for arbitrary rotation rate. The non-rotating flow displays only one branch of instability, which was identified by Facchini et al. (Reference Facchini, Favier, Le Gal, Wang and Le Bars2018) as a resonance of IGWs. A non-zero anticyclonic rotation brings with it strong instabilities which persist at all of the tested rotation rates, although it is weaker for larger ![]() $\varOmega$ values. These plots are similar to those for PPF presented in figure 14, and so much of the discussion remains valid, although there are some clear differences in that shape of the branch for larger
$\varOmega$ values. These plots are similar to those for PPF presented in figure 14, and so much of the discussion remains valid, although there are some clear differences in that shape of the branch for larger ![]() $\varOmega$, as well as the size of the ripple effect.
$\varOmega$, as well as the size of the ripple effect.

Figure 18. Same as figure 14, but now the flow is PCF (![]() $\varGamma =1$),
$\varGamma =1$), ![]() $N=2$ and
$N=2$ and ![]() ${ {Re}}=5000$. The figure again shows various branches of instability, with the larger branches being stabilised as
${ {Re}}=5000$. The figure again shows various branches of instability, with the larger branches being stabilised as ![]() $\varOmega$ is increased, although they do persist all the way to
$\varOmega$ is increased, although they do persist all the way to ![]() $\varOmega =1$.
$\varOmega =1$.
A gradual increase of the stratification from an unstratified fluid to ![]() $N=2$, in the same way as was done for PPF in figure 15, suggests that the large branch in the
$N=2$, in the same way as was done for PPF in figure 15, suggests that the large branch in the ![]() $\varOmega =0.2$ plot of figure 18 should be classified as a stratification-modified CF instability. Focusing on the eigenfunctions and gradually changing
$\varOmega =0.2$ plot of figure 18 should be classified as a stratification-modified CF instability. Focusing on the eigenfunctions and gradually changing ![]() $\varOmega$ suggests this classification carries through to larger
$\varOmega$ suggests this classification carries through to larger ![]() $\varOmega$ values. Once again, we observe that instability persists beyond the Rayleigh line, and it can be classified as a CF-type modified by stratification.
$\varOmega$ values. Once again, we observe that instability persists beyond the Rayleigh line, and it can be classified as a CF-type modified by stratification.
Beyond ![]() $\varOmega =0.5$, which is the Rayleigh line for PCF, valid for streamwise-independent
$\varOmega =0.5$, which is the Rayleigh line for PCF, valid for streamwise-independent ![]() $k_x=0$ perturbations in an inviscid fluid, the flow appears to still be unstable towards the
$k_x=0$ perturbations in an inviscid fluid, the flow appears to still be unstable towards the ![]() $k_z$-axis. The growth rates in fact decay towards the axis and the flow is stable on it, meaning it satisfies Rayleigh's criterion here and, in fact, the finite
$k_z$-axis. The growth rates in fact decay towards the axis and the flow is stable on it, meaning it satisfies Rayleigh's criterion here and, in fact, the finite ![]() ${ {Re}}$ value causes the instability region to spread closer to that axis.
${ {Re}}$ value causes the instability region to spread closer to that axis.
The ripple effect appears again, but this time with thicker branches, although there are fewer of them. Eigenfunctions of the unstable modes on these branches are presented in figure 19, with figure 19(a) displaying that of a mode in the lowest ripple of the instability in the ![]() $\varOmega =0.2$ plot of figure 18, and figure 19(b) displaying a mode in the next ripple up. Both eigenfunctions resemble the resonance-type SRI modes in the inviscid WKB literature to some extent (Wang & Balmforth Reference Wang and Balmforth2018), with localisation at each boundary, but this localisation is not clear and could be obscured by viscosity. This is most clearly observed through the variable
$\varOmega =0.2$ plot of figure 18, and figure 19(b) displaying a mode in the next ripple up. Both eigenfunctions resemble the resonance-type SRI modes in the inviscid WKB literature to some extent (Wang & Balmforth Reference Wang and Balmforth2018), with localisation at each boundary, but this localisation is not clear and could be obscured by viscosity. This is most clearly observed through the variable ![]() $\hat {v}$ in figure 19(a), with real part showing the component localised at the left boundary and imaginary part showing the localisation at the right boundary. The second of these plots has more oscillations in the region on the left, which is expected as we move up through the ripples. This displays the characteristic features of a resonance-type SRI, although it remains dominated by the stratification modified CF instability.
$\hat {v}$ in figure 19(a), with real part showing the component localised at the left boundary and imaginary part showing the localisation at the right boundary. The second of these plots has more oscillations in the region on the left, which is expected as we move up through the ripples. This displays the characteristic features of a resonance-type SRI, although it remains dominated by the stratification modified CF instability.

Figure 19. Same as figure 16, but with parameters ![]() $\varGamma =1$,
$\varGamma =1$, ![]() $\varOmega =0.2$,
$\varOmega =0.2$, ![]() $N=2$ and
$N=2$ and ![]() ${ {Re}}=5000$, along with (a)
${ {Re}}=5000$, along with (a) ![]() $k_x=3$ and
$k_x=3$ and ![]() $k_z=7.5$ and (b)
$k_z=7.5$ and (b) ![]() $k_x=3$ and
$k_x=3$ and ![]() $k_z=13$. The shown eigenfunctions demonstrate possible resonance between two modes trapped at either side of the domain, although the decay towards the opposite wall is not strong. The number of oscillations again corresponds to different ripples in figure 18.
$k_z=13$. The shown eigenfunctions demonstrate possible resonance between two modes trapped at either side of the domain, although the decay towards the opposite wall is not strong. The number of oscillations again corresponds to different ripples in figure 18.
By gradually increasing the rotation rate from ![]() $\varOmega =0$ to
$\varOmega =0$ to ![]() $\varOmega =0.2$ (not shown here), we can observe that the IGW–IGW resonance instability branch found for
$\varOmega =0.2$ (not shown here), we can observe that the IGW–IGW resonance instability branch found for ![]() $\varOmega =0$, first identified by Facchini et al. (Reference Facchini, Favier, Le Gal, Wang and Le Bars2018), is smoothly connected to the large unstable branch found for
$\varOmega =0$, first identified by Facchini et al. (Reference Facchini, Favier, Le Gal, Wang and Le Bars2018), is smoothly connected to the large unstable branch found for ![]() $\varOmega =0.2$. This branch grows with increasing
$\varOmega =0.2$. This branch grows with increasing ![]() $\varOmega$, and merges with another branch that extends out from
$\varOmega$, and merges with another branch that extends out from ![]() $k_x=0$, to produce what is seen for
$k_x=0$, to produce what is seen for ![]() $\varOmega =0.2$ in figure 18. The same gradual change can be used to track the eigenfunctions, showing how the resonance of two modes localised at each side of the channel gradually changes and becomes more of a global mode with the increase of
$\varOmega =0.2$ in figure 18. The same gradual change can be used to track the eigenfunctions, showing how the resonance of two modes localised at each side of the channel gradually changes and becomes more of a global mode with the increase of ![]() $\varOmega$. This process highlights again the difficulties in distinguishing the origins of the instability branches. However, the largest ripple that extends out from the main branch is clearly seen to develop from the IGW–IGW resonance, supporting the classifications made earlier.
$\varOmega$. This process highlights again the difficulties in distinguishing the origins of the instability branches. However, the largest ripple that extends out from the main branch is clearly seen to develop from the IGW–IGW resonance, supporting the classifications made earlier.
The Reynolds number chosen for ![]() $\varGamma =0$ was 10 times larger than that chosen for
$\varGamma =0$ was 10 times larger than that chosen for ![]() $\varGamma =1$, as the flow appears to stabilise with decreasing
$\varGamma =1$, as the flow appears to stabilise with decreasing ![]() $\varGamma$. Because of this, it is difficult to isolate the effects of changing
$\varGamma$. Because of this, it is difficult to isolate the effects of changing ![]() $\varGamma$. To probe the
$\varGamma$. To probe the ![]() $\varGamma$ dependence, we consider both changing
$\varGamma$ dependence, we consider both changing ![]() $\varGamma$ and changing
$\varGamma$ and changing ![]() ${ {Re}}$ values, noting that we cannot focus on the size of the instability region (as this will be heavily influenced by
${ {Re}}$ values, noting that we cannot focus on the size of the instability region (as this will be heavily influenced by ![]() ${ {Re}}$), but only on the shape of the instability branch and the types of modes that are unstable.
${ {Re}}$), but only on the shape of the instability branch and the types of modes that are unstable.
Figure 20 again shows sequences of growth rate plots, but now for each sequence, the values of ![]() $N$ and
$N$ and ![]() $\varOmega$ are fixed, and we vary both
$\varOmega$ are fixed, and we vary both ![]() $\varGamma$ and
$\varGamma$ and ![]() ${ {Re}}$. The choices of
${ {Re}}$. The choices of ![]() $\varOmega$ values correspond to two cases: one where we expect
$\varOmega$ values correspond to two cases: one where we expect ![]() $k_x=0$ CF instability, and one where we do not.
$k_x=0$ CF instability, and one where we do not.

Figure 20. Growth rate contours for ![]() $N=2$, with
$N=2$, with ![]() $\varOmega =0.2$ (a–e) or
$\varOmega =0.2$ (a–e) or ![]() $\varOmega =0.6$ (f–j). Here
$\varOmega =0.6$ (f–j). Here ![]() $\varGamma$ and
$\varGamma$ and ![]() ${ {Re}}$ are varied as shown in the plot. Each colour bar is valid for the full row of plots, and it has smaller values for (f–j) due to the flow being more stable for the larger
${ {Re}}$ are varied as shown in the plot. Each colour bar is valid for the full row of plots, and it has smaller values for (f–j) due to the flow being more stable for the larger ![]() $\varOmega$ value. The figure demonstrates how the shape of the instability branches is dependent on
$\varOmega$ value. The figure demonstrates how the shape of the instability branches is dependent on ![]() $\varGamma$, although most of the qualitative changes happen for
$\varGamma$, although most of the qualitative changes happen for ![]() $\varGamma >1/2$.
$\varGamma >1/2$.
For both sequences (i.e. both rotation rates), apart from the stabilisation of the Tollmien–Schlichting modes once ![]() $\varGamma =0.25$ is reached, the qualitative picture of the unstable region is unaltered as
$\varGamma =0.25$ is reached, the qualitative picture of the unstable region is unaltered as ![]() $\varGamma$ is increased from zero to
$\varGamma$ is increased from zero to ![]() $\varGamma =0.5$, so we do not expect a change in the instabilities that are supported by the flow. Increasing
$\varGamma =0.5$, so we do not expect a change in the instabilities that are supported by the flow. Increasing ![]() $\varGamma$ further, from
$\varGamma$ further, from ![]() $\varGamma =0.5$ through
$\varGamma =0.5$ through ![]() $\varGamma =0.75$ and to
$\varGamma =0.75$ and to ![]() $\varGamma =1$, we observe changes in each sequence. For the first, shown in the top line of the figure with
$\varGamma =1$, we observe changes in each sequence. For the first, shown in the top line of the figure with ![]() $\varOmega =0.2$, although the main bulk of the unstable region is largely unchanged, we observe that the number of ripple features attached to the right-hand side of the unstable region is reduced. According to our earlier classification, this suggests the number of unique resonances that are unstable is reducing as we move towards PCF (although this number will be influenced by
$\varOmega =0.2$, although the main bulk of the unstable region is largely unchanged, we observe that the number of ripple features attached to the right-hand side of the unstable region is reduced. According to our earlier classification, this suggests the number of unique resonances that are unstable is reducing as we move towards PCF (although this number will be influenced by ![]() ${ {Re}}$). For the second sequence, shown in the bottom row of the figure with
${ {Re}}$). For the second sequence, shown in the bottom row of the figure with ![]() $\varOmega =0.6$, we see a significant change in the shape of the unstable region, becoming more elongated and reaching to larger
$\varOmega =0.6$, we see a significant change in the shape of the unstable region, becoming more elongated and reaching to larger ![]() $k_x$ values. The thin extension part of this region (i.e. the largest
$k_x$ values. The thin extension part of this region (i.e. the largest ![]() $k_x$ values) resembles a single ripple (e.g. in figure 20e), which could suggest the appearance of a resonance instability, according to our earlier classifications. However, it is important to note that apart from the very largest unstable
$k_x$ values) resembles a single ripple (e.g. in figure 20e), which could suggest the appearance of a resonance instability, according to our earlier classifications. However, it is important to note that apart from the very largest unstable ![]() $k_x$ values, this unstable region has fairly significant thickness in
$k_x$ values, this unstable region has fairly significant thickness in ![]() $k_z$ which we would not associate with a resonance, making it difficult to classify (see Appendix D). Eigenfunctions also support the conclusion that no qualitative changes occur between
$k_z$ which we would not associate with a resonance, making it difficult to classify (see Appendix D). Eigenfunctions also support the conclusion that no qualitative changes occur between ![]() $\varGamma =0$ and
$\varGamma =0$ and ![]() $\varGamma =0.5$, being almost identical in that range of
$\varGamma =0.5$, being almost identical in that range of ![]() $\varGamma$ to figure 16(a and c).
$\varGamma$ to figure 16(a and c).
With these observations, we chose ![]() $\varGamma =0.75$ for a more detailed study of a mixed profile. The growth rate spectrum plots are found to be qualitatively similar to those presented in figure 18 for PCF (with some slight variation in the shape), and so they are not presented here. The variation in
$\varGamma =0.75$ for a more detailed study of a mixed profile. The growth rate spectrum plots are found to be qualitatively similar to those presented in figure 18 for PCF (with some slight variation in the shape), and so they are not presented here. The variation in ![]() $\varGamma$ needed to capture all the behaviours can then be reduced to a smaller range by making use of our previous observations.
$\varGamma$ needed to capture all the behaviours can then be reduced to a smaller range by making use of our previous observations.
4.2. Cyclonic rotation ( $\varOmega <0$)
$\varOmega <0$)
Cyclonic rotation is indistinguishable from anticyclonic rotation in the case of the stability of PPF, due to the symmetry of the flow about the channel's midpoint. However, this symmetry is broken for ![]() $\varGamma >0$ and cyclonic flow is found to be much more stable for both
$\varGamma >0$ and cyclonic flow is found to be much more stable for both ![]() $\varGamma =0.75$ and
$\varGamma =0.75$ and ![]() $\varGamma =1$. Up to the largest
$\varGamma =1$. Up to the largest ![]() ${ {Re}}$ tested (
${ {Re}}$ tested (![]() $10^6$), the cyclonic flows for both
$10^6$), the cyclonic flows for both ![]() $\varGamma$ values were stable for
$\varGamma$ values were stable for ![]() $\varOmega \leq -0.4$. Figure 21 displays contour plots of the growth rates over wavenumber space for both
$\varOmega \leq -0.4$. Figure 21 displays contour plots of the growth rates over wavenumber space for both ![]() $\varGamma$ values, calculated at the maximum
$\varGamma$ values, calculated at the maximum ![]() ${ {Re}}$ value of
${ {Re}}$ value of ![]() ${ {Re}}=10^6$, for
${ {Re}}=10^6$, for ![]() $\varOmega =-0.2$. The thin strips suggest resonances play a part in the instability.
$\varOmega =-0.2$. The thin strips suggest resonances play a part in the instability.

Figure 21. Growth rates over wavenumber space for two different values of ![]() $\varGamma$. The constant parameter values here are
$\varGamma$. The constant parameter values here are ![]() $\varOmega =-0.2$,
$\varOmega =-0.2$, ![]() $N=2$ and
$N=2$ and ![]() ${ {Re}}=10^6$.
${ {Re}}=10^6$.
Eigenfunctions, shown in figure 22, support the classification of this instability as resonance-type SRI, as they are a combination of two structures each localised at sides of the domain. The eigenfunctions shown in figure 22(a,c) are on the most unstable branch of ![]() $\varGamma =0.75$ and
$\varGamma =0.75$ and ![]() $\varGamma =1$, respectively, whereas the middle eigenfunction is on the branch that sits slightly higher and to the right of the most unstable one for
$\varGamma =1$, respectively, whereas the middle eigenfunction is on the branch that sits slightly higher and to the right of the most unstable one for ![]() $\varGamma =0.75$, which is why there is more oscillatory behaviour (similar to the observations about figure 19). For cyclonic flow, KWs cannot be part of a resonant pair so resonance-type SRI must be between IGWs, and the more oscillatory branch corresponds to a higher-order IGW (Wang & Balmforth Reference Wang and Balmforth2018).
$\varGamma =0.75$, which is why there is more oscillatory behaviour (similar to the observations about figure 19). For cyclonic flow, KWs cannot be part of a resonant pair so resonance-type SRI must be between IGWs, and the more oscillatory branch corresponds to a higher-order IGW (Wang & Balmforth Reference Wang and Balmforth2018).

Figure 22. Eigenfunctions of the most unstable mode for parameter values ![]() $\varOmega =-0.2$,
$\varOmega =-0.2$, ![]() $N=2$ and
$N=2$ and ![]() ${ {Re}}=10^6$, along with (a)
${ {Re}}=10^6$, along with (a) ![]() $\varGamma =0.75$,
$\varGamma =0.75$, ![]() $k_x=4.4$ and
$k_x=4.4$ and ![]() $k_z=12$, (b)
$k_z=12$, (b) ![]() $\varGamma =0.75$,
$\varGamma =0.75$, ![]() $k_x=4.7$ and
$k_x=4.7$ and ![]() $k_z=15.9$, and (c)
$k_z=15.9$, and (c) ![]() $\varGamma =1$,
$\varGamma =1$, ![]() $k_x=3.6$ and
$k_x=3.6$ and ![]() $k_z=9.65$. The blue lines are the
$k_z=9.65$. The blue lines are the ![]() $\hat {u}$ component of the velocity perturbation and the red lines are the
$\hat {u}$ component of the velocity perturbation and the red lines are the ![]() $\hat {v}$ component, with solid lines showing the real part and dashed lines showing the imaginary part. The eigenfunction shapes aid in the classification of these modes as resonance-type instabilities, as they appear to be two waves localised at the boundaries, with some interaction in the middle region (although the decay towards the opposite boundary is still not strong).
$\hat {v}$ component, with solid lines showing the real part and dashed lines showing the imaginary part. The eigenfunction shapes aid in the classification of these modes as resonance-type instabilities, as they appear to be two waves localised at the boundaries, with some interaction in the middle region (although the decay towards the opposite boundary is still not strong).
Although the introduction of stratification acts to move CF instability above the Rayleigh line at ![]() $\varOmega =0.5$, it does not appear to move the instability below the Rayleigh region and into the cyclonic regime, meaning stratification modified CF instability is not supported by cyclonic rotation. Comparing anticyclonic and cyclonic rotation of the same magnitude, i.e. comparing the
$\varOmega =0.5$, it does not appear to move the instability below the Rayleigh region and into the cyclonic regime, meaning stratification modified CF instability is not supported by cyclonic rotation. Comparing anticyclonic and cyclonic rotation of the same magnitude, i.e. comparing the ![]() $\varOmega =0.2$ plot of figure 18 with the
$\varOmega =0.2$ plot of figure 18 with the ![]() $\varGamma =1$ plot of figure 21, we observe that not only do we need a much larger Reynolds number in order to see instability for cyclonic rotation, but we also find that the growth rates are much smaller. The key conclusion here then is that cyclonic rotation is the only regime where resonance instabilities have the largest growth rates: resonance instabilities are swamped by stratification-modified CF instability for anticyclonic flow.
$\varGamma =1$ plot of figure 21, we observe that not only do we need a much larger Reynolds number in order to see instability for cyclonic rotation, but we also find that the growth rates are much smaller. The key conclusion here then is that cyclonic rotation is the only regime where resonance instabilities have the largest growth rates: resonance instabilities are swamped by stratification-modified CF instability for anticyclonic flow.
4.3. The effects of strong stratification and thermal diffusion
To investigate the flow with stronger stratification, ![]() $N=10$ was chosen. For all three
$N=10$ was chosen. For all three ![]() $\varGamma$ values, the plots showing varying anticyclonic rotation rate are qualitatively similar to those for
$\varGamma$ values, the plots showing varying anticyclonic rotation rate are qualitatively similar to those for ![]() $N=2$, with only a few key differences, and so they are not presented here. First, for PPF, it appears that the Tollmien–Schlichting mode instability branch is not affected by this significant increase in the strength of stratification, and plotting the growth rates in wavenumber space at the same
$N=2$, with only a few key differences, and so they are not presented here. First, for PPF, it appears that the Tollmien–Schlichting mode instability branch is not affected by this significant increase in the strength of stratification, and plotting the growth rates in wavenumber space at the same ![]() ${ {Re}}$ as before (
${ {Re}}$ as before (![]() $50\,000$), reveals that the other instabilities are stabilised and the Tollmien–Schlichting instability is all that remains, meaning it becomes the strongest instability at larger
$50\,000$), reveals that the other instabilities are stabilised and the Tollmien–Schlichting instability is all that remains, meaning it becomes the strongest instability at larger ![]() $N$ values. For both
$N$ values. For both ![]() $\varGamma =0.75$ and
$\varGamma =0.75$ and ![]() $\varGamma =1$, stabilisation due to increased stratification is also observed, and in order to see any instability, a search at higher Reynolds number must be done. Plotting with
$\varGamma =1$, stabilisation due to increased stratification is also observed, and in order to see any instability, a search at higher Reynolds number must be done. Plotting with ![]() $10\times$ the Reynolds number as those for
$10\times$ the Reynolds number as those for ![]() $N=2$ produces qualitatively similar plots. This was expected; although stratification can destabilise the flow, it is also expected that stronger stratification may restabilise the flow (Dubrulle et al. Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005).
$N=2$ produces qualitatively similar plots. This was expected; although stratification can destabilise the flow, it is also expected that stronger stratification may restabilise the flow (Dubrulle et al. Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005).
The plots showing growth rates over wavenumber space for stronger stratification (![]() $N=10$) and cyclonic rotation with strength
$N=10$) and cyclonic rotation with strength ![]() $\varOmega =-0.2$, are shown in figure 23. These plots show some clear differences with figure 21: the branches have slightly different shapes and reach much higher values for both wavenumbers. There are also significantly more branches of instability appearing here. This might have been expected by comparing with a study by Park & Billant (Reference Park and Billant2013), of resonance instabilities in TCF. They find that when the outer cylinder is rotating faster than the inner (which would correspond to a cyclonic flow), the resonance instabilities require strong stratification, and thus as stratification becomes stronger, more of this instability is introduced. Eigenfunctions are not shown again here, but they do show localisation on the two sides of the domain, with a branch that is higher corresponding to more oscillatory behaviour in space, as expected for resonance-type SRI.
$\varOmega =-0.2$, are shown in figure 23. These plots show some clear differences with figure 21: the branches have slightly different shapes and reach much higher values for both wavenumbers. There are also significantly more branches of instability appearing here. This might have been expected by comparing with a study by Park & Billant (Reference Park and Billant2013), of resonance instabilities in TCF. They find that when the outer cylinder is rotating faster than the inner (which would correspond to a cyclonic flow), the resonance instabilities require strong stratification, and thus as stratification becomes stronger, more of this instability is introduced. Eigenfunctions are not shown again here, but they do show localisation on the two sides of the domain, with a branch that is higher corresponding to more oscillatory behaviour in space, as expected for resonance-type SRI.

Figure 23. Same as figure 21, but ![]() $N=10$. The figure suggests that even for stronger stratification, the resonance instabilities are the only ones present in the flow.
$N=10$. The figure suggests that even for stronger stratification, the resonance instabilities are the only ones present in the flow.
Thermal diffusion effects can be added through a finite ![]() ${ {Pr}}$ value, with
${ {Pr}}$ value, with ![]() ${ {Pr}}=7$ chosen here to align with experimental studies of heated fluids (e.g. Gellert & Rüdiger Reference Gellert and Rüdiger2009; Seelig, Harlander & Gellert Reference Seelig, Harlander and Gellert2018; Lopez et al. Reference Lopez, Lopez and Marques2023). The introduction of thermal diffusion only appears to stabilise the flow, reducing the growth rates and the size of the unstable region wavenumbers. The change from
${ {Pr}}=7$ chosen here to align with experimental studies of heated fluids (e.g. Gellert & Rüdiger Reference Gellert and Rüdiger2009; Seelig, Harlander & Gellert Reference Seelig, Harlander and Gellert2018; Lopez et al. Reference Lopez, Lopez and Marques2023). The introduction of thermal diffusion only appears to stabilise the flow, reducing the growth rates and the size of the unstable region wavenumbers. The change from ![]() ${ {Pr}}=\infty$ to
${ {Pr}}=\infty$ to ![]() ${ {Pr}}=7$ is not significant, and instability is still observed in the majority of cases at the same Reynolds number. This was again expected, as Dubrulle et al. (Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005) state that thermal diffusion has a stabilising effect, in their study of stratified and rotating PCF. Stronger diffusion through smaller
${ {Pr}}=7$ is not significant, and instability is still observed in the majority of cases at the same Reynolds number. This was again expected, as Dubrulle et al. (Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005) state that thermal diffusion has a stabilising effect, in their study of stratified and rotating PCF. Stronger diffusion through smaller ![]() ${ {Pr}}$ values could have a more significant effect, but we do not explore that regime here.
${ {Pr}}$ values could have a more significant effect, but we do not explore that regime here.
5. Discussion
A systematic linear stability analysis of rotating plane CPF has been presented in this paper, where the focus was to change both the base flow within the CPF continuum and the rotation rate to see how the Tollmien–Schlichting and CF instability mechanisms compete. In general, the regions of unstable parameter space are the union of those for each mechanism. However, a small extra instability region dominated by 3-D modes is found to exist. We also only found one WKB turning point for the CPF base flow and so no full localisation of the CF modes is possible. When we complexify the base flow so that the shear is non-monotonic in the cross-stream variable, a fully localised CF instability can be found (see Appendix C). While interesting astrophysically, the issue is then, of course, how such a base shear could be set up in the first place.
Adding stable stratification to anticyclonic flow, within the bounds of geophysically relevant ratios of stratification to rotation, introduces resonance instabilities. We argue that they are, however, dominated by a stratification-modified CF instability, which persists beyond the Rayleigh line. Instabilities beyond the Rayleigh line with global eigenfunctions were found by Dubrulle et al. (Reference Dubrulle, Marié, Normand, Richard, Hersant and Zahn2005) and Yavneh et al. (Reference Yavneh, McWilliams and Molemaker2001) in PCF. Both were labelled SRI by the authors, whereas here we find those instabilities to be better interpreted as stratification-modified CF instability. Importantly, this suggests that the instability will exist in a wider range of parameter settings than previously thought. Many studies of stratified and rotating PCF try to avoid CF instability by steering clear of the Rayleigh unstable region which excludes streamwise-independent stratification-modified CF instability. But our calculations show that streamwise-dependent CF modes can be found unstable beyond the Rayleigh line. Adding stratification in the same way to cyclonic flow produces only resonance instabilities. Consequently, resonance instabilities are dominant if and only if the rotation is cyclonic.
An example with CF instability beyond the Rayleigh line can be found in the absence of viscosity, suggesting it is the stratification alone that allows Rayleigh's criterion to be violated. Within the inviscid literature, it is often the case that the horizontal wavenumbers considered are too large to observe the effect, as in Wang & Balmforth (Reference Wang and Balmforth2018). By considering the results they present in figure 4 in presence of viscosity and running over a range of ![]() $k_x$ (reaching smaller values), we can recover both their results (with smaller growth rates) along with the stratification-modified CF instability beyond the Rayleigh line.
$k_x$ (reaching smaller values), we can recover both their results (with smaller growth rates) along with the stratification-modified CF instability beyond the Rayleigh line.
The analysis of a changing CPF reveals that most of the qualitative changes to the instabilities and growth rate spectrums occurs very close to PCF, with almost no changes occurring for ![]() $\varGamma <0.5$. Because of this, further studies can be made more efficient by concentrating on the upper range,
$\varGamma <0.5$. Because of this, further studies can be made more efficient by concentrating on the upper range, ![]() $0.5<\varGamma <1$.
$0.5<\varGamma <1$.
Our results suggest that resonance instabilities are present for both anticyclonic and cyclonic rotation, but cyclonic is the only situation in which resonance instability can be dominate. At this point, it becomes of interest to examine whether the barotropic critical layer itself can generate fresh instability like the baroclinic critical layer (Wang & Balmforth Reference Wang and Balmforth2018). In addition, after the previous discussion about the difference between a resonance-type SRI and a stratification-modified CF instability, it is natural to wonder if this distinction is important for evolution of the flow at later times. We hope to report on the nonlinear simulations of these instabilities in the near future.
Acknowledgements
The authors would like to thank the referees for their comments which have helped to improve the presentation.
Funding
W.O. acknowledges financial support from EPSRC in the form of a studentship.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Exact solutions for inviscid, streamwise-independent instabilities in stratified and rotating PCF
This appendix presents a method to calculate exact solutions for the eigenfunctions under the simplifications that the problem is inviscid and the perturbations are streamwise independent, for PCF. In doing this, we also find an exact expression for the eigenvalues (and, therefore, for the growth rates), which allows us to provide a version of Rayleigh's criterion that has been strengthened to an ‘if and only if’ statement. The criterion is also shown to apply to stably stratified fluids.
The eigenvalue problem given by (2.7)–(2.12) with ![]() $\varGamma =1$ (PCF),
$\varGamma =1$ (PCF), ![]() ${ {Re}} \rightarrow \infty$ (inviscid) and
${ {Re}} \rightarrow \infty$ (inviscid) and ![]() $k_x=0$ (streamwise independent) can be reduced to a second-order ODE in
$k_x=0$ (streamwise independent) can be reduced to a second-order ODE in ![]() $\hat {v}$:
$\hat {v}$:
where ![]() $\sigma$ is a complex eigenvalue, with the growth rate given by
$\sigma$ is a complex eigenvalue, with the growth rate given by ![]() $\mathrm {Re}(\sigma )$ (see (2.6)). This equation has simple solutions, assuming
$\mathrm {Re}(\sigma )$ (see (2.6)). This equation has simple solutions, assuming ![]() $\lambda \neq 0$, written as the sum of complex exponentials:
$\lambda \neq 0$, written as the sum of complex exponentials:
where ![]() $q_+$ and
$q_+$ and ![]() $q_-$ are complex constants. Introduce a new constant
$q_-$ are complex constants. Introduce a new constant ![]() $q$ related to
$q$ related to ![]() $q_+$ through
$q_+$ through ![]() $q_+=q(2\mathrm {i})^{-1}$, and applying boundary conditions (vanishing
$q_+=q(2\mathrm {i})^{-1}$, and applying boundary conditions (vanishing ![]() $\hat {v}$ at
$\hat {v}$ at ![]() $y=0,1$) determines both
$y=0,1$) determines both ![]() $q_-$ and an equation for the eigenvalue
$q_-$ and an equation for the eigenvalue ![]() $\sigma$:
$\sigma$:
Assuming ![]() $q \neq 0$ for non-trivial solutions, this immediately leads to the deduction that
$q \neq 0$ for non-trivial solutions, this immediately leads to the deduction that ![]() $\lambda$ is real, and
$\lambda$ is real, and ![]() $\lambda =n{\rm \pi}$, so that
$\lambda =n{\rm \pi}$, so that ![]() $\sigma$ is quantised through an integer
$\sigma$ is quantised through an integer ![]() $n$:
$n$:
where ![]() $n=0$ is excluded as
$n=0$ is excluded as ![]() $\lambda \neq 0$ was assumed, and only positive
$\lambda \neq 0$ was assumed, and only positive ![]() $n$ needs to be considered. The exact solution for the eigenfunction
$n$ needs to be considered. The exact solution for the eigenfunction ![]() $\hat {v}$ can also be written more clearly as
$\hat {v}$ can also be written more clearly as
where ![]() $q$ can be chosen freely.
$q$ can be chosen freely.
A.1. The stable and unstable regions for unstratified and rotating PCF
First consider the simple case of an unstratified fluid, ![]() $N=0$, which reduces the equation for the eigenvalue to
$N=0$, which reduces the equation for the eigenvalue to
From here, it is possible to immediately deduce a condition for stability, as an unstable solution must have an eigenvalue ![]() $\sigma$ with a positive real part. This means that
$\sigma$ with a positive real part. This means that ![]() $\sigma ^2>0$ is required for instability, as the right-hand side of (A6) is real. That is, there are unstable solutions if and only if
$\sigma ^2>0$ is required for instability, as the right-hand side of (A6) is real. That is, there are unstable solutions if and only if ![]() $2\varOmega (1-2\varOmega )>0$, which equates to
$2\varOmega (1-2\varOmega )>0$, which equates to ![]() $0<\varOmega <1/2$, and gives the same region for stability as Rayleigh's criterion (see § 2.4 and figure 2). However, this is an ‘if and only if’ condition, which is stronger than the original version of Rayleigh's criterion. Provided that the condition for instability is satisfied, there are infinitely many unstable solutions, with eigenvalues indexed by
$0<\varOmega <1/2$, and gives the same region for stability as Rayleigh's criterion (see § 2.4 and figure 2). However, this is an ‘if and only if’ condition, which is stronger than the original version of Rayleigh's criterion. Provided that the condition for instability is satisfied, there are infinitely many unstable solutions, with eigenvalues indexed by ![]() $n$, and growth rates decreasing with increasing
$n$, and growth rates decreasing with increasing ![]() $n$.
$n$.
A.2. The stable and unstable regions for stratified and rotating PCF
When ![]() $N>0$, the region can be found in a similar way. Once again, as the right-hand side of (A4) is real and we require the real part of
$N>0$, the region can be found in a similar way. Once again, as the right-hand side of (A4) is real and we require the real part of ![]() $\sigma$ to be positive for a unstable solution,
$\sigma$ to be positive for a unstable solution, ![]() $\sigma ^2>0$ is required and the numerator in (A4) must be positive:
$\sigma ^2>0$ is required and the numerator in (A4) must be positive:
In order to determine whether the region is stable or unstable, we only need to consider the most unstable mode, i.e. that with the largest growth rate. This is clearly given by the choice ![]() $n=1$, and so we can obtain an instability condition on the rotation rate
$n=1$, and so we can obtain an instability condition on the rotation rate ![]() $\varOmega$:
$\varOmega$:
As ![]() $N$ will be a fixed value, and we can take
$N$ will be a fixed value, and we can take ![]() $k_z$ as large as we like to find an instability, we observe that there are unstable solutions if and only if
$k_z$ as large as we like to find an instability, we observe that there are unstable solutions if and only if ![]() $2\varOmega (1-2\varOmega )>0$. Stratified, rotating, inviscid PCF is unstable to streamwise-independent perturbations if and only if
$2\varOmega (1-2\varOmega )>0$. Stratified, rotating, inviscid PCF is unstable to streamwise-independent perturbations if and only if ![]() $0<\varOmega <1/2$.
$0<\varOmega <1/2$.
Appendix B. Rayleigh's criterion for stratified CPF
This appendix presents a method to find a region in ![]() $\varGamma$–
$\varGamma$–![]() $\varOmega$ space that is stable to streamwise-independent perturbations, assuming the flow is inviscid. A stably stratified version is also included. This is a special case of Rayleigh's well-known criterion, which is valid across our range of base flow profiles determined by
$\varOmega$ space that is stable to streamwise-independent perturbations, assuming the flow is inviscid. A stably stratified version is also included. This is a special case of Rayleigh's well-known criterion, which is valid across our range of base flow profiles determined by ![]() $\varGamma$. It therefore demonstrates that we must relax the assumptions in order to find CF instability beyond the Rayleigh line. More precisely, we must have
$\varGamma$. It therefore demonstrates that we must relax the assumptions in order to find CF instability beyond the Rayleigh line. More precisely, we must have ![]() $k_x\neq 0$.
$k_x\neq 0$.
Consider inviscid flow with streamwise-independent perturbations, governed by (2.7)–(2.12) with ![]() ${ {Re}}\rightarrow \infty$ and
${ {Re}}\rightarrow \infty$ and ![]() $k_x=0$, and eliminate variables in favour of
$k_x=0$, and eliminate variables in favour of ![]() $\hat {v}$:
$\hat {v}$:
subject to ![]() $\hat v = 0$ at
$\hat v = 0$ at ![]() $y=0,1$. Define
$y=0,1$. Define ![]() $\varPhi _\varGamma = 2\varOmega (2\varOmega -U_B')$, where
$\varPhi _\varGamma = 2\varOmega (2\varOmega -U_B')$, where ![]() $\varPhi _\varGamma$ is referred to as the Rayleigh discriminant, and
$\varPhi _\varGamma$ is referred to as the Rayleigh discriminant, and ![]() $U_B' = 1-2(1-\varGamma )y$. Now multiply by the conjugate of
$U_B' = 1-2(1-\varGamma )y$. Now multiply by the conjugate of ![]() $\hat v$ and integrate over the domain
$\hat v$ and integrate over the domain ![]() $[0,1]$:
$[0,1]$:
where integration by parts and boundary conditions simplify some terms. Rearranging gives
where ![]() $K_1^2 \geq 0$ and
$K_1^2 \geq 0$ and ![]() $K_2^2 \geq 0$ can be found precisely by comparing (B2) and (B3). Note from the imaginary part of this equation that
$K_2^2 \geq 0$ can be found precisely by comparing (B2) and (B3). Note from the imaginary part of this equation that ![]() $\sigma ^2$ must be purely real.
$\sigma ^2$ must be purely real.
For now, take ![]() $N=0$, and we require
$N=0$, and we require ![]() $\sigma ^2 \leq 0$ to ensure stability, meaning
$\sigma ^2 \leq 0$ to ensure stability, meaning ![]() $\int _0^1 \varPhi _\varGamma {\left |\hat {v}\right |}^2\, \mathrm {d} y \geq 0$. It is enough to assume
$\int _0^1 \varPhi _\varGamma {\left |\hat {v}\right |}^2\, \mathrm {d} y \geq 0$. It is enough to assume ![]() $\varPhi _\varGamma \geq 0$ for all
$\varPhi _\varGamma \geq 0$ for all ![]() $y$, as then the integrand is always positive, and so is the integral overall; any one of the following must then be satisfied:
$y$, as then the integrand is always positive, and so is the integral overall; any one of the following must then be satisfied:
The conditions in (B4) are therefore sufficient conditions for stability.
The introduction of stratification only acts to weaken the condition required on ![]() $\varPhi _\varGamma$. For general
$\varPhi _\varGamma$. For general ![]() $N$, take the same conditions as those in (B4), then we know they cause
$N$, take the same conditions as those in (B4), then we know they cause ![]() $\int _0^1 \varPhi _\varGamma {\left |\hat {v}\right |}^2\, \mathrm {d} y \geq 0$ to be satisfied, which causes
$\int _0^1 \varPhi _\varGamma {\left |\hat {v}\right |}^2\, \mathrm {d} y \geq 0$ to be satisfied, which causes ![]() $(\int _0^1 \varPhi _\varGamma {\left |\hat {v}\right |}^2\, \mathrm {d} y+N^2K_2^2) \geq 0$. Equation (B3) shows that the conditions in (B4) are sufficient for stability (
$(\int _0^1 \varPhi _\varGamma {\left |\hat {v}\right |}^2\, \mathrm {d} y+N^2K_2^2) \geq 0$. Equation (B3) shows that the conditions in (B4) are sufficient for stability (![]() $\sigma ^2 \leq 0$) provided
$\sigma ^2 \leq 0$) provided ![]() $N^2 \geq 0$ (which is true for stable stratification).
$N^2 \geq 0$ (which is true for stable stratification).
Appendix C. Localised CF instability for a cubic base flow
In this appendix, we demonstrate that localised unstable CF modes are possible for rotating shear flow when the shear is not monotonic in the cross-stream variable ![]() $y$. To illustrate this, we consider simple shear with a cubic part added which vanishes at the walls,
$y$. To illustrate this, we consider simple shear with a cubic part added which vanishes at the walls,
 \begin{equation} U_B(y) = y + \varepsilon\left[\left(\frac{1}{2}-y\right)^3-\frac{1}{4}\left(\frac{1}{2}-y\right)\right]. \end{equation}
\begin{equation} U_B(y) = y + \varepsilon\left[\left(\frac{1}{2}-y\right)^3-\frac{1}{4}\left(\frac{1}{2}-y\right)\right]. \end{equation}
It is worth remarking that ![]() $\varepsilon$ does not have to be very small for the flow profile to look indistinguishable from the constant shear state (see, e.g. figure 24 for
$\varepsilon$ does not have to be very small for the flow profile to look indistinguishable from the constant shear state (see, e.g. figure 24 for ![]() $\varepsilon =0.2$) as
$\varepsilon =0.2$) as
Under the assumption that ![]() $k_z^2 \gg 1$, we can solve (3.1) using the WKB approximation with the WKB turning points (where
$k_z^2 \gg 1$, we can solve (3.1) using the WKB approximation with the WKB turning points (where ![]() $b(y)=0$, see (3.1)) found to be
$b(y)=0$, see (3.1)) found to be
 \begin{equation} y_{{\pm}} = \frac{1}{2}\pm\sqrt{\frac{1}{12}+\frac{1}{3\varepsilon}\left[ (1-2\varOmega)-\frac{\sigma^2}{2\varOmega}\right]}. \end{equation}
\begin{equation} y_{{\pm}} = \frac{1}{2}\pm\sqrt{\frac{1}{12}+\frac{1}{3\varepsilon}\left[ (1-2\varOmega)-\frac{\sigma^2}{2\varOmega}\right]}. \end{equation}
Assuming ![]() $\sigma \simeq \sigma _r$ (guided by numerical solutions), two things are required for localisation. First, both turning points must lie inside the domain and, second, the region trapped by the two turning points must be an oscillatory region, so that
$\sigma \simeq \sigma _r$ (guided by numerical solutions), two things are required for localisation. First, both turning points must lie inside the domain and, second, the region trapped by the two turning points must be an oscillatory region, so that ![]() $b(y)>0$ for
$b(y)>0$ for ![]() $y_{-}< y< y_{+}$. If
$y_{-}< y< y_{+}$. If ![]() $\sigma ^2 \ll 1$, these conditions are simply
$\sigma ^2 \ll 1$, these conditions are simply

Figure 24. The cubic base flow ![]() $U_B(y)$ for
$U_B(y)$ for ![]() $\varepsilon =0.2$ is displayed using a blue line, on top of a simple PCF profile displayed using a black line. The purple line within the inset shows the difference between the cubic base flow and a PCF (i.e.
$\varepsilon =0.2$ is displayed using a blue line, on top of a simple PCF profile displayed using a black line. The purple line within the inset shows the difference between the cubic base flow and a PCF (i.e. ![]() $U_b-y$). This is intended to illustrate how the cubic base flow is almost identical to the PCF for this value of
$U_b-y$). This is intended to illustrate how the cubic base flow is almost identical to the PCF for this value of ![]() $\varepsilon$.
$\varepsilon$.
We now assume ![]() $0<\varOmega <1/2$ (the unstable region for CF modes in PCF), and take
$0<\varOmega <1/2$ (the unstable region for CF modes in PCF), and take ![]() $\varepsilon >0$. The second condition in (C4) is already satisfied, and the first reduces to
$\varepsilon >0$. The second condition in (C4) is already satisfied, and the first reduces to ![]() $2(1-2\varOmega )<\varepsilon$. The WKB method produces a dispersion relation to determine the eigenvalue and a piece-wise solution in the three regions (separated by the two turning points). The usual WKB matching conditions are used at the turning points to write the solution using a single scaling constant
$2(1-2\varOmega )<\varepsilon$. The WKB method produces a dispersion relation to determine the eigenvalue and a piece-wise solution in the three regions (separated by the two turning points). The usual WKB matching conditions are used at the turning points to write the solution using a single scaling constant ![]() $C$. The dispersion relation is
$C$. The dispersion relation is
where ![]() $n$ is a positive integer representing the number of peaks and troughs in the eigenfunction within the oscillatory region, and the WKB eigenfunction is
$n$ is a positive integer representing the number of peaks and troughs in the eigenfunction within the oscillatory region, and the WKB eigenfunction is
 $$\begin{gather}\hat{v}(y) = \frac{C}{[b(y)]^{1/4}}\sin\left(k_z\int_{y_{-}}^{y}\sqrt{b(y')}\, {{\rm d} y}' + \frac{\rm \pi}{4}\right) \quad y_{-}< y< y_{+}, \end{gather}$$
$$\begin{gather}\hat{v}(y) = \frac{C}{[b(y)]^{1/4}}\sin\left(k_z\int_{y_{-}}^{y}\sqrt{b(y')}\, {{\rm d} y}' + \frac{\rm \pi}{4}\right) \quad y_{-}< y< y_{+}, \end{gather}$$ $$\begin{gather}\hat{v}(y) = ({-}1)^{n+1}\frac{C}{2[{-}b(y)]^{1/4}}\exp\left({-}k_z\int_{y_{+}}^{y}\sqrt{-b(y')}\, {{\rm d} y}' \right) \quad y_{+}< y<1. \end{gather}$$
$$\begin{gather}\hat{v}(y) = ({-}1)^{n+1}\frac{C}{2[{-}b(y)]^{1/4}}\exp\left({-}k_z\int_{y_{+}}^{y}\sqrt{-b(y')}\, {{\rm d} y}' \right) \quad y_{+}< y<1. \end{gather}$$ As an example, we take ![]() $\varepsilon =0.2$,
$\varepsilon =0.2$, ![]() $\varOmega =59/120 \approx 0.492$ and
$\varOmega =59/120 \approx 0.492$ and ![]() $k_z=10$. A plot of the base flow for this
$k_z=10$. A plot of the base flow for this ![]() $\varepsilon$ is shown by the blue line in figure 24, superimposed on a black line showing a simple PCF. The governing ODE, given by (3.1), is solved using a shooting algorithm. The initial guess for the eigenvalue is taken from the dispersion relation in (C5), with
$\varepsilon$ is shown by the blue line in figure 24, superimposed on a black line showing a simple PCF. The governing ODE, given by (3.1), is solved using a shooting algorithm. The initial guess for the eigenvalue is taken from the dispersion relation in (C5), with ![]() ${n=5}$, under further simplifying assumptions. Figure 25 displays the numerical eigenfunction, along with the WKB solution plotted using (C6)–(C8). The two show very good qualitative agreement in all regions, provided the
${n=5}$, under further simplifying assumptions. Figure 25 displays the numerical eigenfunction, along with the WKB solution plotted using (C6)–(C8). The two show very good qualitative agreement in all regions, provided the ![]() $y$ value is not too close to the turning points, where the WKB approximation becomes invalid. The numerical eigenvalue is found to be
$y$ value is not too close to the turning points, where the WKB approximation becomes invalid. The numerical eigenvalue is found to be ![]() $\sigma = 0.084499$. The WKB estimate for the eigenvalue is calculated by solving (C5) using a Newton-iteration method along with Simpson's rule for the integral, with the numerical estimate acting as the initial guess for the eigenvalue. This produces
$\sigma = 0.084499$. The WKB estimate for the eigenvalue is calculated by solving (C5) using a Newton-iteration method along with Simpson's rule for the integral, with the numerical estimate acting as the initial guess for the eigenvalue. This produces ![]() $\sigma = 0.084500$, which is in very good agreement with the fully numerical solution.
$\sigma = 0.084500$, which is in very good agreement with the fully numerical solution.

Figure 25. The numerical eigenvector ![]() $\hat {v}$ is displayed using solid lines, with the blue showing the real part and the red showing the imaginary part. The dotted blue lines show the WKB eigenfunction, which is not extended across the turning points as it is not valid there. The dotted line in the left region, middle region and right region are produced using (C6), (C7) and (C8), respectively. The black vertical dashed lines show the location of the WKB turning points. This plot shows the agreement between the numerical and WKB solutions allowing us to deduce that the unstable mode found numerically is in fact fully localised between the two turning points.
$\hat {v}$ is displayed using solid lines, with the blue showing the real part and the red showing the imaginary part. The dotted blue lines show the WKB eigenfunction, which is not extended across the turning points as it is not valid there. The dotted line in the left region, middle region and right region are produced using (C6), (C7) and (C8), respectively. The black vertical dashed lines show the location of the WKB turning points. This plot shows the agreement between the numerical and WKB solutions allowing us to deduce that the unstable mode found numerically is in fact fully localised between the two turning points.
C.1. Small  $\varepsilon$ limit
$\varepsilon$ limit
As ![]() $\varepsilon$ is reduced, the base flow approaches PCF, which is the physically interesting limit. In order to satisfy both
$\varepsilon$ is reduced, the base flow approaches PCF, which is the physically interesting limit. In order to satisfy both ![]() $2(1-2\varOmega )<\varepsilon$ (for the localised instability above) and
$2(1-2\varOmega )<\varepsilon$ (for the localised instability above) and ![]() $\varOmega <1/2$ (as we expect unstable CF modes for this
$\varOmega <1/2$ (as we expect unstable CF modes for this ![]() $\varOmega$ in the PCF limit), we choose
$\varOmega$ in the PCF limit), we choose ![]() $\varOmega$ based on the relation
$\varOmega$ based on the relation ![]() $1-2\varOmega =\lambda \varepsilon /4$, with
$1-2\varOmega =\lambda \varepsilon /4$, with ![]() $0<\lambda <2$. Then, to obtain an approximate expression for
$0<\lambda <2$. Then, to obtain an approximate expression for ![]() $\sigma$, we take
$\sigma$, we take ![]() $\lambda \ll 1$ which leads to
$\lambda \ll 1$ which leads to
 \begin{equation} \sigma=\frac{k_z\sqrt{\varepsilon}}{8\sqrt{3}\left( n-\dfrac{1}{2} \right)} \end{equation}
\begin{equation} \sigma=\frac{k_z\sqrt{\varepsilon}}{8\sqrt{3}\left( n-\dfrac{1}{2} \right)} \end{equation}
assuming that ![]() $\sigma ^2 \ll \varepsilon /4$. A posteriori, this corresponds to the condition
$\sigma ^2 \ll \varepsilon /4$. A posteriori, this corresponds to the condition ![]() $k_z^2 \ll 48(n-\tfrac {1}{2})^2$. This simplified expression makes it clear that there exists localised CF instabilities whose growth rates scale with
$k_z^2 \ll 48(n-\tfrac {1}{2})^2$. This simplified expression makes it clear that there exists localised CF instabilities whose growth rates scale with ![]() $\sqrt {1-2 \varOmega }$ as
$\sqrt {1-2 \varOmega }$ as ![]() $\varOmega \rightarrow \tfrac {1}{2}$ from below. A representative example is the parameter set
$\varOmega \rightarrow \tfrac {1}{2}$ from below. A representative example is the parameter set ![]() $k_z=10$,
$k_z=10$, ![]() $\lambda =0.1$ and
$\lambda =0.1$ and ![]() $n=5$, where the prediction from (C9) is
$n=5$, where the prediction from (C9) is ![]() $0.01604$, the WKB prediction found iteratively from (C5) is
$0.01604$, the WKB prediction found iteratively from (C5) is ![]() $0.015997184$ and the numerical value is
$0.015997184$ and the numerical value is ![]() $0.015997178$, all at
$0.015997178$, all at ![]() $\varepsilon = 10^{-2}$.
$\varepsilon = 10^{-2}$.
Appendix D. Identifying instabilities using frequency branches
In this appendix, we use frequency branches to identify instabilities. The resonance instabilities are attributed to two modes whose frequencies coincide, leading to a positive growth rate, which can therefore be used to classify the instability. Where we cannot see a clear resonance, the instability may be a CF instability, especially if it shares properties with other known examples of such an instability. For some of the instabilities beyond the Rayleigh line, we demonstrate that the frequency branches show clear differences with what is expected for a resonance instability.
First, in figure 26, we examine the ripples in the growth rate contours presented in figure 14(b) (![]() $\varGamma =0$,
$\varGamma =0$, ![]() $\varOmega =0.2$,
$\varOmega =0.2$, ![]() $N=2$,
$N=2$, ![]() ${ {Re}}=50\,000$ and
${ {Re}}=50\,000$ and ![]() ${ {Pr}}=\infty$), by plotting the frequencies and growth rates at
${ {Pr}}=\infty$), by plotting the frequencies and growth rates at ![]() $k_x=9$, for varying
$k_x=9$, for varying ![]() $k_z$. The frequencies coloured red in figure 26(a) correspond to the unstable growth rates seen in figure 26(b). The three thin spikes of instability in the growth rate plot corresponds exactly to what we would expect to see for a resonance instability, based on the literature (see § 1). Looking at the frequencies which correspond to these spikes, we observe points where two frequency branches appear like they should cross smoothly, but appear to interact and move along together horizontally. The correspondence between a growth rate peak and a frequency branch interaction is made clear with a vertical blue dotted line in the figure.
$k_z$. The frequencies coloured red in figure 26(a) correspond to the unstable growth rates seen in figure 26(b). The three thin spikes of instability in the growth rate plot corresponds exactly to what we would expect to see for a resonance instability, based on the literature (see § 1). Looking at the frequencies which correspond to these spikes, we observe points where two frequency branches appear like they should cross smoothly, but appear to interact and move along together horizontally. The correspondence between a growth rate peak and a frequency branch interaction is made clear with a vertical blue dotted line in the figure.

Figure 26. The frequencies shown in (a) are all those that exist within the limits of the plot axes. The unstable frequencies are plotted in red over the top, and they correspond to the unstable growth rates which are also displayed in red in (b). The blue dotted line in each figure shows the same ![]() $k_z$ value, illustrating that a frequency branch crossing matches exactly to a growth rate peak. Parameters are
$k_z$ value, illustrating that a frequency branch crossing matches exactly to a growth rate peak. Parameters are ![]() $k_x=9$,
$k_x=9$, ![]() $\varGamma =0$,
$\varGamma =0$, ![]() $\varOmega =0.2$,
$\varOmega =0.2$, ![]() $N=2$,
$N=2$, ![]() ${ {Re}}=50\,000$ and
${ {Re}}=50\,000$ and ![]() ${ {Pr}}=\infty$. The plot clearly shows the existence of resonance instabilities, which are identified by the spikes of growth rate and frequency branch interactions.
${ {Pr}}=\infty$. The plot clearly shows the existence of resonance instabilities, which are identified by the spikes of growth rate and frequency branch interactions.
Now consider an example in a region where we wish to classify instabilities that have not been identified before. In particular, consider ![]() $\varGamma =0.25$,
$\varGamma =0.25$, ![]() $\varOmega =0.6$,
$\varOmega =0.6$, ![]() $N=2$,
$N=2$, ![]() ${ {Re}} = 40\,000$ and
${ {Re}} = 40\,000$ and ![]() ${ {Pr}}=\infty$. We have a growth rate spectrum for this setting displayed in figure 20(g). The wavenumber
${ {Pr}}=\infty$. We have a growth rate spectrum for this setting displayed in figure 20(g). The wavenumber ![]() $k_x=0.2$ is chosen, and the frequency branches for varying
$k_x=0.2$ is chosen, and the frequency branches for varying ![]() $k_z$, along with the growth rate curves, are shown in figure 27. Although there does appear to be a crossing of frequency branches, this seems to happen with no interaction of the two. This is confirmed by the growth rates shown in figure 27(b), as the branches are clearly not connected. The width of the instability region is also fairly wide in
$k_z$, along with the growth rate curves, are shown in figure 27. Although there does appear to be a crossing of frequency branches, this seems to happen with no interaction of the two. This is confirmed by the growth rates shown in figure 27(b), as the branches are clearly not connected. The width of the instability region is also fairly wide in ![]() $k_z$ space. We can find modes with these properties that are necessarily CF (using
$k_z$ space. We can find modes with these properties that are necessarily CF (using ![]() $N=0$), helping us to classify this as a CF instability rather than a resonance instability.
$N=0$), helping us to classify this as a CF instability rather than a resonance instability.

Figure 27. The frequencies shown in (a) are all those that exist within the limits of the plot axes, and the unstable ones are plotted in red over the top. The growth rates of all the instabilities within this ![]() $k_z$ range are displayed in (b), and again red is used where they become unstable. Parameters are
$k_z$ range are displayed in (b), and again red is used where they become unstable. Parameters are ![]() $k_x=0.2$,
$k_x=0.2$, ![]() $\varGamma =0.25$,
$\varGamma =0.25$, ![]() $\varOmega =0.6$,
$\varOmega =0.6$, ![]() $N=2$,
$N=2$, ![]() ${ {Re}}=40\,000$ and
${ {Re}}=40\,000$ and ![]() ${ {Pr}}=\infty$. This plot shows a mode crossing which appears to be non-interacting, along with a wide band of instability, leading to the conclusion that it is likely of CF origin.
${ {Pr}}=\infty$. This plot shows a mode crossing which appears to be non-interacting, along with a wide band of instability, leading to the conclusion that it is likely of CF origin.
Further to this, consider an example where the base flow is at the other limit of ![]() $\varGamma =1$ (PCF). For
$\varGamma =1$ (PCF). For ![]() $\varOmega =0.6$,
$\varOmega =0.6$, ![]() $N=2$,
$N=2$, ![]() ${ {Re}}=5\,000$ and
${ {Re}}=5\,000$ and ![]() ${ {Pr}}=\infty$, we have a growth rate spectrum displayed in both figure 20(j) and figure 18(d). Choosing
${ {Pr}}=\infty$, we have a growth rate spectrum displayed in both figure 20(j) and figure 18(d). Choosing ![]() $k_x=0.4$ puts us in a regime where we have instability for a wide range of
$k_x=0.4$ puts us in a regime where we have instability for a wide range of ![]() $k_z$. We plot the frequency branches and growth rates for this case in figure 28(a,c). This plot shows an important difference with what is expected from a resonance, by comparing to figure 26 and the literature. In particular, the horizontal extent (more precisely, its width relative to the size of
$k_z$. We plot the frequency branches and growth rates for this case in figure 28(a,c). This plot shows an important difference with what is expected from a resonance, by comparing to figure 26 and the literature. In particular, the horizontal extent (more precisely, its width relative to the size of ![]() $k_z$) of the red line of instability joining the two blue branches is beyond what would be expected, as resonance instabilities should be thin regions in
$k_z$) of the red line of instability joining the two blue branches is beyond what would be expected, as resonance instabilities should be thin regions in ![]() $k_z$ space. Further to this, the size of this feature in
$k_z$ space. Further to this, the size of this feature in ![]() $k_z$ space persists for larger Reynolds numbers (
$k_z$ space persists for larger Reynolds numbers (![]() ${ {Re}} = 40\,000$), displayed in the second column of the figure, suggesting this is not just a finite viscosity effect. We therefore cannot use this method to classify these types of modes as resonance instabilities.
${ {Re}} = 40\,000$), displayed in the second column of the figure, suggesting this is not just a finite viscosity effect. We therefore cannot use this method to classify these types of modes as resonance instabilities.

Figure 28. The frequencies shown in (a,b) are all those that exist within the limits of the plot axes for the specified Reynolds number (shown in the plot), and the frequencies associated with positive growth rates are plotted in red over the top. There are some branches plotted in blue which correspond to the blue growth rate curves on (c,d). The other parameters are ![]() $k_x=0.4$,
$k_x=0.4$, ![]() $\varGamma =1$,
$\varGamma =1$, ![]() $\varOmega =0.6$,
$\varOmega =0.6$, ![]() $N=2$ and
$N=2$ and ![]() ${ {Pr}}=\infty$. This plot demonstrates the extent in
${ {Pr}}=\infty$. This plot demonstrates the extent in ![]() $k_z$ space of the unstable feature, which persists for larger Reynolds numbers, making it difficult to classify.
$k_z$ space of the unstable feature, which persists for larger Reynolds numbers, making it difficult to classify.