Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-19T09:10:30.129Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixed convection in turbulent channels with unstable stratification

Published online by Cambridge University Press:  25 May 2017

Sergio Pirozzoli Open the ORCID record for Sergio Pirozzoli [Opens in a new window] ,
Matteo Bernardini ,
Roberto Verzicco Open the ORCID record for Roberto Verzicco [Opens in a new window]  and
Paolo Orlandi
Sergio Pirozzoli*
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza Università di Roma, Via Eudossiana 18, 00184 Roma, Italy
Matteo Bernardini
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza Università di Roma, Via Eudossiana 18, 00184 Roma, Italy
Roberto Verzicco
Affiliation:
Dipartimento di Ingegneria Industriale, Università di Roma Tor Vergata, 00133 Roma, Italy Physics of Fluids Group, University of Twente, 7500 AE Enschede, The Netherlands
Paolo Orlandi
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza Università di Roma, Via Eudossiana 18, 00184 Roma, Italy
*
†Email address for correspondence: sergio.pirozzoli@uniroma1.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We study turbulent flows in pressure-driven planar channels with imposed unstable thermal stratification, using direct numerical simulations in a wide range of Reynolds and Rayleigh numbers and reaching flow conditions which are representative of fully developed turbulence. The combined effect of forced and free convection produces a peculiar pattern of quasi-streamwise rollers occupying the full channel thickness, with aspect ratio considerably higher than unity; it has been observed that they have an important redistributing effect on temperature and momentum, providing for a substantial fraction of the heat and momentum flux at bulk Richardson numbers larger than $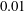0.01$. The mean values and the variances of the flow variables do not appear to follow Prandtl’s scaling in the free-convection regime, except for the temperature and vertical velocity fluctuations, which are more directly affected by wall-attached turbulent plumes. We find that the Monin–Obukhov theory nevertheless yields a useful representation of the main flow features. In particular, the widely used Businger–Dyer flux-profile relationships are found to provide a convenient way of approximately accounting for the bulk effects of friction and buoyancy, although the individual profiles may have wide scatter from the alleged trends. Significant deviations are found in direct numerical simulations with respect to the commonly used parametrization of the momentum flux in the light-wind regime, which may have important practical impact in wall models of atmospheric dynamics. Finally, for modelling purposes, we devise a set of empirical predictive formulae for the heat flux and friction coefficients, which are within approximately 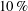$10\,\%$ standard deviation from the numerical results in a wide range of flow parameters.

JFM classification

Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 821 , 25 June 2017 , pp. 482 - 516
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H. & Antonia, R. A. 2009 Near-wall similarity between velocity and scalar fluctuations in a turbulent channel flow. Phys. Fluids 21, 025109.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.Google Scholar
Ahlers, G., He, X., Funfschilling, D. & Bodenschatz, E. 2012 Heat transport by turbulent Rayleigh–Bénard convection for Pr ≃ 0. 8 and 3 × 1012⩽Ra⩽1015 : aspect ratio 𝛾 = 0. 50. New J. Phys. 14, 103012.Google Scholar
Armenio, V. & Sarkar, S. 2002 An investigation of stably stratified turbulent channel flow using large-eddy simulation. J. Fluid Mech. 459, 1–42.Google Scholar
Avsec, D. 1937 Sur les formes ondulées des tourbillons en bandes longitudinales. C. R. Acad. Sci. Paris 204, 167–169.Google Scholar
Avsec, D. & Luntz, M. 1937 Tourbillons thermoconvectifs et électroconvectifs. La Météorologie 31, 180–194.Google Scholar
Bénard, H. & Avsec, D. 1938 Travaux récents sur les tourbillons cellulaires et les tourbillons en bandes. Applications à l’astrophysique et à la météorologie. J. Phys. Radium 9 (11), 486–500.Google Scholar
Bergman, T. L., Lavine, A. S., Incropera, F. P. & DeWitt, D. P. 2011 Introduction to Heat Transfer. Wiley.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 742, 171–191.Google Scholar
Brown, R. A. 1980 Longitudinal instabilities and secondary flows in the planetary boundary layer: a review. Rev. Geophys. 18 (3), 683–697.CrossRefGoogle Scholar
Businger, J. A., Wyngaard, J. C., Izumi, Y. & Bradley, E. F. 1971 Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 28 (2), 181–189.2.0.CO;2>CrossRefGoogle Scholar
Cebeci, T. & Bradshaw, P. 1984 Physical and Computational Aspects of Convective Heat Transfer. Springer.Google Scholar
Chung, D. & Matheou, G. 2012 Direct numerical simulation of stationary homogeneous stratified sheared turbulence. J. Fluid Mech. 696, 434–467.CrossRefGoogle Scholar
Clever, R. M. & Busse, F. H. 1991 Instabilities of longitudinal rolls in the presence of Poiseuille flow. J. Fluid Mech. 229, 517–529.Google Scholar
Clever, R. M. & Busse, F. H. 1992 Three-dimensional convection in a horizontal fluid layer subjected to a constant shear. J. Fluid Mech. 234, 511–527.Google Scholar
Deardorff, J. W. 1970 Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection. J. Atmos. Sci. 27 (8), 1211–1213.2.0.CO;2>CrossRefGoogle Scholar
Deardorff, J. W. 1972 Numerical investigation of neutral and unstable planetary boundary layers. J. Atmos. Sci. 29 (1), 91–115.Google Scholar
Domaradzki, J. A. & Metcalfe, R. W. 1988 Direct numerical simulations of the effects of shear on turbulent Rayleigh–Bénard convection. J. Fluid Mech. 193, 499–531.Google Scholar
Dyer, A. J. 1974 A review of flux-profile relationships. Boundary-Layer Meteorol. 7 (3), 363–372.Google Scholar
Esau, I., Davy, R., Outten, S., Tyuryakov, S. & Zilitinkevich, S. 2013 Structuring of turbulence and its impact on basic features of Ekman boundary layers. Nonlinear Process. Geophys. 20, 589–604.Google Scholar
Fukui, K. & Nakajima, M. 1985 Unstable stratification effects on turbulent shear flow in the wall region. Intl J. Heat Mass Transfer 28 (12), 2343–2352.Google Scholar
Fukui, K., Nakajima, M. & Ueda, H. 1991 Coherent structure of turbulent longitudinal vortices in unstably-stratified turbulent flow. Intl J. Heat Mass Transfer 34 (9), 2373–2385.Google Scholar
Gage, K. S. & Reid, W. H. 1968 The stability of thermally stratified plane Poiseuille flow. J. Fluid Mech. 33 (01), 21–32.Google Scholar
Garai, A., Kleissl, J. & Sarkar, S. 2014 Flow and heat transfer in convectively unstable turbulent channel flow with solid-wall heat conduction. J. Fluid Mech. 757, 57–81.Google Scholar
Garcia-Villalba, M. & del Álamo, J. C. 2011 Turbulence modification by stable stratification in channel flow. Phys. Fluids 23 (4), 045104.Google Scholar
Haines, D. A. 1982 Horizontal roll vortices and crown fires. J. Appl. Meteorol. 21 (6), 751–763.Google Scholar
Hamman, C. & Moin, P. 2015 Thermal convection from a minimal flow unit to a wide fluid layer. Bull. Am. Phys. Soc. 60 (21). See http://meetings.aps.org/link/BAPS.2015.DFD.L11.8.Google Scholar
Hanna, S. R. 1969 The formation of longitudinal sand dunes by large helical eddies in the atmosphere. J. Appl. Meteorol. 8 (6), 874–883.Google Scholar
Hill, G. E. 1968 On the orientation of cloud bands. Tellus 20 (1), 132–137.CrossRefGoogle Scholar
Iida, O. & Kasagi, N. 1997 Direct numerical simulation of unstably stratified turbulent channel flow. Trans. ASME J. Heat Transfer 119 (1), 53–61.Google Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
Johansson, C., Smedman, A.-S., Högström, U., Brasseur, J. G. & Khanna, S. 2001 Critical test of the validity of Monin–Obukhov similarity during convective conditions. J. Atmos. Sci. 58 (12), 1549–1566.2.0.CO;2>CrossRefGoogle Scholar
Kader, B. A. 1981 Temperature and concentration profiles in fully turbulent boundary layers. Intl J. Heat Mass Transfer 24, 1541–1544.Google Scholar
Kader, B. A. & Yaglom, A. M. 1990 Mean fields and fluctuation moments in unstably stratified turbulent boundary layers. J. Fluid Mech. 212, 637–662.Google Scholar
Katul, G. G., Li, D., Chamecki, M. & Bou-Zeid, E. 2013 Mean scalar concentration profile in a sheared and thermally stratified atmospheric surface layer. Phys. Rev. E 87 (2), 023004.Google Scholar
Kays, W. M., Crawford, M. E. & Weigand, B. 1980 Convective Heat and Mass Transfer. McGraw-Hill.Google Scholar
Kerr, R. M. 1996 Rayleigh number scaling in numerical convection. J. Fluid Mech. 310, 139–179.Google Scholar
Khanna, S. & Brasseur, J. G. 1997 Analysis of Monin–Obukhov similarity from large-eddy simulation. J. Fluid Mech. 345, 251–286.Google Scholar
Khanna, S. & Brasseur, J. G. 1998 Three-dimensional buoyancy-and shear-induced local structure of the atmospheric boundary layer. J. Atmos. Sci. 55 (5), 710–743.Google Scholar
Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kuettner, J. P. 1959 The band structure of the atmosphere. Tellus 11 (3), 267–294.Google Scholar
Kuettner, J. P. 1971 Cloud bands in the earth’s atmosphere: observations and theory. Tellus 23 (4–5), 404–426.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct simulation of turbulent channel flow layer up to Re 𝜏 = 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Li, D. & Bou-Zeid, E. 2011 Coherent structures and the dissimilarity of turbulent transport of momentum and scalars in the unstable atmospheric surface layer. Boundary-Layer Meteorol. 140 (2), 243–262.Google Scholar
Mal, S. 1930 Forms of stratified clouds. Beitr. Phys. Atmos. 17, 40–68.Google Scholar
Mizushina, T., Ogino, F. & Katada, N. 1982 Ordered motion of turbulence in a thermally stratified flow under unstable conditions. Intl J. Heat Mass Transfer 25 (9), 1419–1425.Google Scholar
Monin, A. S. & Obukhov, A. M. 1954 Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 151, 163–187.Google Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.Google ScholarPubMed
Obukhov, A. M. 1946 Turbulence in an atmosphere with inhomogeneous temperature. Trudy Geofiz. Inst. AN SSSR 1, 95–115.Google Scholar
Orlandi, P., Bernardini, M. & Pirozzoli, S. 2015a Poiseuille and Couette flows in the transitional and fully turbulent regime. J. Fluid Mech. 770, 424–441.Google Scholar
Orlandi, P., Pirozzoli, S. & Bernardini, M. 2015b Influence of wall roughness and thermal coductivity on turbulent natural convection. Bull. Am. Phys. Soc. 60 (21). See http://meetings.aps.org/link/BAPS.2015.DFD.A20.3.Google Scholar
Pabiou, H., Mergui, S. & Benard, C. 2005 Wavy secondary instability of longitudinal rolls in Rayleigh–Bénard–Poiseuille flows. J. Fluid Mech. 542, 175–194.Google Scholar
Panofsky, H. A., Tennekes, H., Lenschow, D. H. & Wyngaard, J. C. 1977 The characteristics of turbulent velocity components in the surface layer under convective conditions. Boundary-Layer Meteorol. 11 (3), 355–361.Google Scholar
Papavassiliou, D. V. & Hanratty, T. J. 1997 Interpretation of large-scale structures observed in a turbulent planet Couette flow. Intl J. Heat Fluid Flow 18, 55–69.Google Scholar
Park, S.-B. & Baik, J.-J. 2014 Large-eddy simulations of convective boundary layers over flat and urbanlike surfaces. J. Atmos. Sci. 71, 1880–1892.Google Scholar
Patton, E. G., Sullivan, P. P., Shaw, R. H., Finnigan, J. J. & Weil, J. C. 2014 Atmospheric stability influences on coupled boundary layer and canopy turbulence. J. Atmos. Sci. 73, 1621–1647.Google Scholar
Paulson, C. A. 1970 The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer. J. Appl. Meteorol. 9 (6), 857–861.Google Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2014 Turbulence statistics in Couette flow at high Reynolds number. J. Fluid Mech. 758, 327–343.Google Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2016 Passive scalars in turbulent channel flow at high Reynolds number. J. Fluid Mech. 788, 614–639.Google Scholar
Prandtl, L. 1932 Meteorologische anwendung der strömungslehre. Beitr. Phys. Atmos. 19, 188–202.Google Scholar
Rao, K. G. 2004 Estimation of the exchange coefficient of heat during low wind convective conditions. Boundary-Layer Meteorol. 111 (2), 247–273.Google Scholar
Rao, K. G. & Narasimha, R. 2006 Heat-flux scaling for weakly forced turbulent convection in the atmosphere. J. Fluid Mech. 547, 115–135.Google Scholar
Scagliarini, A., Einarsson, H., Gylfason, Á. & Toschi, F. 2015 Law of the wall in an unstably stratified turbulent channel flow. J. Fluid Mech. 781, R5.Google Scholar
Scagliarini, A., Gylfason, Á. & Toschi, F. 2014 Heat-flux scaling in turbulent Rayleigh–Bénard convection with an imposed longitudinal wind. Phys. Rev. E 89 (4), 043012.Google Scholar
Shah, S. K. & Bou-Zeid, E. 2014 Direct numerical simulations of turbulent Ekman layers with increasing static stability: modifications to the bulk structure and second-order statistics. J. Fluid Mech. 760, 494–539.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.Google Scholar
Sid, S., Dubief, Y. & Terrapon, V. 2015 Direct numerical simulation of mixed convection in turbulent channel flow: on the Reynolds number dependency of momentum and heat transfer under unstable stratification. In Proceedings of the 8th International Conference on Computational Heat and Mass Transfer, Istanbul, Turkey, p. 190.Google Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.Google Scholar
Stull, R. B. 2012 An Introduction to Boundary Layer Meteorology, vol. 13. Springer Science & Business Media.Google Scholar
Wyngaard, J. C. 1992 Atmospheric turbulence. Annu. Rev. Fluid Mech. 24 (1), 205–234.Google Scholar
Wyngaard, J. C., Coté, O. R. & Izumi, Y. 1971 Local free convection, similarity, and the budgets of shear stress and heat flux. J. Atmos. Sci. 28 (7), 1171–1182.Google Scholar
Young, G. S., Kristovich, D. A. R., Hjelmfelt, M. R. & Foster, R. C. 2002 Rolls, streets, waves, and more: a review of quasi-two-dimensional structures in the atmospheric boundary layer. Bull. Am. Meteorol. Soc. 83 (7), 997–1001.Google Scholar
Zilitinkevich, S. J., Hunt, J. C. R., Esau, I. N., Grachev, A. A., Lalas, D. P., Akylas, E., Tombrou, M., Fairall, C. W., Fernando, H. J. S., Baklanov, A. A. et al. 2006 The influence of large convective eddies on the surface-layer turbulence. Q. J. R. Meteorol. Soc. 132, 1426–1456.Google Scholar
Zonta, F. & Soldati, A. 2014 Effect of temperature dependent fluid properties on heat transfer in turbulent mixed convection. Trans. ASME J. Heat Transfer 136 (2), 022501.Google Scholar