Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-27T10:42:23.053Z Has data issue: false hasContentIssue false
  • English
  • Français

Mode competition in galloping of a square cylinder at low Reynolds number

Published online by Cambridge University Press:  27 March 2019

Xintao Li ,
Zhen Lyu ,
Jiaqing Kou  and
Weiwei Zhang Open the ORCID record for Weiwei Zhang [Opens in a new window]
Xintao Li
Affiliation:
School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
Zhen Lyu
Affiliation:
School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
Jiaqing Kou
Affiliation:
School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
Weiwei Zhang*
Affiliation:
School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
*
†Email address for correspondence: aeroelastic@nwpu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Galloping is a type of fluid-elastic instability phenomenon characterized by large-amplitude low-frequency oscillations of the structure. The aim of the present study is to reveal the underlying mechanisms of galloping of a square cylinder at low Reynolds numbers (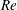$Re$) via linear stability analysis (LSA) and direct numerical simulations. The LSA model is constructed by coupling a reduced-order fluid model with the structure motion equation. The relevant unstable modes are first yielded by LSA, and then the development and evolution of these modes are investigated using direct numerical simulations. 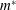It is found that, for certain combinations of $Re$ and mass ratio ($m^{\ast }$), the structure mode (SM) becomes unstable beyond a critical reduced velocity 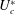$U_{c}^{\ast }$ due to the fluid–structure coupling effect. The galloping oscillation frequency matches exactly the eigenfrequency of the SM, suggesting that the instability of the SM is the primary cause of galloping phenomenon. Nevertheless, the 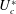$U_{c}^{\ast }$ predicted by LSA is significantly lower than the galloping onset 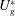$U_{g}^{\ast }$ obtained from numerical simulations. Further analysis indicates that the discrepancy is caused by the nonlinear competition between the leading fluid mode (FM) and the SM. In the pre-galloping region 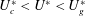$U_{c}^{\ast }<U^{\ast }<U_{g}^{\ast }$, the FM quickly reaches the nonlinear saturation state and then inhibits the development of the SM, thus postponing the occurrence of galloping. When 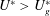$U^{\ast }>U_{g}^{\ast }$, mode competition is weakened because of the large difference in mode frequencies, and thereby no mode lock-in can happen. Consequently, galloping occurs, with the responses determined by the joint action of SM and FM. The unstable SM leads to the low-frequency large-amplitude vibration of the cylinder, while the unstable FM results in the high-frequency vortex shedding in the wake. The dynamic mode decomposition (DMD) technique is successfully applied to extract the coherent flow structures corresponding to SM and FM, which we refer to as the galloping mode and the von Kármán mode, respectively. In addition, we show that, due to the mode competition mechanism, the galloping-type oscillation completely disappears below a critical mass ratio. From these results, we conclude that transverse galloping of a square cylinder at low 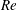$Re$ is essentially a kind of single-degree-of-freedom (SDOF) flutter, superimposed by a forced vibration induced by the natural vortex shedding. Mode competition between SM and FM in the nonlinear stage can put off the onset of galloping, and can completely suppress the galloping phenomenon at relatively low 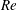$Re$ and low 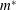$m^{\ast }$ conditions.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 516 - 555
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75, 750–756.Google Scholar
Barrero-Gil, A., Sanz-Andrés, A. & Roura, M. 2009 Transverse galloping at low Reynolds numbers. J. Fluids Struct. 25, 1236–1242.Google Scholar
Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27 (5), 648–658.Google Scholar
Bearman, P. W., Gartshore, I. S., Maull, D. & Parkinson, G. V. 1987 Experiments on flow-induced vibration of a square-section cylinder. J. Fluids Struct. 1, 19–34.Google Scholar
Bearman, P. W. & Luo, S. C. 1988 Investigation of the aerodynamic instability of a square-section cylinder by forced oscillation. J. Fluids Struct. 2, 161–176.Google Scholar
Bearman, P. W. & Obasaju, E. D. 1982 An experimental study of pressure fluctuations on fixed and oscillating square-section cylinders. J. Fluid Mech. 119, 297–321.Google Scholar
Billah, K. Y. & Scanlan, R. H. 1991 Resonance, Tacoma Narrows bridge failure, and undergraduate physics textbooks. Am. J. Phys. 59, 118–124.Google Scholar
Bishop, R. E. D. & Hassan, A. Y. 1964 The lift and drag forces on a circular cylinder oscillating in a flowing fluid. Proc. R. Soc. Lond. A 277, 51–75.Google Scholar
Blevins, R. D. 1990 Flow-induced Vibration. Van Nostrand Reinhold.Google Scholar
Bokaian, A. & Geoola, F. 1985 Effects of vortex-resonance on nearby galloping instability. J. Engng Mech. 111, 591–609.Google Scholar
Bouclin, D. N.1977 Hydroelastic oscillations of square cylinders. Master’s thesis, University of British Columbia, Vancouver, BC, Canada.Google Scholar
Bourguet, R. & Jacono, D. L. 2014 Flow-induced vibrations of a rotating cylinder. J. Fluid Mech. 740, 342–380.Google Scholar
Box, G., Jenkins, G. M. & Reinsel, G. C. 1994 Time Series Analysis: Forecasting and Control. Prentice-Hall.Google Scholar
Corless, R. M. & Parkinson, G. V. 1988 A model of the combined effects of vortex-induced oscillation and galloping. J. Fluids Struct. 2, 203–220.Google Scholar
Corless, R. M. & Parkinson, G. V. 1993 Mathematical modelling of the combined effects of vortex-induced vibration and galloping. Part II. J. Fluids Struct. 7, 825–848.Google Scholar
Cossu, C. & Morino, L. 2000 On the instability of a spring-mounted circular cylinder in a viscous flow at low Reynolds numbers. J. Fluids Struct. 14 (2), 183–196.Google Scholar
Cui, Z., Zhao, M., Teng, B. & Cheng, L. 2015 Two-dimensional numerical study of vortex-induced vibration and galloping of square and rectangular cylinders in steady flow. Ocean Engng 106, 189–206.Google Scholar
De Boer, A., Van der Schoot, M. S. & Bijl, H. 2007 Mesh deformation based on radial basis function interpolation. Comput. Struct. 85, 784–795.Google Scholar
Den Hartog, J. P. 1932 Transmission line vibration due to sleet. Trans. Amer. Inst. Electrical Engineers 51, 1074–1076.Google Scholar
Dimitriadis, G. 2017 Introduction to Nonlinear Aeroelasticity. Wiley.Google Scholar
Dowell, E. H. 1980 A Modern Course in Aeroelasticity. Springer.Google Scholar
Feng, C. C.1968 The measurement of vortex induced effects in flow past stationary and oscillating circular and d-section cylinders. Masters thesis, University of British Columbia, Vancouver, BC, Canada.Google Scholar
Gao, C., Zhang, W., Li, X., Liu, Y., Quan, J., Ye, Z. & Jiang, Y. 2017 Mechanism of frequency lock-in in transonic buffeting flow. J. Fluid Mech. 818, 528–561.Google Scholar
Gao, C., Zhang, W. & Ye, Z. 2016 A new viewpoint on the mechanism of transonic single-degree-of-freedom flutter. Aerosp. Sci. Technol. 52, 144–156.Google Scholar
Gao, G. & Zhu, L. 2017 Nonlinear mathematical model of unsteady galloping force on a rectangular 2 : 1 cylinder. J. Fluids Struct. 70, 47–71.Google Scholar
Ghoreyshi, M., Jirasek, A. & Cummings, R. M. 2014 Reduced-order unsteady aerodynamics modeling for stability and control analysis using computational fluid dynamics. Prog. Aerosp. Sci. 71, 167–217.Google Scholar
Hartlen, R. T. & Currie, I. G. 1970 Lift-oscillator model of vortex-induced vibration. J. Engng Mech. Div. 96, 577–591.Google Scholar
Jaiman, R. K., Guan, M. Z. & Miyanawala, T. P. 2016 Partitioned iterative and dynamic subgrid-scale methods for freely vibrating square-section structures at subcritical Reynolds number. Comput. Struct. 133, 68–89.Google Scholar
Jaiman, R. K., Sen, S. & Gurugubelli, P. S. 2015 A fully implicit combined field scheme for freely vibrating square cylinders with sharp and rounded corners. Comput. Struct. 70, 47–71.Google Scholar
Joly, A., Etienne, S. & Pelletier, D. 2012 Galloping of square cylinders in cross-flow at low Reynolds numbers. J. Fluids Struct. 28, 232–243.Google Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13, 7–8.Google Scholar
Kou, J. & Zhang, W. 2017 An improved criterion to select dominant modes from dynamic mode decomposition. Eur. J. Mech. 62, 109–129.Google Scholar
Kou, J. & Zhang, W. 2019 A hybrid reduced-order framework for complex aeroelastic simulations. Aerosp. Sci. Technol. 84, 880–894.Google Scholar
de Langre, E. 2006 Frequency lock-in is caused by coupled-mode flutter. J. Fluids Struct. 22 (6), 783–791.Google Scholar
Li, X., Zhang, W. & Gao, C. 2018 Proximity-interference wake-induced vibration at subcritical Re: mechanism analysis using a linear dynamic model. Phys. Fluids 30, 033606.Google Scholar
Liou, M. S. 2006 A sequel to ausm, part II: ausm+-up for all speeds. J. Comput. Phys. 214, 137–170.Google Scholar
Lucia, D. J., Beran, P. S. & Silva, W. A. 2004 Reduced-order modeling: new approaches for computational physics. Prog. Aerosp. Sci. 40, 51–117.Google Scholar
Mannini, C., Marra, A. M. & Bartoli, G. 2014 VIV-galloping instability of rectangular cylinders: review and new experiments. J. Wind Engng Ind. Aerodyn. 132, 109–124.Google Scholar
Mannini, C., Marra, A. M. & Bartoli, G. 2015 Experimental investigation on VIV-galloping interaction of a rectangular 3 : 2 cylinder. Meccanica 50, 841–853.Google Scholar
Mannini, C., Marra, A. M. & Bartoli, G. 2016 Interference of vortex-induced vibration and transverse galloping for a rectangular cylinder. J. Fluids Struct. 66, 403–423.Google Scholar
Mannini, C., Massai, T. & Marra, A. M. 2018 Modeling the interference of vortex-induced vibration and galloping for a slender rectangular prism. J. Sound Vib. 439, 493–509.Google Scholar
McNamara, J. J. & Friedmann, P. P. 2007 Flutter-boundary identification for time-domain computational aeroelasticity. AIAA J. 45, 1546–1555.Google Scholar
Meliga, P. & Chomaz, J. M. 2011 An asymptotic expansion for the vortex-induced vibrations of a circular cylinder. J. Fluid Mech. 671, 137–167.Google Scholar
Nakamura, Y. 1969 Vortex excitation of a circular cylinder treated as a binary flutter. Rep. Res. Inst. Appl. Mech. 17, 217–234.Google Scholar
Nakamura, Y. 1990 Recent research into bluff-body flutter. J. Wind Engng Ind. Aerodyn. 33, 1–10.Google Scholar
Nakamura, Y. & Matsukawa, T. 1987 Vortex excitation of rectangular cylinders with a long side normal to the flow. J. Fluid Mech. 180, 171–191.Google Scholar
Names, A., Zhao, J. S., Jacono, D. L. & Sheridan, J. 2012 The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack. J. Fluid Mech. 710, 102–130.Google Scholar
Naudascher, E. & Rockwell, D. 1994 Flow-induced Vibrations: An Engineering Guide. Dover.Google Scholar
Navrose & Mittal, S. 2016 Lock-in in vortex-induced vibration. J. Fluid Mech. 794, 565–594.Google Scholar
Païdoussis, M. P., Price, S. J. & de Langre, E. 2010 Fluid–Structure Interactions: Cross-flow-induced Instabilities. Cambridge University Press.Google Scholar
Park, D. & Yang, K. S. 2016 Flow instabilities in the wake of a rounded square cylinder. J. Fluid Mech. 793, 915–932.Google Scholar
Parkinson, G. 1989 Phenomena and modelling of flow-induced vibrations of bluff bodies. Prog. Aerosp. Sci. 26, 169–224.Google Scholar
Parkinson, G. & Wawzonek, M. 1981 Some considerations of combined effects of galloping and vortex resonance. J. Wind Engng Ind. Aerodyn. 8, 135–143.Google Scholar
Rowley, C. W. & Dawson, S. T. 2017 Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 49, 387–417.Google Scholar
Rowley, C. W., Mezic, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Sen, S. & Mittal, S. 2011 Free vibration of a square cylinder at low Reynolds numbers. J. Fluids Struct. 27, 875–884.Google Scholar
Sen, S. & Mittal, S. 2015 Effect of mass ratio on free vibrations of a square cylinder at low Reynolds numbers. J. Fluids Struct. 54, 661–678.Google Scholar
Singh, S. P. & Mittal, S. 2005 Vortex-induced oscillations at low Reynolds numbers: hysteresis and vortex-shedding modes. J. Fluids Struct. 20, 1085–1104.Google Scholar
Tamura, Y. & Matsui, G. 1979 Wake-oscillator model of vortex-induced oscillation of circular cylinder. In Proceedings of the 5th International Conference on Wind Engineering, Fort Collins, USA, pp. 1085–1094. Elsevier.Google Scholar
Tamura, Y. & Shimada, K.1987 A mathematical model for the transverse oscillations of square cylinder. The Academic Reports, the Faculty of Engineering, Tokyo Institute of Polytechnic, vol. 9, pp. 56–62.Google Scholar
Wanderley, J. B. V. & Levi, C. A. 2002 Validation of a finite difference method for the simulation of vortex-induced vibrations on a circular cylinder. Ocean Engng 29, 445–460.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.Google Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.Google Scholar
Yao, W. & Jaiman, R. K. 2017 Model reduction and mechanism for the vortex-induced vibrations of bluff bodies. J. Fluid Mech. 827, 357–393.Google Scholar
Yoon, D. H., Yang, K. S. & Choi, C. B. 2010 Flow past a square cylinder with an angle of incidence. Phys. Fluids 22, 043603.Google Scholar
Zhang, W., Jiang, Y. & Ye, Z. 2007 Two better loosely coupled solution algorithms of CFD based aeroelastic simulation. Engng Appl. Comput. Fluid. 1, 253–262.Google Scholar
Zhang, W., Li, X., Ye, Z. & Jiang, Y. 2015a Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers. J. Fluid Mech. 783, 72–102.Google Scholar
Zhang, W., Liu, Y. & Li, J. 2015b A simple strategy for capturing the unstable steady solution of an unsteady flow. Open J. Fluid Dyn. 5, 188–198.Google Scholar
Zhao, J. S., Leontini, J. S., Jacono, D. L. & Sheridan, J. 2014 Fluid structure interaction of a square cylinder at different angles of attack. J. Fluid Mech. 747, 688–721.Google Scholar
Zhao, J. S., Nemes, A., Jacono, D. L. & Sheridan, J. 2018 Branch/mode competition in the flow-induced vibration of a square cylinder. Phil. Trans. R. Soc. Lond. A 376, 20170243.Google Scholar
Zhao, M., Cheng, L. & Zhou, T. 2013 Numerical simulation of vortex-induced vibration of a square cylinder at a low Reynolds number. Phys. Fluids 25, 023603.Google Scholar
Zhu, C. & So, R. M. C. 2000 Fluid damping of an elastic cylinder in a cross-flow. J. Fluids Struct. 14, 303–322.Google Scholar