Hostname: page-component-84b7d79bbc-x5cpj Total loading time: 0 Render date: 2024-07-28T03:52:49.889Z Has data issue: false hasContentIssue false
  • English
  • Français

A new idea to predict reshocked Richtmyer–Meshkov mixing: constrained large-eddy simulation

Published online by Cambridge University Press:  11 May 2021

Yuanwei Bin Open the ORCID record for Yuanwei Bin [Opens in a new window] ,
Mengjuan Xiao Open the ORCID record for Mengjuan Xiao [Opens in a new window] ,
Yipeng Shi Open the ORCID record for Yipeng Shi [Opens in a new window] ,
Yousheng Zhang Open the ORCID record for Yousheng Zhang [Opens in a new window]  and
Shiyi Chen Open the ORCID record for Shiyi Chen [Opens in a new window]
Yuanwei Bin
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Peking University, Beijing100871, PR China
Mengjuan Xiao
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing100094, PR China
Yipeng Shi*
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Peking University, Beijing100871, PR China Center for Applied Physics and Technology, HEDPS, and College of Engineering, Peking University, Beijing100871, PR China
Yousheng Zhang*
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing100094, PR China Center for Applied Physics and Technology, HEDPS, and College of Engineering, Peking University, Beijing100871, PR China
Shiyi Chen
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Peking University, Beijing100871, PR China Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, Guangdong518055, PR China
*
†Email addresses for correspondence: syp@mech.pku.edu.cn, zhang_yousheng@iapcm.ac.cn
†Email addresses for correspondence: syp@mech.pku.edu.cn, zhang_yousheng@iapcm.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

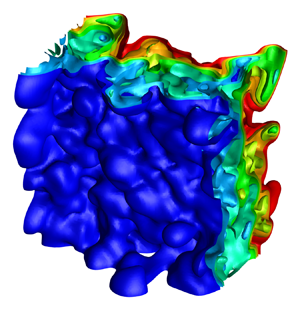
The reshocked turbulent Richtmyer–Meshkov (RM) mixing of two media is the most representative problem of more general and complex turbulent mixing induced by interfacial instabilities, broadly occurring in both nature and engineering applications. An accurate prediction of its evolving of spatial structure and mixing width (MW) is of fundamental importance. However, satisfactory prediction with the large-eddy simulation (LES) has not yet been achieved, even for the most important MW. In this paper, we innovatively solve this problem by combining the idea of the constrained large-eddy simulation (CLES), which succeeded previously only in classical single-medium turbulence, and our recently developed Reynolds averaged Navier–Stokes (RANS) model, which realized a satisfactory prediction of MW. Specifically, in our currently developed CLES model, with the aid of Reynolds decomposition, the unclosed subgrid scale (SGS) LES model is decomposed into two parts, i.e. the averaged and the fluctuating. The averaged part is dominated and modelled by the counterpart of our recently developed RANS model to accurately predict the MW, while the fluctuating part is modelled with the classical Smagorinsky model. Consequently, besides successfully capturing the three-dimensional large-scale structure of turbulence and the evolution of the (normalized) mixed mass, our newly proposed CLES also predicts a satisfactory MW with a very coarse grid. To the best of our knowledge, this is the first time that the LES can yield such a comparable result with experiment.

JFM classification

Compressible Flows: Shock waves Mixing: Turbulent mixing Turbulent Flows: Turbulence modelling
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 918 , 10 July 2021 , R1
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Chen, S., Xia, Z., Pei, S., Wang, J., Yang, Y., Xiao, Z. & Shi, Y. 2012 Reynolds-stress-constrained large-eddy simulation of wall-bounded turbulent flows. J. Fluid Mech. 703, 1–28.CrossRefGoogle Scholar
Garnier, E., Adams, N. & Sagaut, P. 2009 Large Eddy Simulation for Compressible Flows. Springer Science & Business Media.CrossRefGoogle Scholar
Grinstein, F.F., Gowardhan, A.A. & Wachtor, A.J. 2011 Simulations of Richtmyer–Meshkov instabilities in planar shock-tube experiments. Phys. Fluids 23 (3), 034106.CrossRefGoogle Scholar
von Helmholtz, H. 1868 Über discontinuirliche Flüssigkeits-Bewegungen. Akademie der Wissenschaften zu Berlin.Google Scholar
Hill, D.J., Pantano, C. & Pullin, D.I. 2006 Large-eddy simulation and multiscale modelling of a Richtmyer–Meshkov instability with reshock. J. Fluid Mech. 557, 29–61.CrossRefGoogle Scholar
Jiang, G.-S. & Shu, C.-W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126 (1), 202–228.CrossRefGoogle Scholar
Jiang, Z., Xiao, Z., Shi, Y. & Chen, S. 2013 Constrained large-eddy simulation of wall-bounded compressible turbulent flows. Phys. Fluids 25 (10), 106102.CrossRefGoogle Scholar
Kelvin, L. 1871 On the motion of free solids through a liquid. Phil. Mag. 42 (281), 362–377.Google Scholar
Kim, K.H. & Kim, C. 2005 Accurate, efficient and monotonic numerical methods for multi-dimensional compressible flows. J. Comput. Phys. 208 (2), 527–569.CrossRefGoogle Scholar
Kraichnan, R.H. 1985 Decimated amplitude equations in turbulence dynamics. In Theoretical Approaches to Turbulence (ed. D.L. Dwoyer & M.Y. Hussaini), pp. 91–135. Springer.CrossRefGoogle Scholar
Lindl, J.D., McCrory, R.L. & Campbell, E.M. 1992 Progress toward ignition and burn propagation in inertial confinement fusion. Phys. Today 45 (9), 32.CrossRefGoogle Scholar
Meshkov, E.E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4 (5), 101–104.CrossRefGoogle Scholar
Rayleigh, Lord 1884 On the circulation of air observed in Kundt's tubes, and on some allied acoustical problems. Phil. Trans. R. Soc. Lond. A 175, 1–21.Google Scholar
Remington, B.A., Drake, R.P., Takabe, H. & Arnett, D. 2000 A review of astrophysics experiments on intense lasers. Phys. Plasmas 7 (5), 1641–1652.CrossRefGoogle Scholar
Richtmyer, R.D. 1954 Taylor instability in shock acceleration of compressible fluids. Tech. Rep. LA-1914. Los Alamos Scientific Laboratory, New Mexico.Google Scholar
Schilling, O. & Latini, M. 2010 High-order WENO simulations of three-dimensional reshocked Richtmyer–Meshkov instability to late times: dynamics, dependence on initial conditions, and comparisons to experimental data. Acta Mathematica 30 (2), 595–620.CrossRefGoogle Scholar
Taylor, G.I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 201 (1065), 192–196.Google Scholar
Toro, E.F. 2013 Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction. Springer Science & Business Media.Google Scholar
Toro, E.F., Spruce, M. & Speares, W. 1994 Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 4 (1), 25–34.CrossRefGoogle Scholar
Tritschler, V.K., Olson, B.J., Lele, S.K., Hickel, S., Hu, X.Y. & Adams, N.A. 2014 On the Richtmyer–Meshkov instability evolving from a deterministic multimode planar interface. J. Fluid Mech. 755, 429–462.CrossRefGoogle Scholar
Tritschler, V.K., Hickel, S., Hu, X.Y. & Adams, N.A. 2013 On the Kolmogorov inertial subrange developing from Richtmyer–Meshkov instability. Phys. Fluids 25 (7), 071701.CrossRefGoogle Scholar
Ukai, S., Genin, F., Srinivasan, S. & Menon, S. 2009 Large eddy simulation of re-shocked Richtmyer–Meshkov instability. In 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, p. 944.Google Scholar
Vetter, M. & Sturtevant, B. 1995 Experiments on the Richtmyer–Meshkov instability of an $\textrm {air}/\textrm {SF}_6$ interface. Shock Waves 4 (5), 247–252.CrossRefGoogle Scholar
Xiao, M., Zhang, Y. & Tian, B. 2020 a Modeling of turbulent mixing with an improved K–L model. Phys. Fluids 32 (9), 092104.CrossRefGoogle Scholar
Xiao, M., Zhang, Y. & Tian, B. 2020 b Unified prediction of reshocked Richtmyer–Meshkov mixing with K–L model. Phys. Fluids 32 (3), 032107.Google Scholar
Zhang, Y.-s., He, Z.-w., Xie, H.-s., Xiao, M.-J. & Tian, B.-l. 2020 a Methodology for determining coefficients of turbulent mixing model. J. Fluid Mech. 905, A26.CrossRefGoogle Scholar
Zhang, Y.-s., Ni, W.-d., Ruan, Y.-c. & Xie, H.-s. 2020 b Quantifying mixing of Rayleigh–Taylor turbulence. Phys. Rev. Fluids 5, 104501.CrossRefGoogle Scholar
Zhou, Y. 2017 a Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 720–722, 1–136.Google Scholar
Zhou, Y. 2017 b Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II. Phys. Rep. 723–725, 1–160.Google Scholar
Zhou, Y., Cabot, W.H. & Thornber, B. 2016 Asymptotic behavior of the mixed mass in Rayleigh–Taylor and Richtmyer–Meshkov instability induced flows. Phys. Plasmas 23 (5), 052712.CrossRefGoogle Scholar
Zhou, Y., Clark, T.T., Clark, D.S., Gail Glendinning, S., Aaron Skinner, M., Huntington, C.M., Hurricane, O.A., Dimits, A.M. & Remington, B.A. 2019 Turbulent mixing and transition criteria of flows induced by hydrodynamic instabilities. Phys. Plasmas 26 (8), 080901.CrossRefGoogle Scholar