2. Problem formulation

Consider a two-dimensional configuration where a circular disc of radius $a$ is suspended freely in an unbounded liquid solution (solute diffusivity $D$). The reference solute concentration at large distances from the disc is denoted by $c_\infty$. The chemical activity at the particle boundary is modelled as a first-order chemical reaction (Ebbens et al. Reference Ebbens, Tu, Howse and Golestanian2012; Michelin & Lauga Reference Michelin and Lauga2014)

(2.1)\begin{equation} \text{solute absorption (per unit area)} = k \times \text{local value of solute concentration}, \end{equation}

where the (positive) rate constant $k$ generally varies along the circumference. We assume that the distribution of $k$ is symmetric about a diameter of the circle. The circumferential average of $k$ is denoted by $\bar {k}$.

We employ a macroscale description, where the short-range interaction between the solute molecules and the particle is expressed by an effective diffusio-osmotic slip (Anderson Reference Anderson1989). Thus in a particle-fixed system, the standard no-slip condition is replaced by

(2.2)\begin{equation} \text{slip velocity} = b \times \text{surface gradient of solute concentration}.\end{equation}

Following common practice (Michelin & Lauga Reference Michelin and Lauga2014; Sondak et al. Reference Sondak, Hawley, Heng, Vinsonhaler, Lauga and Thiffeault2016), we assume that the slip coefficient $b$ is uniform. Note that $b$ is a signed quantity, positive for repulsive interactions and negative for attractive ones. The velocity scale associated with (2.2) is

(2.3)\begin{equation} \mathcal{U} = \frac{|b|\,c_\infty}{a}. \end{equation}

Defining the intrinsic Péclet number $\textit {Pe}$ as $a \, \mathcal {U}/D$ thus gives

(2.4)\begin{equation} \textit{Pe} = \frac{|b|\,c_\infty}{D}. \end{equation}

It follows from the problem symmetry that the force- and torque-free cylinder reacts to the interfacial slip by translating along its symmetry diameter at a constant velocity, without rotating. The translation velocity, denoted by $s$, is reckoned positive when the particle propagates in the direction of its more active hemicircle. (This definition will be made precise later on; see (3.12).) Our goal is the determination of this velocity.

3. Dimensionless formulation

In what follows, we normalise all length variables by $a$. The analysis is carried out in a particle-fixed reference system with origin at the disc centre. In that system, we use $(x,y)$ Cartesian coordinates defined such that the $x$-axis is aligned along the symmetry diameter of the particle, pointing in the direction of the more active hemicircle. Additionally, we utilise $(r,\theta )$ polar coordinates, with $\theta$ measured in the counterclockwise direction from the $x$-axis. Accordingly, the distribution of the rate constant $k$ is denoted by $k(\theta )$. The dimensionless geometry is portrayed in figure 1.

Figure 1. Schematic of the dimensionless geometry, indicating the dimensionless differential equations and boundary conditions.

We employ a dimensionless notation where the solute concentration is normalised by $c_\infty$ and the velocity field is normalised by $\mathcal {U}$. Our interest is in the velocity $U(=s/\mathcal {U} )$ of the particle relative to the otherwise quiescent liquid; in the particle-fixed reference frame, this velocity is manifested as the uniform streaming $-U \boldsymbol {\hat {\imath }}$ at infinity, $\boldsymbol {\hat {\imath }}$ being a unit vector in the $x$-direction.

To obtain this velocity, we consider the coupled problem governing the solute-concentration distribution $c$ and velocity field $\boldsymbol {u}$. The solute-transport problem is governed by: (i) the advection–diffusion equation,

(3.1)\begin{equation} \nabla^{2} c = \textit{Pe} \, \boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla} c \quad \text{for} \ r>1; \end{equation}

(ii) the approach to the reference concentration at large distances,

(3.2)\begin{equation} \lim_{r\to\infty}c = 1; \end{equation}

and (iii) the kinetic condition at the particle boundary,

(3.3)\begin{equation} \frac{\partial c}{\partial r} = \textit{Da} \, F(\theta)\,c\quad \text{at} \ r=1,\end{equation}

where

(3.4)\begin{equation} F(\theta) = {k(\theta)}/{\bar{k}} \end{equation}

is the dimensionless distribution of rate constant, and

(3.5)\begin{equation} \textit{Da} = \frac{a\bar{k}}{D} \end{equation}

is the Damköhler number, representing the ratio of diffusive ($a^{2}/D$) to reactive ($a/\bar {k}$) time scales.

The velocity field $\boldsymbol {u} = \hat {\boldsymbol {e}}_r u + \hat {\boldsymbol {e}}_\theta v$ is governed by: (i) the continuity and Stokes equations (the former tacitly employed in (3.1)); (ii) the impermeability condition

(3.6)\begin{equation} u = 0 \quad \text{at} \ r=1; \end{equation}

(iii) the slip condition (cf. (2.2))

(3.7)\begin{equation} v = M\,\frac{\partial c}{\partial \theta} \quad \text{at} \ r=1, \end{equation}

where $M=b/|b|$; (iv) the far-field approach to a uniform stream,

(3.8)\begin{equation} \lim_{r\to\infty}\boldsymbol{u} ={-} U \boldsymbol{\hat{\imath}} ; \end{equation}

and (v) the requirement that the particle is force-free. The latter, in conjunction with (3.7) and (3.8), provides the particle velocity as a quadrature (Squires & Bazant Reference Squires and Bazant2006),

(3.9)\begin{equation} U = \frac{M}{2{\rm \pi}}\int_{-{\rm \pi}}^{\rm \pi} \left.\frac{\partial c}{\partial \theta}\right|_{r=1} \sin\theta \, \mathrm{d} \theta. \end{equation}

In principle, the above pair of problems provides $U$ as a (nonlinear) functional of $F$ and a (nonlinear) function of $\textit {Pe}$, $\textit {Da}$ and $M$. Note that $\textit {Pe}$ and $\textit {Da}$ are positive parameters, while $M=\pm 1$.

The inhomogeneous circumferential reaction is described in condition (3.3) by the distribution $F(\theta )$, which is required to be strictly positive:

(3.10)\begin{equation} F(\theta)>0 \quad \text{for} \ {-{\rm \pi}}<\theta<{\rm \pi}. \end{equation}

By definition of $\bar {k}$ it follows that $F$ satisfies the integral constraint

(3.11)\begin{equation} \int_{-{\rm \pi}}^{\rm \pi} F(\theta) \, \mathrm{d}\theta = 2{\rm \pi}. \end{equation}

Also, recalling the sense of direction of the $x$-axis, we impose the constraint

(3.12)\begin{equation} \int_{-{\rm \pi}/2}^{{\rm \pi}/2} F(\theta) \, \mathrm{d}\theta > {\rm \pi}. \end{equation}

Now, the symmetry of the $k$ distribution about the $x$-axis implies that $F$ is even, i.e.

(3.13)\begin{equation} F(-\theta) = F(\theta), \end{equation}

so that (3.11) and (3.12) may be written as

(3.14a,b)\begin{equation} \int_0^{\rm \pi} F(\theta) \, \mathrm{d}\theta = {\rm \pi}, \quad \int_0^{{\rm \pi}/2} F(\theta) \, \mathrm{d}\theta > \frac{\rm \pi}{2}. \end{equation}

With activity higher on the right hemicircle, one expects the solute concentration about that hemicircle to be lower than the corresponding concentration about the left hemicircle. The associated solute gradients are then expected, in some average sense, to point from right to left. For $M=1$, this would apply slip at the same direction, whence particle motion to the right, whereby $U>0$ (see indeed (3.9)). For $M=-1$, one would then expect ${U<0}$. The preceding crude arguments may seem to suggest that

(3.15)\begin{equation} MU>0. \end{equation}

A stronger version of the odd dependence (3.15) holds when $U$ is proportional to $M$:

(3.16)\begin{equation} U \propto M. \end{equation}

This version of (3.15) holds in the linear problem that applies (in three dimensions) in the absence of solute advection. It was also observed in a small-$\textit {Pe}$ analysis in two dimensions (Yariv & Crowdy Reference Yariv and Crowdy2020).

Since we did not prove property (3.15), it remains questionable for the time being.

4. Simplifications

The nonlinear problem formulated in § 3 clearly admits the symmetries

(4.1a–c)\begin{equation} c(-\theta) = c(\theta), \quad u(-\theta) = u(\theta), \quad v(-\theta) ={-}v(\theta). \end{equation}

It is therefore sufficient to analyse the problem in the domain $0<\theta <{\rm \pi}$.

A further simplification follows by making use of a streamfunction $\psi$, defined by

(4.2a,b)\begin{equation} u = \frac{\partial\psi}{r\,\partial\theta}, \quad v ={-}\frac{\partial \psi}{\partial r}. \end{equation}

The continuity equation is then satisfied trivially, while the Stokes equation governing $\boldsymbol {u}$ is transformed to the biharmonic equation governing $\psi$:

(4.3)\begin{equation} \nabla^{4}\psi=0 \quad \text{for} \ r>1. \end{equation}

The impermeability condition (3.6) implies that $\psi$ is a constant at $r=1$. Since $\psi$ is defined to within an additive constant, we simply write

(4.4)\begin{equation} \psi=0 \quad \text{at} \ r=1. \end{equation}

In terms of $\psi$, the slip and far-field conditions (3.7) and (3.8) read, respectively

(4.5)$$\begin{gather} \frac{\partial \psi}{\partial r} ={-}M\,\frac{\partial c}{\partial \theta} \quad \text{at} \ r=1, \end{gather}$$

(4.6)$$\begin{gather}\psi \sim{-}Ur\sin\theta \quad \text{as} \ r\to\infty, \end{gather}$$

while the symmetries (4.1a–c) imply that

(4.7)\begin{equation} \psi(-\theta) ={-}\psi(\theta). \end{equation}

Finally, we note that in term of $\psi$, the advection–diffusion equation (3.1) becomes

(4.8)\begin{equation} \nabla^{2} c = \frac{\textit{Pe}}{r}\,\frac{\partial (c,\psi)}{\partial (r,\theta)} \quad \text{for} \ r>1. \end{equation}

5. Weak inhomogeneity

We write

(5.1)\begin{equation} F(\theta) = 1+ \epsilon\,f(\theta), \end{equation}

where

(5.2)\begin{equation} \epsilon>0. \end{equation}

From (3.13), (3.14a,b) and (5.2), we find that $f$ satisfies the respective properties

(5.3a–c)\begin{equation} f(-\theta) = f(\theta), \quad \int_0^{\rm \pi} f(\theta) \, \mathrm{d}\theta = 0, \quad \int_0^{{\rm \pi}/2} f(\theta) \, \mathrm{d}\theta \left(={-} \int_{{\rm \pi}/2}^{\rm \pi} f(\theta) \, \mathrm{d}\theta\right) > 0. \end{equation}

In addition, we impose the constraint (without any loss of generality)

(5.4)\begin{equation} \max_{[0,{\rm \pi}]}|f(\theta)| = 1. \end{equation}

It then follows from (3.10) that

(5.5)\begin{equation} \epsilon<1. \end{equation}

Examples of distributions that satisfy properties (5.3a–c) and (5.4) are the cosine distribution

(5.6)\begin{equation} f(\theta)=\cos\theta \end{equation}

and the Janus distribution

(5.7)\begin{equation} f(\theta)=\left\{ \begin{array}{@{}ll} 1, & 0<|\theta|<{\rm \pi}/2,\\ -1, & {\rm \pi}/2<|\theta|<{\rm \pi}. \end{array} \right. \end{equation}

In terms of $\epsilon$ and $f$, the absorption condition (3.3) becomes

(5.8)\begin{equation} \frac{\partial c}{\partial r} = \textit{Da} \,c [1+ \epsilon\,f(\theta)] \quad \text{at } r=1.\end{equation}

With the norm of $f$ set to $\operatorname {ord}(1)$ by (5.4), the parameter $\epsilon$ may be interpreted as an effective measure of interfacial inhomogeneity. To capture the case of weak inhomogeneity, we consider the asymptotic limit $\epsilon \searrow 0$. We expand all pertinent field variables in the generic form

(5.9)\begin{equation} g(r,\theta;\epsilon) = g_0(r,\theta) + \epsilon\,g_1(r,\theta) + \cdots. \end{equation}

This results in the respective expansion of $U$:

(5.10)\begin{equation} U = U_0 + \epsilon U_1 + \cdots. \end{equation}

6. Breakdown of the weak-advection approximation

At $\operatorname {ord}(1)$, condition (5.8) becomes radially symmetric:

(6.1)\begin{equation} \frac{\partial c_0}{\partial r} = \textit{Da} \,c_0 \quad \text{at} \ r=1.\end{equation}

In the absence of flow at $\operatorname {ord}(1)$, the right-hand side of (4.8) vanishes at this order. It then follows that $c_0$ is governed by Laplace's equation

(6.2)\begin{equation} \nabla^{2} c_0 = 0 \quad \text{for} \ r>1. \end{equation}

We anticipate that the solution of (6.1) and (6.2) is radially symmetric for all $r$. Conversely, with a radially symmetric $c_0$, no flow is animated by the slip condition (3.7). We therefore proceed assuming that

(6.3)\begin{equation} c_0 \text{ is a function of $r$ alone},\end{equation}

and that $\boldsymbol {u}_0$ (and hence $\psi _0$) vanish trivially. Consequently,

(6.4)\begin{equation} U_0=0. \end{equation}

Substituting (6.3) into (6.1) and (6.2), we obtain

(6.5)\begin{equation} c_0 = a_0 (\textit{Da} \ln r +1). \end{equation}

The integration constant $a_0$ cannot be determined from the $\operatorname {ord}(1)$ balance of the far-field condition (3.2),

(6.6)\begin{equation} \lim_{r\to\infty}c_0=1, \end{equation}

which is incompatible with (6.5).

The above incompatibility is associated with the breakdown of the dominance of diffusion, associated via (6.2) with the small-$\epsilon$ limit. Indeed, the solution (6.5) implies that the presumably $\operatorname {ord}(\epsilon )$ advective term in (3.1) becomes comparable to the diffusive term at distances $r=\operatorname {ord}(\epsilon ^{-1})$. As a consequence of the above non-uniformity, we need to employ two separate asymptotic expansions of $c$. The first, holding at $\operatorname {ord}(1)$ distances from the disc (the ‘nearby’ region), is provided by the generalisation of (5.9)

(6.7)\begin{equation} g(r,\theta;\epsilon) = g_0(r,\theta;\epsilon) + \epsilon\,g_1(r,\theta;\epsilon) + \cdots, \end{equation}

where we allow for a weak (i.e. logarithmic) dependence upon $\epsilon$ at each order. The second expansion holds at the ‘remote’ region, where $r=\operatorname {ord}(\epsilon ^{-1})$. Towards that end, we employ the stretched radial coordinate

(6.8)\begin{equation} r' = \epsilon r , \end{equation}

which is $\operatorname {ord}(1)$ in the remote region. Employing the change of variables

(6.9)\begin{equation} c(r,\theta;\epsilon) = c'(r',\theta;\epsilon), \end{equation}

the remote region expansion is

(6.10)\begin{equation} c'(r',\theta;\epsilon) = c'_0(r',\theta;\epsilon) + \epsilon\,c'_1(r',\theta;\epsilon) + \cdots,\end{equation}

where again we allow for a logarithmic dependence upon $\epsilon$ at each asymptotic order. The use of generalised Poincaré expansions, where the terms are allowed to depend upon $\ln \epsilon$, enables a straightforward use of the Van Dyke matching rule, where logarithmically large terms are considered on a par with $\operatorname {ord}(1)$ terms (Hinch Reference Hinch1991).

Two points are worth noting: First, the far-field decay (3.2) now applies on $c'$:

(6.11)\begin{equation} \lim_{r'\to\infty}c' = 1. \end{equation}

No far-field condition applies on the nearby field $c$, which describes the concentration only for $r=\operatorname {ord}(1)$. Thus the distribution (6.5), obtained prior to the identification of two length scales, remains valid (with $a_0$ being allowed to depend weakly upon $\epsilon$). Since (3.9) clearly applies in the nearby region, (6.4) is also retained. Instead of the far-field condition (3.2), the nearby concentration $c$ must satisfy appropriate large-$r$ conditions that follow from the requirement of asymptotic matching with the remote concentration. These conditions determine uniquely the integration constants appearing in the various $\{c_i\}$ (e.g. $a_0$ in (6.5)).

Second, the velocity field is affected by the solute concentration only through the slip condition (3.7), which applies at $r=1$. Accordingly, there is no need for a separate expansion of the velocity field, akin to (6.10), at the remote region. The only modification required in the expansion of the velocity field is the transition from (5.9) to (6.7).

Defining the remote-region gradient operator $\boldsymbol {\nabla }' = \epsilon ^{-1} \boldsymbol {\nabla }$, solute transport in that region is governed by (cf. (3.1))

(6.12)\begin{equation} \epsilon\,{\nabla'}^{2} c' = \textit{Pe} \, \boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla}' c', \end{equation}

wherein $\boldsymbol {u}$ is to be evaluated at $r=\operatorname {ord}(\epsilon ^{-1})$.

7. Leading-order remote solution

Given condition (3.8) and observation (6.4), the velocity in the remote region is simply given at leading order by constant vector $-\epsilon \,\boldsymbol {\hat {\imath }}\, U_1$. Consequently, the leading-order balance of (6.12) becomes

(7.1)\begin{equation} {\nabla'}^{2} c'_0 ={-}\textit{Pe} \, U_1\,\frac{\partial c'_0}{\partial x'}, \end{equation}

wherein $x'=\epsilon x$ is a stretched Cartesian coordinate (cf. (6.8)). This equation is supplemented by the leading-order balance of (6.11), namely

(7.2)\begin{equation} \lim_{r'\to\infty}c'_0 = 1. \end{equation}

Writing

(7.3)\begin{equation} c_0' = 1 + G, \end{equation}

we find that $G$, which decays at large $r'$, also satisfies (7.1). Substituting

(7.4)\begin{equation} G = \exp\left(-\tfrac{1}{2}\textit{Pe} \, U_1x'\right)H, \end{equation}

we find that $H$ satisfies the modified Helmholtz equation

(7.5)\begin{equation} \nabla'^{2} H = \tfrac{1}{4}\textit{Pe}^{2}\,U_1^{2} H. \end{equation}

The solution of that equation that decays at large $r'$ and is least singular at $r'=0$ is a radially symmetric screened source, $\mathrm {K}_0({\textit {Pe}\,|U_1|\,r'}/{2})$, in which $\mathrm {K}_0$ is the modified Bessel function of the second kind. While all spatial derivatives of that source also satisfy (7.5), they are too singular at the origin and are excluded by the requirement of asymptotic matching with (6.5). We therefore obtain

(7.6)\begin{equation} c'_0= 1+\frac{Q}{2{\rm \pi}} \exp\left({-\tfrac{1}{2}\textit{Pe} \,U_1x'}\right) \mathrm{K}_0\left( \frac{\textit{Pe}\,|U_1|\,r'}{2} \right), \end{equation}

where the source magnitude $Q$ remains to be determined. Using the small-argument behaviour of $\mathrm {K}_0$ (Abramowitz & Stegun Reference Abramowitz and Stegun1965), we find

(7.7)\begin{equation} c'_0 \sim 1-\frac{Q}{2{\rm \pi}} \left(\ln\frac{\textit{Pe}\,|U_1|\,r'}{4} + \gamma\right) \quad \text{as} \ r'\to 0, \end{equation}

wherein $\gamma$ is the Euler–Mascheroni constant. The asymptotic error in (7.7) is ‘algebraically small’ in $r'$, i.e. smaller than some positive power of $r'$.

We now perform Van Dyke $\operatorname {ord}(1):\operatorname {ord}(1)$ matching, using (6.5). Comparison of the $\ln r$ terms gives

(7.8)\begin{equation} Q={-}2{\rm \pi} a_0\,\textit{Da}. \end{equation}

Comparison of the $r$-independent terms then yields

(7.9)\begin{equation} a_0 = \left[1+\textit{Da}\left( \ln\frac{4}{\epsilon\,\textit{Pe}\,|U_1|}- \gamma \right) \right]^{{-}1}. \end{equation}

We have therefore evaluated $c_0$ in terms of the (as yet unknown) leading-order particle velocity. To obtain that velocity, we need to consider deviations from radial symmetry in the nearby region.

8. Deviations from radial symmetry

Making use of (6.3), we find from (4.8) at $\operatorname {ord}(\epsilon )$ that $c_1$ satisfies the equation

(8.1)\begin{equation} \nabla^{2} c_1 = \frac{\textit{Pe}}{r}\,\frac{\partial\psi_1}{\partial\theta}\, \frac{\mathrm{d} c_0}{\mathrm{d} r}.\end{equation}

It also satisfies the boundary condition

(8.2)\begin{equation} \frac{\partial c_1}{\partial r}-\textit{Da}\, c_1 = \textit{Da} \,c_0\,f(\theta) \quad \text{at} \ r=1,\end{equation}

obtained from (5.8) at $\operatorname {ord}(\epsilon )$.

Towards formulating the far-field condition governing $c_1$, we expand $c'_0$ at small $r'$ up to $\operatorname {ord}(r')$, thus obtaining the following refinement of (7.7):

(8.3)\begin{equation} c'_0 \sim 1+a_0\,\textit{Da} \left(\ln\frac{\textit{Pe}\,|U_1|\,r'}{4} + \gamma\right)\left(1 - \tfrac{1}{2}\textit{Pe} \,U_1r'\cos\theta\right)\quad \text{as} \ r'\to 0, \end{equation}

where we have made use of (7.8). It is seen readily that the asymptotic error in (8.3) is ‘algebraically smaller’ than $r'$, meaning that its ratio to $r'$ is algebraically small in $r'$. Making use of Van Dyke $\operatorname {ord}(1):\operatorname {ord}(\epsilon )$ matching, we obtain the following condition on $c_1$:

(8.4)\begin{equation} c_1 \sim \tfrac{1}{2}\textit{Pe} \,U_1 a_0\,\textit{Da} \left(\ln\frac{4}{\epsilon\,\textit{Pe}\,|U_1| r}- \gamma\right) r\cos\theta \quad \text{as} \ r\to\infty. \end{equation}

It is evident from both the far-field behaviour (8.4) and the forcing terms in (8.1) and (8.2) that $c_1$ lacks radial symmetry. The integral expression (3.9) then implies a non-zero $U_1$:

(8.5)\begin{equation} U_1 = \frac{M}{2{\rm \pi}}\int_{-{\rm \pi}}^{\rm \pi} \left.\frac{\partial c_1}{\partial \theta}\right|_{r=1} \sin\theta \, \mathrm{d} \theta, \end{equation}

consistently with the analysis of solute transport in the remote region.

Our first objective is to determine the general form of $\psi _1$. This field is governed by: (i) the biharmonic equation (see (4.3)); (ii) the impermeability condition (cf. (4.4))

(8.6)\begin{equation} \psi_1=0 \quad \text{at} \ r=1;\end{equation}

(iii) the far-field condition (cf. (4.6))

(8.7)\begin{equation} \psi_1 \sim{-}U_1r\sin\theta \quad \text{as} \ r\to\infty; \end{equation}

(iv) the symmetry condition (cf. (4.7))

(8.8)\begin{equation} \psi_1(-\theta) ={-}\psi_1(\theta); \end{equation}

(v) the requirement of a force-free disc; and (vi) the slip condition (cf. (4.5))

(8.9)\begin{equation} \frac{\partial \psi_1}{\partial r} ={-}M\,\frac{\partial c_1}{\partial \theta} \quad \text{at} \ r=1.\end{equation}

Given the general structure of single-valued solutions of the biharmonic equation in polar coordinates (Leal Reference Leal2007), we find that the force-free solution that satisfies (8.6)–(8.8) is

(8.10)\begin{equation} \psi_1 ={-}U_1\left(r - \frac{1}{r}\right) \sin\theta + \sum_{n=2}^{\infty} \alpha^{(n)} (r^{{-}n}-r^{2-n})\sin n \theta. \end{equation}

In principle, the velocity $U_1$ and the set $\{\alpha ^{(n)}\}$ are determined from the slip condition (8.9). We therefore head to the calculation of $c_1$.

Substituting (6.5) and (8.10) into (8.1), we obtain the Poisson equation

(8.11)\begin{equation} \nabla^{2} c_1 = {\textit{Pe}}\, a_0\,\textit{Da} \left[U_1 \left(\frac{1}{r^{3}}-\frac{1}{r}\right) \cos\theta + \sum_{n=2}^{\infty} n \alpha^{(n)} (r^{{-}n-2}-r^{{-}n})\cos n \theta\right].\end{equation}

Also, substitution of (6.5) into (8.2) yields the condition

(8.12)\begin{equation} \frac{\partial c_1}{\partial r}-\textit{Da}\, c_1 = \textit{Da} \,a_0\,f(\theta) \quad \text{at} \ r=1.\end{equation}

In addition to (8.11) and (8.12), $c_1$ must also satisfy the matching condition (8.4).

We note that condition (5.3a) implies a cosine series representation for $f$, say

(8.13)\begin{equation} f(\theta) = \sum_{n=0}^{\infty} f^{(n)} \cos n\theta, \end{equation}

wherein

(8.14)\begin{equation} f^{(n)} = \frac{2}{\rm \pi} \int_0^{\rm \pi} f(\vartheta)\cos n\vartheta\, \mathrm{d}\vartheta \end{equation}

are the associated Fourier coefficients. We write $c_1$ as a sum of corresponding Fourier modes:

(8.15)\begin{equation} c_1(r,\theta) = \sum_{n=0}^{\infty} c^{(n)}(r) \cos n \theta. \end{equation}

Substituting into (8.5) and making use of the orthogonality of the set $\{\cos n\theta \}_{n=0}^{\infty }$, we obtain

(8.16)\begin{equation} U_1 ={-}\frac{M}{2}\,c^{(1)}(1). \end{equation}

Given the linear problem governing $c_1$, we can exploit that orthogonality further and seek only $c^{(1)}(r)$. This function satisfies the inhomogeneous equation (cf. (8.11))

(8.17)\begin{equation} \frac{\mathrm{d} ^{2}c^{(1)}}{\mathrm{d} r^{2}} + \frac{1}{r}\,\frac{\mathrm{d} c^{(1)}}{\mathrm{d} r} - \frac{c^{(1)}}{r^{2}} = {\textit{Pe}}\, a_0\,\textit{Da} \, U_1 \left(\frac{1}{r^{3}}-\frac{1}{r}\right), \end{equation}

together with the matching condition (cf. (8.4))

(8.18)\begin{equation} c^{(1)} \sim \tfrac{1}{2}\textit{Pe} \,U_1 a_0\,\textit{Da} \left(\ln\frac{4}{\epsilon\,\textit{Pe}\,|U_1|\,r}- \gamma\right) r \quad \text{as} \ r\to\infty, \end{equation}

and the boundary condition (cf. (8.12))

(8.19)\begin{equation} \frac{\mathrm{d} c^{(1)}}{\mathrm{d} r}-\textit{Da}\, c^{(1)} = \textit{Da} \,a_0\,f^{(1)} \quad \text{at} \ r=1.\end{equation}

Note that (5.3a) and (8.14) imply that $f^{(1)}>0$.

The most general solution of (8.17) and (8.18) is

(8.20)\begin{align} c^{(1)} ={-}\tfrac{1}{2} \textit{Pe} \,a_0\,\textit{Da} \,U_1 \left( \frac{1}{r}+r\right) \ln r + \tfrac{1}{2}\textit{Pe} \, a_0\,\textit{Da}\, U_1 \left(\ln\frac{4}{\epsilon\,\textit{Pe}\,|U_1|}- \gamma\right) r + \frac{N_1}{r}. \end{align}

The coefficient $N_1$ is obtained readily from (8.19). It then follows that

(8.21)\begin{equation} c^{(1)}(1) = \frac{a_0\,\textit{Da}}{1+\textit{Da}} \left[ \textit{Pe}\,U_1\left(\ln\frac{4}{\epsilon\,\textit{Pe}\,|U_1|}- \gamma-1\right)-f^{(1)}\right]. \end{equation}

Substitution into (8.16) eventually gives, upon making use of (7.9) and (8.14),

(8.22)\begin{align} &U_1 \left[ \textit{Da}\,(2+2\textit{Da}+M\,\textit{Pe})\left(\ln\frac{4}{\epsilon\,\textit{Pe}\,|U_1|}- \gamma\right) +\textit{Da}\,(2-M\,\textit{Pe})+2\right] \nonumber\\ &\quad = \frac{2M\,\textit{Da}}{\rm \pi} \int_0^{\rm \pi} f(\theta)\cos \theta\, \mathrm{d}\theta. \end{align}

The implicit equation (8.22) provides $U_1$ as a function of the governing four parameters. The appearance of $\ln \epsilon$ results in a non-analytic dependence upon $\epsilon$ at $\epsilon =0$, as was to be expected from the singular nature of the limit $\epsilon \to 0$.

9. The limits of slow and fast kinetics

By replacing $U_1$ with $U/\epsilon$ in (8.22) and making use of (5.1), we obtain an implicit equation for $U$ itself:

(9.1)\begin{align} &U \left[ \textit{Da}\,(2+2\textit{Da}+M\,\textit{Pe})\left(\ln\frac{4}{\textit{Pe}\,|U|}- \gamma\right) +\textit{Da}\,(2-M\,\textit{Pe})+2\right] \nonumber\\ &\quad = \frac{2 M\,\textit{Da}}{\rm \pi} \int_0^{\rm \pi} F(\theta)\cos \theta\, \mathrm{d}\theta, \end{align}

with an asymptotic error that is algebraically small in $\epsilon$. Note that the dependence upon $\epsilon$ has disappeared; this was to be expected, as this parameter is not required for the problem specification.

When $\textit {Da}$ becomes small, we find from (9.1) the approximation

(9.2)\begin{equation} U \sim \frac{M\,\textit{Da}}{\rm \pi}\int_0^{\rm \pi} F(\theta)\cos \theta\, \mathrm{d}\theta, \end{equation}

which is no longer singular at $U=0$. In the other limit, as $\textit {Da}\to \infty$, we obtain

(9.3)\begin{equation} U \left(\ln\frac{4}{\textit{Pe}\,|U|}- \gamma\right) \sim \frac{M}{{\rm \pi}\,\textit{Da}} \int_0^{\rm \pi} F(\theta)\cos \theta\, \mathrm{d}\theta, \end{equation}

which essentially implies an $\operatorname {ord}(\textit {Da}^{-1})$ scaling of $U$. To understand the above limits, it is expedient to consider the limits $\textit {Da}\ll 1$ and $\textit {Da}\gg 1$ from the outset, allowing for $\epsilon$ to attain $\operatorname {ord}(1)$ values (subject to both (5.2) and (5.5)). It therefore proves useful to employ the original problem formulation, in terms of $F(\theta )$.

We start with the small-$\textit {Da}$ limit. With interfacial reaction being $\operatorname {ord}(\textit {Da})$ weak, it results in an $\operatorname {ord}(\textit {Da})$ perturbation to the unity equilibrium concentration specified by (3.2). The slip condition (3.7) then implies that the velocity field is $\operatorname {ord}(\textit {Da})$ small too, as is $U$ itself. Writing $c= 1 + \textit {Da}\,\tilde {c}$, we find that at leading order $\tilde {c}$ satisfies Laplace's equation in the vicinity of the disc, together with the Neumann condition (cf. (3.3))

(9.4)\begin{equation} \frac{\partial \tilde{c}}{\partial r} = F(\theta) \quad \text{at} \ r=1. \end{equation}

The solution that is least divergent as $r\to \infty$ is

(9.5)\begin{equation} \tilde{c} = \tilde{a} + \ln r - \frac{2}{\rm \pi} \sum_{n=1}^{\infty} \frac{\cos n\theta}{nr^{n}} \int_0^{\rm \pi} F(\vartheta) \cos n \vartheta \, \mathrm{d} \vartheta. \end{equation}

The constant $\tilde {a}$ cannot be determined from the analysis in the particle vicinity. Rather, it may be obtained by asymptotic matching with the leading-order approximation for $\tilde {c}$ in a remote region, which is now at distances $\operatorname {ord}(\textit {Da}^{-1})$. (This matching procedure excludes terms diverging like $r$ and faster in (9.5).) However, this constant is irrelevant to the calculation of the particle velocity. Thus, writing $U= \textit {Da}\,\tilde U$, we obtain readily from (3.9) that

(9.6)\begin{equation} \tilde U = \frac{M}{\rm \pi} \int_0^{\rm \pi} F(\theta) \cos \theta \, \mathrm{d} \theta, \end{equation}

in agreement with (9.2). With the remote region being irrelevant, it is hardly surprising that approximation (9.2) is independent of $\textit {Pe}$. While the original problem is ill-posed for $\textit {Da}=0$, it appears as though the singularity in the limit $\textit {Da}\to 0$ is a ‘removable’ one.

Consider now the limit $\textit {Da}\gg 1$. It is evident from condition (3.3) that $c$ possesses the generalised Poincaré expansion

(9.7)\begin{equation} c(r,\theta;\textit{Da}) = c_0(r,\theta;\textit{Da}) + \textit{Da}^{{-}1}\,c_1(r,\theta;\textit{Da}) + \cdots, \end{equation}

where $c_0$ satisfies the homogeneous Dirichlet condition

(9.8)\begin{equation} c_0 = 0 \quad \text{at} \ r=1. \end{equation}

With $c_0$ uniform at $r=1$, there is no slip to drive $\operatorname {ord}(1)$ fluid velocity, so we anticipate that $\boldsymbol {u}=\operatorname {ord}(\textit {Da}^{-1})$. The leading-order concentration then satisfies Laplace’s equation. Seeking the solution that diverges least rapidly at large $r$, we obtain

(9.9)\begin{equation} c_0 = a_0 \ln r. \end{equation}

The constant $a_0$ is determined from matching with a remote-region solution, now at distances $\textit {Da}^{-1}$. Writing $U= \textit {Da}^{-1}\,U_1 + \cdots$ and repeating an analysis similar to that in § 7 we find that (cf. (7.9))

(9.10)\begin{equation} a_0 =\left( \ln\frac{4\,\textit{Da}}{\textit{Pe}\,|U_1|}- \gamma \right)^{{-}1}. \end{equation}

At $\operatorname {ord}(1)$, we now find from (3.3) that

(9.11)\begin{equation} c_1 = \frac{a_0}{F(\theta)} \quad \text{at} \ r=1. \end{equation}

Substituting into (3.9) then gives

(9.12)\begin{equation} U_1 ={-}\frac{a_0 M}{\rm \pi}\int_{0}^{\rm \pi} \frac{F'(\theta)}{F^{2}(\theta)} \sin\theta \, \mathrm{d} \theta. \end{equation}

Introducing $f$ via (5.1) and forming the small-$\epsilon$ limit yields

(9.13)\begin{equation} U_1 \sim{-}\frac{\epsilon a_0 M}{\rm \pi}\int_{0}^{\rm \pi} f'(\theta) \sin\theta \, \mathrm{d} \theta. \end{equation}

Upon using (9.10) and the Fourier expansion (8.13)–(8.14), we finally obtain

(9.14)\begin{equation} U_1 \left( \ln\frac{4\,\textit{Da}}{\textit{Pe}\,|U_1|}- \gamma \right)\sim \frac{\epsilon M}{\rm \pi} \int_0^{\rm \pi} f(\theta)\cos \theta\, \mathrm{d}\theta. \end{equation}

Reverting to $U$ and $F$, we then retrieve (9.3).

The preceding analyses clarify why $U$ becomes small for both small and large $\textit {Da}$. For small $\textit {Da}$, the interfacial reaction is so slow that $c$ deviates only by $\operatorname {ord}(\textit {Da})$ values from the unity equilibrium values. These deviations result in an $\operatorname {ord}(\textit {Da})$ particle speed. For large $\textit {Da}$, the reaction is so fast that $c$ nearly vanishes at the interface, reducing there to $\operatorname {ord}(1/\textit {Da})$ values (up to logarithmic terms). Since it is the interfacial distribution that determines the particle speed (recall (3.9)), we again find that $U$ is small, now essentially $\operatorname {ord}(1/\textit {Da})$. For fixed $\epsilon$ and $\textit {Pe}$, both limits are associated with weak advection.

10. Dependence upon $M$

We now address the validity of (3.15) and (3.16). In the limits $\textit {Da}\ll 1$ and $\textit {Da}\gg 1$, we observe from (9.2) and (9.3) that $U$ satisfies (3.16). This proportionality does not apply, however, in the general case: indeed, it is verified readily from (8.22) that $U_1$ is not an odd function of $M$. This is hardly surprising: a non-trivial dependence upon $M$ was already observed by Michelin & Lauga (Reference Michelin and Lauga2014), who analysed self-propulsion in three dimensions at finite $\textit {Pe}$. The dependence upon $M$ in the present problem is illustrated in figure 2, where the product $MU_1$ is portrayed, for both $M=1$ and $M=-1$, as a function of $\textit {Da}$ for $\textit {Pe}=1$ and $\epsilon = 0.1$, using the distribution (5.7).

Figure 2. Variation of $MU_1$ with $\textit {Da}$ for $\textit {Pe}=1$ and $\epsilon = 0.1$, using the distribution (5.7). The solid curves are obtained from the implicit equation (9.1). The dashed curves show the small-$\textit {Da}$ approximation (9.2) and the large-$\textit {Da}$ approximation (9.3).

Having found that $U$ does not satisfy (3.16), we now address the weaker version (3.15). With the logarithmic expression $\ln (4/\epsilon \,\textit {Pe}\,|U_1|)$ being asymptotically large and positive for $\epsilon \ll 1$, it is evident that $U_1>0$ for $M=1$, in agreement with (3.15). For $M=-1$, the situation is more delicate. Assuming again that the logarithmic expression is large and positive, we find that $U_1<0$ for $\textit {Pe}$ that is smaller than $2+2\textit {Da}$. For $\textit {Pe} = 2+2\textit {Da}$, the term multiplying the logarithmic expression vanishes, and we find the closed-form solution

(10.1)\begin{equation} U_1={-}\frac{\textit{Da}}{{\rm \pi}(\textit{Da}+1)^{2}} \int_0^{\rm \pi} f(\theta)\cos \theta\, \mathrm{d}\theta < 0. \end{equation}

For $\textit {Pe}$ larger than $2+2\textit {Da}$, however, the term multiplying the logarithmic expression becomes negative, suggesting in turn a positive $U_1$.

To understand the possibility for a velocity reversal, we assess the critical value of $\textit {Pe}$ at which the expression within the brackets appearing in the left-hand side of (8.22) would vanish approximately. Towards this end, we temporarily abandon our generalised asymptotic approach, where logarithmically large terms are considered on a par with $\operatorname {ord}(1)$ terms, and consider an expansion of that expression in inverse powers of $\ln (1/\epsilon )$. In performing that expansion, we take the difference between the critical value $\textit {Pe}_\text {c}$ and $2+2\textit {Da}$ to be of order $1/\ln (1/\epsilon )$. Thus writing

(10.2)\begin{equation} \textit{Pe}_\text{c} = 2+2\textit{Da} + \frac{\varDelta}{\ln(1/\epsilon)}, \end{equation}

with $\varDelta$ being $\operatorname {ord}(1)$, we find that at $\operatorname {ord}(1)$ the expression within the brackets becomes

(10.3)\begin{equation} {-}\textit{Da}\,\varDelta + \textit{Da}(4+2\textit{Da}) + 2, \end{equation}

which vanishes for

(10.4)\begin{equation} \varDelta = 2\,\frac{(\textit{Da}+1)^{2}}{\textit{Da}}. \end{equation}

The above analysis may appear to suggest a transition from negative to positive $U_1$ at a critical value at which the expression within the brackets appearing in the left-hand side of (8.22) vanishes, giving rise to a diverging $U_1$. This is, however, only a crude estimate: as the expression within the brackets approaches zero, $U_1$ (which is negative) becomes large, and the above balance becomes invalidated due to the $\ln |U_1|$ term in the brackets. The numerical solution of (8.22) for $M=-1$ actually reveals that a bifurcation occurs at a critical value of $\textit {Pe}$, where two positive solutions appear. This is illustrated in figure 3, where we portray the velocity $U_1$ as a function of $\textit {Pe}$ for $\epsilon =0.1$ and $\textit {Da}=1$, using the distribution (5.7). At these values, the bifurcation appears at $\textit {Pe}\approx 17.3$. We conclude that (3.15) is invalid.

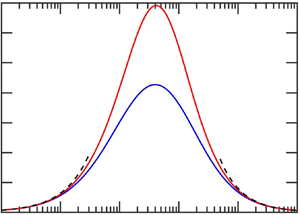
Figure 3. Variation of $U_1$ with $\textit {Pe}$ for $M=-1$, $\textit {Da}=1$ and $\epsilon = 0.1$, using the distribution (5.7). We show both the negative branch and the multi-valued positive branch, which exists for $\textit {Pe}>\textit {Pe}_{c}$.

11. Concluding remarks

We have analysed the phoretic self-propulsion of a circular disc whose interfacial activity is slightly inhomogeneous. The analysis was based upon a linearisation scheme that exploited the slight inhomogeneity. This scheme implies that advection is relatively weak even for $\operatorname {ord}(1)$ values of the intrinsic Péclet number $\textit {Pe}$. The dominance of diffusion over advection is not uniformly valid. The analysis of this singular limit requires the use of matched asymptotic expansions. As is customary in singular problems in two dimensions (Frankel & Acrivos Reference Frankel and Acrivos1968), we have employed generalised Poincaré expansions, allowing for a logarithmic dependence of the various asymptotic orders upon the expansion parameter $\epsilon$. This has allowed for a straightforward use of the Van Dyke matching rule.

Our key result is (9.1), which provides, for a given distribution of interfacial reaction rate, the dimensionless velocity of the particle as an implicit function of the slip sign $M$, the intrinsic Péclet number $\textit {Pe}$, and the Damköhler number $\textit {Da}$. The functional dependence upon $M$ is non-trivial, with a possibility of velocity reversal existing for $M=-1$. We have also obtained simpler approximations in the limits of small and large $\textit {Da}$, which are not restricted by the assumption $\epsilon \ll 1$.

The velocity reversal appearing for $M=-1$ beyond a critical value of $\textit {Pe}$ brings to mind the possibility of spontaneous motion at finite $\textit {Pe}$. This possibility was investigated in detail in three dimensions, using the highly symmetric configuration discussed in § 1. Thus Michelin et al. (Reference Michelin, Lauga and Bartolo2013) observed that in addition to the ‘trivial’ quiescent solution, with a stationary particle, the governing equations also admit a non-trivial solution beyond a critical value of $\textit {Pe}$; this solution corresponds to self-sustained motion. For an absorbing boundary (in tune with (3.3)), such spontaneous motion can take place only for $M=-1$. Recently, Saha et al. (Reference Saha, Yariv and Schnitzer2021) studied the linearised response of the same system to a weak external force and found a bifurcation at the same critical value. In fact, it was shown by Saha et al. (Reference Saha, Yariv and Schnitzer2021) that the study of the forced problem provides a convenient alternative to the stability analysis of the unforced problem.

Can spontaneous motion also occur in two dimensions? This is a subtle question: with the reference state being ill-posed (Hu et al. Reference Hu, Lin, Rafai and Misbah2019), there is no two-dimensional counterpart to the stability analysis of Michelin et al. (Reference Michelin, Lauga and Bartolo2013). One can imagine investigating the weakly-forced problem, following Saha et al. (Reference Saha, Yariv and Schnitzer2021). In that problem, the advection triggered by the motion of the disc renders the solute-transport problem well-posed. Unfortunately, a forced problem cannot be studied under the framework of Stokes equations in two dimensions, due to the Stokes paradox. We propose that the present analysis, where the highly symmetric configuration is perturbed by a weak inhomogeneity, may provide a first step in the right direction. Indeed, the bifurcation of $U_1$ at a critical value of $\textit {Pe}$, which approaches $2+2\textit {Da}$ as $\epsilon \to 0$, may be a signature of spontaneous motion.

Finally, it is illuminating to provide here the dimensional counterpart of (9.1), namely

(11.1)\begin{align} &s \left[ \frac{a\bar{k}}{D}\left(2 +2\,\frac{a\bar{k}}{D} + \frac{bc_\infty}{D}\right) \left(\ln\frac{4D}{ a\,|s|}-\gamma\right) + \frac{a\bar{k}}{D}\left(2-\frac{bc_\infty}{D}\right)+2\right] \nonumber\\ &\quad = \frac{2bc_\infty}{{\rm \pi} D}\int_0^{\rm \pi} k(\theta)\cos \theta\, \mathrm{d}\theta. \end{align}

Note the appearance of two Péclet numbers. The first, $bc_\infty /a$, is the signed version of the Péclet number $\textit {Pe}$ used in the dimensionless analysis. The second, $a\,|s|/D$, is the number associated with the particle speed. While our analysis is valid provided that the latter number is small, we anticipate that (11.1) may provide a rough approximation even when this restriction is violated.