1. Introduction
Oceanic flows are comprised of a vast range of spatio-temporal scales, but global ocean models only partially resolve this rich range of scales due to limited computational power (e.g. Fox-Kemper et al. Reference Fox-Kemper2019). Relatedly, their results have been shown to depend sensitively on how the subgrid-scale mixing of scalars and momentum are modelled (e.g. Bryan Reference Bryan1987; Jayne Reference Jayne2009), and in particular, great effort has been devoted to the accurate representation of the subgrid-scale vertical buoyancy flux because of its impact on the background density field as well as on the global ocean circulation through the buoyancy force (de Lavergne et al. Reference de Lavergne, Madec, Le Sommer, Nurser and Naveira Garabato2015; Mashayek et al. Reference Mashayek, Salehipour, Bouffard, Caulfield, Ferrari, Nikurashin, Peltier and Smyth2017; Cimoli et al. Reference Cimoli, Caulfield, Johnson, Marshall, Mashayek, Naveira Garabato and Vic2019). The down-gradient model introduced by Osborn (Reference Osborn1980) has been widely used to represent the subgrid-scale vertical buoyancy flux in global ocean models, and a non-dimensional form of this model from Salehipour & Peltier (Reference Salehipour and Peltier2015) is provided below
\begin{equation} \frac{D_{T}}{D} = \left( \frac{Ri_{f}}{1 - Ri_{f}} \right) \frac{\epsilon_{k}}{D N^{2}} = \varGamma \left( \frac{\epsilon_{k}}{\nu N^{2}} \right) \left( \frac{\nu}{D} \right) = \varGamma Re_{b} Pr. \end{equation}
In (1.1), 
$D$ and 
$D_T$ are the molecular and eddy diffusivities of density, 
$\nu$ is the kinematic viscosity of the fluid, 
$N^2$ is the vertical background stratification, 
$\epsilon _k$ is the rate of turbulent kinetic energy (TKE) dissipation, 
$Ri_f$ is the flux Richardson number or mixing efficiency, 
$\varGamma = Ri_f / (1-Ri_f )$ is the mixing coefficient, 
$Re_b = \epsilon _k / (\nu N^2 )$ is the buoyancy Reynolds number and 
$Pr = \nu / D$ is the molecular Prandtl number.
By combining microstructure measurements of 
$\epsilon _k$, conductivity-temperature-depth-based (CTD)-based measurements of 
$N^2$ and known values of 
$\nu$ and 
$D$, it is possible to estimate 
$Re_b$ and 
$Pr$. Then, the final challenge with applying (1.1) to estimate the eddy diffusivity is quantifying 
$\varGamma$ in terms of easily measurable and known quantities. There has been extensive research and discussion surrounding (1.1), and comprehensive summaries are provided in the review articles of Ivey, Winters & Koseff (Reference Ivey, Winters and Koseff2008), Gregg et al. (Reference Gregg, D'Asaro, Riley and Kunze2018) and Caulfield (Reference Caulfield2020, Reference Caulfield2021). Recently, one notable advancement has been provided by Maffioli, Brethouwer & Lindborg (Reference Maffioli, Brethouwer and Lindborg2016), who showed that 
$\varGamma$ depends primarily on the turbulent Froude number (
$Fr$) and not the buoyancy Reynolds number (
$Re_b$). The turbulent Froude number can be interpreted as a ratio of the buoyancy and eddy turnover time scales, and the buoyancy Reynolds number can be interpreted as the square of the ratio of the buoyancy and dissipation/Kolmogorov time scales. Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) showed that 
$\varGamma \sim Fr^{-2}$ for weak stratification (
$Fr \gg 1$) and 
$\varGamma \approx \text{const.}$ for strong stratification (
$Fr \ll 1$), and hypothesized that the non-unique relationships of 
$\varGamma = f ( Re_b )$ (e.g. figure 2 of Monismith, Koseff & White Reference Monismith, Koseff and White2018) would be addressed when considering 
$\varGamma = g ( Fr )$ (e.g. figures 14 and 6 of Issaev et al. Reference Issaev, Williamson, Armfield and Norris2022). Subsequently, Garanaik & Venayagamoorthy (Reference Garanaik and Venayagamoorthy2019) provided theoretical arguments for the relationships between 
$\varGamma$ and 
$Fr$, where they introduced a third scaling regime for moderate stratification 
$( Fr \sim {O} ( 1 ) )$ with 
$\varGamma \sim Fr^{-1}$. They tested these scaling relationships for 
$\varGamma$ using three different direct numerical simulation (DNS) datasets of homogeneous stably stratified turbulence: (i) decaying simulations of Garanaik & Venayagamoorthy (Reference Garanaik and Venayagamoorthy2018); (ii) forced simulations of Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016); (iii) sheared simulations of Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005). The decaying and forced simulations exhibited great agreement with their theoretical scaling regimes. Nevertheless, the sheared dataset of Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005) did not visually exhibit the same degree of agreement with the scaling as a function of 
$Fr$ as the two unsheared datasets (see figure 1 of Garanaik & Venayagamoorthy Reference Garanaik and Venayagamoorthy2019).
To better understand this discrepancy between the mixing coefficient scaling relationships for unsheared and sheared, stably stratified turbulence, we revisit the theoretical arguments of Garanaik & Venayagamoorthy (Reference Garanaik and Venayagamoorthy2019), hereafter referred to as GV. Specifically, for flows where the shear time scale 
$\tau _S \sim 1/S$ is faster than the buoyancy time scale 
$\tau _B \sim 1/N$, we introduce modifications to the GV scaling such that 
$\varGamma$ depends on both the non-dimensional shear parameter 
$S_\ast = S k/\epsilon _k$ and the turbulent Froude number 
$Fr_k= \epsilon _k / ( Nk )$, where 
$\tau _L \sim k/\epsilon _k$ is the large-eddy time scale. We then validate our revised scaling relationships using two independent datasets of homogeneous, sheared, stably stratified, turbulence (one dataset from Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005); another dataset generated based on equations and methods outlined in § 3). We note that Mater & Venayagamoorthy (Reference Mater and Venayagamoorthy2014a,Reference Mater and Venayagamoorthyb) have also explored a two-parameter description of stably stratified turbulence using the two variables, 
$S \tau _L \sim S_\ast$ and 
$N \tau _L \sim 1/Fr_k$.
Our paper is organized as follows. In § 2, we provide an overview of the GV scaling procedure and introduce modifications to account for mean shear. In § 3, we introduce the equations of motion and describe the solution methods that were used to generate a second database of homogeneous, sheared, stably stratified turbulence and compare the resulting turbulence of this new shear-forced model problem with homogeneous shear flows. In § 4, we test and validate our revised scaling using two DNS datasets of homogeneous, sheared, stably stratified turbulence (one by Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005); another described in § 3), and test the applicability of our revised scaling for more complex sheared, stably stratified turbulent flows using two additional datasets (DNS of spatio-temporally evolving, radiatively heated, stably stratified, open channel flow by Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022); field measurements of stably stratified atmospheric boundary-layer turbulence studied by Conry, Kit & Fernando Reference Conry, Kit and Fernando2020). We also explore the relationship between our revised scaling regimes and existing descriptions of the mixing efficiency based on the gradient Richardson number and briefly examine the effects of finite Reynolds number of the simulations on the mixing efficiency. In § 5, we close with a few concluding remarks.
2. Original and revised GV scaling arguments
2.1. Recap of the GV mixing coefficient scaling relationships
Before considering the effects of mean shear, we first summarize the turbulent Froude number (
$Fr_k$) scaling relationships for the mixing coefficient (
$\varGamma$) from Garanaik & Venayagamoorthy (Reference Garanaik and Venayagamoorthy2019) (see table 1 for a summary of the GV scaling). Given the Osborn eddy diffusivity model for the vertical buoyancy flux (1.1), the GV scaling procedure seeks to model the mixing coefficient 
$\varGamma = B / \epsilon _k$ for three regimes of stably stratified turbulence: (i) weak stratification (
$Fr_k > 1$), (ii) moderate stratification (
$Fr_k \sim {O}( 1 )$) and (iii) strong stratification (
$Fr_k < 1$). Here, we use 
$Fr_k = \epsilon _k/( Nk )$ rather than 
$Fr = \epsilon _k / ( N u_{rms}^2 )$, where 
$k$ represents the TKE, and 
$u_{{rms}}$ represents the root-mean-square horizontal velocity fluctuations, to be consistent with the presentation of GV. When stratification increases, leading to increasingly damped vertical velocity fluctuations, we expect 
$Fr_k$ and 
$Fr$ to become similar in magnitude. For forced, axisymmetric, strongly stratified turbulence, 
$k = ( u^2+v^2+w^2 )/2 \approx ( u^2+v^2 )/2 \approx u_{rms}^2$ (i.e. 
$Fr_{k} \approx Fr$), and for sheared, strongly stratified turbulence, 
$k = ( u^2+v^2+w^2 ) / 2 \approx u^2 / 2 \approx u_{rms}^2/2$ (i.e. 
$Fr_{k} \approx 2Fr$). In these expressions, 
$u$, 
$v$ and 
$w$ represent velocity fluctuations in the 
$x$-, 
$y$- and 
$z$-directions, respectively, with gravity acting in the 
$z$-direction.
Table 1. GV scaling for unsheared stably stratified turbulence.
The GV scaling estimates the vertical displacement of fluid parcels as 
$l_z \sim w \tau _1$, where 
$w$ represents the vertical velocity fluctuations, and 
$\tau _1$ represents a time scale connecting the vertical velocity fluctuations to the vertical displacement of fluid parcels. Next, the TKE dissipation rate is scaled as 
$\epsilon _k \sim w^2/\tau _2$, where 
$\tau _2$ represents a time scale connecting the vertical component of the TKE to the TKE dissipation rate. Using the first scaling, density fluctuations are scaled as 
$\rho \sim l_z d_z \bar {\rho } \sim w \tau _1 d_z\bar {\rho }$, and substituting this into the vertical buoyancy flux expression leads to 
$B = ( g / \rho _0 ) \overline {w \rho } \sim w^2 N^2 \tau _1$, where 
$N^2 = -(g / \rho _0 ) d_z\bar {\rho }$ is the background vertical stratification. Combining the scaling for 
$B$ and 
$\epsilon _k$, the GV scaling for the mixing coefficient can be generally stated as
\begin{equation} \varGamma=\frac{B}{\epsilon_k}\sim N^2\tau_1\tau_2, \end{equation}
where now physically appropriate 
$\tau _1$ and 
$\tau _2$ can be chosen for the three stably stratified turbulence regimes of interest. For weakly stratified turbulence, 
$\tau _1 \sim \tau _2 \sim \tau _L$. This leads to 
$\varGamma \sim ( N \tau _L )^2 \sim Fr_k^{-2}$. For moderately stratified turbulence, the buoyancy time scale and large-eddy time scale have comparable magnitudes, so GV pick 
$\tau _1 \sim \tau _B$ and 
$\tau _2 \sim \tau _L$ to incorporate both time scales, resulting in 
$\varGamma \sim N \tau _L \sim Fr_k^{-1}$. For strongly stratified turbulence, 
$\tau _1 \sim \tau _2 \sim \tau _B$, which leads to 
$\varGamma \sim Fr_k^0 \approx \text {const}$.
There are three alternatives for scaling the moderately stratified regime, which are not explicitly discussed by Garanaik & Venayagamoorthy (Reference Garanaik and Venayagamoorthy2019). These alternatives arise because 
$\tau _L \sim \tau _B$ for 
$Fr_k \sim {O} ( 1 )$. First, we could have chosen 
$\tau _1 \sim \tau _L$ and 
$\tau _2 \sim \tau _B$. This also leads to 
$\varGamma \sim Fr_k^{-1}$, but based solely on scaling arguments, it cannot be distinguished from the choice made by GV. Second, we could have chosen 
$\tau _1 \sim \tau _2 \sim \tau _L$ and arrived at 
$\varGamma \sim Fr_k^{-2}$ as with the weakly stratified regime. Third, we could have chosen 
$\tau _1 \sim \tau _2 \sim \tau _B$ and arrived at 
$\varGamma \sim Fr_k^0 \approx \text {const.}$ as with the strongly stratified regime. We interpret this ambiguity as a consequence of this regime being a transition zone between weakly stratified and strongly stratified regimes, which is how this regime is described by Garanaik & Venayagamoorthy (Reference Garanaik and Venayagamoorthy2019).
2.2. Revised mixing coefficient scaling relationships with mean shear
Extending the scaling arguments of GV to flows with mean shear requires taking note of a third time scale 
$\tau _S \sim 1/S$, where 
$S$ is the magnitude of the mean shear, and 
$\tau _S$ is the shear time scale (see table 2 for a summary of our revised scaling relationships). Before proceeding, we impose two restrictions to limit the flows of interest. First, we limit our consideration to flows with vertically sheared, mean horizontal velocities (i.e. turbulence involving 
$\partial _z \bar {u}$ and 
$\partial _z \bar {v}$) such that 
$S^2={(\partial _z \bar {u})}^2 + {(\partial _z \bar {v})}^2$. Furthermore, we only choose to consider flows with minimal temporal variations of 
$S$ and 
$N^2$. For flows with non-negligible temporal variations of 
$S$ and 
$N^2$ (e.g. Kirkpatrick et al. Reference Kirkpatrick, Williamson, Armfield and Zecevic2019, Reference Kirkpatrick, Williamson, Armfield and Zecevic2020; Onuki, Joubaud & Dauxois Reference Onuki, Joubaud and Dauxois2021; Issaev et al. Reference Issaev, Williamson, Armfield and Norris2022), we would need to account for two additional time scales associated with 
$\partial _t S$ and 
$\partial _t N^2$ for a total of five physical time scales (or four non-dimensional parameters) when estimating 
$\varGamma$ using (2.1). In the following discussion, we take the simplest limit of vertically sheared, stably stratified turbulence where 
$\partial _t N^2 = \partial _t S = 0$, which is true for homogeneous problems where 
$N^2$ and 
$S$ are uniform in space and constant in time.
Table 2. Revised scaling for sheared stably stratified turbulence.
For these simplest vertically sheared, stably stratified turbulent flows, we only need to compare the magnitude of 
$\tau _S$ with 
$\tau _L$ and 
$\tau _B$ to decide how the shear time scale should factor into (2.1). To proceed, we can combine the three time scales as
\begin{gather} S_\ast = Sk/\epsilon_k\sim\tau_L/\tau_S, \end{gather}
\begin{gather}Ri_g = N^2/S^2\sim\left(\tau_S/\tau_B\right)^2, \end{gather}
where 
$S_\ast$ is the non-dimensional shear parameter, and 
$Ri_g$ is the gradient Richardson number. First, we note that 
$S_\ast > 1$ is typically observed for unstratified turbulent shear flows (e.g. tables 5.3 and 7.2 of Pope Reference Pope2000) as well as for stably stratified turbulent shear flows across a wide range of stratification strengths (e.g. Shih et al. Reference Shih, Koseff, Ferziger and Rehmann2000). Second, we restrict our scaling analysis to a shear-dominant regime where 
$Ri_g < 1$. Together, these two constraints lead to 
$\tau _S < \tau _L , \tau _B$, and therefore, we always incorporate 
$\tau _S$ as one of the two time scales in (2.1). For the remaining time scale in (2.1), we choose either 
$\tau _L$ for weakly stratified turbulence or 
$\tau _B$ for moderately stratified turbulence, following the original GV scaling arguments. Here, we have refrained from specifically attributing 
$\tau _S$ to either 
$\tau _1$ or 
$\tau _2$ to avoid the ambiguity we highlighted at the end of the previous section. With these choices, we find 
$\varGamma \sim Fr_k^{-2} S_{\ast }^{-1}$ for weakly stratified sheared turbulence, and 
$\varGamma \sim Fr_k^{-1}S_{\ast }^{-1}$ for moderately stratified sheared turbulence. The scaling process, however, is inconclusive for strongly stratified sheared turbulence, so we empirically explore this regime using two DNS datasets of homogeneous, sheared, stably stratified turbulence in § 4 and find 
$\varGamma \sim Fr_k^{-0.5}S_{\ast }^{-1}$. Once again, the GV and revised scaling arguments are summarized in tables 1 and 2, respectively.
Before ending this section, we would like to focus briefly on our assumption that 
$\partial _t N^2 = \partial _t S = 0$, which in fact technically excludes our revised scaling from applying to stably stratified shear layers. This is an important issue that needs to be addressed given that these flows are considered to be an appropriate model problem for the actual irreversible mixing occurring in Earth's oceans (e.g. Mashayek et al. Reference Mashayek, Salehipour, Bouffard, Caulfield, Ferrari, Nikurashin, Peltier and Smyth2017; Salehipour & Peltier Reference Salehipour and Peltier2019; Mashayek, Caulfield & Alford Reference Mashayek, Caulfield and Alford2021; Mashayek et al. Reference Mashayek, Baker, Cael and Caulfield2022). While there has been some success in describing 
$\varGamma$ from these flows as a function of 
$Fr$ (see figure 17 of VanDine, Pham & Sarkar Reference VanDine, Pham and Sarkar2021), it appears that 
$Fr$ alone is insufficient to fully characterize the behaviour of 
$\varGamma$ for this class of flows. For example, for forced stably stratified turbulence, Howland, Taylor & Caulfield (Reference Howland, Taylor and Caulfield2020) showed that 
$\varGamma$ could vary by roughly 
$30$ % at the same turbulent Froude number (
$Fr \approx 10^{-2}$), indicating that while the power-law exponent in 
$\varGamma \approx a Fr_{k}^{-\beta }$ can be estimated, the variations of the scaling coefficient 
$a$ need to be captured by an additional parameter. This type of sensitivity of 
$\varGamma$ to the turbulence generation mechanism has also been noted for stably stratified shear layers when contrasting the mixing properties of Kelvin–Helmholtz and Holmboe systems (Salehipour, Caulfield & Peltier Reference Salehipour, Caulfield and Peltier2016). This effect will be further pronounced for buoyancy-driven flows where very efficient mixing is expected (e.g. Davies Wykes, Hughes & Dalziel Reference Davies Wykes, Hughes and Dalziel2015; Bou-Zeid et al. Reference Bou-Zeid, Gao, Ansorge and Katul2018). Furthermore, as will be shown in § 4, our revised scaling seems to suggest that not only are the transition values of 
$Fr_{k}$ distinct between sheared and body-forced stably stratified turbulent flows, but that the power-law exponents predicted by the GV scaling need to be modified when shear is introduced into the system. Going back to the 
$\varGamma \approx a Fr_{k}^{-\beta }$ formulation, this implies that 
$Fr_{k}$ alone is insufficient for estimating the power-law exponent 
$\beta$ for sheared, stably stratified turbulence.
Given these points, we expect our revised scaling for sheared, stably stratified turbulence with constant mean shear and stratification to apply more broadly to even describe 
$\varGamma$ from stably stratified shear layers. How much our revised scaling needs to be modified to account for time-varying mean shear and stratification will depend on how quickly these two mean quantities evolve relative to the turbulence statistics. If they evolve slowly relative to the turbulence, then very minor (and possibly even no) modifications may be necessary. The fact that the GV scaling is successful at capturing the mixing dynamics of temporally decaying stably stratified turbulence provides further inkling that our revised scaling relationships could apply to a wider range of flows than we have explicitly proposed them for.
3. Shear-forced model problem
3.1. Equations of motion and solution methodology
To generate a second database of sheared, stably stratified turbulence, we studied the incompressible, Navier–Stokes equations under the Boussinesq approximation with a linear shear forcing (Dhandapani, Rah & Blanquart Reference Dhandapani, Rah and Blanquart2019)
\begin{gather} \frac{\partial u_{j}}{\partial x_{j}} = 0, \end{gather}
\begin{gather}\frac{\partial u_{j}}{\partial t} + u_{m} \frac{\partial u_{j}}{\partial x_{m}} ={-} \frac{1}{\rho_{0}} \frac{\partial p}{\partial x_{j}} - \frac{g}{\rho_{0}} \rho \delta_{j3} + \nu \frac{\partial^{2} u_{j}}{\partial x_{m} \partial x_{m}} -wS \delta_{j1}, \end{gather}
\begin{gather}\frac{\partial \rho}{\partial t} + u_{m} \frac{\partial \rho}{\partial x_{m}} + w \frac{{\rm d} \bar{\rho}}{{\rm d}z} = D \frac{\partial^{2} \rho}{\partial x_{m} \partial x_{m}}. \end{gather}
In (3.1)–(3.3), 
$u_j$, 
$p$, 
$\rho$ represent velocity, pressure and density fluctuations, respectively, 
$\bar {\rho } ( z )$ is the linearly varying, stable, background density field, 
$g$ is the gravitational acceleration, 
$\rho _0$ is the reference density, 
$\nu$ is the kinematic viscosity of the fluid, 
$D$ is the molecular diffusivity of density and 
$S$ is the forcing rate associated with the linear shear forcing. Tensor indices (
$1, 2, 3$) correspond to spatial directions (
$x, y, z$) and velocity fields (
$u, v, w$) with gravity acting along the 
$z$-axis.
Unlike classical homogeneous sheared turbulence, this particular system, which we will refer to as the shear-forced model problem, has no mean velocity field, but it does have the same right-hand side forcing term in (3.2) as its classical counterpart, which then leads to the same shear production term in the TKE equation. While (3.1)–(3.3) lead to identical volume-averaged turbulence budgets, there is a modified pre-factor in the Poisson equation for the pressure fluctuations, so the volume-averaged pressure-strain correlations and, consequently, the relative magnitudes of the Reynolds stresses differ from their classical counterparts (see tables 1 and 2 of Dhandapani et al. Reference Dhandapani, Rah and Blanquart2019). In § 3.2, we quantitatively compare the turbulence of the shear-forced model problem with that of stably stratified homogeneous shear flow from Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005).
We solved (3.1)–(3.3) for triply periodic domains (either cubic with length 
$L=2{\rm \pi}$ or rectangular with 
$L_x=4{\rm \pi}$ and 
$L_y=L_z=2{\rm \pi}$) using our own Fourier pseudospectral solver with an RK4 time-stepping scheme, where the rectangular domain simulations were conducted to explore domain-size effects. Global and simulation-specific parameters are provided in tables 3 and 4, respectively, where the quantities in columns 3–10 of table 4 are values calculated from volume and time averaging over the statistically stationary portions of each simulation. The fourth-order temporal accuracy and nonlinear advection terms were verified by comparing our numerical solutions with the analytical solutions of a decaying, two-dimensional, Taylor–Green vortex (Canuto et al. Reference Canuto, Quarteroni, Hussaini and Zang2007), and the nonlinear terms were dealiased exactly by zero padding (Canuto et al. Reference Canuto, Hussaini, Quarteroni and Zang2006). Finally, we implicitly verified the linear shear forcing and density coupling by considering the volume-averaged TKE (
$k=\overline {u_ju_j}/2$) and turbulent potential energy (TPE) (
$k_p=\alpha ^2\overline {\rho \rho }/2$) budgets associated with (3.1)–(3.3)
\begin{gather} \frac{{\rm d}k}{{\rm d}t} ={-}\overline{uw}S -\frac{g}{\rho_0} \overline{w\rho} -\nu\overline{ \frac{\partial u_j}{\partial x_m}\frac{\partial u_j}{\partial x_m}} = P_k - B - \epsilon_k, \end{gather}
\begin{gather}\frac{{\rm d}k_{p}}{{\rm d}t} =\frac{g}{\rho_0} \overline{w\rho} - D\alpha^2 \overline{\frac{\partial\rho}{\partial x_m}\frac{\partial\rho}{\partial x_m}} = B - \epsilon_p. \end{gather}
In (3.4) and (3.5), 
$\alpha =g / ( \rho _0 N )$ is a constant and uniform dimensional factor, which converts the dimensions of density to those of velocity, 
$P_k$ is the rate of production of TKE from the shear forcing, 
$B$ is the buoyancy flux and 
$\epsilon _k$ and 
$\epsilon _p$ are the dissipation rates of TKE and TPE, respectively. Subscripts 
$k$ and 
$p$ indicate quantities associated with TKE and TPE and do not indicate tensor indices.
Table 3. Global input parameters for the numerical simulations. Simulations C1–C6 and R16 (see table 4) used 
$\Delta t = 1.25\times 10^{-3}$ for numerical stability.
Table 4. Non-dimensional input and output parameters of interest for the Yi & Koseff (YK) dataset. For the columns with non-dimensional length scales, 
$L$ denotes the cubic domain length of 2
${\rm \pi}$, and 
$l_{O} = (\epsilon _{k}/N^{3})^{1/2}$, 
$l_{C} = (\epsilon _{k}/S^{3})^{1/2}$ and 
$\eta = (\nu ^{3}/\epsilon _{k})^{1/4}$ denote the Ozmidov, Corrsin and Kolmogorov length scales, respectively; 
$Re_{L} = k^{2}/(\nu \epsilon _{k})$, 
$Re_{b} = \epsilon _{k}/(\nu N^{2})$ and 
$Re_{S} = \epsilon _{k}/(\nu S^{2})$ represent the large-eddy, buoyancy and shear Reynolds numbers, respectively. For simulations R15, R16 and R18, time-averaged statistics have been calculated over multiple segments to avoid averaging over times when 
$Re_{b}$ was below a turbulence threshold, which we selected to be 
$Re_{b} =1$.
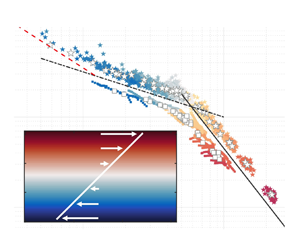
In figure 1(a,b) we plot the steady-state volume- and time-averaged TKE (3.4) and TPE (3.5) budgets as a function of the gradient Richardson number (
$Ri_g=N^2/S^2$) with all terms normalized such that they are bounded between 
${\pm }1$. Filled symbols represent values from the cubic domain simulations, and open symbols represent values from the rectangular domain simulations. For the TKE budget (figure 1a), we note that the production term (black triangles) accounts for all of the TKE generation at all values of 
$Ri_g$, while the sum of the buoyancy flux and TKE dissipation rate (orange stars and red triangles) account for the total loss of TKE. As 
$Ri_g$ increases, the buoyancy flux becomes an increasingly significant sink of TKE until 
$Ri_g = 1/4$, above which its relative magnitude remains unchanged until 
$Ri_g = 1$ where it diminishes in magnitude. Similar behaviour is noted for the TKE dissipation rate, where it becomes an increasingly less important sink of TKE until 
$Ri_g = 1/4$, above which its relative magnitude remains unchanged until 
$Ri_g = 1$ where it increases in magnitude. For the TPE budget (figure 1b), we observe that the buoyancy flux accounts for the total generation of TPE (orange stars), and the TPE dissipation rate (red triangles) accounts for the total loss of TPE. For both budgets, the residuals (grey squares) are near zero, indicating that our simulations are exhibiting the expected statistically stationary dynamics described by (3.4) and (3.5).
Figure 1. Steady-state volume- and time-averaged budgets of (a) TKE and (b) TPE as a function of the gradient Richardson number. The two panels correspond to (3.4) and (3.5), respectively. Filled symbols represent values from the cubic domain simulations, and open symbols represent values from the rectangular domain simulations. Given that the residuals of the volume- and time-averaged TKE and TPE budgets are near zero (grey squares in panels a,b), we take this as a verification that our numerical solver is accurately solving (3.1)–(3.3).
3.2. Comparison of shear-forced model problem with homogeneous shear flow
To quantitatively characterize the differences between the stably stratified, homogeneous shear flow considered in Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005) (SKIF) and the shear-forced model problem introduced in § 3.1 (YK), we plot 
$b_{13}$, 
$S_{*}$, 
$Fr_{k}$ as a function of 
$Ri_{g}$ for the SKIF and YK datasets with 
$Re_{b} = \epsilon _{k}/(\nu N^{2})$ in colour. Here, 
$b_{13}$ is the 
$i=1$, 
$j=3$ entry of the normalized Reynolds-stress anisotropy tensor 
$b_{ij} = \overline {u_i u_j} / ( 2k ) - (1/3 ) \delta _{ij}$. The horizontal dashed lines in panels (a,b) indicate typical ranges of 
$b_{13}$ and 
$S_{*}$ that have been observed in experiments and simulations of homogeneous shear flows under neutral conditions (values are from table 2 of Kasbaoui et al. Reference Kasbaoui, Patel, Koch and Desjardins2017), and the dashed-dotted line in panel (b) indicates 
$S_{*} = 5.5$ (or 
$Sq^{2}/\epsilon _{k} = 11$), which is the late-time, asymptotic value approached by the three DNS runs of Kasbaoui et al. (Reference Kasbaoui, Patel, Koch and Desjardins2017). There are some notable differences between the two flows as shown in these plots. First, the SKIF and YK datasets exhibit different values of 
$b_{13}$ at similar values of 
$Ri_{g}$ and 
$Re_{b}$, and the 
$b_{13}$ values from the YK dataset only begins to fall within the typical range for cases with strong stratification when 
$Ri_{g} > 0.3$. For weak stratification (
$Ri_{g} < 0.1$), the SKIF dataset exhibits 
$b_{13} \approx -0.15$, and the YK dataset exhibits 
$b_{13} \approx -0.2$. Second, regarding 
$S_{*}$, the SKIF dataset exhibits values between 
$4$ and 
$6$ across a wide range of 
$Ri_{g}$. The YK dataset, however, exhibits 
$S_{*} \approx 2$ for 
$Ri_{g} < 0.1$, which then also increases monotonically with increasing 
$Ri_{g}$. Finally, the SKIF and YK datasets also exhibit different values of 
$Fr_{k}$ at similar values of 
$Ri_{g}$ and 
$Re_{b}$, but this difference largely disappears for 
$Ri_{g} > 0.2$.
Another way to compare the turbulence characteristics of the SKIF and YK datasets is by considering (3.4) and (3.5) under statistically stationary conditions. Doing so leads to either of the following relationships:
\begin{equation} S_{*} ={-}\frac{\left(1 + \varGamma \right)}{2 b_{13}}, \quad \frac{N}{S}={-}\frac{2b_{13}}{Fr_k\left(1+\varGamma\right)}, \end{equation}
which can be related to the growth rate of the TKE (e.g. Holt, Koseff & Ferziger Reference Holt, Koseff and Ferziger1992; Jacobitz, Sarkar & Van Atta Reference Jacobitz, Sarkar and Van Atta1997; Shih et al. Reference Shih, Koseff, Ferziger and Rehmann2000). In (3.6a,b), 
$\varGamma = \epsilon _p / \epsilon _k$ is the irreversible mixing coefficient. The first expression has been considered by Shih et al. (Reference Shih, Koseff, Ferziger and Rehmann2000) for stably stratified, homogeneous shear flow, which broadly exhibits transient growth or decay depending on the sign of the sum of the right-hand side terms in (3.4). Over a narrow range of Reynolds and Richardson numbers, however, the turbulence reaches statistically stationary states (e.g. see figure 10 of Shih et al. (Reference Shih, Koseff, Ferziger and Rehmann2000) and also Portwood, de Bruyn Kops & Caulfield Reference Portwood, de Bruyn Kops and Caulfield2019). The second expression is closely related to the first, but it connects 
$N/S$, which is prescribed in homogeneous simulations, to output quantities on the right-hand side.
We plot the quantities on the right-hand side of (3.6a,b) as a function of a scaled version of the non-dimensional shear parameter and the gradient Richardson number in figure 3 for the SKIF and YK datasets. The dashed lines represent 
$y = 100x$ (black) and 
$y = x^{1/2}$ (blue), respectively, and the points that lie close to these dashed lines indicate statistically stationary turbulence. For the SKIF dataset, we see that only the simulations with 
$Ri_{g} \approx 0.1$ to 
$0.2$ lie close to the dashed lines, which corresponds to the range of stationary 
$Ri_{g}$ values observed in Shih et al. (Reference Shih, Koseff, Ferziger and Rehmann2000). Simulations with 
$Ri_{g}$ outside of this range, however, deviate from the dashed lines, corresponding to either temporally growing (
$Ri_{g} < 0.1$) or decaying conditions (
$Ri_{g} > 0.2$). In contrast, the YK simulations exhibit statistically stationary behaviour for 
$Ri_{g} \approx 10^{-3}$ to 
$1$ indicated by their proximity to the dashed lines. We take this as another verification that our numerical solver is accurately evaluating equations (3.1)–(3.3).
Before testing our revised scaling relationships using the SKIF and YK datasets, we would like to summarize as follows. The stably stratified, homogeneous shear flow of SKIF and the stably stratified, shear-forced model problem studied here exhibit meaningful differences as shown in figures 2 and 3. In particular, they evolve differently in time for a given value of 
$Ri_{g}$ due to the presence or absence of advection by the mean flow, which physically shears and elongates the turbulent structures in true shear flows. These effects have important implications for the transition to turbulence (Mashayek & Peltier Reference Mashayek and Peltier2011, Reference Mashayek and Peltier2012a,Reference Mashayek and Peltierb) as well as for the mixing properties of scalars in these flows once turbulence is established (e.g. Salehipour & Peltier Reference Salehipour and Peltier2015). Nonetheless, because the volume-averaged TKE and TPE dynamics of both flows are described by (3.4) and (3.5), the shear-forced model problem provides an additional way to test our revised scaling relationships described in § 2.2. In the next section, we will demonstrate that the power-law scaling relationships connecting 
$\varGamma$, 
$S_{\ast }$, and 
$Fr_k$ remain intact for the YK dataset despite these differences and that only the values of the proportionality constants are modified.
Figure 2. Values of (a) 
$b_{13}$, (b) 
$S_{*}$, (c) 
$Fr_{k}$ as a function of 
$Ri_{g}$ for the SKIF (squares) and YK (circles and stars) datasets with 
$Re_{b}$ shown in colour. Time-median values are plotted for the SKIF dataset, and time-averaged values are plotted for the YK dataset. Horizontal dashed lines in panels (a,b) correspond to typical ranges of 
$b_{13}$ and 
$S_{*}$ found from experiments and DNS of homogeneous shear flows that were reported in table 2 of Kasbaoui et al. (Reference Kasbaoui, Patel, Koch and Desjardins2017) (note that there is a factor of 
$2$ difference in what is plotted in panel (b) due to 
$q^{2} = 2k$ being typically used to define 
$S_{*}$).
Figure 3. Plot of right-hand side of (3.6a,b) vs a scaled version of the non-dimensional shear parameter and the gradient Richardson number for the SKIF and YK datasets. The scale of the 
$x$-axis is the same for both quantities. Here, 
$Ri_{g}$ is also shown in colour such that 
$Ri_{g} = 1/4$ is shown in light grey. Data that lie along the dashed lines indicate statistically stationary turbulence. The SKIF simulations classified in the paper as stationary (
$Ri_{g} \approx 0.1$ to 
$0.2$) lie close to the dashed lines, but the SKIF simulations that deviate from the dashed lines indicate temporal growth (
$Ri_{g} < 0.1$) or decay (
$Ri_{g} > 0.2$). Most of the YK simulations lie close to the dashed lines.
4. Results
4.1. Revised scaling validation using two homogeneous DNS datasets
We plot the irreversible mixing coefficient 
$\varGamma = \epsilon _p / \epsilon _k$ as a function of the turbulent Froude number 
$Fr_k$ in figure 4(a) for the SKIF and YK datasets. While the SKIF dataset contains time-varying simulations where 
$B \neq \epsilon _p$, we still opt to use the irreversible mixing coefficient given its positive semi-definite property compared with the reversible definition 
$B / \epsilon _k$, which can become negative for large values of 
$Ri_g$ (see figure 1 of Venayagamoorthy & Koseff Reference Venayagamoorthy and Koseff2016). The small squares (coloured by 
$Ri_{g}$) represent volume-averaged, time-varying values from the SKIF dataset, while the small stars (coloured by 
$Ri_{g}$) represent the volume-averaged, time-varying values from the YK dataset. For the SKIF dataset, the majority of the simulations are either growing or decaying, with only cases with 
$Ri_g \approx 0.1$ to 
$0.2$ exhibiting statistical stationarity. For the YK dataset, all simulations exhibit statistical stationarity (as demonstrated in figures 1 and 3), and therefore, the time-varying values are only selected from the statistically stationary portions of these simulations. The white squares and stars represent the time-median values from the SKIF dataset and time-mean values from the YK dataset, respectively. From figure 4(a), we see that the median and time-averaged values of the SKIF and YK datasets seem to exhibit a 
$\varGamma \sim Fr_k^{-2}$ behaviour (solid black line) beyond values of 
$Fr_k \approx 0.6$ and 
$0.7$. This point is further emphasized by the inset showing the results from simulations C1–C6 and R1 of the YK dataset, which shows 
$\varGamma Fr_{k}^{2} \approx \text {const.}$ with small deviations due to the effects of mean shear. For 
$Fr_{k} < 0.6$ and 
$Fr_{k} < 0.7$, the behaviour seemingly shifts (over a very narrow region) to 
$\varGamma \sim Fr_k^{-1}$ (dashed black line) before flattening out to values of 
$\varGamma \approx 0.35$ and 
$0.5$ (dashed-dotted black line) for the SKIF and YK datasets, respectively. We will discuss the YK simulation with 
$Ri_{g} = 1$ (blue stars) in a subsequent paragraph.
Figure 4. Values of (a) 
$\varGamma$ and (b) 
$\varGamma S_{\ast }$ as a function of 
$Fr_k$ for SKIF and YK datasets. Volume-averaged but time-varying quantities are shown in coloured squares (SKIF) and stars (YK) where the colour bar shows 
$Ri_{g}$ such that 
$Ri_{g} = 1/4$ is shown in light grey. White squares indicate the volume-averaged, time-median values from the SKIF dataset, while the white stars indicate volume- and time-averaged values from the YK dataset. In panel (a), the solid, dashed, and dashed-dotted lines mark the 
$\varGamma \sim Fr_k^{-2}$, 
$Fr_k^{-1}$ and 
$Fr_k^0$ relationships, respectively. In panel (b), the solid and dashed-dotted lines mark the 
$\varGamma S_{\ast } \sim Fr_k^{-2}$ and 
$Fr_k^{-0.5}$ relationships, respectively, and the red dashed line marks 
$\varGamma S_{*} \sim Fr_{k}^{-1}$, which seems to describe the YK dataset for 
$Fr_{k} < 0.1$ since 
$\varGamma \approx 0.4$ and 
$S_{*} = 1/Fr_{k}$ when 
$Ri_{g} = 1$. Furthermore, three insets with compensated 
$y$-axes are included for easier visual comparison with the GV and revised scaling relationships. Only simulations C1–C6 and R1 are shown in the sole inset in panel (a) and the top right inset in panel (b). The bottom left inset in panel (b) tests the scaling relationship for sheared, strongly stratified turbulence.
Next, we test our revised scaling by plotting 
$\varGamma S_{\ast }$ as a function of 
$Fr_k$ for the SKIF and YK datasets in figure 4(b). We note that the both datasets exhibit 
$\varGamma S_{\ast } \sim Fr_k^{-2}$ (solid black line) for values beyond 
$Fr_k \approx 0.6$ (SKIF) and 
$0.7$ (YK) in agreement with our revised scaling for weakly stratified sheared turbulence. Notably, we do not observe the moderately stratified sheared turbulence scaling of 
$\varGamma S_{\ast } \sim Fr_k^{-1}$, but both datasets curve over to exhibit 
$\varGamma S_{\ast } \sim Fr_k^{-0.5}$ behaviour (dashed-dotted black line), which is our empirical fit for the strongly stratified sheared regime. Compared with the GV scaling (figure 4a), both the median and time-averaged (white squares and stars) and the time-varying (coloured squares and stars) values exhibit improved collapse under our revised scaling (figure 4b). This is especially highlighted by the reduced scatter for 
$0.4 < Fr_k < 0.7$ for the SKIF dataset under our revised scaling (panel b) compared with what is observed under the GV scaling (panel a). However, we note that the YK simulation with 
$Ri_g = 1$ (blue stars) deviates from the empirical scaling of 
$\varGamma S_{\ast } \sim Fr_k^{-0.5}$ for strongly stratified sheared turbulence for 
$Fr_k < 0.1$ (see the bottom left inset in figure 4b). This simulation exhibits 
$\varGamma \approx 0.4$ for 
$Fr_k < 0.1$ (figure 4a), which is a smaller value than the initial plateau of 
$\varGamma \approx 0.5$ for 
$0.2 < Fr_k < 0.5$. A similar behaviour has been observed for the forced (unsheared), stably stratified turbulence simulations of Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) and Yi & Koseff (Reference Yi and Koseff2022) for very strong stable stratifications.
There are two possible interpretations for this behaviour of 
$\varGamma < \varGamma _{max}$ for decreasing 
$Fr_k$. First, we could interpret this as a fourth regime (distinct from the three considered by the GV scaling), similar to that observed for 
$Fr < 0.3$ in figure 4 from the simulations of Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) and 
$Fr_{k} < 0.1$ in figure 6(b) from the simulations Yi & Koseff (Reference Yi and Koseff2022). Second, by relaxing our constraint that 
$Ri_g < 1$ (
$\tau _S < \tau _B$) while keeping 
$S_{\ast } > 1$ (
$\tau _S < \tau _L$), we can choose 
$\tau _1 \tau _2 \sim \tau _S \tau _B = \tau _B^2$ (since 
$Ri_{g} = 1$ for this simulation), which results in 
$\varGamma \sim Fr_k^0 \approx \text {const.}$ when substituted into (2.1). This seems to agree with the behaviour shown in figure 4(a) where 
$\varGamma \approx 0.4$ for 
$Fr_k < 0.1$ (blue stars). Since 
$\varGamma \approx 0.4$ for 
$Fr_k < 0.1$ for the YK simulation with 
$Ri_g = 1$, we expect the data from this simulation to follow 
$S_{\ast } = 1/Fr_k$, which is shown in figure 4(b) using a red dashed line.
Finally, we plot 
$\varGamma$ as a function of 
$Re_{b}$ in figure 5(a) with 
$Ri_{g}$ in colour for the SKIF (squares) and YK (circles and stars) datasets. Panels (b,c) show the same data but with the 
$y$-axis variable multiplied by 
$Re_{b}^{1/2}$ and 
$Re_{b}$, respectively, for easier visual comparison with the expected scaling relationships. Both the SKIF and YK datasets exhibit 
$\varGamma \sim Re_{b}^{-1/2}$ (
$Re_{b} > 30$ for SKIF and 
$30 < Re_{b} < 500$ for YK) as suggested by Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005). The YK dataset, however, also exhibits 
$Re_{b}^{-1}$ scaling for 
$Re_{b} > 500$, which agrees with 
$\varGamma \sim Fr_{k}^{-2}$ (see figure 4a) following Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) that 
$Re_{b} = Re_{L} Fr_{k}^{2}$. Based on our observation that 
$S_{*} \approx 2$ for 
$Ri_{g} < 0.1$ (figure 2b), this behaviour is in agreement with our revised scaling relationship for sheared, weakly stratified turbulence that 
$\varGamma \sim Fr_{k}^{-2} S_{*}^{-1}$. However, 
$S_{*}$ still varies for 
$Ri_{g} < 0.1$, albeit weakly, and accounting for this variability does lead to an improved characterization of 
$\varGamma$. In particular, simulations C1–C6 and R1 of the YK dataset, corresponding to very weakly stratified conditions, are shown in the bottom left inset of figure 4(a) and top right inset of figure 4(b). The 
$y$-axis variable has been compensated by 
$Fr_{k}^{2}$ and 
$S_{*} Fr_{k}^{2}$, respectively, so that the time-averaged values of 
$\varGamma$ would lie along a flat line if they were well described by the GV or revised scaling relationships. Focusing first on the bottom left inset of figure 4(a), the time-averaged values of 
$\varGamma$ from simulations C1–C6 and R1 exhibit good agreement with the weakly stratified scaling relationship of GV, but we observe small deviations away from the flat line for simulations corresponding to the larger three 
$Ri_{g}$ values. Moving now to the top right inset of figure 4(b), the time-averaged values of 
$\varGamma$ from simulations C1–C6 and R1 exhibit excellent agreement with our revised weakly stratified scaling relationship, which is shown by the straight line going through all seven white stars. As shown by the large changes in 
$S_{*}$ for 
$Ri_{g} > 0.1$ in figure 2(b), the effects of 
$S_{*}$ grow increasingly important with increasing stratification. While the effects of 
$S_{*}$ seem less pronounced for weakly stratified conditions, we believe our revised scaling relationships provide an important extension of the GV scaling relationships by explicitly accounting for the effects of mean shear.
Figure 5. Value of 
$\varGamma$ as a function of 
$Re_{b}$ with (a) no compensation, (b) compensation by 
$Re_{b}^{1/2}$ and (c) compensation by 
$Re_{b}$ for the SKIF and YK datasets. The values of 
$Ri_{g}$ are shown in colour such that 
$Ri_{g} = 1/4$ is shown in light grey.
4.2. Applicability testing for more complex sheared, stably stratified turbulent flows
4.2.1. Observations
In this section, we explore the degree of applicability of our revised scaling for the mixing coefficient when some of our simplifying assumptions are relaxed. First, we apply our revised scaling relationships to the DNS dataset of Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022), hereafter IWAN, who considered a spatio-temporally evolving, open channel flow in the presence of radiative heating. This flow is vertically inhomogeneous, and it also has temporally evolving background stratification and shear profiles (i.e. 
$N^2 (z,t )$ and 
$S ( z,t )$). We choose to analyse the IWAN dataset in two ways: (i) using all data for 
$t > 1$ and 
$0.2 < z < 0.8$ as in Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022) but keeping only the data with 
$Re_b > 5$ to exclude the viscosity-affected stratified flow regime (Brethouwer et al. Reference Brethouwer, Billant, Lindborg and Chomaz2007); (ii) using all data for 
$t > 1$ but limiting the vertical range to 
$0.2 < z < 0.4$ to minimize the effect of vertical transport terms so that the data are well characterized by the simplified TKE balance of 
$d_{t} k \approx P_k - B - \epsilon _k$. This allows us to consider the part of the IWAN dataset that corresponds more closely to the homogeneous turbulence dynamics of the SKIF and YK datasets given that enhanced values of the mixing efficiency can be observed even in conditions with weak production but enhanced transport of TKE (e.g. Chamecki, Dias & Freire Reference Chamecki, Dias and Freire2018; Freire et al. Reference Freire, Chamecki, Bou-Zeid and Dias2019). We choose a conservative upper limit of 
$z = 0.4$ based on the statistically stationary profiles of the vertical transport terms of TKE for similar flow configurations as the IWAN dataset that were shown in figure 10(b) of Williamson et al. (Reference Williamson, Armfield, Kirkpatrick and Norris2015). While their figure shows that the transport term decreases in relative importance with larger stability parameters (
$\lambda _0$) for 
$0.4 < z < 0.8$, we still apply 
$z = 0.4$ as the upper limit because in § 5.3 of Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022) we are told that ‘all simulations [of the IWAN dataset] are still significantly distant from their final equilibrium states’ and that ‘the mean shear 
$S$ is still increasing to obtain shear stress equilibrium such that 
$Ri_g$ is still evolving toward its stationary state’. We note that our second analysis approach with subsampled data for 
$0.2 < z < 0.4$ already satisfies 
$Re_b > 5$. Finally, because the background stratification profile evolves in time, Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022) opted to use the reversible definition of the mixing coefficient 
$\varGamma _r = B / \epsilon _k$. Therefore, when applying the GV and our revised scaling relationships to the IWAN dataset, we consider how 
$\varGamma _r$ depends on 
$Fr_k$ and 
$S_{\ast }$.
We also apply our revised scaling relationships to field measurements of stably stratified atmospheric boundary-layer turbulence that were collected during the MATERHORN program (Fernando et al. Reference Fernando2015) and studied by Conry et al. (Reference Conry, Kit and Fernando2020) for times when the turbulence dynamics was expected to be well described by the simplified homogeneous TKE and TPE budgets in (3.4) and (3.5) (see Appendix A for more discussion about this assumption). The turbulence is characterized by Taylor microscale Reynolds numbers of 
$Re_\lambda = \lambda \sqrt {u^2} / \nu \sim {O} ({10}^2\unicode{x2013}{10}^3)$ and buoyancy Reynolds numbers of 
$Re_b=\epsilon _k/(\nu N^2 ) \sim {O}({10}^3\unicode{x2013}{10}^7)$, where 
$\lambda =(15\nu u^2/\epsilon _k)^{1/2}$ is the Taylor microscale, and 
$u^2$ is the squared streamwise velocity fluctuations. In applying the GV and our revised scaling relationships, we need to account for the fact that the measured variables differ in two ways from those used for the scaling validation with the homogeneous DNS datasets. First, only the streamwise component of the TKE is provided, so we estimate 
$k \sim u^2$ and define an alternative non-dimensional shear parameter and turbulent Froude number as 
$S_u = S u^2 / \epsilon _k$ and 
$Fr_u = \epsilon _k / ( N u^2 )$. Second, because only the buoyancy flux is provided, we once again consider the reversible mixing coefficient 
$\varGamma _r = B / \epsilon _k$ and its relationship with 
$Fr_u$ and 
$S_u$.
To characterize these two additional datasets in relation to the previously considered homogeneous DNS datasets, we consider the joint probability density function (p.d.f.) of 
$Fr_k$ and 
$S_{\ast }$ from the IWAN dataset in figure 6 with the time-median and time-averaged values from the SKIF and YK datasets marked using squares and stars, respectively, along with the measurements from Conry et al. (Reference Conry, Kit and Fernando2020) marked using red dots. In figure 6(a), all of the IWAN dataset for 
$t>1$ and 
$0.2< z<0.8$ with 
$Re_b>5$ is used to calculate the joint p.d.f., while in figure 6(b), a limited portion of the IWAN dataset for 
$t>1$ and 
$0.2< z<0.4$ is used to calculate the joint p.d.f. The dashed and solid diagonal lines indicate 
$Ri_g = 1/4$ and 
$1$, respectively, for 
$S_{\ast } \geqslant 1$, and the solid horizontal line indicates 
$S_{\ast } = 1$ for 
$Ri_g \leqslant 1$. The three DNS datasets all exhibit 
$S_{\ast } > 1$, which is one of the limits that were imposed in § 2.2 to arrive at our revised scaling relationships for 
$\varGamma$. The YK dataset broadly exhibits two sets of relationship between 
$S_{\ast }$ and 
$Fr_k$: (i) weak relationship between 
$S_{\ast }$ and 
$Fr_k$ for 
$Fr_k > 0.3$, and (ii) strong relationship between 
$S_{\ast }$ and 
$Fr_k$ for 
$Fr_k < 0.3$. The SKIF dataset exhibits a weak relationship between 
$S_{\ast }$ and 
$Fr_k$ for its range of 
$Fr_k$ (
$0.2$ to 
$1$), and 
$S_{*}$ remains fairly constant as shown in Shih et al. (Reference Shih, Koseff, Ferziger and Rehmann2000). For 
$Fr_k > 0.7$, the IWAN dataset exhibits strongly correlated values of 
$S_\ast$ and 
$Fr_k$ but weak rate of change of 
$S_{\ast }$ with respect to 
$Fr_k$, corresponding to the weakly stratified regime. For 
$Fr_k < 0.7$, the IWAN dataset exhibits a strong rate of change of 
$S_\ast$ with respect to 
$Fr_k$, but the spread in the data suggests a weak correlation between the two quantities, especially for data characterized by 
$Ri_g > 1/4$ (region between the dashed and solid diagonal lines in figure 6a). We note that this weaker correlation for 
$Ri_g > 1/4$ is associated with the dataset from 
$0.4 < z < 0.8$ where the mean shear varies temporally and vertical transport terms are expected to be playing an important role. We return to this point regarding additional physical effects in the following paragraphs when exploring the relationships among 
$\varGamma _r$, 
$Fr_k$ and 
$S_{\ast }$. Finally, we note that the field measurements studied by Conry et al. (Reference Conry, Kit and Fernando2020) exhibit the most variability of 
$Fr_u$ and 
$S_u$ with many data points with 
$Fr_u > 1$ exhibiting 
$S_u < 1$, which is technically outside the bounds of applicability of our revised scaling, and most of the measurements lie close to the 
$Ri_g = 1/4$ line.
Figure 6. Joint p.d.f. of 
$Fr_k$ and 
$S_{\ast }$ of the IWAN dataset (light to dark colour bar) with time-median values of SKIF dataset (squares), time-mean values of the YK dataset (stars) and Conry et al. (Reference Conry, Kit and Fernando2020) dataset (red dots). The joint p.d.f. in panel (a) is calculated using the IWAN dataset for 
$t>1$, 
$0.2 < z < 0.8$, 
$Re_b > 5$, while the joint p.d.f. in panel (b) is calculated using the IWAN dataset for 
$t>1$, 
$0.2 < z < 0.4$. Dark colours denote larger joint p.d.f. values, and the discrete sums over the bins add to unity. Red dots denote the 
$Fr_u$ and 
$S_u$ values from Conry et al. (Reference Conry, Kit and Fernando2020). The dashed and solid diagonal lines indicate 
$Ri_g = 1/4$ and 
$1$ for 
$S_{\ast } \geqslant 1$. The solid horizontal line indicates 
$S_{\ast } = 1$ for 
$Ri_g \leqslant 1$.
In figure 7, we consider the joint p.d.f.s of 
$Fr_k$ and 
$\varGamma _r$ in panels (a,c) and the joint p.d.f.s of 
$Fr_k$ and 
$\varGamma _r S_{\ast }$ in panels (b,d). Panels (a,b) correspond to the first analysis approach where the IWAN dataset has only been subsampled to satisfy 
$Re_b > 5$, and panels (c,d) correspond to the second analysis approach where the IWAN dataset has been subsampled for 
$0.2 < z < 0.4$ to reduce the effects of time-varying mean shear and vertical transport terms. The GV scaling is revisited in figures 7(a) and 7(c) using the IWAN dataset, and we observe 
$\varGamma _r \sim Fr_k^{-2}$ for 
$Fr_k > 0.7$, 
$\varGamma _r \sim Fr_k^{-1}$ for 
$0.3 < Fr_k < 0.7$ and 
$\varGamma _r \approx 0.3$ for 
$Fr_k < 0.3$, where this last regime is less visibly obvious due to the subsampling for points satisfying 
$Re_b > 5$ (see figure 6(b) of Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022) for a more visibly obvious demonstration of 
$\varGamma _{r} \approx 0.3$ for 
$Fr_{k} < 0.3$). Overall, in figures 7(a) and 7(c), the joint p.d.f.s of the IWAN dataset agree well with the time-median values of the SKIF dataset, and broadly, the three datasets exhibit the same relationships between 
$\varGamma _r$ and 
$Fr_k$. We note that Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022) used 
$Fr_k \approx 1$ rather than 
$Fr_k \approx 0.7$ as their boundary value between the weakly stratified and moderately stratified regimes, and we observe that the subsampled IWAN dataset in figures 7(c) and 7(d) excludes much of 
$Fr_k < 0.3$. Next, we consider our revised scaling in figures 7(b) and 7(d) using the IWAN dataset. First, when considering the entire IWAN dataset for 
$Re_{b} > 5$ (figure 7b), we observe 
$\varGamma _r S_{\ast } \sim Fr_k^{-2}$ for 
$Fr_k > 0.7$, but we observe an intermediate scaling of 
$\varGamma _r S_{\ast } \sim Fr_k^{-\alpha }$ with 
$1< \alpha < 2$ for 
$0.3 < Fr_k < 0.7$. For 
$Fr_k < 0.3$, the IWAN dataset exhibits scatter that lies between 
$\varGamma _r S_{\ast } \sim Fr_k^{-\beta }$ where 
$0.5 < \beta < 1$, where the smaller power-law slope of 
$-0.5$ agrees with the empirical relationship found for strongly stratified sheared turbulence using the SKIF and YK datasets (see figure 4b) and the larger power-law slope of 
$-1$ agrees with the moderately stratified sheared turbulence from § 2.2. When we subsample the IWAN dataset for only 
$0.2 < z < 0.4$, the remaining data points in figure 7(d) broadly exhibit 
$\varGamma _r S_{\ast } \sim Fr_k^{-2}$, indicating that the excluded, strongly stratified portions of the IWAN dataset with 
$Fr_k < 0.3$ exhibit more complicated physics due to unsteady and vertical transport terms that are absent for the SKIF and YK datasets. The SKIF and subsampled IWAN datasets also exhibit good agreement under our revised scaling because the turbulence dynamics for these two flows are very similar for these heights (i.e. well described by (3.4) and (3.5)).
Figure 7. Joint p.d.f.s of 
$Fr_k$ and (a) 
$\varGamma _r$ or (b) 
$\varGamma _r S_{\ast }$ of the IWAN dataset for 
$t>1$, 
$0.2 < z < 0.8$, and 
$Re_b > 5$, and joint p.d.f.s of 
$Fr_k$ and (c) 
$\varGamma _r$ or (d) 
$\varGamma _r S_{\ast }$ of the IWAN dataset for 
$t>1$, 
$0.2 < z < 0.4$. Dark colours denote larger joint p.d.f. values, and the discrete sums over the bins add to unity. White squares and stars indicate the time-median values of the SKIF dataset and time-mean values of the YK dataset, respectively, and the irreversible mixing coefficient values are used (
$\varGamma = \epsilon _p / \epsilon _k$). In panels (a,c), the solid, dashed and dashed-dotted lines mark the 
$\varGamma \sim Fr_k^{-2}$, 
$Fr_k^{-1}$ and 
$Fr_k^0$ relationships, respectively. In panels (b,d), the solid, dashed and dashed-dotted lines mark the 
$\varGamma S_{\ast } \sim Fr_k^{-2}$, 
$Fr_k^{-1}$ and 
$Fr_k^{-0.5}$ relationships, respectively.
In figure 8(a), we plot the reversible mixing coefficient 
$\varGamma _r$ as a function of 
$Fr_u$ using the measurements provided in Conry et al. (Reference Conry, Kit and Fernando2020). The data have been colour coded based on the magnitude of 
$S_u$ (blue for 
$S_u > 1$ and red for 
$S_u \leqslant 1$) to distinguish the points that strictly satisfy the requirements for the revised scaling of 
$S_{\ast } \sim S_u > 1$. As described in Conry et al. (Reference Conry, Kit and Fernando2020) (and seen in figure 8a), these field measurements exhibit 
$\varGamma _r \sim Fr_u^{-1}$ over most of the 
$Fr_u$ range (which agrees with the moderately stratified regime of the GV scaling) except for the lowest values of 
$Fr_u$ (which are possibly beginning to show 
$\varGamma _r \approx \text {const.}$) and the largest values of 
$Fr_u$, where a 
$Fr_u^{-2}$ fit seems more appropriate. However, when we plot 
$\varGamma _r S_u$ as a function of 
$Fr_u$ in figure 8(b), we note that the dataset switches to exhibiting 
$\varGamma _r S_u \sim Fr_u^{-2}$, which is expected for weakly stratified sheared turbulence from our revised scaling. Qualitatively, this shift agrees with the majority of the measurements having been collected during conditions with 
$Ri_g < 1/4$, and this also broadly agrees with the behaviour of the three DNS datasets for 
$Ri_g < 1/4$.
Figure 8. Values of 
$\varGamma _r$ and 
$\varGamma _r S_u$ as a function of 
$Fr_u$ using the field measurements studied by Conry et al. (Reference Conry, Kit and Fernando2020). In panel (a), the solid and dashed lines mark the 
$\varGamma \sim Fr_k^{-2}$ and 
$Fr_k^{-1}$ relationships, respectively. In panel (b), the solid and dashed lines mark the 
$\varGamma S_{\ast } \sim Fr_k^{-2}$ and 
$Fr_k^{-1}$ relationships, respectively.
4.2.2. Implications
We would like to highlight two somewhat unresolved issues based on our observations from figure 7. First, the power-law relationships between 
$\varGamma S_{\ast }$ and 
$Fr_k$ for intermediate values of 
$Fr_k$ (e.g. 
$0.3 < Fr_k < 0.7$) are different for the homogeneous, sheared, stably stratified turbulence with constant values of 
$N^2$ and 
$S$ (SKIF and YK datasets) compared with the sheared, stably stratified turbulence with time-varying values of 
$N^2$ and 
$S$ (IWAN dataset). For the IWAN dataset, 
$\partial _t S \neq 0$ and the temporal evolution of the flow seems to be having a significant effect on the local turbulence dynamics. We, therefore, expect that introducing a fourth time scale associated with 
$\partial _t S$ when considering (2.1) will address a part of this discrepancy. However, the inhomogeneous effects that are present via the vertical transport terms cannot be fully accounted for by this approach. In an attempt to illustrate this point, we isolated the data from the lower heights 
$0.2 < z < 0.4$ of the IWAN dataset, where the mean shear varies negligibly in time and the vertical transport terms are weak. When we do this, the SKIF and subsampled IWAN datasets agree well, and both datasets exhibit the revised scaling of 
$\varGamma _r S_{\ast } \sim Fr_k^{-2}$ for 
$Fr_k > 0.7$. Second, we note that the limit of very strong stably stratified turbulence is inaccessible from the IWAN dataset given that most of the dataset for 
$Re_b > 5$ is characterized by 
$Fr_k > 0.1$. Therefore, it remains to be seen whether the decrease of 
$\varGamma$ from its maximum value and the subsequent plateau for 
$Fr_k < 0.1$ noted from the YK simulation with 
$Ri_g = 1$ (see figure 4a) would also hold true for other vertically sheared stably stratified turbulent flows.
To resolve the first issue, longer time integration would be necessary until the vertical profiles of 
$S_{\ast }$ became well developed, at which point the dynamically relevant time scales in the IWAN problem would reduce to the same, three, time scales as in the homogeneous, sheared, stably stratified problems explored through the SKIF and YK datasets. Any remaining discrepancy between this statistically steady version of the IWAN dataset and the SKIF and YK datasets could then be unambiguously attributed to vertical transport terms. To resolve the second issue, additional simulations with negligible temporal variations of 
$N^2$ and 
$S$ and with 
$Ri_g > 1/4$ would need to be explored, which might be challenging given that statistically stationary, sheared, stably stratified turbulence in the presence of walls have typically shown a maximum 
$Ri_g \approx 0.2$ at heights satisfying energy equilibrium, 
$P_k \approx B +\epsilon _k$ (e.g. fully developed, radiatively heated, open channel flow studied by Williamson et al. (Reference Williamson, Armfield, Kirkpatrick and Norris2015); fully developed, stably stratified, plane Couette flow studied by Zhou, Taylor & Caulfield Reference Zhou, Taylor and Caulfield2017).
4.3. Connections to 
$Ri_{g}$ parameterizations of $\varGamma$
Because values of mean shear and stratification are easily measurable and accessible in large-scale modelling contexts, subgrid-scale mixing parameterizations based on 
$Ri_g$ are regularly used (e.g. Large, McWilliams & Doney Reference Large, McWilliams and Doney1994; Jackson, Hallberg & Legg Reference Jackson, Hallberg and Legg2008; Roekel et al. Reference Roekel, Adcroft, Danabasoglu, Griffies, Kauffman, Large, Levy, Reichl, Ringler and Schmidt2018). Therefore, we now examine the connections between our revised scaling and existing ones based on 
$Ri_g$. For example, a synthesis of field measurements, laboratory experiments and numerical simulations by Katul et al. (Reference Katul, Porporato, Shah and Bou-Zeid2014) shows the mixing efficiency 
$Ri_f = \varGamma / (1 + \varGamma )$ scaling as 
$Ri_f \sim Ri_g$ for 
$Ri_g < 1/4$ and 
$Ri_f \approx \text {const.}$ for 
$Ri_g > 1/4$. Using Monin–Obukhov similarity theory, Zhou et al. (Reference Zhou, Taylor and Caulfield2017) showed 
$Ri_f \sim Ri_g$ and 
$Fr \sim Ri_g^{-1/2}$, which combined to 
$Ri_f \sim Fr^{-2}$. They confirmed this scaling using DNS of fully developed, stably stratified, plane Couette flow for varying Reynolds, Richardson and molecular Prandtl numbers. This scaling has also been observed by Kirkpatrick et al. (Reference Kirkpatrick, Williamson, Armfield and Zecevic2019) and Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022) using DNS of open-channel flow with temporally evolving thermal stratification.
Using the relationship that 
$Fr_k = Ri_g^{-1/2} S_{\ast }^{-1}$, we can rewrite our revised scaling relationships in table 2 only in terms of 
$Ri_g$ and 
$S_{\ast }$. For the weakly stratified sheared regime, this leads to 
$\varGamma \sim Ri_g S_{\ast }$, and for the strongly stratified sheared regime, this leads to 
$\varGamma \sim Ri_g^{1/4} S_{\ast }^{-1/2}$. In figures 2 and 6, we see that 
$S_\ast$ weakly varies with 
$Fr_{k}$ for weak stratification strengths (
$Fr_k>0.7$) for all three datasets, which explains why all three DNS datasets exhibited 
$\varGamma \sim Fr_k^{-2}$ and 
$\varGamma S_{\ast } \sim Fr_k^{-2}$ for this range of turbulent Froude numbers, which simplifies to 
$\varGamma \sim Ri_f \sim Ri_g$. In figures 9(a) and 9(b), we plot the joint p.d.f. of the gradient Richardson number (
$Ri_g$) and the reversible mixing efficiency (
$Ri_{f,r} = B/ (\epsilon _k + B)$) for the full but 
$Re_{b} > 5$ and subsampled IWAN dataset, respectively. We also plot the median and time-averaged irreversible mixing efficiency (
$Ri_f = \epsilon _p / ( \epsilon _k + \epsilon _p )$) for the SKIF and YK datasets, respectively, as a function of the gradient Richardson number. In figure 9(a), all three datasets exhibit 
$Ri_f \sim Ri_g$ up to 
$Ri_g \approx 0.2$ before flattening out. While the time-varying values of 
$Ri_f$ from the SKIF and YK datasets are not shown, they would lead to vertical lines at each of the 
$Ri_g$ values of these simulations (see figure 4 of Venayagamoorthy & Koseff Reference Venayagamoorthy and Koseff2016), which remains constant for the entire simulation duration. We further illustrate this shortcoming by plotting 
$Ri_{f,r}$ as a function of 
$Ri_g$ in figure 9(c) using the field measurements studied by Conry et al. (Reference Conry, Kit and Fernando2020). Most of the field measurements do not exhibit the 
$Ri_f \sim Ri_g$ behaviour for 
$Ri_g < 0.2$, which strongly suggests that the measurement conditions are described by more complex physics than what is represented by the simplified energetic balance described in (3.4) and (3.5) (see Appendix A for further discussion). While 
$Ri_f \sim Ri_g$ has been shown to be a good approximation for 
$Ri_g < 0.2$ by Venayagamoorthy & Koseff (Reference Venayagamoorthy and Koseff2016) as well as Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022), we note that this relationship begins to break down for moderate and strong stratification strengths (
$Fr_k<0.7, Ri_g>0.2$), where 
$S_{\ast }$ exhibits stronger variation with 
$Fr_k$ and 
$Ri_f$ (or 
$\varGamma$) also exhibits greater variation for a given value of 
$Ri_g$ (see figure 4 of Venayagamoorthy & Koseff Reference Venayagamoorthy and Koseff2016).
Figure 9. Joint p.d.f. of reversible mixing efficiency (
$Ri_{f,r}$) and gradient Richardson number (
$Ri_g$) of the IWAN dataset for (a) for 
$t>1$, 
$0.2 < z < 0.8$, and 
$Re_b>5$ and (b) for 
$t>1$, 
$0.2 < z < 0.4$. Dark colours denote greater joint p.d.f. values, and the discrete sums over the bins add to unity. White squares and stars indicate the time-median values of the SKIF dataset and time-mean values of the YK dataset, respectively, and the irreversible mixing efficiency values are used, 
$Ri_f = \epsilon _p / ( \epsilon _k + \epsilon _p )$. 
$Ri_{f,r}$ as a function of 
$Ri_g$ from Conry et al. (Reference Conry, Kit and Fernando2020) is plotted in panel (c), where a one-to-one line is plotted for reference to indicate 
$Ri_f \sim Ri_g$.
4.4. Finite Reynolds number effects on mixing efficiency
Up to this point, both the GV and our revised scaling relationships have been presented in terms of 
$Fr_{k}$ and 
$S_{*}$. These two quantities primarily describe the effects of large, anisotropic scales of sheared, stratified turbulence, which is in contrast to the various Reynolds numbers that can be introduced for these flows (e.g. large-eddy, buoyancy and shear Reynolds numbers; 
$Re_{L}$, 
$Re_{b}$ and 
$Re_{S}$, respectively), which incorporate the effects of isotropic scales (see § 2.2 of Zhang et al. (Reference Zhang, Dhariwal, Portwood, de Bruyn Kops and Bragg2022) for a further overview and discussion about the energetics associated with the various ranges of scales in sheared, stably stratified flows). The primary variations of 
$\varGamma$ seem to be well captured by 
$Fr_{k}$ and 
$S_{*}$ based on our validation using the SKIF and YK datasets (figure 4) as well as by the IWAN dataset (figure 7) and the data studied by Conry et al. (Reference Conry, Kit and Fernando2020) (figure 8). Nevertheless, we expect 
$\varGamma$ to exhibit some sensitivity to the Reynolds number.
For forced (unsheared), stably stratified turbulence, Maffioli et al. (Reference Maffioli, Brethouwer and Lindborg2016) showed that 
$\varGamma$ decreases with increasing Taylor microscale Reynolds number (
$Re_{\lambda } \sim Re_{L}^{1/2}$) for weakly stratified conditions (
$Fr_{k} \approx 3$). This sensitivity, however, was weak compared with the large variations of 
$\varGamma$ that were observed by varying the turbulent Froude number at a fixed Reynolds number. For sheared, stably stratified turbulence under moderately stratified conditions (
$0.42 \lesssim Fr_{k} \lesssim 0.52$), Portwood et al. (Reference Portwood, de Bruyn Kops and Caulfield2019) also showed that 
$\varGamma$ decreases with 
$Re_{b}$, albeit very weakly. As 
$Re_{b}$ is increased, the dissipation scales become increasingly isotropic, but this effect seems weakly tied to the actual value of 
$\varGamma$ (see figures 1 and 2 of Portwood et al. Reference Portwood, de Bruyn Kops and Caulfield2019).
To explain this weak relationship between 
$\varGamma$ and the Reynolds number, which we take to be an estimate of the range of isotropic scales, we consider an alternative expression for the irreversible mixing efficiency (
$Ri_{f} = \epsilon _{p} / ( \epsilon _{k} + \epsilon _{p} )$) from Bou-Zeid et al. (Reference Bou-Zeid, Gao, Ansorge and Katul2018)
\begin{equation} Ri_{f} = \frac{1}{1-c_{3}} \left(\frac{R_{w}}{P_{k}} - c_{3} \right), \end{equation}
where 
$c_{3} = \epsilon _{w}/\epsilon _{k}$ is the fraction of the TKE dissipation rate that is accounted for by the dissipation rate of the vertical component of TKE (
$k_{w} = \overline {ww}/2$), 
$R_{w}$ is the pressure-strain correlation term in the 
$k_{w}$ budget, and 
$P_{k} = -\overline {uw} S$ is the rate of production of TKE. For large Reynolds numbers, 
$c_{3} \to 1/3$ as expected by the dissipation scales recovering local isotropy (e.g. Itsweire et al. Reference Itsweire, Koseff, Briggs and Ferziger1993; Portwood et al. Reference Portwood, de Bruyn Kops and Caulfield2019), and (4.1) can be simplified to
\begin{equation} \lim_{Re \gg 1} Ri_{f} = \frac{3}{2} \left(\frac{R_{w}}{P_{k}} - \frac{1}{3} \right). \end{equation} Equation (4.2) connects the irreversible mixing efficiency of homogeneous, sheared, stably stratified turbulence to the normalized pressure-strain correlation (
$R_{w}/P_{k}$), which is a large-scale quantity that is expected to primarily depend on 
$Fr_{k}$ and 
$S_{*}$ rather than on the Reynolds number.
To explore this further, we plot 
$R_{w}/P_{k}$ and 
$c_{3}$ as a function of 
$Fr_{k}$ with 
$Re_{S}$ shown in colour in figure 10(a,b). Here we have chosen 
$Re_{S}$ to represent the range of isotropic scales because for 
$Ri_{g} < 1$, the Corrsin scale (
$l_{C}$) is smaller than the Ozmidov scale (
$l_{O}$), making it a more appropriate estimate of the largest isotropic eddies for sheared, stably stratified flows when 
$Ri_{g} < 1$. In panel (a), the horizontal dashed line indicates the maximum value of 
$c_{3} \approx 0.31$. Given that 
$R_{w}/P_{k}$ is close to this value for 
$Fr_{k} \gg 1$, this matches our intuition that 
$Ri_{f} \to 0$ for 
$Fr_{k} \gg 1$ where there is no background scalar gradient to mix. As 
$Fr_{k}$ is decreased, 
$R_{w}/P_{k}$ increases until reaching a maximum at 
$Fr_{k} \approx 0.2$ for the C series simulations (circles) and reaching a plateau for 
$0.2 < Fr_{k} < 0.6$ for the R series simulations (stars). For 
$Fr_{k} < 0.2$, however, 
$R_{w}/P_{k}$ decreases with increasing stratification. In panel (b), the horizontal dashed line marks 
$1/3$, which is the value of 
$c_{3}$ that is expected for isotropic dissipation scales. The value of 
$c_{3}$ generally decreases with increasing stratification (this is because 
$Re_{S}$ decreases as stratification is increased due to the fixed resolution of our simulations), but for 
$0.2 < Fr_{k} < 1$, we see that 
$c_{3}$ grows with increasing 
$Re_{S}$, as seen by the change from purple to blue coloured symbols with increasing values of 
$c_{3}$. In panel (c), 
$( R_{w}/P_{k} - c_{3} )$ is plotted as a function of 
$Fr_{k}$ with 
$Re_{S}$ shown in colour. Focusing on 
$0.2 < Fr_{k} < 0.7$, where we observe large differences of 
$R_{w}/P_{k}$ and 
$c_{3}$ between the C and R series simulations due to changes in 
$Re_{S}$, we find that the difference, 
$( R_{w}/P_{k} ) - c_{3}$, does not seem as sensitive to 
$Re_{S}$ because the simultaneous changes to 
$R_{w}/P_{k}$ and 
$c_{3}$ seem to cancel out. Finally, in figure 10(d), we plot the two sides of (4.1) with 
$Fr_{k}$ shown in colour to check whether the YK dataset obeys this relationship, which we confirm based on the observation that the data lie along the one-to-one line.
Figure 10. Value of (a) 
$R_{w}/P_{k}$, (b) 
$c_{3}$, (c) 
$( R_{w}/P_{k} ) - c_{3}$ as a function of 
$Fr_{k}$ with 
$Re_{S}$ shown in colour. The horizontal dashed line in panel (a) indicates the maximum value of 
$c_{3} \approx 0.31$, and the horizontal dashed line in panel (b) marks 
$c_{3} = 1/3$, which is expected under conditions of local isotropy of dissipative scales. (d) Value of 
$Ri_{f}$ as a function of the right-hand side expression of (4.1) with 
$Fr_{k}$ in colour. The values from the YK dataset lie along the one-to-one line.
Lastly, (4.1) allows us to explore why the YK dataset exhibits larger values of 
$\varGamma$ (or 
$Ri_{f}$) relative to the SKIF dataset as observed in figures 4 and 9. For a given rate of TKE production and Reynolds number, the sheared flow that is associated with larger values of 
$R_{w}$ will be more efficient at irreversibly mixing out the background scalar gradient. For homogeneous sheared turbulence, the vertical component of TKE (
$k_{w}$) is the smallest (e.g. Kasbaoui et al. Reference Kasbaoui, Patel, Koch and Desjardins2017), which is further decreased by the effects of stable stratification as 
$Fr_{k}$ is decreased. For the shear-forced model problem, however, 
$k_{w}$ is actually the second largest component across all 
$Fr_{k}$ values (not shown), which suggests that this model problem involves larger values of 
$R_{w}/P_{k}$ compared with homogeneous sheared turbulence. Also, the volume-averaged vertical buoyancy flux budget has a source term that is linearly proportional to 
$k_{w}$ (e.g. Riley, Metcalfe & Weissman Reference Riley, Metcalfe and Weissman1981; Yi & Koseff Reference Yi and Koseff2022). Connecting these two thoughts, our hypothesis is that for a given rate of TKE production and stratification, the shear-forced model problem is associated with larger values of 
$R_{w}/P_{k}$ compared with homogeneous shear turbulence, leading to enhanced values of 
$k_{w}/k$, which can then generate larger vertical buoyancy fluxes. Under a steady-state balance, this implies a larger 
$\epsilon _{p}$ for a given 
$P_{k}$, and therefore a larger value of 
$Ri_{f}$. In closing this section, we stress that while 
$R_{w}/P_{k}$ in (4.1) seems to depend more sensitively on 
$Fr_{k}$, it does exhibit some relationship with 
$Re_{S}$. This observation should be looked at in more detail in the future.
5. Conclusions
We revisited the mixing coefficient scaling of Garanaik & Venayagamoorthy (Reference Garanaik and Venayagamoorthy2019) and modified them to include the effects of mean shear for vertically sheared, stably stratified turbulent flows. Through scaling analysis, we found 
$\varGamma \sim Fr_k^{-2} S_{\ast }^{-1}$ for the weakly stratified sheared regime and 
$\varGamma \sim Fr_k^{-1} S_{\ast }^{-1}$ for the moderately stratified sheared regime. While the scaling analysis was inconclusive for the strongly stratified sheared regime, we empirically observed 
$\varGamma \sim Fr_k^{-0.5} S_\ast ^{-1}$ using two distinct DNS datasets of homogeneous, stably stratified, sheared turbulence as well as the absence of the moderately stratified sheared regime. We then explored the degree of applicability of our revised scaling by considering two datasets of more complex, sheared, stably stratified turbulence. The first dataset was from the spatio-temporally varying, radiatively heated, open channel simulations of Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022), and the second dataset was from field measurements from the MATERHORN campaign that were provided in Conry et al. (Reference Conry, Kit and Fernando2020). The dataset of Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022) also exhibited 
$\varGamma _r S_{\ast } \sim Fr_k^{-2}$ for 
$Fr_k > 0.7$, but it neither exhibited the moderately stratified sheared scaling of 
$\varGamma S_{\ast } \sim Fr_k^{-1}$ nor the empirical strongly stratified sheared scaling of 
$\varGamma _r S_{\ast } \sim Fr_k^{-0.5}$ for 
$Fr_k < 0.7$, which we hypothesized are due to the effects of the vertical transport terms and time-varying mean shear that were unaccounted for when arriving at our revised scaling relationships. We attempted to explore this hypothesis by minimizing these two additional physical effects by only considering data from the zone where vertical transport was minimal in their simulations (
$0.2 < z < 0.4$), which resulted in mostly retaining the data exhibiting 
$\varGamma _r S_{\ast } \sim Fr_k^{-2}$ behaviour (for 
$Fr_k > 0.7$), which is in good agreement with the SKIF dataset. When we applied our revised scaling to the field measurements analysed by Conry et al. (Reference Conry, Kit and Fernando2020), the measurements followed the weakly stratified sheared scaling of 
$\varGamma _r S_u \sim Fr_u^{-2}$, which was expected given that most measurement conditions were characterized by 
$Ri_g < 1/4$. Finally, we explored the connection between our revised scaling and existing 
$Ri_g$ descriptions, and showed that 
$Ri_f \sim Ri_g$ for 
$0 < Ri_g < 0.2$ and 
$Ri_f \approx \text {const.}$ for 
$Ri_g > 0.2$. However, we noted that 
$Ri_g$ parameterizations remain inadequate for describing temporally varying datasets unlike our revised scaling relationships which include some information about temporal variations through 
$Fr_k$ and 
$S_\ast$. Lastly, we noted that values of 
$\varGamma$ from a simulation with 
$Ri_g = 1$ deviated from the empirical scaling for strongly stratified, sheared turbulence of 
$\varGamma S_{\ast } \sim Fr_k^{-0.5}$ and instead exhibited 
$\varGamma \approx \text {const.} < \varGamma _{max}$ for 
$Fr_k < 0.1$, for which we proposed two possible explanations.
In closing, we emphasize that our revised scaling relationships should also hold for other types of stably stratified turbulence with vertically sheared horizontal mean flows satisfying the simplified TKE balance of 
$d_{t} k \approx P_k - B - \epsilon _k$, but we have neglected the effects of Prandtl number (e.g. Salehipour, Peltier & Mashayek Reference Salehipour, Peltier and Mashayek2015; Schaad & Venayagamoorthy Reference Schaad and Venayagamoorthy2017; Legaspi & Waite Reference Legaspi and Waite2020) and the Reynolds number (briefly explored in § 4.4), which should be incorporated into (2.1) for a more complete description of irreversible mixing in sheared, stably stratified turbulent flows. Nevertheless, since our revised scaling relationships successfully describe the temporally evolving mixing statistics from Shih et al. (Reference Shih, Koseff, Ivey and Ferziger2005), we hypothesize that they might also apply to irreversible mixing occurring in stably stratified shear layers (Mashayek & Peltier Reference Mashayek and Peltier2011; Salehipour & Peltier Reference Salehipour and Peltier2015), especially when the mean shear and stratification evolve slowly relative to the turbulence statistics. Furthermore, relying on the connections between our revised scaling and 
$Re_{b}$-based descriptions that we explored in § 4, there is further hope for the applicability of these relations to stably stratified mixing layers whose mixing properties have been previously studied in terms of 
$Re_{b}$ (e.g. Salehipour & Peltier Reference Salehipour and Peltier2015; Mashayek et al. Reference Mashayek, Salehipour, Bouffard, Caulfield, Ferrari, Nikurashin, Peltier and Smyth2017; VanDine et al. Reference VanDine, Pham and Sarkar2021). However, given the challenges associated with accurate measurements of turbulence quantities such as 
$k$ and 
$\epsilon _{k}$ that are needed to estimate 
$Fr_{k}$ and 
$S_{*}$, it would be beneficial to develop a corresponding length-scale-based characterization of the mixing coefficient as done by Garanaik & Venayagamoorthy (Reference Garanaik and Venayagamoorthy2019) for forced (unsheared), stably stratified turbulence. To do this, we could leverage the large body of work on sheared, stably stratified flows that includes studies of the temporal evolution of various length scales (e.g. Itsweire et al. Reference Itsweire, Koseff, Briggs and Ferziger1993; Smyth & Moum Reference Smyth and Moum2000; Smyth, Moum & Caldwell Reference Smyth, Moum and Caldwell2001; Lewin & Caulfield Reference Lewin and Caulfield2021) as well as of the relationships between length-scale ratios and the degree of irreversible mixing of these flows (e.g. Ivey & Imberger Reference Ivey and Imberger1991; Mater & Venayagamoorthy Reference Mater and Venayagamoorthy2014b; Ivey, Bluteau & Jones Reference Ivey, Bluteau and Jones2018; Ijichi & Hibiya Reference Ijichi and Hibiya2018; Mashayek et al. Reference Mashayek, Caulfield and Alford2021, Reference Mashayek, Baker, Cael and Caulfield2022). Lastly, when considering stably stratified turbulence with different shear configurations such as spanwise shear (e.g. Billant & Chomaz Reference Billant and Chomaz2000a,Reference Billant and Chomazb; Basak & Sarkar Reference Basak and Sarkar2006; Deloncle, Chomaz & Billant Reference Deloncle, Chomaz and Billant2007; Waite & Smolarkiewicz Reference Waite and Smolarkiewicz2008; Lucas, Caulfield & Kerswell Reference Lucas, Caulfield and Kerswell2017; Cope, Garaud & Caulfield Reference Cope, Garaud and Caulfield2020) or flows with spatio-temporal variations (e.g. Williamson et al. Reference Williamson, Armfield, Kirkpatrick and Norris2015; Kirkpatrick et al. Reference Kirkpatrick, Williamson, Armfield and Zecevic2019, Reference Kirkpatrick, Williamson, Armfield and Zecevic2020; Onuki et al. Reference Onuki, Joubaud and Dauxois2021; Issaev et al. Reference Issaev, Williamson, Armfield and Norris2022; Lewin & Caulfield Reference Lewin and Caulfield2022), we expect the need for an expanded set of scaling relationships due to the differences in the turbulence generation mechanism or large-scale forcing (Howland et al. Reference Howland, Taylor and Caulfield2020) and the energy exchange pathways among the different components of TKE and TPE (Yi & Koseff Reference Yi and Koseff2022).
Acknowledgements
Y.R.Y. gratefully acknowledges support from the Charles H. Leavell Fellowship of the Department of Civil and Environmental Engineering at Stanford University. Some of the computing for this project was performed on the Sherlock cluster. We would like to thank Stanford University and the Stanford Research Computing Center for providing computational resources and support that contributed to these research results. The authors also greatly thank V. Issaev for sharing the DNS dataset that was analysed in Issaev et al. (Reference Issaev, Williamson, Armfield and Norris2022).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Steps taken to analyse the Conry et al. (Reference Conry, Kit and Fernando2020) dataset
Here, we seek to estimate the degree of statistical stationarity of the measurements that were analysed by Conry et al. (Reference Conry, Kit and Fernando2020). For a vertically sheared, stably stratified turbulent flow under statistically stationary and homogeneous conditions, TKE and TPE budgets are described by the balance of right-hand side terms in (3.4) and (3.5). Under these conditions, we can consider three different estimates of the mixing efficiency (
$Ri_f$) and the mixing coefficient (
$\varGamma = Ri_f / ( 1 - Ri_f )$)
\begin{gather} Ri_{f,1}=\frac{B}{P_k}, \quad \varGamma_1=\frac{B}{P_k-B}, \end{gather}
\begin{gather}Ri_{f,r}=\frac{B}{B+\epsilon_k}, \quad \varGamma_r=\frac{B}{\epsilon_k}, \end{gather}
\begin{gather}Ri_f=\frac{\epsilon_p}{\epsilon_p+\epsilon_k}, \quad \varGamma=\frac{\epsilon_p}{\epsilon_k}, \end{gather}
where the three definitions correspond to 
$R_f$, 
$R_f^{II}$, 
$R_f^{\ast }$ from Venayagamoorthy & Koseff (Reference Venayagamoorthy and Koseff2016). The second set of definitions (A2) can be reached from (A1) by substituting in for 
$P_k$ using (3.4). The third set of definitions (A3) can be reached from (A2) by substituting in for 
$B$ using (3.5).
While (A3a) robustly estimates the efficiency of the irreversible mixing of the background, vertically varying, stratifying scalar field, there are no measurements of 
$\epsilon _p$ in Conry et al. (Reference Conry, Kit and Fernando2020), so we can only consider the first two sets of definitions. Taking the entries from their table 1 with 
$\varGamma > 0$, we evaluate 
$\varGamma _1$ and 
$\varGamma _r$ and plot them in figure 11. The measurements described by Conry et al. (Reference Conry, Kit and Fernando2020) to be in statistical stationary conditions are labelled using orange stars, and the measurements described to exhibit unsteady effects are labelled using grey triangles. The remaining measurements are shown using black circles. We note that most of the measurements do not lie on the dashed one-to-one line, which we interpret to be due to assumptions that were invoked to estimate the right-hand side quantities in (3.4) and (3.5), but more importantly due to the flow conditions not being statistically stationary and homogeneous. Conry et al. (Reference Conry, Kit and Fernando2020) used 
$\varGamma _r$ in their work, and we have also chosen to use this definition in our work given that it is more directly related to the Osborn eddy diffusivity model for the buoyancy flux 
$D_T \approx B/N^2 \approx \varGamma _r \epsilon _k/N^2$ (Osborn Reference Osborn1980).
Figure 11. Comparison plot of the two definitions of 
$\varGamma$ evaluated using (A1b) and (A2b) from measurements analysed by Conry et al. (Reference Conry, Kit and Fernando2020). Orange stars represent data from statistically stationary conditions, and grey downward-facing triangles represent data from unsteady conditions as labelled by Conry et al. (Reference Conry, Kit and Fernando2020). Black circles represent all other measurements. Most of the data points do not lie on the one-to-one line (dashed line), which we interpret as the consequence of more complex physics than what is captured in (3.4) and (3.5) as well as assumptions that were invoked to estimate 
$P_k$, 
$B$, and 
$\epsilon _k$.
Open access
